基于K-Means聚类与Ridge回归算法的煤炭发热量预测研究

doi:10.12096/j.2096-4528.pgt.23005

基于K-Means聚类与Ridge回归算法的煤炭发热量预测研究

乔世超, 陈衡, 李博, 潘佩媛, 徐钢

热电生产过程污染物监测与控制北京市重点实验室(华北电力大学)，北京市昌平区 102206

Research on Coal Calorific Value Prediction Based on K-Means Clustering and Ridge Regression Algorithm

QIAO Shichao, CHEN Heng, LI Bo, PAN Peiyuan, XU Gang

Beijing Key Laboratory of Emission Surveillance and Control for Thermal Power Generation (North China Electric Power University), Changping District, Beijing 102206, China

收稿日期: 2023-11-15 修回日期: 2024-03-09

基金资助:

国家自然科学基金青年项目. 52106008
国家自然科学基金创新研究群体项目. 51821004

Received: 2023-11-15 Revised: 2024-03-09

作者简介 About authors

乔世超(2000)，男，硕士研究生，研究方向为电站大数据优化，Gregory_Qiao@outlook.com；

陈衡(1989)，男，博士，副教授，研究方向为热力系统优化，本文通信作者，heng@ncepu.edu.cn。

摘要

目的煤炭发热量是衡量煤质的重要评价标准之一，也是动力用煤计价的主要依据。为了能够在降低预测成本的前提下实现对煤炭发热量的高精度快速预测，提出了一种新的预测方法。方法采用K-Means聚类算法对相似煤种进行聚类，样本数据来源于山东某电厂自备煤场近6年的4 269条入场化验信息。在聚类的基础上，分别建立工业分析数据低位发热量的Ridge回归模型，以此作为煤炭发热量的预测模型。结果所建立的K-Means聚类与Ridge回归混合模型在预测效果上表现出色。与传统的多元线性回归模型相比，该混合模型可将平均绝对值误差最高减少30.525%，均方根误差最高降低60.054%，相关系数最高提高2.320%。结论 K-Means聚类与Ridge回归混合模型不仅降低了煤炭发热量的预测成本，还提高了预测的精度和速度，为煤炭发热量的预测提供了一种新思路。

关键词： 燃煤电厂 ; 煤炭发热量 ; 工业分析 ; 预测 ; K-Means聚类 ; Ridge回归

Abstract

Objectives The calorific value of coal is one of the important evaluation criteria for measuring coal quality, and is also the main basis for valuation of power coal. In order to realize high-precision and rapid prediction of coal calorific value while reducing prediction costs, a new prediction method is proposed. Methods The K-Means clustering algorithm is used to cluster similar coal types. The sample data comes from 4 269 entry testing information from a self-contained coal yard of a power plant in Shandong in the past 6 years. On the basis of clustering, Ridge regression models are established from industrial analysis data to received base calorific value, which is used as a prediction model for coal calorific value. Results The established K-Means clustering and Ridge regression hybrid model exhibits excellent prediction performance. Compared with the traditional multiple linear regression model, this hybrid model can reduce the mean absolute error by up to 30.525%, reduce the root mean square error by up to 60.054%, and increase the correlation coefficient by up to 2.320%. Conclusions The mixed model of K-Means clustering and Ridge regression reduces the prediction cost of coal calorific value, and also improves the accuracy and speed of prediction, providing a new idea for predicting coal calorific value.

Keywords： coal-fired power plants ; calorific value of coal ; proximate analysis ; prediction ; K-Means clustering ; Ridge regression

PDF (9159KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

乔世超, 陈衡, 李博, 潘佩媛, 徐钢. 基于K-Means聚类与Ridge回归算法的煤炭发热量预测研究. 发电技术[J], 2025, 46(1): 135-144 DOI:10.12096/j.2096-4528.pgt.23005

QIAO Shichao, CHEN Heng, LI Bo, PAN Peiyuan, XU Gang. Research on Coal Calorific Value Prediction Based on K-Means Clustering and Ridge Regression Algorithm. Power Generation Technology[J], 2025, 46(1): 135-144 DOI:10.12096/j.2096-4528.pgt.23005

0 引言

2021年，我国煤炭消费量占能源消费总量的56.0%^[1]，鉴于我国富煤、贫油、少气的能源结构，我国以煤炭为主体的能源消费结构在短时间内不会改变^[2-4]。随着碳达峰、碳中和目标的提出，促进能源行业向清洁化、低碳化演进已经成为迫切需要解决的问题。综合考虑政策倾向以及我国独特的能源资源禀赋，对传统能源进行技术优化是解决能源行业有序转型问题最经济高效的路径^[5]。因此，对煤炭特性的分析与研究对我国能源行业的发展具有重要意义。

发热量反映了单位质量煤炭完全燃烧时所能释放的能量，是衡量煤炭品质的重要指标，也是动力用煤计价的主要依据。因此，对于发热量的高效准确测量成为了重要的研究课题。

目前，一般采用实验的方法来测定煤的发热量，包括氧弹热量计法、恒温式热量计法、绝热式热量计法等^[6-8]。但由于需要经过严格的程序和专业技术人员的操作，测量周期较长^[9]，这就导致测试结果有一定滞后性。近年来，用于煤炭发热量快速测定的瞬发伽马中子活化分析已在实际生产中小范围应用^[10]，但这种测试方法存在辐射危害、设备昂贵、运行维护成本高等问题^[11]。

随着计算机技术的发展，许多学者利用机器学习算法对燃煤参数与发热量之间的关系进行了研究，建立了一系列发热量预测模型。谭鹏等^[12]建立了非线性支持向量机的煤质发热量预测模型，研究表明，该预测模型比线性模型具备更精准的预测能力。焦发存等^[13]建立了基于灰分和固定碳含量的发热量预测模型，以实现对淮南矿区煤炭发热量的快速估算。李大虎等^[14]采用最大信息系数特征变量选择与粒子群优化-BP神经网络相结合方法，实现了煤炭发热量非线性预测，总体预测效果较优。

鉴于煤的全元素分析需要专业设备、耗时较长、成本较高^[15]，因此多数煤场一般只进行煤的工业分析和硫元素、氢元素分析^[16]，这给发热量的预测造成了一定程度的阻碍。煤炭工业分析具有操作简单、成本低廉、响应时间快的特点，本文依据煤种的工业分析数据，利用K-Means聚类算法对全部批次煤炭进行分类，并采用多元线性回归算法，对性质相似的煤种分别建立发热量关于工业分析数据的预测模型，实现对发热量更高精度的预测。

1 煤样情况

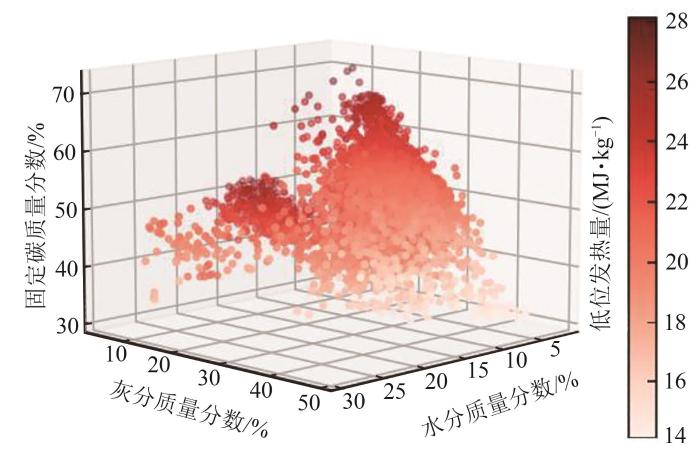
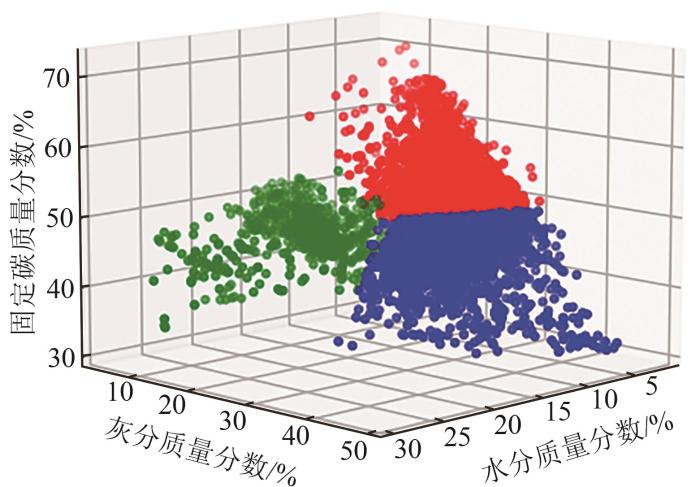
本文以我国北方某电厂自备煤场为研究对象，该煤场燃煤主要来自太原、阳泉、寿阳、榆林等地。煤场内化学实验室每天对不同批次来煤进行化验，并将化验结果录入到SQL Server数据库中。本文选取近6年的4 269条入场化验信息作为样本，建立工业分析与煤炭发热量的多元线性回归模型。由于工业分析中4个参数总和为100%，所以仅需选取其中3个参数作为输入变量。有研究^[17-18]表明，挥发分含量对发热量影响相对较小，且我国锅炉计算一般采用低位发热量作为衡量指标^[19]，故本文选取收到基水分质量分数M_ar、收到基灰分质量分数A_ar以及收到基固定碳质量分数F_C,ar作为输入变量，收到基低位发热量Q_net,ar作为输出变量。经统计，数据集基本情况如表1所示，全部样本数据的分布情况如图1所示。

表1 数据集基本情况

Tab. 1 Basic information of the dataset

参数	最小值	最大值	平均值
收到基低位发热量Q_net，ar/(MJ⋅kg^-1)	14.14	28.18	21.13
收到基水分质量分数M_ar/%	2.15	29.09	9.55
收到基灰分质量分数A_ar/%	4.41	48.52	24.96
收到基固定碳质量分数F_C，ar/%	31.46	71.03	47.08

新窗口打开| 下载CSV

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 样本数据的分布情况

Fig. 1 Distribution of the sample data

2 K-Means聚类算法

2.1 数据归一化

在K-Means聚类算法中，需要采用数据归一化方法减小数据中较大和较小的初始数据所占距离比重对聚类效果的影响，提高模型的收敛速度和计算精度^[20]。数据归一化是将数据按比例缩放，针对一个数据维度中全部数据范围缩放至[0,1]的操作。由此可以降低由于数据的量纲不同或量级差距大对模型的不良影响。本文采用最大-最小值归一化算法，对数据进行归一化处理，用公式表示其原理如下：

x^{'} = \frac{x - x_{m i n}}{x_{m a x} - x_{m i n}}

(1)

式中： $x^{'}$ 为归一化后数据；x为归一化前原始数据；x_max为数据最大值；x_min为数据最小值。

K-Means算法是一种源于信号处理的向量量化方法，现在则更多地用在聚类分析中，并广泛应用于数据挖掘领域^[21]，是一种经典的分割式分群聚类算法。该算法主要目标是将样本中N个点按照相似度聚集到k个聚簇当中，将每个点都分配到离他最近的均值(即聚类中心)对应的聚簇，以之作为聚类的标准。最终，簇内相似度高，簇间相似度低，从而完成聚类。

K-Means算法采用了迭代优化的思想，通常被称为劳埃德算法^[22]。该算法可分为4个步骤：

1）选择初始质心。已知共有n条数据，每个元素都是d维向量，全部数据集合为X，确定聚类簇数k，将全部数据随机分为k个集合，故有X=X₁∪X₂∪…∪X_k，每个集合内元素个数为N_i，并从每个子集中随机选择一个初始聚类中心m=(m₁, m₂, …, m_k )。

2）初始化完成后，将每个样本观测值 $x$ 分配到其最近的集群，并计算出每个观测值到聚类中心m_i 的欧氏距离平方和，将该值命名为组内平方和(within-cluster sum of squares，WCSS)，其表达式为

W_{C S S} = \sum_{i = 1}^{k} \sum_{x \in X_{i}}^{} {‖x - m_{i}‖}^{2}

(2)

3）对先前各个聚簇内所有样本分别取平均值，将其设定为新的质心m_i^*，质心公式为

{m_{i}}^{*} = \frac{1}{N_{i}} \sum_{x \in X_{1}} x

(3)

4）计算旧质心和新质心之间的欧氏距离。算法重复最后2个步骤，直到分配方案不再改变，此时可认为算法达到收敛，组内平方和不再减小，质心不再显著移动，数值上表现为最新一次迭代所获得的质心与上一次迭代所获得的质心间的欧氏距离小于给定阈值。

2.2 最佳聚类数的选取方法

K-Means算法是一种非监督学习算法^[23]，聚类不需要对数据进行训练和学习，而是人为规定聚类数，再通过聚类分析将数据聚合成几个群体。不同的聚类数对最终聚类效果有很大的影响，所以需要采用评价指标辅助确定最佳聚类数，以下是评价聚类效果的3种常用方法。

2.2.1 手肘法

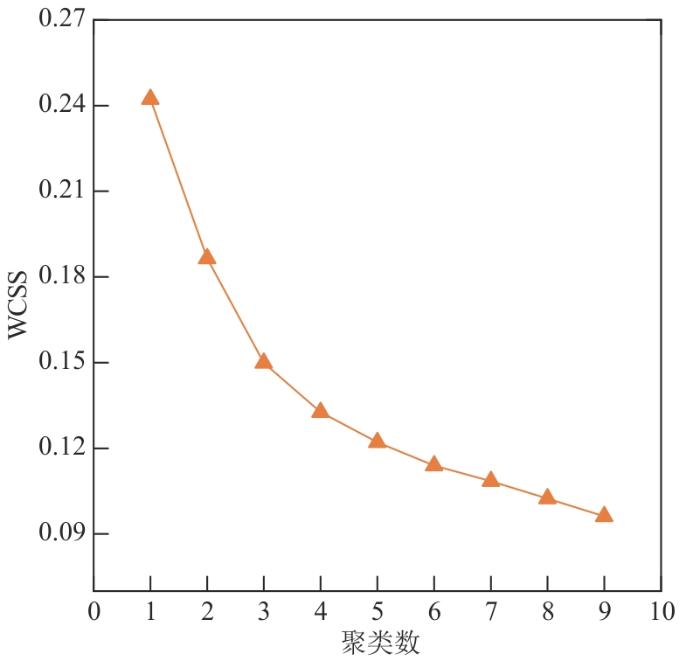
在聚类分析中，手肘法是一种用于确定数据集中聚类数量的方法，由美国心理测量学家罗伯特⋅拉德⋅桑代克于1953年首次提出^[24]，其原理是：设定聚类范围，随着聚类簇数k的增大，样本划分会更加细致，每个簇的聚合程度会逐渐提高，那么WCSS自然会逐渐变小。当k值小于最佳聚类簇数时，k值的不断增大会使每个簇的聚合程度大幅度增加，故WCSS的下降幅度会很大。当k到达最佳聚类数时，再增加k所得到的聚合程度会迅速变小，组内平方和的数值变化也趋于平缓。WCSS与k的关系图是近似于手肘的形状，而这个肘部对应的k值就是数据的最佳聚类数^[25]。

图2是不同聚类数对应的WCSS值，在聚类数k为3时，该点的斜率变化率(前后2段折线斜率比值)最大，此时WCSS值变化最为剧烈，因此将模型聚类数设定为3最为合理。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 手肘法判断最佳聚类数

Fig. 2 Elbow method to determine the optimal number of clustering

2.2.2 轮廓系数法

在机器学习与数据挖掘领域，轮廓系数法是一种反映数据聚类结果一致性的方法，可以用于评估聚类后簇与簇之间的离散程度^[26]。

对于某一个属于簇C_i 的样本i，记为i∈C_i，设d(i, j)为样本i与j之间的欧式距离，并求算样本i与簇内其他样本之间的平均距离，将其命名为凝聚度，记为a(i)，它反映了样本i当前聚类结果的优劣，公式定义如下：

a (i) = \frac{1}{|C_{i}| - 1} \sum_{j \in C_{i}, i \neq j} d (i, j)

(4)

然后定义样本i与其他簇C_k 全部样本之间的平均距离，将最小平均距离命名为分离度，记作b(i)：

b (i) = \underset{_{k \neq i}}{m i n} \frac{1}{|C_{k}|} \sum_{j \in C_{k}} d (i, j)

(5)

综合式(1)—(5)，定义样本i的轮廓系数公式为

s (i) = \frac{b (i) - a (i)}{m a x {a (i), b (i)}}

(6)

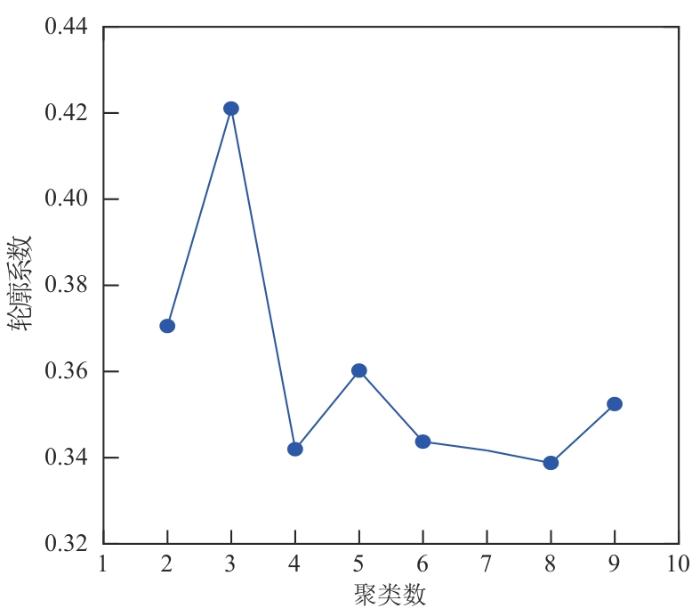
当轮廓系数达到最大值时，可认为对应k值为最佳聚类数。图3为不同聚类数对应的轮廓系数值，当k值为3时，轮廓系数取值最大，对于本研究数据情况，将模型聚类数设定为3最为合理。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 轮廓系数法判断最佳聚类数

Fig. 3 Silhouette coefficient method to determine the optimal number of clustering

2.2.3 卡林斯基-哈拉巴斯指数法

卡林斯基-哈拉巴斯(Calinski-Harabasz，CH)指数是由Calinski和Harabasz于1974年引入的一种可用于在非监督学习中评估聚类模型的指标^[27]。CH指数(也称为方差比标准)通过计算所有集群的集群间离散度总和与集群内离散度总和的比率来对聚类效果进行评价，其定义如下：

C_{H} (k) = \frac{T_{r} (B_{k})}{T_{r} (W_{k})} \times \frac{N - k}{k - 1}

(7)

W_{k} = \sum_{i = 1}^{k} \sum_{x \in X_{i}} (x - m_{i}) (x - m_{i})^{T}

(8)

B_{k} = \sum_{i}^{k} n_{i} (m_{i} - m_{0}) (m_{i} - m_{0})^{T}

(9)

式中： B_k 为组间色散矩阵，计算的是组间协方差； W_k 为群内色散矩阵，计算的是组内协方差；N为全部样本数；n_i 表示i类中的样本数； m₀表示数据集的中心点。

当CH指数达到最大时，说明模型用尽量少的类别聚类了尽可能多的样本，因此聚类效果最优，与之对应的簇数即为最佳聚类数。

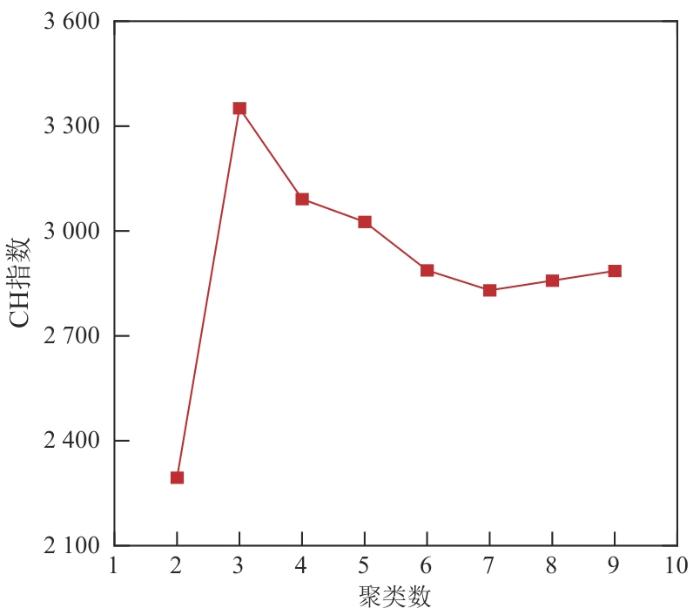
图4是不同聚类数对应的CH指数值，在k值为3时，CH指数值最大，因此针对本研究，将模型聚类数设定为3最为合理。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 卡林斯基-哈拉巴斯系数法判断最佳聚类数

Fig. 4 Calinski-Harabasz index method to determine the optimal number of clustering

2.3 K-Means聚类模型的构建

根据2.2节研究，可以确定最佳聚类数k为3。入场煤M_ar、A_ar以及F_C,ar经过归一化后，利用K-Means算法进行聚类分析。将聚类结果利用Python中Axes3D模块绘制出三维图像，最终聚类结果如图5所示。根据聚类结果图像，可将红色簇内的煤种命名为高固定碳煤，蓝色簇内的煤种命名为高灰分煤，绿色簇内的煤种命名为高水分煤。3类煤的参数范围如表2所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 入场煤聚类结果

Fig. 5 Clustering results for the coal entered the yard

表2 煤种参数范围 (%)

Tab. 2 Range of coal type parameters

煤种	M_ar	A_ar	F_C，ar
高固定碳煤	2.12~15.90	11.94~33.91	46.99~71.03
高灰分煤	3.63~19.51	18.14~48.52	31.46~49.76
高水分煤	9.12~29.03	4.40~23.58	34.17~54.95

新窗口打开| 下载CSV

3 多元线性回归模型

3.1 基本原理

回归是监督学习的一个典型问题，可以用于预测输入变量和输出变量之间的关系^[28]。输出变量的值随输入变量值的变化而变化，回归模型正是表示从输入变量到输出变量映射的函数。

在统计学中，线性回归是利用线性回归方程的最小平方函数对一个或多个自变量(输入变量)和因变量(输出变量)之间关系进行建模的一种回归分析^[29]。其中，大于一个自变量情况的叫作多元线性回归分析^[30]，其基本原理如下：

对于一个有n个输入变量的样本i而言，回归目标函数为

y_{i} = ω_{0} + ω_{1} x_{i 1} + ω_{2} x_{i 2} + \dots + ω_{n} x_{i n} + ε

(10)

式中：ω₀为模型的截距；ω₁—ω_n 为模型的回归系数；ε为随机误差；y_i 为样本i的目标变量；x_i₁—x_in 为样本i上的不同特征。

考虑到一个数学模型有m个样本，回归结果可以表示为

\{\begin{array}{l} y_{1} = ω_{0} + ω_{1} x_{11} + ω_{2} x_{12} + \dots + ω_{n} x_{1 n} + ε_{1} \\ y_{2} = ω_{0} + ω_{1} x_{21} + ω_{2} x_{22} + \dots + ω_{n} x_{2 n} + ε_{2} \\ ⋮ \\ y_{m} = ω_{0} + ω_{1} x_{m 1} + ω_{2} x_{m 2} + \dots + ω_{n} x_{m n} + ε_{m} \end{array}

(11)

则该回归模型可用矩阵表示为

Y = [\begin{matrix} 1 & x_{11} & \dots & x_{1 n} \\ 1 & x_{21} & \dots & x_{2 n} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ 1 & x_{m 1} & \dots & x_{m n} \end{matrix}] [\begin{matrix} ω_{0} \\ ω_{1} \\ ⋮ \\ ω_{n} \end{matrix}] + [\begin{matrix} ε_{1} \\ ε_{2} \\ ⋮ \\ ε_{m} \end{matrix}]

(12)

即

Y = X ω + ε

(13)

式中： Y 是包含m个全部样本回归结果的列向量； X 为变量矩阵； ω 为截距矩阵； ε 为误差矩阵。

3.2 多元线性回归算法

3.2.1 最小二乘法回归算法

最小二乘法(ordinary least squares，OLS)回归是最常见的，也是最简单的回归分析方法。相关回归分析、方差分析和线性模型理论等数理统计学的几大分支都以最小二乘法为理论基础^[31]。其基本原则是使所有残差平方和，即样本点与到线性模型超平面的欧氏距离平方和最小。故定义残差平方和为代价函数C(ω)，其表达式为

C (ω) = \sum_{i = 1}^{n} (y_{i} - ω_{0} - ω_{1} x_{i 1} - \dots - ω_{n} x_{i n})^{2}

(14)

最小二乘法多元线性回归的任务，就是找到参数ω的估计值，使得残差平方和达到最小。根据多元函数求极值原理，在估计值处的代价函数关于回归系数的偏导数应等于0：

\frac{\partial C (ω)}{\partial ω_{}} |_{ω = {\hat{ω}}_{}} = 0

(15)

当( X^TX )^-1存在时，回归参数的最小二乘估计为

\hat{ω} = (X^{T} {X)}^{- 1} X^{T} Y

(16)

由此即可得到要求解的回归方程：

\hat{y} = {\hat{ω}}_{0} + {\hat{ω}}_{1} x_{1} + {\hat{ω}}_{2} x_{2} + \dots + {\hat{ω}}_{n} x_{n}

(17)

3.2.2 OLS回归算法改进

在处理较为复杂数据的回归问题时，OLS线性回归算法通常会出现预测精度不够的问题，导致解得的模型与实际偏差较大。因此，引入复杂度惩罚因子，通过正则项来约束需要优化的参数，从而实现避免过拟合的目的。常用的正则项可以使用L1范数、L2范数或将二者结合，3种方法对应的算法分别为Lasso回归，Ridge回归和Elastic Net回归^[32]，其代价函数分别为：

C_{1} (ω) = \sum_{i = 1}^{n} (y_{i} - ω_{0} - ω_{1} x_{i 1} - \dots - ω_{n} x_{i n})^{2} + λ {‖ω‖}_{1}

(18)

C_{2} (ω) = \sum_{i = 1}^{n} (y_{i} - ω_{0} - ω_{1} x_{i 1} - \dots - ω_{n} x_{i n})^{2} + λ {‖ω‖}_{2}^{2}

(19)

C_{3} (ω) = \sum_{i = 1}^{n} (y_{i} - ω_{0} - ω_{1} x_{i 1} - \dots - ω_{n} x_{i n})^{2} +

λ ρ {‖ω‖}_{1} + \frac{λ (1 - ρ)}{2} {‖ω‖}_{2}^{2}

(20)

式中λ、ρ表示惩罚系数。

3.3 回归模型建立

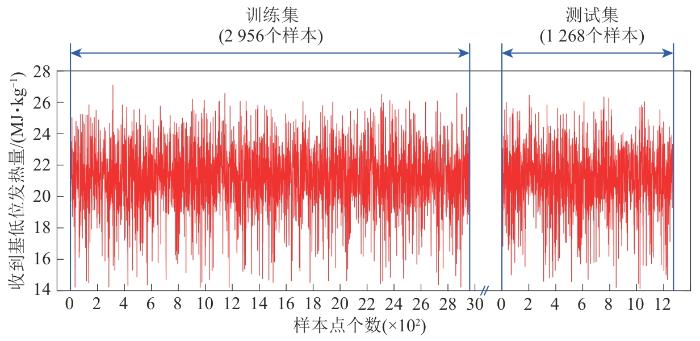
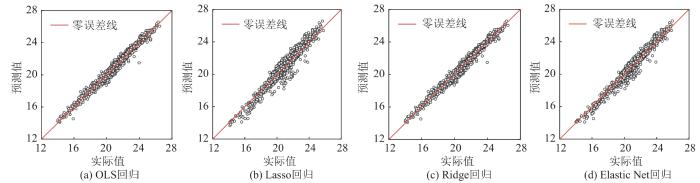
以4 269条数据作为样本，随机选取其中70%的样本作为训练集进行回归拟合，其余的30%作为测试集验证模型准确度，数据集划分情况如图6所示。然后分别利用OLS回归算法、Lasso回归算法、Ridge回归算法和Elastic Net回归算法对训练集数据进行建模，并在测试集中进行验证。图7为预测值与实际值的对比图。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 数据集的划分

Fig. 6 Division of the data set

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 发热量实际值与预测值对比

Fig. 7 Comparison between the predicted heat value and actual heat value

为了使对模型泛化能力的评价更加直观可信，本文引入几个常用的统计学评价指标，对不同回归算法的优劣进行量化评价。

常见的回归算法评估指标有平均绝对值误差 $δ_{M A E}$ 、均方根误差 $δ_{R M S E}$ 、决定系数R²等。其中，误差指标越小，代表预测值与真实值越接近；决定系数能够度量因变量变异中可由自变量解释部分所占的比例，以此来判断回归模型的解释力，决定系数越大，说明模型的解释力越强。上述评价指标对应的公式如下：

δ_{M A E} = \frac{1}{n} \sum_{i = 1}^{n} |{\hat{y}}_{i} - y_{i}|

(21)

δ_{R M S E} = \sqrt[]{\frac{1}{n} \sum_{i = 1}^{n} ({\hat{y}}_{i} - y_{i})^{2}}

(22)

R^{2} = 1 - \frac{\sum_{i = 1}^{n} (y_{i} - {\hat{y}}_{i})^{2}}{\sum_{i = 1}^{n} (y_{i} - {\bar{y}}_{i})^{2}}

(23)

式中： ${\hat{y}}_{i}$ 为预测值； $y_{i}$ 为真实值； ${\bar{y}}_{i}$ 为真实值平均值；n为测试集样本数量。

由此计算出不同方法对应的评价指标数值，回归方程及评价指标结果如表3所示。

表3 不同回归算法对应的模型评价指标

Tab. 3 Model evaluation indicators corresponding to different regression algorithms

回归算法	回归方程	δ_MAE	δ_RMSE	R²
OLS回归	$Q_{n e t, a r} = 26.569 84 - 0.337 03 M_{a r} - 0.291 47 A_{a r} + 0.103 11 F_{C, a r}$	0.270 36	0.628 38	0.942 94
Lasso回归	$Q_{n e t, a r} = 21.542 41 - 0.150 61 M_{a r} - 0.222 05 A_{a r} + 0.133 61 F_{C, a r}$	0.464 60	0.792 84	0.909 16
Ridge回归	$Q_{n e t, a r} = 26.569 15 - 0.337 01 M_{a r} - 0.291 46 A_{a r} + 0.103 12 F_{C, a r}$	0.248 45	0.592 63	0.945 63
Elastic Net回归	$Q_{n e t, a r} = 23.358 12 - 0.220 51 M_{a r} - 0.247 72 A_{a r} + 0.123 42 F_{C, a r}$	0.358 70	0.696 54	0.929 89

新窗口打开| 下载CSV

由表3可以看出，相较于传统的OLS回归模型，Lasso回归模型和Elastic Net回归模型的平均绝对值误差δ_MAE分别增加了71.472%和32.674%，均方根误差δ_RMSE分别增加了26.172%和10.848%，决定系数R²均有一定程度的下降。但采用Ridge回归算法构造回归模型，误差参数有所减小，决定系数也有所提高。

结合图7来看，采用Ridge回归算法的模型，其测试数据关于零误差线分布更加紧密，说明在4种回归算法中，Ridge回归算法预测效果最优。综上所述，从运行结果上来看，采用Ridge回归算法拟合效果更好。

Ridge回归一种以放弃无偏性、降低精度为代价，以解决病态矩阵问题的回归方法，这种方法在自变量高度相关的情况下有更好的拟合效果。统计学中一般采用方差膨胀系数(variance inflation factor，VIF)来衡量多元线性回归模型中多重共线性的严重程度。方差膨胀系数表示回归系数估计量的方差与假设自变量间不线性相关时方差的比值，其表达式如下：

V_{I F} = \frac{1}{1 - R^{2}}

(24)

一般地，当5<VIF<10时，认为模型输入变量有一定多重共线性；当VIF≥10时，认为模型输入变量多重共线性很强。采用Ridge回归模型对M_ar，A_ar以及F_C,ar进行多重共线性分析，结果如表4所示。

表4 输入变量方差膨胀系数

Tab. 4 Variance inflation factors of input variables

输入变量	M_ar	A_ar	F_C，ar
VIF	6.095 27	9.974 05	16.879 13

新窗口打开| 下载CSV

由表4可知，本文研究模型输入变量间多重共线性较强，与Ridge回归算法的使用场景相符。

综上所述，Ridge回归模型的误差较小，决定系数相对较大；且由于模型自变量之间多重共线性较强，Ridge回归在该情况下对回归方程的拟合有更好的表现效果。综合不同回归模型误差结果对比和Ridge回归算法特性理论推导，确定本文选用Ridge回归算法对煤场数据进行构建多元线性回归模型。

4 K-Means聚类-Ridge回归混合模型

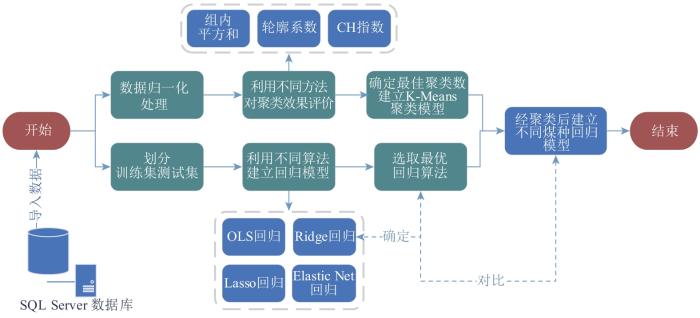
建立K-Means聚类-Ridge回归混合模型，来对分类后的煤种逐一进行回归计算，其流程如图8所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 模型的建立流程

Fig. 8 Process of building model

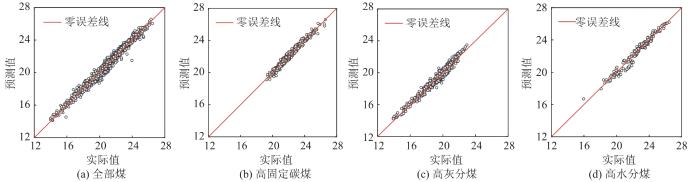
对燃煤数据建立K-Means聚类-Ridge回归混合模型，得到相似煤种各自的回归方程及相关评价指标，如表5所示。不同煤种预测模型的实际值与预测值对比如图9所示。由表5和图9可以看出，聚类后回归效果较聚类前有明显的改善，其中高固定碳煤最为明显，可将平均绝对值误差降低30.525%，均方根误差降低60.054%，决定系数提高2.320%。

表5 K-Means聚类后对应不同煤种的回归模型评价指标

Tab. 5 Model evaluation indicators of regression models corresponding to different coal types after K-Means clustering

煤炭种类	回归方程	δ_MAE	δ_RMSE	R²
全部煤	$Q_{n e t, a r} = 26.569 15 - 0.337 01 M_{a r} - 0.291 46 A_{a r} + 0.103 12 F_{C, a r}$	0.248 45	0.592 63	0.945 63
高固定碳煤	$Q_{n e t, a r} = 28.753 18 - 0.345 87 M_{a r} - 0.315 47 A_{a r} + 0.076 18 F_{C, a r}$	0.172 61	0.236 73	0.967 57
高灰分煤	$Q_{n e t, a r} = 24.843 48 - 0.301 57 M_{a r} - 0.276 01 A_{a r} + 0.125 64 F_{C, a r}$	0.224 37	0.348 47	0.963 36
高水分煤	$Q_{n e t, a r} = 28.329 07 - 0.404 50 M_{a r} - 0.299 58 A_{a r} + 0.089 79 F_{C, a r}$	0.247 84	0.409 61	0.957 69

新窗口打开| 下载CSV

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 聚类后不同煤种发热量实际值与预测值对比

Fig. 9 Comparison between actual calorific value and predicted calorific value of different coal types after clustering

由上述分析可知，采用K-Means聚类-Ridge回归混合模型能在一定程度上提高根据工业分析预测煤炭发热量的准确度，结果与预期效果一致。

5 结论

1）相较几种实测法测定煤炭发热量，采用建立燃煤线性回归模型的方法可以节省大量的人力与物力，并且可以实现煤炭发热量的在线快速预测。

2）由于煤炭的工业分析数据间有很强的多重共线性，因此相较传统的最小二乘法回归方法以及其他改进方法，Ridge回归方法在煤炭工业分析发热量的预测中有更好的准确性和可信度。

3）与未经聚类的全部煤样对应的回归模型相比，经过K-Means聚类后的煤样预测模型的平均绝对值误差δ_MAE和均方根误差δ_RMSE分别最高减少30.525%和60.054%，决定系数R²最高增加2.320%，一定程度上提高了预测的精度。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

国家统计局．

中华人民共和国2021年国民经济和社会发展统计公报

[EB/OL]．(2022-02-16)[2024-03-24]．． doi:10.3969/j.issn.1002-4557.2003.03.003