A review of state of health estimation of energy storage systems:challenges and possible solutions for futuristic applications of Li-ion battery packs in electric vehicles
2
2019
... 锂离子电池具有能量密度高、自放电低、寿命长等优点,已经在很多领域得到应用[1-2].在锂离子电池全球市场规模日益扩大的背景下,荷电状态(state of charge,SOC)估算等相关技术研究也需要逐步完善,以切实保障锂离子电池在多场景下的推广应用.SOC的准确估计对防止电池过充过放、延长电池循环寿命具有重要作用.然而锂离子电池高度非线性且其SOC受多种因素影响,导致难以准确估计SOC.因此,锂离子电池SOC估算方法一直被广泛关注. ...
... 目前,已有部分学者对SOC、SOH、RUL的估计及预测方法进行了梳理与总结[1-5].然而随着电池行业的发展,电池状态估计与寿命预测方法已有大量创新,以往综述并不能全面覆盖创新方法.因此,本文根据近期研究进行了再次梳理与总结,介绍了SOC、SOH及RUL的估计方法,并基于当前研究存在的问题,提出了未来锂离子电池状态估计与RUL预测的研究方向. ...
A technique for estimating the state of health of lithium batteries through a dual-sliding-mode observer
1
2010
... 锂离子电池具有能量密度高、自放电低、寿命长等优点,已经在很多领域得到应用[1-2].在锂离子电池全球市场规模日益扩大的背景下,荷电状态(state of charge,SOC)估算等相关技术研究也需要逐步完善,以切实保障锂离子电池在多场景下的推广应用.SOC的准确估计对防止电池过充过放、延长电池循环寿命具有重要作用.然而锂离子电池高度非线性且其SOC受多种因素影响,导致难以准确估计SOC.因此,锂离子电池SOC估算方法一直被广泛关注. ...
Comparison of prognostic algorithms for estimating remaining useful life of batterie
1
2009
... 另外,在锂离子电池的连续充放电过程中,电池性能会随着容量降低和阻抗增加而恶化,易出现内短路、热失控等问题,导致设备和系统故障,甚至灾难性事故[3].因此,准确估算电池健康度(state of health,SOH)与预测剩余寿命(remaining useful life,RUL)以提升电池的可靠性也非常关键[4]. ...
Review of hybrid prognostics approaches for remaining useful life prediction of engineered systems,and an application to battery life prediction
1
2014
... 另外,在锂离子电池的连续充放电过程中,电池性能会随着容量降低和阻抗增加而恶化,易出现内短路、热失控等问题,导致设备和系统故障,甚至灾难性事故[3].因此,准确估算电池健康度(state of health,SOH)与预测剩余寿命(remaining useful life,RUL)以提升电池的可靠性也非常关键[4]. ...
锂离子电池荷电状态估算方法及其应用场景综述
2
2022
... 目前,已有部分学者对SOC、SOH、RUL的估计及预测方法进行了梳理与总结[1-5].然而随着电池行业的发展,电池状态估计与寿命预测方法已有大量创新,以往综述并不能全面覆盖创新方法.因此,本文根据近期研究进行了再次梳理与总结,介绍了SOC、SOH及RUL的估计方法,并基于当前研究存在的问题,提出了未来锂离子电池状态估计与RUL预测的研究方向. ...
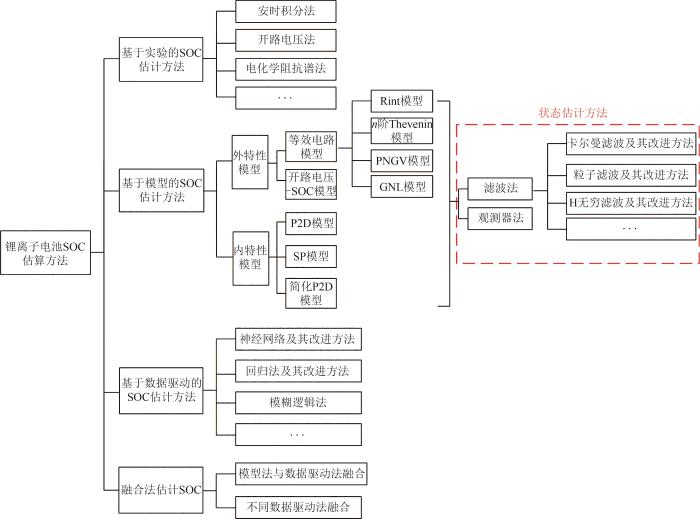
... 本文将锂离子电池SOC估计方法归纳为以下4类[5]: ...
锂离子电池荷电状态估算方法及其应用场景综述
2
2022
... 目前,已有部分学者对SOC、SOH、RUL的估计及预测方法进行了梳理与总结[1-5].然而随着电池行业的发展,电池状态估计与寿命预测方法已有大量创新,以往综述并不能全面覆盖创新方法.因此,本文根据近期研究进行了再次梳理与总结,介绍了SOC、SOH及RUL的估计方法,并基于当前研究存在的问题,提出了未来锂离子电池状态估计与RUL预测的研究方向. ...
... 本文将锂离子电池SOC估计方法归纳为以下4类[5]: ...
一种分阶段锂离子电池荷电状态估计算法
1
2020
... 1)基于实验的SOC估计方法[6].通过实验测量电池表征数值来进行SOC的精确估算. ...
一种分阶段锂离子电池荷电状态估计算法
1
2020
... 1)基于实验的SOC估计方法[6].通过实验测量电池表征数值来进行SOC的精确估算. ...
基于电化学模型的锂离子电池荷电状态估计方法综述
1
2022
... 2)基于模型的SOC估计方法[7-8].通过建立等效电路模型、电化学模型等相关电池模型,估计其状态参数来实现电池SOC的估算. ...
基于电化学模型的锂离子电池荷电状态估计方法综述
1
2022
... 2)基于模型的SOC估计方法[7-8].通过建立等效电路模型、电化学模型等相关电池模型,估计其状态参数来实现电池SOC的估算. ...
基于最大相关熵扩展卡尔曼滤波算法的锂离子电池荷电状态估计
2
2021
... 2)基于模型的SOC估计方法[7-8].通过建立等效电路模型、电化学模型等相关电池模型,估计其状态参数来实现电池SOC的估算. ...
... P2D模型将锂电池等效为由无数球型固相颗粒组成的电极(正极和负极)、隔膜及电解液组成的结构,通过一系列偏微分方程(partial differential equation,PDE)描述电池内部动态机制,可以进行精确的电池状态估计并具有通用性和可扩展性,适用于不同材料体系的电池,可以发展和延伸为更复杂的多场耦合模型.然而对于复杂模型,除了参数过多外,PDE也较难找到解析解[8]. ...
基于最大相关熵扩展卡尔曼滤波算法的锂离子电池荷电状态估计
2
2021
... 2)基于模型的SOC估计方法[7-8].通过建立等效电路模型、电化学模型等相关电池模型,估计其状态参数来实现电池SOC的估算. ...
... P2D模型将锂电池等效为由无数球型固相颗粒组成的电极(正极和负极)、隔膜及电解液组成的结构,通过一系列偏微分方程(partial differential equation,PDE)描述电池内部动态机制,可以进行精确的电池状态估计并具有通用性和可扩展性,适用于不同材料体系的电池,可以发展和延伸为更复杂的多场耦合模型.然而对于复杂模型,除了参数过多外,PDE也较难找到解析解[8]. ...
基于门控循环单元神经网络和Huber-M估计鲁棒卡尔曼滤波融合方法的锂离子电池荷电状态估算方法
1
2020
... 3)基于数据驱动的SOC估计方法[9].通过大量数据拟合并借助数学模型来估算电池SOC. ...
基于门控循环单元神经网络和Huber-M估计鲁棒卡尔曼滤波融合方法的锂离子电池荷电状态估算方法
1
2020
... 3)基于数据驱动的SOC估计方法[9].通过大量数据拟合并借助数学模型来估算电池SOC. ...
融合算法在蓄电池 SOC 估算中的研究综述
1
2021
... 4)基于融合方法的SOC估计方法[10].多类方法取长补短,以达到提升SOC估算精度、降低计算时间的效果. ...
融合算法在蓄电池 SOC 估算中的研究综述
1
2021
... 4)基于融合方法的SOC估计方法[10].多类方法取长补短,以达到提升SOC估算精度、降低计算时间的效果. ...
提高安时积分法估算电池SOC精度的方法比较
1
2010
... 上述误差具有累积效应,因此单纯采用安时积分法很难满足荷电状态估计的精度要求.部分学者对提升安时积分法精度展开了研究.文献[11]对磷酸铁锂动力电池进行测试,比较了各参数对于提高SOC估算精度的重要性,结果表明,初始SOC修正方法对于提高安时积分法的精度最为重要.文献[12]指出安时积分法常采用开环的工作模式,若在仿真过程中未对测试电流进行及时修正,则会导致较大的测量累积误差;同时,针对传统安时积分法因将电池可用容量视为定值而带来的误差,提出了带容量修正的安时积分法.文献[13]针对传统安时积分法由于无法在线更新库仑效率而带来误差的问题,提出一种利用不同库仑效率对分段积分后电量进行修正的安时积分法. ...
提高安时积分法估算电池SOC精度的方法比较
1
2010
... 上述误差具有累积效应,因此单纯采用安时积分法很难满足荷电状态估计的精度要求.部分学者对提升安时积分法精度展开了研究.文献[11]对磷酸铁锂动力电池进行测试,比较了各参数对于提高SOC估算精度的重要性,结果表明,初始SOC修正方法对于提高安时积分法的精度最为重要.文献[12]指出安时积分法常采用开环的工作模式,若在仿真过程中未对测试电流进行及时修正,则会导致较大的测量累积误差;同时,针对传统安时积分法因将电池可用容量视为定值而带来的误差,提出了带容量修正的安时积分法.文献[13]针对传统安时积分法由于无法在线更新库仑效率而带来误差的问题,提出一种利用不同库仑效率对分段积分后电量进行修正的安时积分法. ...
基于容量修正的安时积分SOC估算方法研究
1
2020
... 上述误差具有累积效应,因此单纯采用安时积分法很难满足荷电状态估计的精度要求.部分学者对提升安时积分法精度展开了研究.文献[11]对磷酸铁锂动力电池进行测试,比较了各参数对于提高SOC估算精度的重要性,结果表明,初始SOC修正方法对于提高安时积分法的精度最为重要.文献[12]指出安时积分法常采用开环的工作模式,若在仿真过程中未对测试电流进行及时修正,则会导致较大的测量累积误差;同时,针对传统安时积分法因将电池可用容量视为定值而带来的误差,提出了带容量修正的安时积分法.文献[13]针对传统安时积分法由于无法在线更新库仑效率而带来误差的问题,提出一种利用不同库仑效率对分段积分后电量进行修正的安时积分法. ...
基于容量修正的安时积分SOC估算方法研究
1
2020
... 上述误差具有累积效应,因此单纯采用安时积分法很难满足荷电状态估计的精度要求.部分学者对提升安时积分法精度展开了研究.文献[11]对磷酸铁锂动力电池进行测试,比较了各参数对于提高SOC估算精度的重要性,结果表明,初始SOC修正方法对于提高安时积分法的精度最为重要.文献[12]指出安时积分法常采用开环的工作模式,若在仿真过程中未对测试电流进行及时修正,则会导致较大的测量累积误差;同时,针对传统安时积分法因将电池可用容量视为定值而带来的误差,提出了带容量修正的安时积分法.文献[13]针对传统安时积分法由于无法在线更新库仑效率而带来误差的问题,提出一种利用不同库仑效率对分段积分后电量进行修正的安时积分法. ...
基于频繁项统计的流-安时积分SOC估计方法
1
2022
... 上述误差具有累积效应,因此单纯采用安时积分法很难满足荷电状态估计的精度要求.部分学者对提升安时积分法精度展开了研究.文献[11]对磷酸铁锂动力电池进行测试,比较了各参数对于提高SOC估算精度的重要性,结果表明,初始SOC修正方法对于提高安时积分法的精度最为重要.文献[12]指出安时积分法常采用开环的工作模式,若在仿真过程中未对测试电流进行及时修正,则会导致较大的测量累积误差;同时,针对传统安时积分法因将电池可用容量视为定值而带来的误差,提出了带容量修正的安时积分法.文献[13]针对传统安时积分法由于无法在线更新库仑效率而带来误差的问题,提出一种利用不同库仑效率对分段积分后电量进行修正的安时积分法. ...
基于频繁项统计的流-安时积分SOC估计方法
1
2022
... 上述误差具有累积效应,因此单纯采用安时积分法很难满足荷电状态估计的精度要求.部分学者对提升安时积分法精度展开了研究.文献[11]对磷酸铁锂动力电池进行测试,比较了各参数对于提高SOC估算精度的重要性,结果表明,初始SOC修正方法对于提高安时积分法的精度最为重要.文献[12]指出安时积分法常采用开环的工作模式,若在仿真过程中未对测试电流进行及时修正,则会导致较大的测量累积误差;同时,针对传统安时积分法因将电池可用容量视为定值而带来的误差,提出了带容量修正的安时积分法.文献[13]针对传统安时积分法由于无法在线更新库仑效率而带来误差的问题,提出一种利用不同库仑效率对分段积分后电量进行修正的安时积分法. ...
基于OCV-SOC曲线簇的磷酸铁锂电池SOC估算研究
1
2019
... 由于电池在长时间静置的条件下,其端电压与SOC有固定的函数关系,因此测量开路电压(open circuit voltage,OCV)与SOC的对应图即可获得电池SOC[14].安时积分法在使用时,常在充放电初/末段依靠OCV-SOC曲线进行校准.然而开路电压法存在以下3个问题: ...
基于OCV-SOC曲线簇的磷酸铁锂电池SOC估算研究
1
2019
... 由于电池在长时间静置的条件下,其端电压与SOC有固定的函数关系,因此测量开路电压(open circuit voltage,OCV)与SOC的对应图即可获得电池SOC[14].安时积分法在使用时,常在充放电初/末段依靠OCV-SOC曲线进行校准.然而开路电压法存在以下3个问题: ...
动力锂离子电池荷电状态估计综述
2
2018
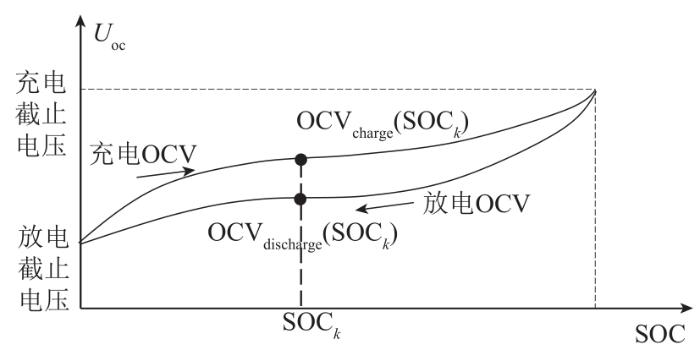
... 3)如图2所示,电池存在迟滞效应[15],同一电压在充电和放电时对应的SOC不同,此特点也将导致SOC计算产生较大误差. ...
... 电化学阻抗谱法采用小幅度正弦交流信号对电化学电源系统进行微扰,通过测量不同频率下的电池阻抗值,找出与电池SOC变化最相关的电池内部反应机理,以此来估计电池SOC值[15-17].电化学阻抗谱法可快速、直接反映电池动力学特性,可将SOC的影响因素解耦研究,但实际应用中电化学阻抗谱测量较为困难. ...
动力锂离子电池荷电状态估计综述
2
2018
... 3)如图2所示,电池存在迟滞效应[15],同一电压在充电和放电时对应的SOC不同,此特点也将导致SOC计算产生较大误差. ...
... 电化学阻抗谱法采用小幅度正弦交流信号对电化学电源系统进行微扰,通过测量不同频率下的电池阻抗值,找出与电池SOC变化最相关的电池内部反应机理,以此来估计电池SOC值[15-17].电化学阻抗谱法可快速、直接反映电池动力学特性,可将SOC的影响因素解耦研究,但实际应用中电化学阻抗谱测量较为困难. ...
Impedance measurements on lead-acid batteries for state-of-charge,state-of-health and cranking capability prognosis in electric and hybrid electric vehicles
0
2005
Impedance measurements combined with the fuzzy logic methodology to assess the SOC and SOH of lithium-ion cells
1
2010
... 电化学阻抗谱法采用小幅度正弦交流信号对电化学电源系统进行微扰,通过测量不同频率下的电池阻抗值,找出与电池SOC变化最相关的电池内部反应机理,以此来估计电池SOC值[15-17].电化学阻抗谱法可快速、直接反映电池动力学特性,可将SOC的影响因素解耦研究,但实际应用中电化学阻抗谱测量较为困难. ...
电动汽车动力电池荷电状态估计方法探讨
1
2014
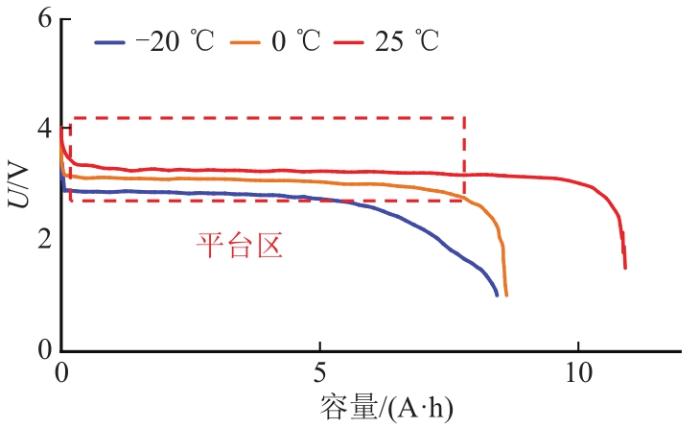
... 负载电压法也是常用的SOC估算方法.由于负载电压随SOC变化的规律与开路电压随SOC变化的规律相似,因此可以根据电压变化大致计算SOC[18].此方法具有操作简单、估算效率高等优点.但由于锂电池端电压与SOC之间的关系曲线存在“平台区”[19],如图3所示,平台区某一开路电压对应容量范围较广,在此区间内端电压估算不准确将导致较大的SOC估算误差.另外,电流工况变化大时,由于极化电压的存在,电池端电压与开路电压变化规律偏差较大,也将给SOC计算带来误差. ...
电动汽车动力电池荷电状态估计方法探讨
1
2014
... 负载电压法也是常用的SOC估算方法.由于负载电压随SOC变化的规律与开路电压随SOC变化的规律相似,因此可以根据电压变化大致计算SOC[18].此方法具有操作简单、估算效率高等优点.但由于锂电池端电压与SOC之间的关系曲线存在“平台区”[19],如图3所示,平台区某一开路电压对应容量范围较广,在此区间内端电压估算不准确将导致较大的SOC估算误差.另外,电流工况变化大时,由于极化电压的存在,电池端电压与开路电压变化规律偏差较大,也将给SOC计算带来误差. ...
基于智能代理分布式管理系统的电动汽车充放电策略
1
2021
... 负载电压法也是常用的SOC估算方法.由于负载电压随SOC变化的规律与开路电压随SOC变化的规律相似,因此可以根据电压变化大致计算SOC[18].此方法具有操作简单、估算效率高等优点.但由于锂电池端电压与SOC之间的关系曲线存在“平台区”[19],如图3所示,平台区某一开路电压对应容量范围较广,在此区间内端电压估算不准确将导致较大的SOC估算误差.另外,电流工况变化大时,由于极化电压的存在,电池端电压与开路电压变化规律偏差较大,也将给SOC计算带来误差. ...
基于智能代理分布式管理系统的电动汽车充放电策略
1
2021
... 负载电压法也是常用的SOC估算方法.由于负载电压随SOC变化的规律与开路电压随SOC变化的规律相似,因此可以根据电压变化大致计算SOC[18].此方法具有操作简单、估算效率高等优点.但由于锂电池端电压与SOC之间的关系曲线存在“平台区”[19],如图3所示,平台区某一开路电压对应容量范围较广,在此区间内端电压估算不准确将导致较大的SOC估算误差.另外,电流工况变化大时,由于极化电压的存在,电池端电压与开路电压变化规律偏差较大,也将给SOC计算带来误差. ...
锂离子电池建模现状综述
3
2022
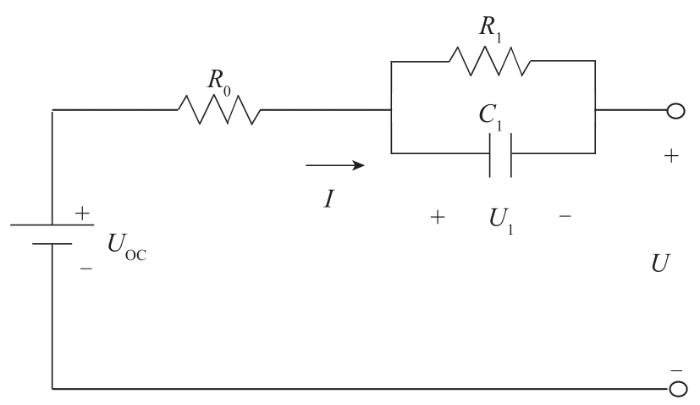
... 基于外特性模型的SOC估算方法较为简单,计算量小,工程应用较为容易.外特性模型包括等效电路模型与开路电压-SOC模型.常用的等效电路模型有Rint模型、PNGV模型[20]、n阶Thevenin模型[20-21](n阶RC模型)、GNL模型[20]等.各等效电路模型对比如表1所示. ...
... [20-21](n阶RC模型)、GNL模型[20]等.各等效电路模型对比如表1所示. ...
... [20]等.各等效电路模型对比如表1所示. ...
锂离子电池建模现状综述
3
2022
... 基于外特性模型的SOC估算方法较为简单,计算量小,工程应用较为容易.外特性模型包括等效电路模型与开路电压-SOC模型.常用的等效电路模型有Rint模型、PNGV模型[20]、n阶Thevenin模型[20-21](n阶RC模型)、GNL模型[20]等.各等效电路模型对比如表1所示. ...
... [20-21](n阶RC模型)、GNL模型[20]等.各等效电路模型对比如表1所示. ...
... [20]等.各等效电路模型对比如表1所示. ...
锂电池二阶RC等效电路模型参数辨识
1
2020
... 基于外特性模型的SOC估算方法较为简单,计算量小,工程应用较为容易.外特性模型包括等效电路模型与开路电压-SOC模型.常用的等效电路模型有Rint模型、PNGV模型[20]、n阶Thevenin模型[20-21](n阶RC模型)、GNL模型[20]等.各等效电路模型对比如表1所示. ...
锂电池二阶RC等效电路模型参数辨识
1
2020
... 基于外特性模型的SOC估算方法较为简单,计算量小,工程应用较为容易.外特性模型包括等效电路模型与开路电压-SOC模型.常用的等效电路模型有Rint模型、PNGV模型[20]、n阶Thevenin模型[20-21](n阶RC模型)、GNL模型[20]等.各等效电路模型对比如表1所示. ...
Power conditioning system for a grid connected PV power generation using a Quasi-Z-source inverter
1
2010
... 基于开路电压-SOC模型的估算方法也可估算锂离子电池SOC.目前,主要模型[22]有Shepherd模型(式(3))、Unnewehr universal模型(式(4))、Nernst模型(式(5))及复合模型(式(6)): ...
基于卡尔曼滤波修正算法的电池SOC估算
1
2014
... KF可以利用输出数据不断对系统状态变量进行修正,并给出状态量下一时刻的最优估计[23].KF能够较好地抵抗噪声干扰并对初始值依赖较低,因此被广泛用于电池SOC研究. ...
基于卡尔曼滤波修正算法的电池SOC估算
1
2014
... KF可以利用输出数据不断对系统状态变量进行修正,并给出状态量下一时刻的最优估计[23].KF能够较好地抵抗噪声干扰并对初始值依赖较低,因此被广泛用于电池SOC研究. ...
考虑环境温度影响的锂离子电池改进双极化模型及其荷电状态估算
1
2021
... 由于锂离子电池为非线性系统,因此用扩展卡尔曼滤波(extended Kalman filter,EKF)对SOC进行估算[24],该方法通过在工作点处进行泰勒展开来解决系统非线性带来的问题. ...
考虑环境温度影响的锂离子电池改进双极化模型及其荷电状态估算
1
2021
... 由于锂离子电池为非线性系统,因此用扩展卡尔曼滤波(extended Kalman filter,EKF)对SOC进行估算[24],该方法通过在工作点处进行泰勒展开来解决系统非线性带来的问题. ...
基于无迹卡尔曼滤波的动力锂电池SOC估计与实现
1
2014
... 对于问题3),EKF高度依赖电池模型为其固有弊端,仅能通过提升模型或参数辨识精度解决.目前已有研究主要围绕问题1)、2).针对问题1),有学者使用无迹卡尔曼滤波(unscented Kalman filter,UKF)来估算锂离子电池SOC[25],该方法通过无损变换使非线性系统方程适用于线性假设下的标准卡尔曼体系,消除了EKF中利用非线性函数泰勒展开的一阶偏导部分产生的较大误差.然而,该方法要精确获得系统过程噪声和观测噪声的统计特性.另外,由于其计算过程均为矩阵运算,当系统中存在电压、电流的剧烈波动,或因计算机字长效应会使其矩阵无法保证严格的正定性,导致状态估计发散,估算不稳定[26],运算负担较大.针对UKF不稳定的问题,部分学者提出了平方根无迹卡尔曼滤波(square root unscented Kalman filter,SR-UKF),利用 Cholesky 分解因子更新和矩阵 Q 、 R 分解保证协方差矩阵的半正定性,增加了数字稳定性[27].然而,问题2)依然存在. ...
基于无迹卡尔曼滤波的动力锂电池SOC估计与实现
1
2014
... 对于问题3),EKF高度依赖电池模型为其固有弊端,仅能通过提升模型或参数辨识精度解决.目前已有研究主要围绕问题1)、2).针对问题1),有学者使用无迹卡尔曼滤波(unscented Kalman filter,UKF)来估算锂离子电池SOC[25],该方法通过无损变换使非线性系统方程适用于线性假设下的标准卡尔曼体系,消除了EKF中利用非线性函数泰勒展开的一阶偏导部分产生的较大误差.然而,该方法要精确获得系统过程噪声和观测噪声的统计特性.另外,由于其计算过程均为矩阵运算,当系统中存在电压、电流的剧烈波动,或因计算机字长效应会使其矩阵无法保证严格的正定性,导致状态估计发散,估算不稳定[26],运算负担较大.针对UKF不稳定的问题,部分学者提出了平方根无迹卡尔曼滤波(square root unscented Kalman filter,SR-UKF),利用 Cholesky 分解因子更新和矩阵 Q 、 R 分解保证协方差矩阵的半正定性,增加了数字稳定性[27].然而,问题2)依然存在. ...
基于离散滑模观测器的锂电池荷电状态估计
1
2015
... 对于问题3),EKF高度依赖电池模型为其固有弊端,仅能通过提升模型或参数辨识精度解决.目前已有研究主要围绕问题1)、2).针对问题1),有学者使用无迹卡尔曼滤波(unscented Kalman filter,UKF)来估算锂离子电池SOC[25],该方法通过无损变换使非线性系统方程适用于线性假设下的标准卡尔曼体系,消除了EKF中利用非线性函数泰勒展开的一阶偏导部分产生的较大误差.然而,该方法要精确获得系统过程噪声和观测噪声的统计特性.另外,由于其计算过程均为矩阵运算,当系统中存在电压、电流的剧烈波动,或因计算机字长效应会使其矩阵无法保证严格的正定性,导致状态估计发散,估算不稳定[26],运算负担较大.针对UKF不稳定的问题,部分学者提出了平方根无迹卡尔曼滤波(square root unscented Kalman filter,SR-UKF),利用 Cholesky 分解因子更新和矩阵 Q 、 R 分解保证协方差矩阵的半正定性,增加了数字稳定性[27].然而,问题2)依然存在. ...
基于离散滑模观测器的锂电池荷电状态估计
1
2015
... 对于问题3),EKF高度依赖电池模型为其固有弊端,仅能通过提升模型或参数辨识精度解决.目前已有研究主要围绕问题1)、2).针对问题1),有学者使用无迹卡尔曼滤波(unscented Kalman filter,UKF)来估算锂离子电池SOC[25],该方法通过无损变换使非线性系统方程适用于线性假设下的标准卡尔曼体系,消除了EKF中利用非线性函数泰勒展开的一阶偏导部分产生的较大误差.然而,该方法要精确获得系统过程噪声和观测噪声的统计特性.另外,由于其计算过程均为矩阵运算,当系统中存在电压、电流的剧烈波动,或因计算机字长效应会使其矩阵无法保证严格的正定性,导致状态估计发散,估算不稳定[26],运算负担较大.针对UKF不稳定的问题,部分学者提出了平方根无迹卡尔曼滤波(square root unscented Kalman filter,SR-UKF),利用 Cholesky 分解因子更新和矩阵 Q 、 R 分解保证协方差矩阵的半正定性,增加了数字稳定性[27].然而,问题2)依然存在. ...
基于平方根无迹卡尔曼滤波的锂电池状态估计
1
2017
... 对于问题3),EKF高度依赖电池模型为其固有弊端,仅能通过提升模型或参数辨识精度解决.目前已有研究主要围绕问题1)、2).针对问题1),有学者使用无迹卡尔曼滤波(unscented Kalman filter,UKF)来估算锂离子电池SOC[25],该方法通过无损变换使非线性系统方程适用于线性假设下的标准卡尔曼体系,消除了EKF中利用非线性函数泰勒展开的一阶偏导部分产生的较大误差.然而,该方法要精确获得系统过程噪声和观测噪声的统计特性.另外,由于其计算过程均为矩阵运算,当系统中存在电压、电流的剧烈波动,或因计算机字长效应会使其矩阵无法保证严格的正定性,导致状态估计发散,估算不稳定[26],运算负担较大.针对UKF不稳定的问题,部分学者提出了平方根无迹卡尔曼滤波(square root unscented Kalman filter,SR-UKF),利用 Cholesky 分解因子更新和矩阵 Q 、 R 分解保证协方差矩阵的半正定性,增加了数字稳定性[27].然而,问题2)依然存在. ...
基于平方根无迹卡尔曼滤波的锂电池状态估计
1
2017
... 对于问题3),EKF高度依赖电池模型为其固有弊端,仅能通过提升模型或参数辨识精度解决.目前已有研究主要围绕问题1)、2).针对问题1),有学者使用无迹卡尔曼滤波(unscented Kalman filter,UKF)来估算锂离子电池SOC[25],该方法通过无损变换使非线性系统方程适用于线性假设下的标准卡尔曼体系,消除了EKF中利用非线性函数泰勒展开的一阶偏导部分产生的较大误差.然而,该方法要精确获得系统过程噪声和观测噪声的统计特性.另外,由于其计算过程均为矩阵运算,当系统中存在电压、电流的剧烈波动,或因计算机字长效应会使其矩阵无法保证严格的正定性,导致状态估计发散,估算不稳定[26],运算负担较大.针对UKF不稳定的问题,部分学者提出了平方根无迹卡尔曼滤波(square root unscented Kalman filter,SR-UKF),利用 Cholesky 分解因子更新和矩阵 Q 、 R 分解保证协方差矩阵的半正定性,增加了数字稳定性[27].然而,问题2)依然存在. ...
基于自适应卡尔曼滤波的锂离子电池SOC估计
1
2011
... 针对问题2),文献[28]提出了自适应扩展卡尔曼滤波(adaptive extended Kalman filter,AEKF)法,AEKF在EKF的基础上,针对协方差矩阵 Q 和 R 不可知导致滤波发散的问题,在EKF的基本原理中添加一个遗忘因子,通过观测值修正误差的协方差,通过动态变化 Q 和 R 提高其收敛速度.然而,AEKF未考虑到模型及方程参数变化,遗忘因子固定也会带来误差. ...
基于自适应卡尔曼滤波的锂离子电池SOC估计
1
2011
... 针对问题2),文献[28]提出了自适应扩展卡尔曼滤波(adaptive extended Kalman filter,AEKF)法,AEKF在EKF的基础上,针对协方差矩阵 Q 和 R 不可知导致滤波发散的问题,在EKF的基本原理中添加一个遗忘因子,通过观测值修正误差的协方差,通过动态变化 Q 和 R 提高其收敛速度.然而,AEKF未考虑到模型及方程参数变化,遗忘因子固定也会带来误差. ...
Particle filter for state of charge and state of health estimation forlithium-iron phosphate batteries
1
2013
... PF的思想基于蒙特卡洛方法,利用粒子集来表示概率,可以用在任何形式的状态空间模型上.相比于KF,PF不对系统做线性假设和后验概率的高斯假设,是一种非线性、非高斯的滤波方法.文献[29]使用PF进行磷酸铁锂离子电池SOC估算,结果显示,其能较好地描述非线性系统的外部特性,显著提升SOC的预测精度,然而容易出现粒子退化问题.文献[30]为解决粒子匮乏、噪声扰动等问题,提出一种改进的估计算法,即无迹粒子滤波(unscented particle filter,UPF),以实现SOC的精确估计.然而,UPF对硬件设备的计算能力要求较高. ...
State estimation of vehicle lithium ion battery based on traceless particle filter
1
2018
... PF的思想基于蒙特卡洛方法,利用粒子集来表示概率,可以用在任何形式的状态空间模型上.相比于KF,PF不对系统做线性假设和后验概率的高斯假设,是一种非线性、非高斯的滤波方法.文献[29]使用PF进行磷酸铁锂离子电池SOC估算,结果显示,其能较好地描述非线性系统的外部特性,显著提升SOC的预测精度,然而容易出现粒子退化问题.文献[30]为解决粒子匮乏、噪声扰动等问题,提出一种改进的估计算法,即无迹粒子滤波(unscented particle filter,UPF),以实现SOC的精确估计.然而,UPF对硬件设备的计算能力要求较高. ...
锂离子电池建模及其荷电状态鲁棒估计
1
2015
... HIF法是以EKF为基础进行改进的一种算法,在HIF中, Q 与 R 是根据wk 与vk 的先验知识来设计的参数,相比于EKF与PF,能够更好地容忍模型不精确性和噪声不确定性[31-32].文献[33]采用HIF算法获得了较高精度和鲁棒性的SOC估计结果.文献[34]采用双HIF算法来进行SOC估计,可以将估计误差稳定在2%以内.大部分HIF算法都能达到较高的精度,但是由于其本身的鲁棒性特点,仍然存在对系统状态和模型不确定性突变的不敏感问题.文献[35]提出基于HIF的非线性观测器估计锂离子电池SOC,实验结果表明,针对不同的工况,该算法可以抑制模型误差,但该算法对模型参数变化的响应较慢. ...
锂离子电池建模及其荷电状态鲁棒估计
1
2015
... HIF法是以EKF为基础进行改进的一种算法,在HIF中, Q 与 R 是根据wk 与vk 的先验知识来设计的参数,相比于EKF与PF,能够更好地容忍模型不精确性和噪声不确定性[31-32].文献[33]采用HIF算法获得了较高精度和鲁棒性的SOC估计结果.文献[34]采用双HIF算法来进行SOC估计,可以将估计误差稳定在2%以内.大部分HIF算法都能达到较高的精度,但是由于其本身的鲁棒性特点,仍然存在对系统状态和模型不确定性突变的不敏感问题.文献[35]提出基于HIF的非线性观测器估计锂离子电池SOC,实验结果表明,针对不同的工况,该算法可以抑制模型误差,但该算法对模型参数变化的响应较慢. ...
A state of charge estimation method based on H-infinity observer for switched systems of lithium-ion nickel-manganese-cobalt batteries
1
2017
... HIF法是以EKF为基础进行改进的一种算法,在HIF中, Q 与 R 是根据wk 与vk 的先验知识来设计的参数,相比于EKF与PF,能够更好地容忍模型不精确性和噪声不确定性[31-32].文献[33]采用HIF算法获得了较高精度和鲁棒性的SOC估计结果.文献[34]采用双HIF算法来进行SOC估计,可以将估计误差稳定在2%以内.大部分HIF算法都能达到较高的精度,但是由于其本身的鲁棒性特点,仍然存在对系统状态和模型不确定性突变的不敏感问题.文献[35]提出基于HIF的非线性观测器估计锂离子电池SOC,实验结果表明,针对不同的工况,该算法可以抑制模型误差,但该算法对模型参数变化的响应较慢. ...
A lithium-ion battery-in-the-loop approach to test and validate multiscale dual H infinity filters for state-of-charge and capacity estimation
1
2018
... HIF法是以EKF为基础进行改进的一种算法,在HIF中, Q 与 R 是根据wk 与vk 的先验知识来设计的参数,相比于EKF与PF,能够更好地容忍模型不精确性和噪声不确定性[31-32].文献[33]采用HIF算法获得了较高精度和鲁棒性的SOC估计结果.文献[34]采用双HIF算法来进行SOC估计,可以将估计误差稳定在2%以内.大部分HIF算法都能达到较高的精度,但是由于其本身的鲁棒性特点,仍然存在对系统状态和模型不确定性突变的不敏感问题.文献[35]提出基于HIF的非线性观测器估计锂离子电池SOC,实验结果表明,针对不同的工况,该算法可以抑制模型误差,但该算法对模型参数变化的响应较慢. ...
A new method for state of charge and capacity estimation of lithium-ion battery based on dual strong tracking adaptive H infinity filter
1
2018
... HIF法是以EKF为基础进行改进的一种算法,在HIF中, Q 与 R 是根据wk 与vk 的先验知识来设计的参数,相比于EKF与PF,能够更好地容忍模型不精确性和噪声不确定性[31-32].文献[33]采用HIF算法获得了较高精度和鲁棒性的SOC估计结果.文献[34]采用双HIF算法来进行SOC估计,可以将估计误差稳定在2%以内.大部分HIF算法都能达到较高的精度,但是由于其本身的鲁棒性特点,仍然存在对系统状态和模型不确定性突变的不敏感问题.文献[35]提出基于HIF的非线性观测器估计锂离子电池SOC,实验结果表明,针对不同的工况,该算法可以抑制模型误差,但该算法对模型参数变化的响应较慢. ...
H-infinity-based nonlinear observer design for state of charge estimation of lithium-ion battery with polynomial parameters
1
2017
... HIF法是以EKF为基础进行改进的一种算法,在HIF中, Q 与 R 是根据wk 与vk 的先验知识来设计的参数,相比于EKF与PF,能够更好地容忍模型不精确性和噪声不确定性[31-32].文献[33]采用HIF算法获得了较高精度和鲁棒性的SOC估计结果.文献[34]采用双HIF算法来进行SOC估计,可以将估计误差稳定在2%以内.大部分HIF算法都能达到较高的精度,但是由于其本身的鲁棒性特点,仍然存在对系统状态和模型不确定性突变的不敏感问题.文献[35]提出基于HIF的非线性观测器估计锂离子电池SOC,实验结果表明,针对不同的工况,该算法可以抑制模型误差,但该算法对模型参数变化的响应较慢. ...
Investigating the error sources of the online state of charge estimation methods for lithium-ion batteries in electric vehicles
1
2018
... 与滤波器类似,基于观测器方法也可通过计算系统误差来实时观测模型状态[36].其中,滑模观测器是一种闭环的状态观测器,输出变量y提供对观测器系统的校正作用.滑膜观测器由于其闭环特点,鲁棒性较强,对电池模型结构和参数扰动的敏感性不高[37],不需要预知噪声的先验信息[38],且其估计精度与PF相近.文献[39]提出了一种基于改进滑模观测器的锂离子电池SOC估算方法,该方法继承了滑模观测器良好的鲁棒性.1.3.2 基于电化学模型的SOC估算方法 ...
一种基于改进离散滑模观测器的锂电池SOC估计方法
1
2018
... 与滤波器类似,基于观测器方法也可通过计算系统误差来实时观测模型状态[36].其中,滑模观测器是一种闭环的状态观测器,输出变量y提供对观测器系统的校正作用.滑膜观测器由于其闭环特点,鲁棒性较强,对电池模型结构和参数扰动的敏感性不高[37],不需要预知噪声的先验信息[38],且其估计精度与PF相近.文献[39]提出了一种基于改进滑模观测器的锂离子电池SOC估算方法,该方法继承了滑模观测器良好的鲁棒性.1.3.2 基于电化学模型的SOC估算方法 ...
一种基于改进离散滑模观测器的锂电池SOC估计方法
1
2018
... 与滤波器类似,基于观测器方法也可通过计算系统误差来实时观测模型状态[36].其中,滑模观测器是一种闭环的状态观测器,输出变量y提供对观测器系统的校正作用.滑膜观测器由于其闭环特点,鲁棒性较强,对电池模型结构和参数扰动的敏感性不高[37],不需要预知噪声的先验信息[38],且其估计精度与PF相近.文献[39]提出了一种基于改进滑模观测器的锂离子电池SOC估算方法,该方法继承了滑模观测器良好的鲁棒性.1.3.2 基于电化学模型的SOC估算方法 ...
基于滑模观测器的锂离子动力电池荷电状态估计
1
2011
... 与滤波器类似,基于观测器方法也可通过计算系统误差来实时观测模型状态[36].其中,滑模观测器是一种闭环的状态观测器,输出变量y提供对观测器系统的校正作用.滑膜观测器由于其闭环特点,鲁棒性较强,对电池模型结构和参数扰动的敏感性不高[37],不需要预知噪声的先验信息[38],且其估计精度与PF相近.文献[39]提出了一种基于改进滑模观测器的锂离子电池SOC估算方法,该方法继承了滑模观测器良好的鲁棒性.1.3.2 基于电化学模型的SOC估算方法 ...
基于滑模观测器的锂离子动力电池荷电状态估计
1
2011
... 与滤波器类似,基于观测器方法也可通过计算系统误差来实时观测模型状态[36].其中,滑模观测器是一种闭环的状态观测器,输出变量y提供对观测器系统的校正作用.滑膜观测器由于其闭环特点,鲁棒性较强,对电池模型结构和参数扰动的敏感性不高[37],不需要预知噪声的先验信息[38],且其估计精度与PF相近.文献[39]提出了一种基于改进滑模观测器的锂离子电池SOC估算方法,该方法继承了滑模观测器良好的鲁棒性.1.3.2 基于电化学模型的SOC估算方法 ...
基于滑模观测器的锂离子电池荷电状态与健康状态估计算法研究
1
2018
... 与滤波器类似,基于观测器方法也可通过计算系统误差来实时观测模型状态[36].其中,滑模观测器是一种闭环的状态观测器,输出变量y提供对观测器系统的校正作用.滑膜观测器由于其闭环特点,鲁棒性较强,对电池模型结构和参数扰动的敏感性不高[37],不需要预知噪声的先验信息[38],且其估计精度与PF相近.文献[39]提出了一种基于改进滑模观测器的锂离子电池SOC估算方法,该方法继承了滑模观测器良好的鲁棒性.1.3.2 基于电化学模型的SOC估算方法 ...
基于滑模观测器的锂离子电池荷电状态与健康状态估计算法研究
1
2018
... 与滤波器类似,基于观测器方法也可通过计算系统误差来实时观测模型状态[36].其中,滑模观测器是一种闭环的状态观测器,输出变量y提供对观测器系统的校正作用.滑膜观测器由于其闭环特点,鲁棒性较强,对电池模型结构和参数扰动的敏感性不高[37],不需要预知噪声的先验信息[38],且其估计精度与PF相近.文献[39]提出了一种基于改进滑模观测器的锂离子电池SOC估算方法,该方法继承了滑模观测器良好的鲁棒性.1.3.2 基于电化学模型的SOC估算方法 ...
Modeling of galvanostatic charge and discharge of the lithium/polymer/insertion cell
1
1993
... 虽然外特性模型计算简单,然而由于无法反映电池内部机理,所以无法完全映射电池内部机理变化造成的状态变化.锂离子电池电化学模型能深入描述电池内部的微观反应,具有更明确的物理含义.电池电化学模型主要分为3类:准二维(pseudo two-dimensional,P2D)模型[40] 、单粒子(single particle,SP)模型、简化P2D模型.3种模型对比如表1所示. ...
锂离子动力电池电化学模型建模与老化状态识别研究
1
2018
... 由于P2D模型控制方程过于复杂,而单粒子模型的精度较差,许多学者针对不同的应用场景,对P2D模型采用不同的简化方式来保证对应场景的计算精度并降低计算量.现有的简化方式主要包括几何结构简化、固液相扩散过程简化以及通过数学算法进行变换的简化.例如,文献[41]基于多孔电极理论和浓溶液理论建立了数学方程,描述动力电池在充放电过程中其内部的物理、化学行为,并使用有限分析方法对PDE进行了网格化和离散化,使其降阶为常微分方程.但简化模型无法解决P2D参数过多的固有问题,且会在不同程度上降低模型精度,如何平衡计算量与模型精度仍然值得思考[42-45]. ...
锂离子动力电池电化学模型建模与老化状态识别研究
1
2018
... 由于P2D模型控制方程过于复杂,而单粒子模型的精度较差,许多学者针对不同的应用场景,对P2D模型采用不同的简化方式来保证对应场景的计算精度并降低计算量.现有的简化方式主要包括几何结构简化、固液相扩散过程简化以及通过数学算法进行变换的简化.例如,文献[41]基于多孔电极理论和浓溶液理论建立了数学方程,描述动力电池在充放电过程中其内部的物理、化学行为,并使用有限分析方法对PDE进行了网格化和离散化,使其降阶为常微分方程.但简化模型无法解决P2D参数过多的固有问题,且会在不同程度上降低模型精度,如何平衡计算量与模型精度仍然值得思考[42-45]. ...
Reduced-order electrochemical model parameters identification and state of charge estimation for healthy and aged Li-Ion batteries:part Ⅱ:aged battery model and state of charge estimation
1
2014
... 由于P2D模型控制方程过于复杂,而单粒子模型的精度较差,许多学者针对不同的应用场景,对P2D模型采用不同的简化方式来保证对应场景的计算精度并降低计算量.现有的简化方式主要包括几何结构简化、固液相扩散过程简化以及通过数学算法进行变换的简化.例如,文献[41]基于多孔电极理论和浓溶液理论建立了数学方程,描述动力电池在充放电过程中其内部的物理、化学行为,并使用有限分析方法对PDE进行了网格化和离散化,使其降阶为常微分方程.但简化模型无法解决P2D参数过多的固有问题,且会在不同程度上降低模型精度,如何平衡计算量与模型精度仍然值得思考[42-45]. ...
A review of fractional-order techniques applied to lithium-ion batteries,lead-acid batteries,and supercapacitors
0
2018
Capacity fade estimation in electric vehicles Li-ion batteries using artificial neural networks
0
2013
Battery state estimation for a single particle model with electrolyte dynamics
1
2017
... 由于P2D模型控制方程过于复杂,而单粒子模型的精度较差,许多学者针对不同的应用场景,对P2D模型采用不同的简化方式来保证对应场景的计算精度并降低计算量.现有的简化方式主要包括几何结构简化、固液相扩散过程简化以及通过数学算法进行变换的简化.例如,文献[41]基于多孔电极理论和浓溶液理论建立了数学方程,描述动力电池在充放电过程中其内部的物理、化学行为,并使用有限分析方法对PDE进行了网格化和离散化,使其降阶为常微分方程.但简化模型无法解决P2D参数过多的固有问题,且会在不同程度上降低模型精度,如何平衡计算量与模型精度仍然值得思考[42-45]. ...
Experiment-driven electrochemical modeling and systematic parameterization for a lithium-ion battery cell
1
2010
... 在基于电化学模型计算SOC时,不同于式(1),电化学机理模型(如P2D模型和SP模型)的SOC分为表面SOC和平均SOC[46],根据电化学理论可分别表示为: ...
基于神经网络的磷酸铁锂电池SOC预测研究
1
2011
... 电池参数与SOC之间的关系复杂且非线性,用传统数学方法建立模型很困难,且可靠性低[47].基于数据驱动的方法不依赖电池的数学模型,可直接依靠系统输入与输出间的映射关系估算电池SOC.目前,使用较为广泛的数据驱动法包括神经网络及其改进算法、回归分析法及其改进算法等. ...
基于神经网络的磷酸铁锂电池SOC预测研究
1
2011
... 电池参数与SOC之间的关系复杂且非线性,用传统数学方法建立模型很困难,且可靠性低[47].基于数据驱动的方法不依赖电池的数学模型,可直接依靠系统输入与输出间的映射关系估算电池SOC.目前,使用较为广泛的数据驱动法包括神经网络及其改进算法、回归分析法及其改进算法等. ...
State of charge estimation for electric vehicle power battery using advanced machine learning algorithm under diversified drive cycles
1
2018
... 基于神经网络的SOC估算方法是以电池运行数据(如电压、电流等参数)作为输入,以SOC作为输出结果,通过样本数据对系统进行训练,以此来寻找各参数之间的映射关系[48]. ...
基于神经网络模型的动力电池SOC估计研究
1
2015
... 反向传播(back propagation,BP)神经网络是典型的神经网络算法,其网络结构简单,具有较强的非线性映射能力.文献[49]对电池荷电状态的影响因素进行了归纳,提出了基于BP神经网络的动力电池荷电状态估计方法.然而BP神经网络容易陷入局部最优;另外,网络结构选择不一,容易出现不收敛情况. ...
基于神经网络模型的动力电池SOC估计研究
1
2015
... 反向传播(back propagation,BP)神经网络是典型的神经网络算法,其网络结构简单,具有较强的非线性映射能力.文献[49]对电池荷电状态的影响因素进行了归纳,提出了基于BP神经网络的动力电池荷电状态估计方法.然而BP神经网络容易陷入局部最优;另外,网络结构选择不一,容易出现不收敛情况. ...
基于RNN的锂离子电池SOC估算研究进展
1
2021
... 循环神经网络(recurrent neural network,RNN)是一种用于处理序列数据的神经网络,对于SOC等时序数据具有较好的估算效果[50].RNN以序列数据为输入,在序列的演进方向进行递归且所有循环节点按链式连接的递归神经网络,但其在训练时,会出现“梯度消失”和“梯度爆炸”的现象.为了解决这2个问题,一些学者提出了长短期记忆(long short-term memory,LSTM)神经网络[51-53]、门控循环单元(gated recurrent unit,GRU)神经网络[54-55]以及双向长短期记忆神经网络(Bi-LSTM)[56]等.LSTM解决长序列训练过程中的梯度消失和梯度爆炸问题,相比于普通的RNN,LSTM能够在更长的序列中有更好的表现.GRU是LSTM的改进,其精度与LSTM相当,但参数更少,计算速度更快. ...
基于RNN的锂离子电池SOC估算研究进展
1
2021
... 循环神经网络(recurrent neural network,RNN)是一种用于处理序列数据的神经网络,对于SOC等时序数据具有较好的估算效果[50].RNN以序列数据为输入,在序列的演进方向进行递归且所有循环节点按链式连接的递归神经网络,但其在训练时,会出现“梯度消失”和“梯度爆炸”的现象.为了解决这2个问题,一些学者提出了长短期记忆(long short-term memory,LSTM)神经网络[51-53]、门控循环单元(gated recurrent unit,GRU)神经网络[54-55]以及双向长短期记忆神经网络(Bi-LSTM)[56]等.LSTM解决长序列训练过程中的梯度消失和梯度爆炸问题,相比于普通的RNN,LSTM能够在更长的序列中有更好的表现.GRU是LSTM的改进,其精度与LSTM相当,但参数更少,计算速度更快. ...
基于改进LSTM的脉冲大倍率工况下锂电池SOC估计
1
2021
... 循环神经网络(recurrent neural network,RNN)是一种用于处理序列数据的神经网络,对于SOC等时序数据具有较好的估算效果[50].RNN以序列数据为输入,在序列的演进方向进行递归且所有循环节点按链式连接的递归神经网络,但其在训练时,会出现“梯度消失”和“梯度爆炸”的现象.为了解决这2个问题,一些学者提出了长短期记忆(long short-term memory,LSTM)神经网络[51-53]、门控循环单元(gated recurrent unit,GRU)神经网络[54-55]以及双向长短期记忆神经网络(Bi-LSTM)[56]等.LSTM解决长序列训练过程中的梯度消失和梯度爆炸问题,相比于普通的RNN,LSTM能够在更长的序列中有更好的表现.GRU是LSTM的改进,其精度与LSTM相当,但参数更少,计算速度更快. ...
基于改进LSTM的脉冲大倍率工况下锂电池SOC估计
1
2021
... 循环神经网络(recurrent neural network,RNN)是一种用于处理序列数据的神经网络,对于SOC等时序数据具有较好的估算效果[50].RNN以序列数据为输入,在序列的演进方向进行递归且所有循环节点按链式连接的递归神经网络,但其在训练时,会出现“梯度消失”和“梯度爆炸”的现象.为了解决这2个问题,一些学者提出了长短期记忆(long short-term memory,LSTM)神经网络[51-53]、门控循环单元(gated recurrent unit,GRU)神经网络[54-55]以及双向长短期记忆神经网络(Bi-LSTM)[56]等.LSTM解决长序列训练过程中的梯度消失和梯度爆炸问题,相比于普通的RNN,LSTM能够在更长的序列中有更好的表现.GRU是LSTM的改进,其精度与LSTM相当,但参数更少,计算速度更快. ...
An intrusion detection system using a deep neural network with gated recurrent units
0
2018
基于LSTM神经网络的动力电池SOC估算研究
1
2020
... 循环神经网络(recurrent neural network,RNN)是一种用于处理序列数据的神经网络,对于SOC等时序数据具有较好的估算效果[50].RNN以序列数据为输入,在序列的演进方向进行递归且所有循环节点按链式连接的递归神经网络,但其在训练时,会出现“梯度消失”和“梯度爆炸”的现象.为了解决这2个问题,一些学者提出了长短期记忆(long short-term memory,LSTM)神经网络[51-53]、门控循环单元(gated recurrent unit,GRU)神经网络[54-55]以及双向长短期记忆神经网络(Bi-LSTM)[56]等.LSTM解决长序列训练过程中的梯度消失和梯度爆炸问题,相比于普通的RNN,LSTM能够在更长的序列中有更好的表现.GRU是LSTM的改进,其精度与LSTM相当,但参数更少,计算速度更快. ...
基于LSTM神经网络的动力电池SOC估算研究
1
2020
... 循环神经网络(recurrent neural network,RNN)是一种用于处理序列数据的神经网络,对于SOC等时序数据具有较好的估算效果[50].RNN以序列数据为输入,在序列的演进方向进行递归且所有循环节点按链式连接的递归神经网络,但其在训练时,会出现“梯度消失”和“梯度爆炸”的现象.为了解决这2个问题,一些学者提出了长短期记忆(long short-term memory,LSTM)神经网络[51-53]、门控循环单元(gated recurrent unit,GRU)神经网络[54-55]以及双向长短期记忆神经网络(Bi-LSTM)[56]等.LSTM解决长序列训练过程中的梯度消失和梯度爆炸问题,相比于普通的RNN,LSTM能够在更长的序列中有更好的表现.GRU是LSTM的改进,其精度与LSTM相当,但参数更少,计算速度更快. ...
基于门控循环单元神经网络和Huber-M估计鲁棒卡尔曼滤波融合方法的锂离子电池荷电状态估算方法
1
2020
... 循环神经网络(recurrent neural network,RNN)是一种用于处理序列数据的神经网络,对于SOC等时序数据具有较好的估算效果[50].RNN以序列数据为输入,在序列的演进方向进行递归且所有循环节点按链式连接的递归神经网络,但其在训练时,会出现“梯度消失”和“梯度爆炸”的现象.为了解决这2个问题,一些学者提出了长短期记忆(long short-term memory,LSTM)神经网络[51-53]、门控循环单元(gated recurrent unit,GRU)神经网络[54-55]以及双向长短期记忆神经网络(Bi-LSTM)[56]等.LSTM解决长序列训练过程中的梯度消失和梯度爆炸问题,相比于普通的RNN,LSTM能够在更长的序列中有更好的表现.GRU是LSTM的改进,其精度与LSTM相当,但参数更少,计算速度更快. ...
基于门控循环单元神经网络和Huber-M估计鲁棒卡尔曼滤波融合方法的锂离子电池荷电状态估算方法
1
2020
... 循环神经网络(recurrent neural network,RNN)是一种用于处理序列数据的神经网络,对于SOC等时序数据具有较好的估算效果[50].RNN以序列数据为输入,在序列的演进方向进行递归且所有循环节点按链式连接的递归神经网络,但其在训练时,会出现“梯度消失”和“梯度爆炸”的现象.为了解决这2个问题,一些学者提出了长短期记忆(long short-term memory,LSTM)神经网络[51-53]、门控循环单元(gated recurrent unit,GRU)神经网络[54-55]以及双向长短期记忆神经网络(Bi-LSTM)[56]等.LSTM解决长序列训练过程中的梯度消失和梯度爆炸问题,相比于普通的RNN,LSTM能够在更长的序列中有更好的表现.GRU是LSTM的改进,其精度与LSTM相当,但参数更少,计算速度更快. ...
基于门控循环单元神经网络的锂离子电池宽温度SOC估计
1
2021
... 循环神经网络(recurrent neural network,RNN)是一种用于处理序列数据的神经网络,对于SOC等时序数据具有较好的估算效果[50].RNN以序列数据为输入,在序列的演进方向进行递归且所有循环节点按链式连接的递归神经网络,但其在训练时,会出现“梯度消失”和“梯度爆炸”的现象.为了解决这2个问题,一些学者提出了长短期记忆(long short-term memory,LSTM)神经网络[51-53]、门控循环单元(gated recurrent unit,GRU)神经网络[54-55]以及双向长短期记忆神经网络(Bi-LSTM)[56]等.LSTM解决长序列训练过程中的梯度消失和梯度爆炸问题,相比于普通的RNN,LSTM能够在更长的序列中有更好的表现.GRU是LSTM的改进,其精度与LSTM相当,但参数更少,计算速度更快. ...
基于门控循环单元神经网络的锂离子电池宽温度SOC估计
1
2021
... 循环神经网络(recurrent neural network,RNN)是一种用于处理序列数据的神经网络,对于SOC等时序数据具有较好的估算效果[50].RNN以序列数据为输入,在序列的演进方向进行递归且所有循环节点按链式连接的递归神经网络,但其在训练时,会出现“梯度消失”和“梯度爆炸”的现象.为了解决这2个问题,一些学者提出了长短期记忆(long short-term memory,LSTM)神经网络[51-53]、门控循环单元(gated recurrent unit,GRU)神经网络[54-55]以及双向长短期记忆神经网络(Bi-LSTM)[56]等.LSTM解决长序列训练过程中的梯度消失和梯度爆炸问题,相比于普通的RNN,LSTM能够在更长的序列中有更好的表现.GRU是LSTM的改进,其精度与LSTM相当,但参数更少,计算速度更快. ...
基于Bi-LSTM/Bi-GRU循环神经网络的锂电池SOC估计
1
2021
... 循环神经网络(recurrent neural network,RNN)是一种用于处理序列数据的神经网络,对于SOC等时序数据具有较好的估算效果[50].RNN以序列数据为输入,在序列的演进方向进行递归且所有循环节点按链式连接的递归神经网络,但其在训练时,会出现“梯度消失”和“梯度爆炸”的现象.为了解决这2个问题,一些学者提出了长短期记忆(long short-term memory,LSTM)神经网络[51-53]、门控循环单元(gated recurrent unit,GRU)神经网络[54-55]以及双向长短期记忆神经网络(Bi-LSTM)[56]等.LSTM解决长序列训练过程中的梯度消失和梯度爆炸问题,相比于普通的RNN,LSTM能够在更长的序列中有更好的表现.GRU是LSTM的改进,其精度与LSTM相当,但参数更少,计算速度更快. ...
基于Bi-LSTM/Bi-GRU循环神经网络的锂电池SOC估计
1
2021
... 循环神经网络(recurrent neural network,RNN)是一种用于处理序列数据的神经网络,对于SOC等时序数据具有较好的估算效果[50].RNN以序列数据为输入,在序列的演进方向进行递归且所有循环节点按链式连接的递归神经网络,但其在训练时,会出现“梯度消失”和“梯度爆炸”的现象.为了解决这2个问题,一些学者提出了长短期记忆(long short-term memory,LSTM)神经网络[51-53]、门控循环单元(gated recurrent unit,GRU)神经网络[54-55]以及双向长短期记忆神经网络(Bi-LSTM)[56]等.LSTM解决长序列训练过程中的梯度消失和梯度爆炸问题,相比于普通的RNN,LSTM能够在更长的序列中有更好的表现.GRU是LSTM的改进,其精度与LSTM相当,但参数更少,计算速度更快. ...
基于SVM的锂电池SOC估算
1
2016
... 支持向量机(support vector machine,SVM)是一种使用分类与回归分析技术来处理数据的算法[57].该方法在高维模式识别、非线性回归等问题中取得了较好效果.但当样本规模扩增到一定程度时,SVM优化所带来的复杂度会显著提升,同时模型精度也会有所下降[58-59].针对上述问题,文献[58]提出了一种最小二乘SVM,将标准SVM的学习问题转化为解线性方程组问题,变量更少、运算量更小,具有更快的求解速度和更好的鲁棒性. ...
基于SVM的锂电池SOC估算
1
2016
... 支持向量机(support vector machine,SVM)是一种使用分类与回归分析技术来处理数据的算法[57].该方法在高维模式识别、非线性回归等问题中取得了较好效果.但当样本规模扩增到一定程度时,SVM优化所带来的复杂度会显著提升,同时模型精度也会有所下降[58-59].针对上述问题,文献[58]提出了一种最小二乘SVM,将标准SVM的学习问题转化为解线性方程组问题,变量更少、运算量更小,具有更快的求解速度和更好的鲁棒性. ...
基于在线LS-SVM的动力电池SOC估算方法研究
2
2017
... 支持向量机(support vector machine,SVM)是一种使用分类与回归分析技术来处理数据的算法[57].该方法在高维模式识别、非线性回归等问题中取得了较好效果.但当样本规模扩增到一定程度时,SVM优化所带来的复杂度会显著提升,同时模型精度也会有所下降[58-59].针对上述问题,文献[58]提出了一种最小二乘SVM,将标准SVM的学习问题转化为解线性方程组问题,变量更少、运算量更小,具有更快的求解速度和更好的鲁棒性. ...
... .针对上述问题,文献[58]提出了一种最小二乘SVM,将标准SVM的学习问题转化为解线性方程组问题,变量更少、运算量更小,具有更快的求解速度和更好的鲁棒性. ...
基于在线LS-SVM的动力电池SOC估算方法研究
2
2017
... 支持向量机(support vector machine,SVM)是一种使用分类与回归分析技术来处理数据的算法[57].该方法在高维模式识别、非线性回归等问题中取得了较好效果.但当样本规模扩增到一定程度时,SVM优化所带来的复杂度会显著提升,同时模型精度也会有所下降[58-59].针对上述问题,文献[58]提出了一种最小二乘SVM,将标准SVM的学习问题转化为解线性方程组问题,变量更少、运算量更小,具有更快的求解速度和更好的鲁棒性. ...
... .针对上述问题,文献[58]提出了一种最小二乘SVM,将标准SVM的学习问题转化为解线性方程组问题,变量更少、运算量更小,具有更快的求解速度和更好的鲁棒性. ...
基于支持向量机的在线暂态稳定故障筛选
1
2019
... 支持向量机(support vector machine,SVM)是一种使用分类与回归分析技术来处理数据的算法[57].该方法在高维模式识别、非线性回归等问题中取得了较好效果.但当样本规模扩增到一定程度时,SVM优化所带来的复杂度会显著提升,同时模型精度也会有所下降[58-59].针对上述问题,文献[58]提出了一种最小二乘SVM,将标准SVM的学习问题转化为解线性方程组问题,变量更少、运算量更小,具有更快的求解速度和更好的鲁棒性. ...
基于支持向量机的在线暂态稳定故障筛选
1
2019
... 支持向量机(support vector machine,SVM)是一种使用分类与回归分析技术来处理数据的算法[57].该方法在高维模式识别、非线性回归等问题中取得了较好效果.但当样本规模扩增到一定程度时,SVM优化所带来的复杂度会显著提升,同时模型精度也会有所下降[58-59].针对上述问题,文献[58]提出了一种最小二乘SVM,将标准SVM的学习问题转化为解线性方程组问题,变量更少、运算量更小,具有更快的求解速度和更好的鲁棒性. ...
基于注意力机制和CNN-LSTM融合模型的锂电池SOC预测
1
... 由于各模型法与各数据驱动法均有其优缺点,因此,部分学者采用多类方法融合估算锂离子电池SOC,优势互补.融合类型包括模型法与数据驱动法融合、不同数据驱动法融合等.文献[60]提出了注意力机制、卷积神经网络(convolutional neural networks,CNN)和LSTM的融合模型,将当前时刻的SOC与多个历史时刻的锂电池放电数据建立映射关系,提升了SOC的估算精度.文献[61]基于Thevenin等效电路模型,同时结合神经网络来分析开路电压和SOC之间的非线性关系,并使用改进的UKF来估算锂离子电池SOC,相比于普通UKF精度更高. ...
基于注意力机制和CNN-LSTM融合模型的锂电池SOC预测
1
... 由于各模型法与各数据驱动法均有其优缺点,因此,部分学者采用多类方法融合估算锂离子电池SOC,优势互补.融合类型包括模型法与数据驱动法融合、不同数据驱动法融合等.文献[60]提出了注意力机制、卷积神经网络(convolutional neural networks,CNN)和LSTM的融合模型,将当前时刻的SOC与多个历史时刻的锂电池放电数据建立映射关系,提升了SOC的估算精度.文献[61]基于Thevenin等效电路模型,同时结合神经网络来分析开路电压和SOC之间的非线性关系,并使用改进的UKF来估算锂离子电池SOC,相比于普通UKF精度更高. ...
基于AFFDRLS-AHIF 对动力锂离子电池单体SOC估计
1
2020
... 由于各模型法与各数据驱动法均有其优缺点,因此,部分学者采用多类方法融合估算锂离子电池SOC,优势互补.融合类型包括模型法与数据驱动法融合、不同数据驱动法融合等.文献[60]提出了注意力机制、卷积神经网络(convolutional neural networks,CNN)和LSTM的融合模型,将当前时刻的SOC与多个历史时刻的锂电池放电数据建立映射关系,提升了SOC的估算精度.文献[61]基于Thevenin等效电路模型,同时结合神经网络来分析开路电压和SOC之间的非线性关系,并使用改进的UKF来估算锂离子电池SOC,相比于普通UKF精度更高. ...
基于AFFDRLS-AHIF 对动力锂离子电池单体SOC估计
1
2020
... 由于各模型法与各数据驱动法均有其优缺点,因此,部分学者采用多类方法融合估算锂离子电池SOC,优势互补.融合类型包括模型法与数据驱动法融合、不同数据驱动法融合等.文献[60]提出了注意力机制、卷积神经网络(convolutional neural networks,CNN)和LSTM的融合模型,将当前时刻的SOC与多个历史时刻的锂电池放电数据建立映射关系,提升了SOC的估算精度.文献[61]基于Thevenin等效电路模型,同时结合神经网络来分析开路电压和SOC之间的非线性关系,并使用改进的UKF来估算锂离子电池SOC,相比于普通UKF精度更高. ...
State-of-health monitoring of lithiumion batteries in electric vehicles by on-board internal resistance estimation
1
2011
... SOH由随电池老化而改变的电池参数表征.其中可用容量定义的SOH应用最为广泛[62],如式(11)所示,容量随电池老化呈下降趋势. ...
考虑储能动态运行特性的充电站光储容量优化配置模型
1
2021
... 式中:为用容量表征的SOH;Cact为当前实际可用容量;Cini为电池初始容量.一般电池容量衰退至初始容量的80%时寿命终止[63]. ...
考虑储能动态运行特性的充电站光储容量优化配置模型
1
2021
... 式中:为用容量表征的SOH;Cact为当前实际可用容量;Cini为电池初始容量.一般电池容量衰退至初始容量的80%时寿命终止[63]. ...
基于特征频率阻抗的锂离子电池健康状态评估
1
... SOH计算方法分为基于实验的估计方法[64]、基于模型的估计方法与基于数据驱动的估计方法3类.由于SOH一般通过容量或内阻定义,因此通过实验测量电池剩余最大可用容量与内阻即可计算电池SOH.对于模型法,由于SOH也为一种电池状态,因此可用与SOC估计类似的方法来估计电池SOH[65-68].数据驱动法也基本一致[69-70],此处不再赘述. ...
基于特征频率阻抗的锂离子电池健康状态评估
1
... SOH计算方法分为基于实验的估计方法[64]、基于模型的估计方法与基于数据驱动的估计方法3类.由于SOH一般通过容量或内阻定义,因此通过实验测量电池剩余最大可用容量与内阻即可计算电池SOH.对于模型法,由于SOH也为一种电池状态,因此可用与SOC估计类似的方法来估计电池SOH[65-68].数据驱动法也基本一致[69-70],此处不再赘述. ...
State of charge (SOC) and state of health (SOH) estimation on lithium polymer battery via Kalman filter
1
2016
... SOH计算方法分为基于实验的估计方法[64]、基于模型的估计方法与基于数据驱动的估计方法3类.由于SOH一般通过容量或内阻定义,因此通过实验测量电池剩余最大可用容量与内阻即可计算电池SOH.对于模型法,由于SOH也为一种电池状态,因此可用与SOC估计类似的方法来估计电池SOH[65-68].数据驱动法也基本一致[69-70],此处不再赘述. ...
锂离子电池荷电状态与健康状态估计方法
0
2021
锂离子电池荷电状态与健康状态估计方法
0
2021
基于电化学模型的锂离子电池健康状态估算
0
2022
基于电化学模型的锂离子电池健康状态估算
0
2022
基于电化学热耦合模型的锂离子电池老化状态估计
2
2021
... SOH计算方法分为基于实验的估计方法[64]、基于模型的估计方法与基于数据驱动的估计方法3类.由于SOH一般通过容量或内阻定义,因此通过实验测量电池剩余最大可用容量与内阻即可计算电池SOH.对于模型法,由于SOH也为一种电池状态,因此可用与SOC估计类似的方法来估计电池SOH[65-68].数据驱动法也基本一致[69-70],此处不再赘述. ...
... 电化学模型根据电池内部的物理和化学反应,推导出与机理相关的电池性能衰退机制,如锂离子损失、活性物质损失和电导率损失等.然而,模型参数一般难以测量,动态准确度较差.同时,电池退化特征及参数多[84].文献[68]提出的与电池老化相关的电化学模型参数超过15个.因此,基于电化学模型的RUL预测方法难以实际应用. ...
基于电化学热耦合模型的锂离子电池老化状态估计
2
2021
... SOH计算方法分为基于实验的估计方法[64]、基于模型的估计方法与基于数据驱动的估计方法3类.由于SOH一般通过容量或内阻定义,因此通过实验测量电池剩余最大可用容量与内阻即可计算电池SOH.对于模型法,由于SOH也为一种电池状态,因此可用与SOC估计类似的方法来估计电池SOH[65-68].数据驱动法也基本一致[69-70],此处不再赘述. ...
... 电化学模型根据电池内部的物理和化学反应,推导出与机理相关的电池性能衰退机制,如锂离子损失、活性物质损失和电导率损失等.然而,模型参数一般难以测量,动态准确度较差.同时,电池退化特征及参数多[84].文献[68]提出的与电池老化相关的电化学模型参数超过15个.因此,基于电化学模型的RUL预测方法难以实际应用. ...
Online estimation algorithm of SOC and SOH using neural network for lithium battery
1
2021
... SOH计算方法分为基于实验的估计方法[64]、基于模型的估计方法与基于数据驱动的估计方法3类.由于SOH一般通过容量或内阻定义,因此通过实验测量电池剩余最大可用容量与内阻即可计算电池SOH.对于模型法,由于SOH也为一种电池状态,因此可用与SOC估计类似的方法来估计电池SOH[65-68].数据驱动法也基本一致[69-70],此处不再赘述. ...
Deep neural network based SOH monitoring of battery module
1
2019
... SOH计算方法分为基于实验的估计方法[64]、基于模型的估计方法与基于数据驱动的估计方法3类.由于SOH一般通过容量或内阻定义,因此通过实验测量电池剩余最大可用容量与内阻即可计算电池SOH.对于模型法,由于SOH也为一种电池状态,因此可用与SOC估计类似的方法来估计电池SOH[65-68].数据驱动法也基本一致[69-70],此处不再赘述. ...
高能量密度锂离子电池老化半经验模型
1
2022
... 根据老化机制建立的半经验模型可以考虑到不同的使用条件对电池老化性能的影响.针对影响电池老化的应力因子[71],建立基于Arrhenius公式(式(18))、逆幂律公式[72-73](式(19))和双指数公式等的应力模型. ...
高能量密度锂离子电池老化半经验模型
1
2022
... 根据老化机制建立的半经验模型可以考虑到不同的使用条件对电池老化性能的影响.针对影响电池老化的应力因子[71],建立基于Arrhenius公式(式(18))、逆幂律公式[72-73](式(19))和双指数公式等的应力模型. ...
1
2002
... 根据老化机制建立的半经验模型可以考虑到不同的使用条件对电池老化性能的影响.针对影响电池老化的应力因子[71],建立基于Arrhenius公式(式(18))、逆幂律公式[72-73](式(19))和双指数公式等的应力模型. ...
1
2000
... 根据老化机制建立的半经验模型可以考虑到不同的使用条件对电池老化性能的影响.针对影响电池老化的应力因子[71],建立基于Arrhenius公式(式(18))、逆幂律公式[72-73](式(19))和双指数公式等的应力模型. ...
Modeling of lithium-ion battery degradation for cell life assessment
1
2018
... 1)电池参数,如平均SOC[74]等; ...
Modeling the capacity degradation of LiFePO4 graphite batteries based on stress coupling analysis
1
2011
... 2)运行工况,如充放电倍率、充放电截止电压[75]、放电深度(depth of discharge,DOD)[76-77]、安时吞吐量等; ...
Modeling lithium ion battery degradation in electric vehicles
1
2010
... 2)运行工况,如充放电倍率、充放电截止电压[75]、放电深度(depth of discharge,DOD)[76-77]、安时吞吐量等; ...
A battery life prediction method for hybrid power applications
1
1997
... 2)运行工况,如充放电倍率、充放电截止电压[75]、放电深度(depth of discharge,DOD)[76-77]、安时吞吐量等; ...
Development of a lifetime prediction model for lithium-ion batteries based on extended accelerated aging test data
1
2012
Prognostics of lithium-ion batteries based on relevance vectors and a conditional three-parameter capacity degradation model
1
2013
... 通过将不同应力因子的衰退率耦合即可获取综合容量衰退率.将综合衰退率代入电池老化的半经验模型公式中即可计算RUL.文献[79]在双指数公式基础上建立了三参数容量衰退模型,结果表明该模型比双指数公式预测效果更好.文献[80]考虑到LFP电池在不同DOD下循环时放电量的不同,建立了容量关于温度、倍率以及安时吞吐量的半经验模型.除了温度与倍率外,文献[81]还考虑了截止电压对LFP电池容量与内阻的影响,同时探究了双影响因子组合对电池老化的耦合作用.文献[82]基于固体电解质界面膜的形成机理,建立了考虑平均SOC、DOD等应力因子的容量衰退模型. ...
Cycle-life model for graphite-LiFePO4 cells
1
2010
... 通过将不同应力因子的衰退率耦合即可获取综合容量衰退率.将综合衰退率代入电池老化的半经验模型公式中即可计算RUL.文献[79]在双指数公式基础上建立了三参数容量衰退模型,结果表明该模型比双指数公式预测效果更好.文献[80]考虑到LFP电池在不同DOD下循环时放电量的不同,建立了容量关于温度、倍率以及安时吞吐量的半经验模型.除了温度与倍率外,文献[81]还考虑了截止电压对LFP电池容量与内阻的影响,同时探究了双影响因子组合对电池老化的耦合作用.文献[82]基于固体电解质界面膜的形成机理,建立了考虑平均SOC、DOD等应力因子的容量衰退模型. ...
Modeling the capacity degradation of LiFePO4/graphite batteries based on stress coupling analysis
1
2011
... 通过将不同应力因子的衰退率耦合即可获取综合容量衰退率.将综合衰退率代入电池老化的半经验模型公式中即可计算RUL.文献[79]在双指数公式基础上建立了三参数容量衰退模型,结果表明该模型比双指数公式预测效果更好.文献[80]考虑到LFP电池在不同DOD下循环时放电量的不同,建立了容量关于温度、倍率以及安时吞吐量的半经验模型.除了温度与倍率外,文献[81]还考虑了截止电压对LFP电池容量与内阻的影响,同时探究了双影响因子组合对电池老化的耦合作用.文献[82]基于固体电解质界面膜的形成机理,建立了考虑平均SOC、DOD等应力因子的容量衰退模型. ...
Modeling of lithium-ion battery degradation for cell life assessment
1
2018
... 通过将不同应力因子的衰退率耦合即可获取综合容量衰退率.将综合衰退率代入电池老化的半经验模型公式中即可计算RUL.文献[79]在双指数公式基础上建立了三参数容量衰退模型,结果表明该模型比双指数公式预测效果更好.文献[80]考虑到LFP电池在不同DOD下循环时放电量的不同,建立了容量关于温度、倍率以及安时吞吐量的半经验模型.除了温度与倍率外,文献[81]还考虑了截止电压对LFP电池容量与内阻的影响,同时探究了双影响因子组合对电池老化的耦合作用.文献[82]基于固体电解质界面膜的形成机理,建立了考虑平均SOC、DOD等应力因子的容量衰退模型. ...
Operational reliability modeling and assessment of battery energy storage based on lithium-ion battery lifetime degradation
1
2021
... 然而当电池运行工况剧烈变化时,考虑应力因子的半经验模型不再适用,且大部分研究均针对电池容量>80%时的老化特性,对容量<80%的情况罕有研究,而固定的公式难以适应电池全生命周期的RUL预测[83]. ...
1
2002
... 电化学模型根据电池内部的物理和化学反应,推导出与机理相关的电池性能衰退机制,如锂离子损失、活性物质损失和电导率损失等.然而,模型参数一般难以测量,动态准确度较差.同时,电池退化特征及参数多[84].文献[68]提出的与电池老化相关的电化学模型参数超过15个.因此,基于电化学模型的RUL预测方法难以实际应用. ...
Short-term wind speed prediction using empirical wavelet transform and Gaussian process regression
1
2015
... 现有的方法同样包括神经网络、回归算法以及其他方法,比如人工神经网络(artificial neural network,ANN)、自回归(autoregressive,AR)、高斯过程回归(Gaussian process regression) [85-86]等.文献[87]利用粒子群优化算法改进的AR模型进行在线预测.AR模型的计算简单,但预测结果没有不确定性结果表达式.文献[88]提出了基于差分整合移动平均自回归(autoregressive integrated moving average,ARIMA)模型的RUL预测方法,然而ARIMA模型要求时序数据的平稳性,对电池运行工况有较高要求.文献[89]使用动态递归神经网络(dynamically driven recurrent network,DDRN)来降低网络结构的复杂性,提升算法鲁棒性,然而DDRN容易出现梯度消失的问题.除了数据驱动法本身的问题,直接数据驱动法在RUL预测方面还存在以下问题: ...
Battery state-of-charge estimation based on regular/recurrent gaussian process regression
1
2018
... 现有的方法同样包括神经网络、回归算法以及其他方法,比如人工神经网络(artificial neural network,ANN)、自回归(autoregressive,AR)、高斯过程回归(Gaussian process regression) [85-86]等.文献[87]利用粒子群优化算法改进的AR模型进行在线预测.AR模型的计算简单,但预测结果没有不确定性结果表达式.文献[88]提出了基于差分整合移动平均自回归(autoregressive integrated moving average,ARIMA)模型的RUL预测方法,然而ARIMA模型要求时序数据的平稳性,对电池运行工况有较高要求.文献[89]使用动态递归神经网络(dynamically driven recurrent network,DDRN)来降低网络结构的复杂性,提升算法鲁棒性,然而DDRN容易出现梯度消失的问题.除了数据驱动法本身的问题,直接数据驱动法在RUL预测方面还存在以下问题: ...
An improved autoregressive model by particle swarm optimization for prognostics of lithium-ion batteries
1
2013
... 现有的方法同样包括神经网络、回归算法以及其他方法,比如人工神经网络(artificial neural network,ANN)、自回归(autoregressive,AR)、高斯过程回归(Gaussian process regression) [85-86]等.文献[87]利用粒子群优化算法改进的AR模型进行在线预测.AR模型的计算简单,但预测结果没有不确定性结果表达式.文献[88]提出了基于差分整合移动平均自回归(autoregressive integrated moving average,ARIMA)模型的RUL预测方法,然而ARIMA模型要求时序数据的平稳性,对电池运行工况有较高要求.文献[89]使用动态递归神经网络(dynamically driven recurrent network,DDRN)来降低网络结构的复杂性,提升算法鲁棒性,然而DDRN容易出现梯度消失的问题.除了数据驱动法本身的问题,直接数据驱动法在RUL预测方面还存在以下问题: ...
Lithium-ion batteries remaining useful life prediction based on a mixture of empirical mode decomposition and ARIMA model
1
2016
... 现有的方法同样包括神经网络、回归算法以及其他方法,比如人工神经网络(artificial neural network,ANN)、自回归(autoregressive,AR)、高斯过程回归(Gaussian process regression) [85-86]等.文献[87]利用粒子群优化算法改进的AR模型进行在线预测.AR模型的计算简单,但预测结果没有不确定性结果表达式.文献[88]提出了基于差分整合移动平均自回归(autoregressive integrated moving average,ARIMA)模型的RUL预测方法,然而ARIMA模型要求时序数据的平稳性,对电池运行工况有较高要求.文献[89]使用动态递归神经网络(dynamically driven recurrent network,DDRN)来降低网络结构的复杂性,提升算法鲁棒性,然而DDRN容易出现梯度消失的问题.除了数据驱动法本身的问题,直接数据驱动法在RUL预测方面还存在以下问题: ...
State of charge and state of health estimation for lithium batteries using recurrent neural networks
1
2017
... 现有的方法同样包括神经网络、回归算法以及其他方法,比如人工神经网络(artificial neural network,ANN)、自回归(autoregressive,AR)、高斯过程回归(Gaussian process regression) [85-86]等.文献[87]利用粒子群优化算法改进的AR模型进行在线预测.AR模型的计算简单,但预测结果没有不确定性结果表达式.文献[88]提出了基于差分整合移动平均自回归(autoregressive integrated moving average,ARIMA)模型的RUL预测方法,然而ARIMA模型要求时序数据的平稳性,对电池运行工况有较高要求.文献[89]使用动态递归神经网络(dynamically driven recurrent network,DDRN)来降低网络结构的复杂性,提升算法鲁棒性,然而DDRN容易出现梯度消失的问题.除了数据驱动法本身的问题,直接数据驱动法在RUL预测方面还存在以下问题: ...
Comparative analysis of features for determining state of health in lithium-ion batteries
1
2013
... 1)一次特征.指直接从曲线中提取的特征,比如充放电电流、电压、温度曲线某段时间变化量或某变化量所需时间.文献[90]提取了恒流(constant current,CC)充电时间与恒压(constant voltage,CV)充电时间作为HF.文献[91]选择放电过程中相同时间区间内的电压变化与放电过程中相同温度变化所需时间来预测电池RUL.文献[92]提取了放电过程中电压从3.9 V下降至3.5 V的时间及温度上升至最大值所需时间.文献[93]提出了15个和电池充放电过程中电流、电压、温度曲线相关的特征. ...
A novel health index for battery RUL degradation modeling and prognostics
1
2019
... 1)一次特征.指直接从曲线中提取的特征,比如充放电电流、电压、温度曲线某段时间变化量或某变化量所需时间.文献[90]提取了恒流(constant current,CC)充电时间与恒压(constant voltage,CV)充电时间作为HF.文献[91]选择放电过程中相同时间区间内的电压变化与放电过程中相同温度变化所需时间来预测电池RUL.文献[92]提取了放电过程中电压从3.9 V下降至3.5 V的时间及温度上升至最大值所需时间.文献[93]提出了15个和电池充放电过程中电流、电压、温度曲线相关的特征. ...
SOH and RUL prediction of lithium-ion batteries based on gaussian process regression with indirect health indicators
1
2020
... 1)一次特征.指直接从曲线中提取的特征,比如充放电电流、电压、温度曲线某段时间变化量或某变化量所需时间.文献[90]提取了恒流(constant current,CC)充电时间与恒压(constant voltage,CV)充电时间作为HF.文献[91]选择放电过程中相同时间区间内的电压变化与放电过程中相同温度变化所需时间来预测电池RUL.文献[92]提取了放电过程中电压从3.9 V下降至3.5 V的时间及温度上升至最大值所需时间.文献[93]提出了15个和电池充放电过程中电流、电压、温度曲线相关的特征. ...
Remaining useful life prediction for lithium-ion battery:a deep learning approach
1
2018
... 1)一次特征.指直接从曲线中提取的特征,比如充放电电流、电压、温度曲线某段时间变化量或某变化量所需时间.文献[90]提取了恒流(constant current,CC)充电时间与恒压(constant voltage,CV)充电时间作为HF.文献[91]选择放电过程中相同时间区间内的电压变化与放电过程中相同温度变化所需时间来预测电池RUL.文献[92]提取了放电过程中电压从3.9 V下降至3.5 V的时间及温度上升至最大值所需时间.文献[93]提出了15个和电池充放电过程中电流、电压、温度曲线相关的特征. ...
On-line life cycle health assessment for lithium-ion battery in electric vehicles
1
2018
... 2)二次特征.指需要做积分等二次处理的特征,如dQ/dV等.文献[94]提出将dQ/dV与dV/dQ作为HF.文献[95]提出可将放电过程电压特性曲线初始最大斜率、CV充电过程中电流曲线的最大斜率、电流曲线与横轴围成面积作为HF. ...
基于时空分布映射的大规模电池健康状态研究
1
2022
... 2)二次特征.指需要做积分等二次处理的特征,如dQ/dV等.文献[94]提出将dQ/dV与dV/dQ作为HF.文献[95]提出可将放电过程电压特性曲线初始最大斜率、CV充电过程中电流曲线的最大斜率、电流曲线与横轴围成面积作为HF. ...
基于时空分布映射的大规模电池健康状态研究
1
2022
... 2)二次特征.指需要做积分等二次处理的特征,如dQ/dV等.文献[94]提出将dQ/dV与dV/dQ作为HF.文献[95]提出可将放电过程电压特性曲线初始最大斜率、CV充电过程中电流曲线的最大斜率、电流曲线与横轴围成面积作为HF. ...
Remaining useful life prediction of battery using a novel indicator and framework with fractional grey model and unscented particle filter
1
2020
... 3)其他.文献[96]使用了一种放电电压的小波包能量熵作为HF.获取HF后,基于Pearson系数、Spearman系数、灰度关联分析等相关性分析方法,对HF与容量的相关性进行分析,选取相关性满足一定标准的HF或者基于主成分分析(principal component analysis,PCA)对众多HF进行降维,作为数据驱动模型的特征输入,即可预测RUL[97-98]. ...
State-of-health estimation and remaining-useful-life prediction for lithium-ion battery using a hybrid data-driven method
1
2020
... 3)其他.文献[96]使用了一种放电电压的小波包能量熵作为HF.获取HF后,基于Pearson系数、Spearman系数、灰度关联分析等相关性分析方法,对HF与容量的相关性进行分析,选取相关性满足一定标准的HF或者基于主成分分析(principal component analysis,PCA)对众多HF进行降维,作为数据驱动模型的特征输入,即可预测RUL[97-98]. ...
Battery remaining useful life prediction algorithm based on support vector regression and unscented particle filter
1
2016
... 3)其他.文献[96]使用了一种放电电压的小波包能量熵作为HF.获取HF后,基于Pearson系数、Spearman系数、灰度关联分析等相关性分析方法,对HF与容量的相关性进行分析,选取相关性满足一定标准的HF或者基于主成分分析(principal component analysis,PCA)对众多HF进行降维,作为数据驱动模型的特征输入,即可预测RUL[97-98]. ...
基于 AFFDRLS-AHIF 对动力锂离子电池单体SOC 估计
1
2020
... 第一类融合类算法是模型和数据驱动法融合.文献[99]提出了一种基于支持向量回归和无迹粒子滤波融合的算法,使用支持向量回归在重采样阶段获取重新赋权的粒子,解决了粒子贫化的问题,提高了预测性能.文献[100]使用神经网络来分析OCV和SOC之间的非线性关系,并使用改进UKF来估算锂离子电池SOC,结果表明相比于单一UKF方法,该方法的估算精度更高. ...
基于 AFFDRLS-AHIF 对动力锂离子电池单体SOC 估计
1
2020
... 第一类融合类算法是模型和数据驱动法融合.文献[99]提出了一种基于支持向量回归和无迹粒子滤波融合的算法,使用支持向量回归在重采样阶段获取重新赋权的粒子,解决了粒子贫化的问题,提高了预测性能.文献[100]使用神经网络来分析OCV和SOC之间的非线性关系,并使用改进UKF来估算锂离子电池SOC,结果表明相比于单一UKF方法,该方法的估算精度更高. ...
Battery prognostics
1
2003
... 第一类融合类算法是模型和数据驱动法融合.文献[99]提出了一种基于支持向量回归和无迹粒子滤波融合的算法,使用支持向量回归在重采样阶段获取重新赋权的粒子,解决了粒子贫化的问题,提高了预测性能.文献[100]使用神经网络来分析OCV和SOC之间的非线性关系,并使用改进UKF来估算锂离子电池SOC,结果表明相比于单一UKF方法,该方法的估算精度更高. ...
利用信息融合技术的储能锂离子电池组 SOC 估算
1
2016
... 第二类融合型算法结合多种不同的数据驱动方法,通过加权或其他融合方式,提高预测结果的稳定性.例如,文献[101]根据电池运行模式将OCV-SOC曲线划分为不同区间,同时结合ANN 及模糊逻辑数据信息处理技术实时修正模型参数,进而取得了较好的SOC估算效果.融合方法能够较好地提升寿命预测的性能,但是目前仍存在计算复杂度高、不确定性融合等挑战.常见锂离子电池RUL预测方法的优缺点比较如表3所示. ...
利用信息融合技术的储能锂离子电池组 SOC 估算
1
2016
... 第二类融合型算法结合多种不同的数据驱动方法,通过加权或其他融合方式,提高预测结果的稳定性.例如,文献[101]根据电池运行模式将OCV-SOC曲线划分为不同区间,同时结合ANN 及模糊逻辑数据信息处理技术实时修正模型参数,进而取得了较好的SOC估算效果.融合方法能够较好地提升寿命预测的性能,但是目前仍存在计算复杂度高、不确定性融合等挑战.常见锂离子电池RUL预测方法的优缺点比较如表3所示. ...