0 引言
快离子是磁约束燃烧等离子体的重要组成部分,是加热等离子体和维持聚变燃烧的重要能量来源。此外,快离子还是托卡马克等离子体中动量和电流的重要来源[1 ] 。在未来的磁约束聚变反应堆中,快离子的主要来源是聚变反应产生的能量为3.5 Mev的α 粒子。由于快离子的温度远高于热离子,快离子的动理学特性与热离子有很大差异。因此,对装置内的快离子进行诊断是十分重要且具有挑战性的[2 ] 。
相干汤姆逊散射(collective Thomson scattering,CTS)物理模型的建立以及相应的散射频谱数值计算是设计CTS诊断系统的基础。因此,有必要发展出完备的CTS散射模型代码以支持CTS诊断的开展和诊断系统的设计[3 ] 。目前,国内外主流的CTS模型主要是静电模型和全电磁模型。在20世纪80年代,Vahala、Hughes等[4 -5 ] 基于这种静电模型开展了详细的散射频谱理论计算,验证了CTS诊断用于测量α 粒子速度分布函数的可行性。后续的研究发现,当等离子体扰动波矢量与磁场之间接近于垂直时,上述的静电模型不再准确,Aamodt等[6 ] 研究指出,此时需要对等离子体介电函数进行电磁处理。研究中还发现,在一些特定的等离子体参数条件下,静电模型中散射仅来自电子密度扰动的假设是不正确的。为此,研究者[6 -8 ] 进一步发展了全电磁模型。静电模型仅考虑了电子密度的扰动对CTS信号的贡献,而全电磁模型考虑了电场、磁场、电子密度和电流密度扰动对CTS信号的贡献[9 ] 。从动理学弗拉索夫方程的角度出发,冷、热等离子体的划分是按其是否受有限温度效应的影响,流体和非流体等离子体的划分是按波的相速度是否远大于粒子的热速度[10 ] 。在CTS散射实验中,入射光和散射光的频率足够高,因此等离子体可以被视为这些波的冷源。然而,观察到的扰动的相速度通常与电子的热速度相同或更小,并且可能还必须考虑粒子的非关联运动,因此不可将扰动视为冷集体振荡。这里,冷流体模型不能保证准确,这是因为冷流体模型是由动理学模型基于冷集体振荡假设所推导出来的,它无法体现粒子的非关联运动也无法体现扰动波矢受温度的有限影响,因此Bindslev[7 ] 指出应该回归更加基本的动理学理论。
本文通过改进等离子体介电性质和考虑更全面的电磁效应发展了一套全电磁模型CTS频谱数值计算代码,基于全电磁模型,比较了全电磁模型与静电模型的共性与差异,优化了HL-2A装置CTS系统的参数,为CTS诊断系统的设计和CTS诊断的开展提供数值工具和理论基础。
1 CTS全电磁模型
1.1 CTS全电磁动理学模型
CTS的原理是将入射的电磁波束(通常在毫米波范围内)散射到电子分布中的微观集体涨落上并发出散射辐射,这些涨落是由运动离子的德拜屏蔽引起的。通过设置接收天线的角度,可以对某个特定空间位置发出的散射辐射进行接收,这就确定了散射的几何结构。要实现这种电子的微观集体涨落,需要入射波和散射几何结构满足Salpeter准则[9 ] :
α = ( k λ D ) - 1 > 1 (1)
式中:α 为Salpeter参数;k -1 ;λ D
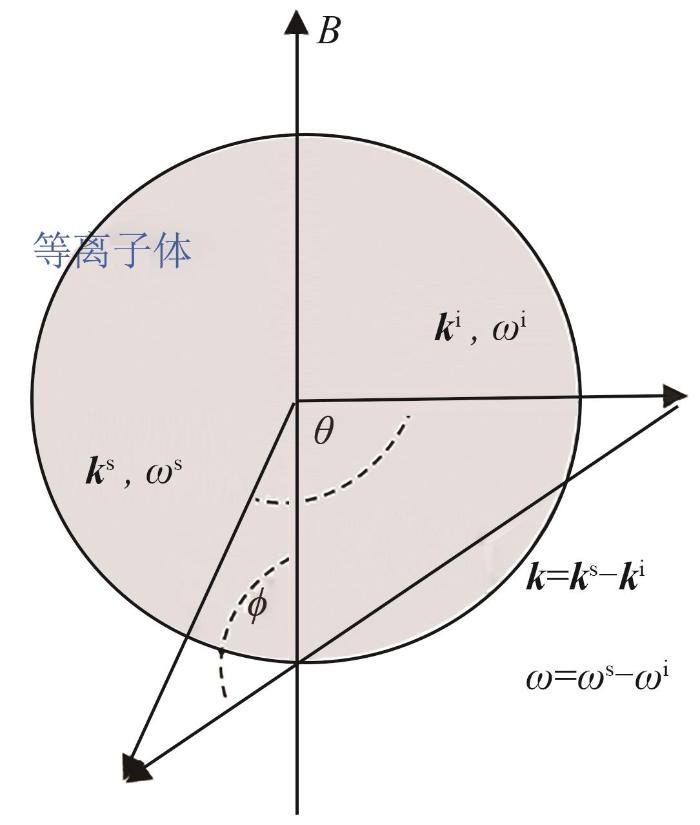
扰动波矢具体可由散射几何来定义,如图1 所示。其中 k i 、ω i , k s 、ω s , k ω 分别为入射波束、散射波束、扰动波束的波矢和角频率,单位分别为m-1 和rad/s; B θ 为入射波矢与散射波矢之间的夹角;ϕ 为磁场与扰动波矢之间的夹角。
图1
图1
CTS散射几何结构图
Fig. 1
CTS scattering geometric structure diagram
非碰撞的等离子体的微观分布函数f M [7 ] :
( ∂ t + v ⋅ ∂ r + F M ⋅ ∂ p ) f M = 0 (2)
F M = q ( E M + v × B M ) (3)
式中: v q 为粒子的电荷,C; t p r E M B M F M
f = f M (4)
f ˜ = f M - f (5)
由此,可以推导出接收器接收的散射功率密度谱[7 ] :
∂ P s ∂ ω s = P i O b ( λ 0 i ) 2 r e 2 1 2 π ∑ α ∑ ( a ) (6)
∑ ( a ) = ∑ α β ∑ α β ( a ) , α , β = n , j , E , B (7)
式中:n 为等离子体电子密度,m-3 ;j 为电流密度,A/m2 ;E 为电场强度,V/m;B 为磁场强度,T;P i 、P s 分别为入射和散射探测光束的功率,W;λ 0 i r e 为经典电子半径,m;∑ α β ( a ) 为 a 的热运动驱动的等离子体扰动在不同场和流体变量中的散射函数;∑ ( a ) 为 O b 为光束交叠,m3 ,O b 的计算公式如下:
O b = ∫ I i I s d V (8)
I = P ∫ P d A (9)
式中:I i I s I 为束波的归一化强度;P 为波束截面上单位面积内的功率,W;V 为光束交叠的体积,m3 ;A 为波束截面面积,m2 。
∑ α β ( a ) = C G ^ i ( α ) α ˜ i ( a ) β ˜ j ( a ) G ^ j ( β ) * (10)
C = ( ω i ω s ) 2 ω p e 4 1 ζ i ζ s (11)
式中:C 为散射函数的计算系数;ω pe 为电子等离子体频率,rad/s;ω i 和ω s 分别为入射波和散射波频率,rad/s;ζ i ζ s α ˜ i ( a ) 、 β ˜ j ( a ) a 的扰动量;G ^ i ( α ) G ^ j ( β ) α 和β 的介电耦合算符;上标*表示复共轭。
ζ i = N i k ^ i - R e { ( k ^ i ⋅ e i ) ( e i ) * } (12)
e i = E i E i (13)
N i = k i c ω i (14)
k ^ i = k i k i (15)
式中:N i e i E i k ^ i c 为真空光速,m/s。
α ˜ i ( a ) β ˜ j ( a ) S ^ j ˜ k ( a 0 ) j ˜ k ' ( a 0 )
α ˜ i ( a ) β ˜ j ( a ) = S ^ i k ( α a ) j ˜ k ( a 0 ) j ˜ k ' ( a 0 ) S ^ i ' k ' ( β a ) * (16)
式中:S ^ i k ( α a ) S ^ i ' k ' ( β a ) α 和β 的扰动算符矩阵的不同矩阵元;j ˜ k ( a 0 ) j ˜ k ' ( a 0 )
扰动算符量化了等离子体对未屏蔽电流扰动的响应,其表达式[7 ] 如下:
S ^ i k ( E a ) = Λ i k - 1 - i ω ε 0 (17)
S ^ i k ( B a ) = k ω σ i j l k ^ j S ^ l k ( E ) (18)
S ^ i k ( j i ) = - χ i j ( e ) Λ j k - 1 (19)
S ^ i k ( j e ) = S ^ i k ( j i ) + δ i k (20)
式中:S ^ i k ( E a ) S ^ i k ( B a ) S ^ i k ( j i ) S ^ i k ( j e ) S ^ l k ( E ) Λ i k - 1 Λ j k - 1 σ i j l ε 0 k ^ j χ i j ( e ) δ i k
j ˜ k ( a 0 ) j ˜ k ' ( a 0 ) a 未扰动的宏观分布函数表示为:
j ˜ k ( a 0 ) j ˜ k ' ( a 0 ) = ( 2 π ) 2 m a q a 2 k ∥ ∫ C k k ' d v ⊥ v ⊥ (21)
C k k ' = ∑ l = - ∞ ∞ c k l c k ' l * f ( a 0 ) ( v ⊥ , v ∥ ) (22)
c l = l ω c a k ⊥ J l ( k ⊥ ρ ) - i v ⊥ J l ' ( k ⊥ ρ ) v ∥ J l ( k ⊥ ρ ) (23)
v ∥ = ω - l ω c a k ∥ (24)
式中:ma 为粒子a 的质量,kg;qa 为粒子a 的电荷,C;C k k ' c l c k l c k ' l c l ∥ 和 ⊥ B (0) 平行和垂直的矢量分量;l 为求和的阶数;v ⊥ v ∥ k ⊥ k ∥ -1 ;B (0) 为静态磁场强度,T;f ( a 0 ) J l l 的第一类贝塞尔函数,J l ' ρ ω c a
G ^ E , B , j , n }变量的扰动之间的相互作用,以及与散射波的耦合,可被入射波和散射波[7 ] 表示如下:
G ^ ( n ) = ( e i s ) * χ i l s e l i (25)
G ^ k ( B ) = - ( e i s ) * χ i j s ε j m k i ω i ε 0 q e χ m l i e l i (26)
G ^ k ( j ) = ( e i s ) * 1 q e ( χ i j s σ j m k σ m n l k n i ω i + X i k l s 1 c ) e l i (27)
G ^ k ( E ) = - ( e i s ) * ( χ i k s i ε 0 q e k j i + X i j k s i ω i ε 0 c q e ) χ j l i e l i (28)
式中:G ^ ( n ) G ^ k ( B ) G ^ k ( j ) G ^ k ( E ) e i s e l i k n i k j i -1 ;χ i l s χ i j s χ i k s χ j l i χ m l i σ j m k σ m n l q e X i k l s X i j k s
1.2 磁化等离子体的介电性质
在相干汤姆逊散射过程中,扰动电场和扰动电流满足方程[10 ] :
Λ i j E ˜ j ( k , ω ) = - i ω ε 0 ∑ a j ˜ i ( a 0 ) ( k , ω ) (29)
Λ i j = ε i j + N 2 { k ^ i k ^ j - δ i j } (30)
ε i j = δ i j + ∑ a χ i j ( a ) (31)
式中:Λ i j j ˜ i ( a 0 ) 2 ;E ˜ j ε i j N 为扰动波的折射率;k ^ i k ^ j δ i j χ i j ( a )
从式(19)和式(31)可以看出,等离子体介电张量的正确计算是计算散射频谱的关键。在早期的一些理论中,采用冷等离子介电张量,但这种冷等离子体的近似无法正确描述散射过程中由粒子热运动产生的空间色散[7 ] 。后续的一些研究表明,热等离子体和相对论等离子体是更完备的近似[8 ] 。本文在处理由扰动量产生的散射过程中均采用热等离子体的近似。
在入射波和散射波的色散关系以及耦合算符的计算中也需要考虑等离子体的介电性质。由于入射波和散射波是高频的电磁波且耦合算符仅与入射波和散射波有关,这时冷等离子体的近似是恰当的。在确定了等离子体介电性质后,散射波的三阶伪张量的矩阵元[10 ] 便可被表示为
X h l k s = c k j s ω s χ h i s Γ i j a b - 1 ( δ a k δ b l + δ a l δ b k ) (32)
式中:Γ i j a b - 1 7 ]中定义的四阶矩阵的逆矩阵的矩阵元;δ a k δ b l δ a l δ b k χ h i s k j s -1 。
2 CTS全电磁模型散射频谱计算
2.1 全电磁模型与静电模型的对比验证
在大多数CTS散射频谱的计算算例中,全电磁模型与静电模型计算的散射频谱基本一致,这是因为在大多数情况下,密度扰动造成的散射功率远大于其他扰动量产生的散射功率。
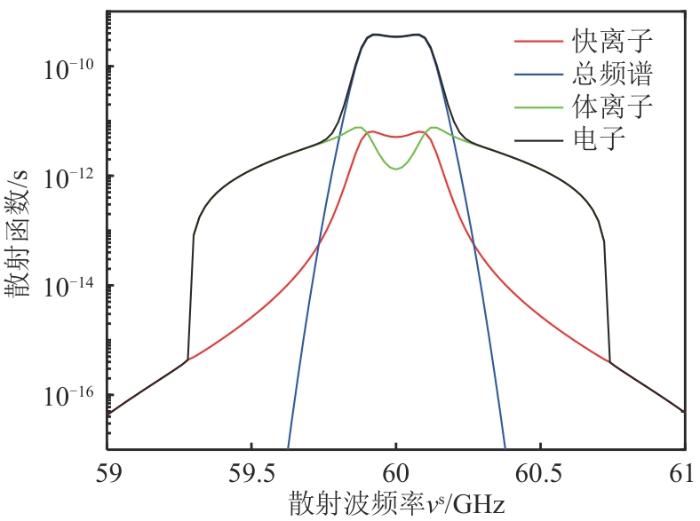
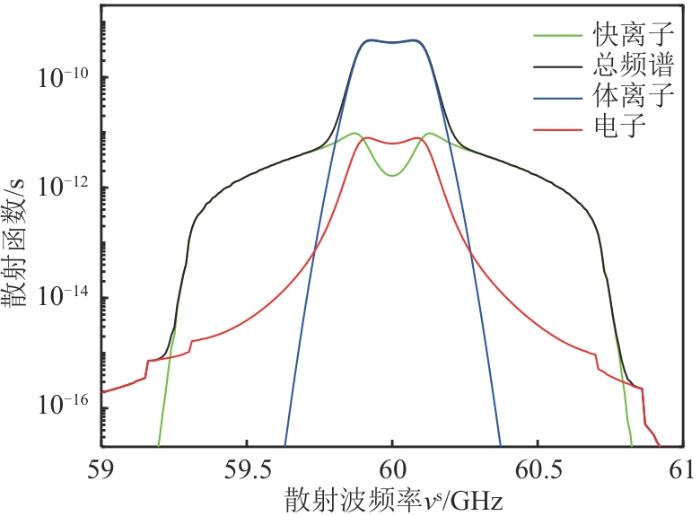
为保证本文全电磁模型散射频谱计算代码的准确性与可靠性,分别利用静电模型和全电磁模型计算散射函数进行对比验证。输入参数选取了国际热核聚变实验反应堆(international thermonuclear experimental reactor,ITER)装置设计的CTS诊断系统及等离子体参数[11 -13 ] ,如表1 所示。其中,快离子为α 粒子,且服从初始温度为3.5 MeV的经典慢化分布。
2种模型计算的散射频谱如图2 和图3 所示。可以看出,在ITER装置的等离子体参数下,2种模型计算的CTS散射频谱几乎完全一致,这说明本文采用的全电磁模型散射频谱计算代码是正确的。
图2
图2
基于ITER装置参数的静电模型散射函数
Fig. 2
Scattering function of the electrostatic model based on ITER device parameters
图3
图3
基于ITER装置参数的全电磁模型散射函数
Fig. 3
Scattering function of the full electromagnetic model based on ITER device parameters
2.2 CTS全电磁模型
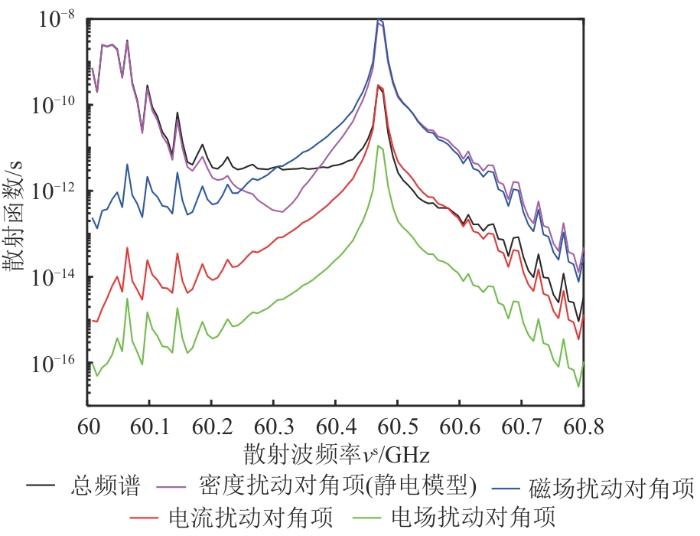
虽然在大多数情况下,密度扰动产生的散射功率远大于其他扰动量产生的散射功率,但当扰动波矢与磁场间的夹角ϕ [14 ] 结构和离子回旋结构会在趋近于90°时出现,这是因为在ϕ k ∥ [15 ] 。这种结构对于CTS系统诊断聚变堆燃料比是必不可少的。因此,有必要对趋近于90°时的CTS全电磁模型频谱结构进行研究和分析。
仍以表1 中ITER装置D-T等离子体的参数为基础,更改ϕ 7 ]表明这种参数下静电结果和全电磁结果会有较大差别。本文的计算结果如图4 所示。
图4
图4
全电磁模型散射函数及其不同扰动量的散射函数分量
Fig. 4
scattering function of the full electromagnetic model and its scattering function components for different fluctuations
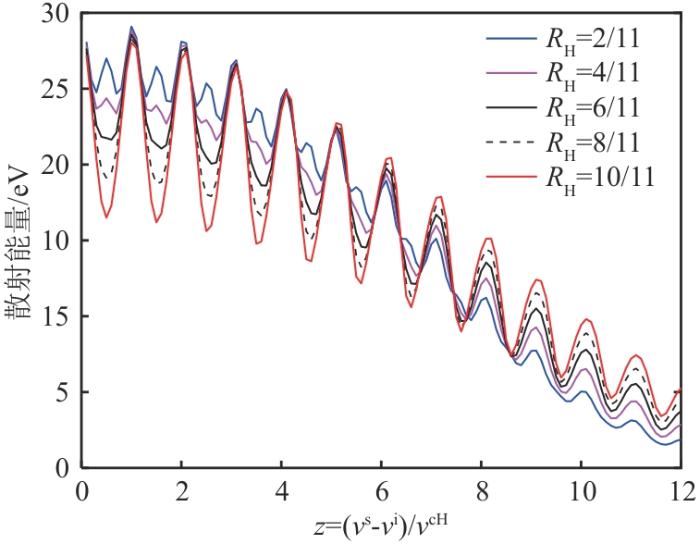
从图4 中可以看出,密度分量不再完全成为总散射函数的主要成分。在散射波频率小于60.2 GHz时,密度扰动占主要成分;在60.2~60.4 GHz,多种成分一起构成了散射函数;在大于60.4 GHz后,电流密度的扰动占散射函数的主要成分,散射函数的峰值在60.47 GHz处,此处静电模型与全电磁模型的散射函数强度上相差接近1个数量级。由此可见,只有全电磁模型可以正确处理这种特殊的CTS频谱结构。图4 中低频率出现的频谱振荡情况是源于离子-伯恩斯坦波模式,而频谱峰值出现在60.47 GHz处是源于快磁声波[7 ] 。CTS频谱中的离子-伯恩斯坦波结构及离子回旋结构是诊断托卡马克装置及聚变堆的离子比例的基础,图5 为全电磁模型CTS散射功率谱随H离子含量变化而产生的不同结构,参数来源于TEXTOR装置CTS系统[15 ] ,如表2 所示,其中R H = n H / n e n H -3 ,离子种类为D-H等离子体,图5 横坐标Z = v s - v i / v c H v i v s v c H
图5
图5
不同H离子含量的CTS散射能量谱
Fig. 5
CTS spectra power density with different H ion contents
从图5 中可以看出,CTS频谱中的离子-伯恩斯坦波结构及离子回旋结构对H离子浓度的敏感性相对较高,类似的结果在2011年TEXTOR装置利用CTS观测离子伯恩斯坦波的实验与模拟中也被验证[14 -15 ] 。这说明本文采用的全电磁模型代码可以作为聚变装置诊断离子比例的基础。
3 HL-2A装置全电磁模型CTS频谱
3.1 HL-2A装置 CTS系统简介
目前国内的托卡马克上尚未系统性地开展CTS诊断研究,一定程度上不利于相关技术[16 ] 的发展。HL-2A装置上建有完备的中性束注入(neutral beam injection heating,NBI)系统和电子回旋加热(electron cyclotron resonance heating,ECRH)系统,能为国内CTS诊断研究的开展提供较好的平台支撑。因此,亟须研究HL-2A装置上的散射频谱特性。
HL-2A装置是由核工业西南物理研究院建造的磁约束核聚变装置[17 -18 ] ,同时也是我国第一个具有偏滤器位形的大型托卡马克装置。HL-2A装置上建有5 MW ECRH系统。该系统主要包含6支0.5 MW/68 GHz/1 s回旋管和2支1 MW/140 GHz/3 s回旋管,其还可以运行在0.5 MW/105 GHz/0.1 s的输出模式下[19 -20 ] 。因此,如果基于HL-2A装置的ECRH系统搭建CTS诊断系统,探测波频率可以选择的有68 GHz、105 GHz 和140 GHz。当频率选择为68 GHz时,且纵场为 1.84~2.43 T时,2次谐波共振层位于高场侧,入射的微波在经过测量位置后可能会被等离子体吸收,此时接收波束也可能穿过2次谐波共振层,导致较强的电子回旋辐射被散射信号接收系统收集,这会进一步减小信噪比。故在纵场为2 T附近时,不宜选用68 GHz作为探测波频率。本文研究的HL-2A装置的CTS诊断系统将基于105 GHz和140 GHz两种频率进行设计。
3.2 HL-2A装置全电磁模型CTS频谱特性分析
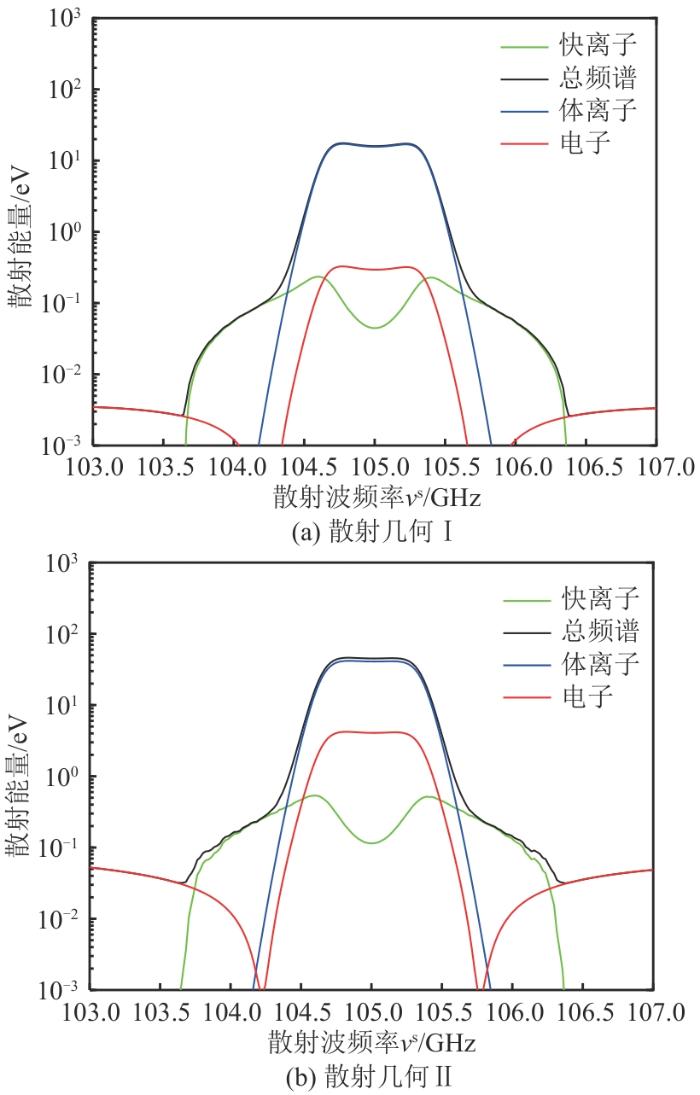
本文分别研究HL-2A装置上2种散射几何和105、140 GHz探测波频率的CTS散射能量谱,以优化CTS诊断系统参数。这2种散射几何分别为Ⅰ(θ ϕ θ ϕ [21 ] 。散射能量谱的计算输入参数如表3 所示,主离子和快离子均为氘离子。2种探测波频率下2种散射几何的计算结果分别如图6 和图7 所示。可以看出,105 GHz的快离子诊断区域相对较宽,且散射能量更大,这意味着更好的信噪比,故探测波频率应选择105 GHz。在105 GHz的探测波频率下,2种散射几何的快离子诊断区域相差不大,但散射几何Ⅱ的散射能量更大。同时,散射几何Ⅰ对快离子平行于磁场方向上速度具有高分辨率,这有利于后续利用CTS系统诊断快离子分布的各向异性。
图6
图6
105 GHz CTS 诊断在2种散射几何下的散射能量谱
Fig. 6
105 GHz CTS diagnostics spectra power density under scattering geometries
图7
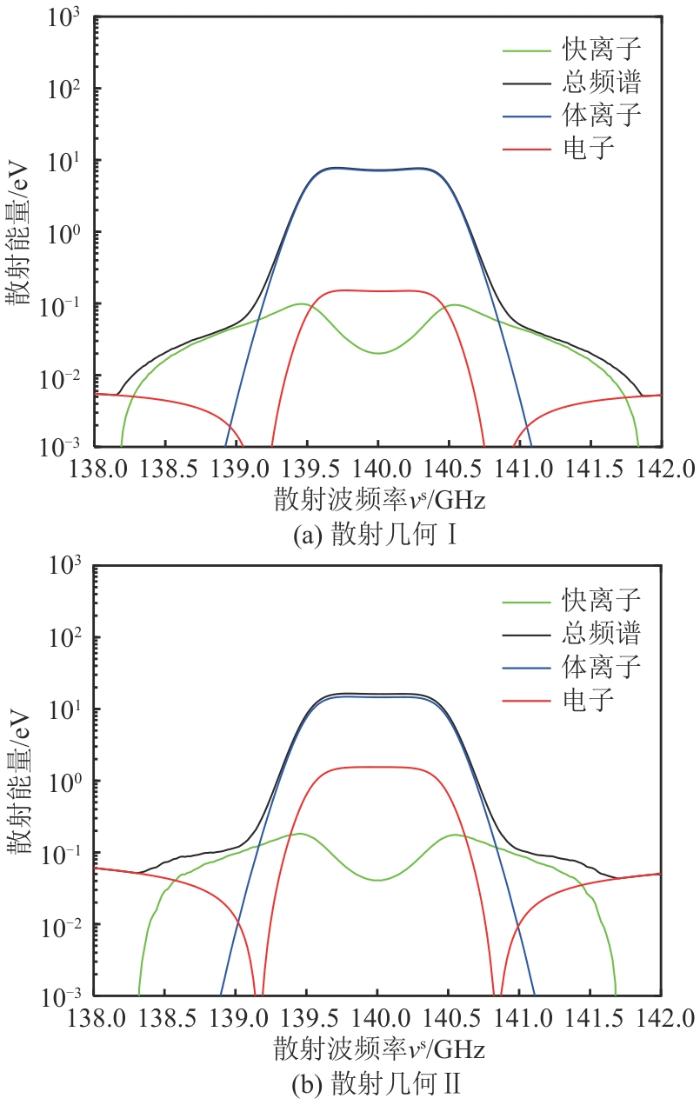
图7
140 GHz CTS 诊断在2种散射几何下的散射能量谱
Fig. 7
140 GHz CTS diagnostics spectra power density under scattering geometries
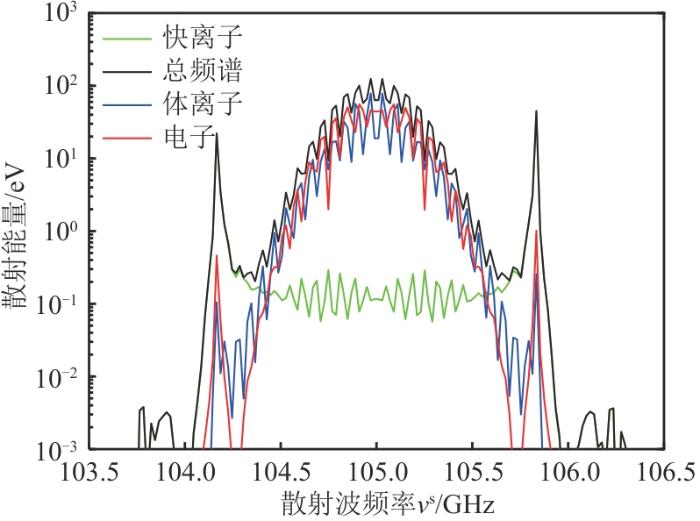
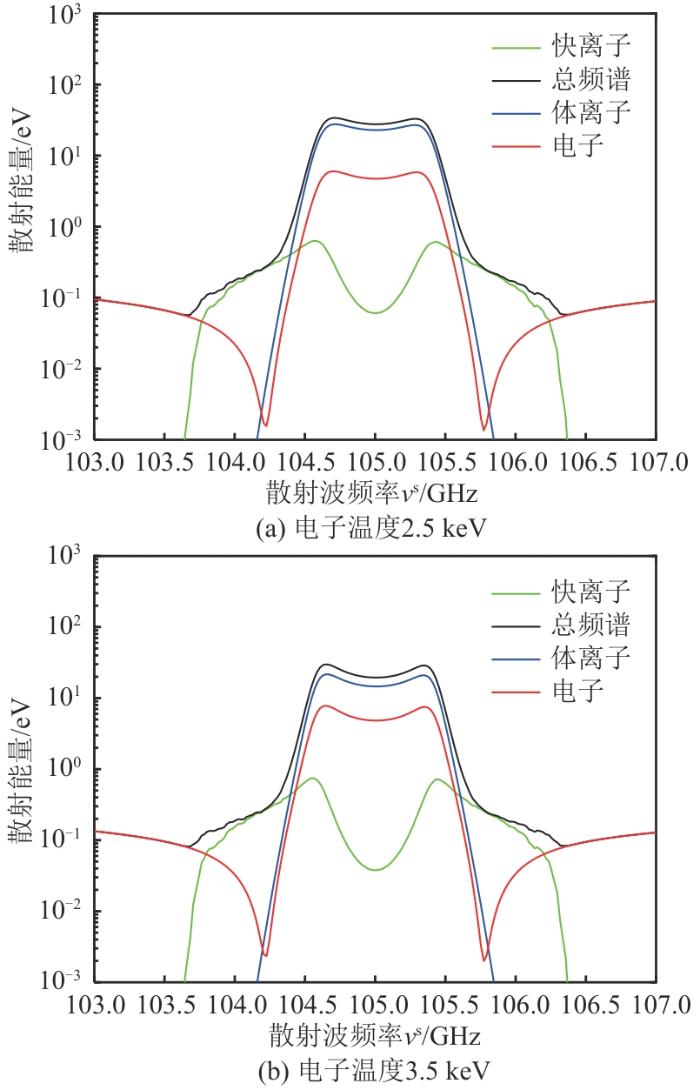
综合考虑,选择105 GHz CTS诊断系统在散射几何Ⅱ下对表3 给定参数进行常规快离子诊断,在散射几何Ⅰ下进行快离子各向异性的诊断[22 -26 ] 。HL-2A装置的CTS诊断系统同样具有诊断离子含量的能力。更改ϕ 图8 所示。这说明CTS诊断系统具有在HL-2A上诊断离子比例的潜力。此外,温度对频谱的影响也不可忽视。由图6 可见,在105 GHz散射几何Ⅱ的情况下,电子频谱是影响快离子诊断区间的关键,故提升电子温度会提升电子频谱能量及降低快离子诊断区间宽度。如图9 所示,提升电子温度分别为2.5 keV和3.5 keV,电子的频谱能量逐渐变强并导致快离子诊断区间变窄。
图8
图8
HL-2A装置CTS散射能量谱的离子-伯恩斯坦波结构
Fig. 8
Ion-Bernstein wave structure in the CTS spectra power density of the HL-2A device
图9
图9
105 GHz CTS 诊断在2种电子温度下的散射能量谱
Fig. 9
Spectra power density of 105 GHz CTS diagnostic at two electron temperatures
4 结论
基于CTS全电磁动理学模型开发了一套CTS频谱数值计算代码,分别利用静电模型和全电磁模型计算散射函数进行对比验证,得到以下结论:
1)ITER装置参数下全电磁模型计算的CTS频谱与静电模型计算结果一致,验证了代码的可靠性。
2)全电磁模型代码相比静电模型更加全面,同时全电磁模型CTS频谱中会出现离子-伯恩斯坦波与离子回旋波结构,这说明全电磁模型具有成为CTS诊断离子比例的基础工具的潜力。
3)通过HL-2A装置开展的全电磁模型CTS频谱研究,优化出了一套适合于HL-2A装置的CTS诊断系统参数,证明了HL-2A装置有能力基于CTS系统开展高效的快离子和离子-伯恩斯坦波诊断。
CTS全电磁模型在诊断离子比例、等离子体转动速度和快离子速度分布等方面可以发挥重要作用。未来将基于此全电磁模型代码,结合国内外其他装置发展更多研究方向。
参考文献
View Option
[1]
MOSEEV D SALEWSKI M GARCIA-MUOZ M et al Recent progress in fast-ion diagnostics for magnetically confined plasmas
[J].Reviews of Modern Plasma Physics ,2018 ,2 (1 ):7 . doi:10.1007/s41614-018-0019-4
[本文引用: 1]
[2]
NIELSEN S K MICHELSEN P K HANSEN S K et al Recent development of collective Thomson scattering for magnetically confined fusion plasmas
[J].Physica Scripta ,2017 ,92 (2 ):024001 . doi:10.1088/1402-4896/92/2/024001
[本文引用: 1]
[3]
VAHALA L VAHALA G SIGMAR D J Effects of alpha particles on the scattering function in CO2 laser scattering
[J].Nuclear Fusion ,1986 ,26 (1 ):51 -60 . doi:10.1088/0029-5515/26/1/005
[本文引用: 1]
[4]
VAHALA L VAHALA G SIGMAR D J Effect of electrostatic scattering parameters on the direct detection of fusion alphas
[J].Nuclear Fusion ,1988 ,28 (9 ):1595 -1602 . doi:10.1088/0029-5515/28/9/008
[本文引用: 1]
[5]
HUGHES T P SMITH S R P Calculations of Thomson scattering functions for alpha particle diagnostics in JET plasmas
[J].Nuclear Fusion ,1988 ,28 (8 ):1451 -1457 . doi:10.1088/0029-5515/28/8/012
[本文引用: 1]
[6]
AAMODT R E RUSSELL D A Alpha particle detection by electromagnetic scattering off of plasma fluctuations
[J].Nuclear Fusion ,1992 ,32 (5 ):745 -755 . doi:10.1088/0029-5515/32/5/i03
[本文引用: 2]
[7]
BINDSLEV H A quantitative study of scattering from electromagnetic fluctuations in plasmas
[J].Journal of Atmospheric and Terrestrial Physics ,1996 ,58 (8/9 ):983 -989 . doi:10.1016/0021-9169(95)00129-8
[本文引用: 9]
[8]
NIELSEN S K BINDSLEV H PORTE L et al Temporal evolution of confined fast-ion velocity distributions measured by collective Thomson scattering in TEXTOR
[J].Physical Review E ,2008 ,77 (1 ):016407 . doi:10.1103/physreve.77.016407
[本文引用: 2]
[11]
KORSHOLM S B GONÇALVES B GUTIERREZ H E et al Design and development of the ITER CTS diagnostic
[J].EPJ Web of Conferences ,2019 ,203 :03002 . doi:10.1051/epjconf/201920303002
[本文引用: 1]
[12]
RASMUSSEN J STEJNER M JENSEN T et al Inference of α -particle density profiles from ITER collective Thomson scattering
[J].Nuclear Fusion ,2019 ,59 (9 ):096051 . doi:10.1088/1741-4326/ab2f50
[13]
KORSHOLM S B CHAMBON A GONÇALVES B et al ITER collective Thomson scattering:preparing to diagnose fusion-born alpha particles (invited)
[J].Review of Scientific Instruments ,2022 ,93 (10 ):103539 . doi:10.1063/5.0101867
[本文引用: 1]
[14]
KORSHOLM S B STEJNER M BINDSLEV H et al Measurements of intrinsic ion Bernstein waves in a tokamak by collective Thomson scattering
[J].Physical Review Letters ,2011 ,106 (16 ):165004 . doi:10.1103/physrevlett.106.165004
[本文引用: 2]
[15]
STEJNER M NIELSEN S K BINDSLEV H et al Principles of fuel ion ratio measurements in fusion plasmas by collective Thomson scattering
[J].Plasma Physics and Controlled Fusion ,2011 ,53 (6 ):065020 . doi:10.1088/0741-3335/53/6/065020
[本文引用: 3]
[16]
张家龙 ,宋彭 ,瞿体明 磁约束可控核聚变装置的磁体系统综述
[J].发电技术 ,2024 ,45 (6 ):995 -1015 .
[本文引用: 1]
ZHANG J L SONG P LI C QU T M et al Overview of magnetic confinement controlled nuclear fusion reactors and superconducting magnet technologies
[J].Power Generation Technology ,2024 ,45 (6 ):995 -1015 .
[本文引用: 1]
[18]
XU M DUAN X R LIU Y et al Overview of HL-2A recent experiments
[J].Nuclear Fusion , 2019 ,59 (11 ): 112017 .
[本文引用: 1]
[20]
WANG H RAO J HUANG M et al Commissioning results of the 0.5 MW/68 GHz/1.0 s gyrotron on HL-2A electron cyclotron resonance heating system
[J].Fusion Engineering and Design ,2015 ,101 :61 -66 . doi:10.1016/j.fusengdes.2015.09.006
[本文引用: 1]
[21]
SALEWSKI M ASUNTA O ERIKSSON L G et al Comparison of collective Thomson scattering signals due to fast ions in ITER scenarios with fusion and auxiliary heating
[J].Plasma Physics and Controlled Fusion ,2009 ,51 (3 ):035006 . doi:10.1088/0741-3335/51/3/035006
[本文引用: 1]
[22]
STEJNER M NIELSEN S K JACOBSEN A S et al Plasma rotation and ion temperature measurements by collective Thomson scattering at ASDEX Upgrade
[J].Plasma Physics and Controlled Fusion ,2015 ,57 (6 ):062001 . doi:10.1088/0741-3335/57/6/062001
[本文引用: 1]
[23]
MOSEEV D SALEWSKI M Bi-Maxwellian,slowing-down,and ring velocity distributions of fast ions in magnetized plasmas
[J].Physics of Plasmas ,2019 ,26 (2 ):020901 . doi:10.1063/1.5085429
[24]
WEILAND M BILATO R DUX R ,et al RABBIT:real-time simulation of the NBI fast-ion distribution
[J].Nuclear Fusion ,2018 ,58 (8 ):082032 . doi:10.1088/1741-4326/aabf0f
[25]
ABRAMOVIC I SALEWSKI M MOSEEV D Collective Thomson scattering model for arbitrarily driftingbi-Maxwellian velocity distributions
[J].AIP Advances ,2019 ,9 (3 ):035252 . doi:10.1063/1.5088949
[26]
STEJNER M KORSHOLM S B NIELSEN S K et al The prospect for fuel ion ratio measurements in ITER by collective Thomson scattering
[J].Nuclear Fusion ,2012 ,52 (2 ):023011 . doi:10.1088/0029-5515/52/2/023011
[本文引用: 1]
Recent progress in fast-ion diagnostics for magnetically confined plasmas
1
2018
... 快离子是磁约束燃烧等离子体的重要组成部分,是加热等离子体和维持聚变燃烧的重要能量来源.此外,快离子还是托卡马克等离子体中动量和电流的重要来源[1 ] .在未来的磁约束聚变反应堆中,快离子的主要来源是聚变反应产生的能量为3.5 Mev的α 粒子.由于快离子的温度远高于热离子,快离子的动理学特性与热离子有很大差异.因此,对装置内的快离子进行诊断是十分重要且具有挑战性的[2 ] . ...
Recent development of collective Thomson scattering for magnetically confined fusion plasmas
1
2017
... 快离子是磁约束燃烧等离子体的重要组成部分,是加热等离子体和维持聚变燃烧的重要能量来源.此外,快离子还是托卡马克等离子体中动量和电流的重要来源[1 ] .在未来的磁约束聚变反应堆中,快离子的主要来源是聚变反应产生的能量为3.5 Mev的α 粒子.由于快离子的温度远高于热离子,快离子的动理学特性与热离子有很大差异.因此,对装置内的快离子进行诊断是十分重要且具有挑战性的[2 ] . ...
Effects of alpha particles on the scattering function in CO2 laser scattering
1
1986
... 相干汤姆逊散射(collective Thomson scattering,CTS)物理模型的建立以及相应的散射频谱数值计算是设计CTS诊断系统的基础.因此,有必要发展出完备的CTS散射模型代码以支持CTS诊断的开展和诊断系统的设计[3 ] .目前,国内外主流的CTS模型主要是静电模型和全电磁模型.在20世纪80年代,Vahala、Hughes等[4 -5 ] 基于这种静电模型开展了详细的散射频谱理论计算,验证了CTS诊断用于测量α 粒子速度分布函数的可行性.后续的研究发现,当等离子体扰动波矢量与磁场之间接近于垂直时,上述的静电模型不再准确,Aamodt等[6 ] 研究指出,此时需要对等离子体介电函数进行电磁处理.研究中还发现,在一些特定的等离子体参数条件下,静电模型中散射仅来自电子密度扰动的假设是不正确的.为此,研究者[6 -8 ] 进一步发展了全电磁模型.静电模型仅考虑了电子密度的扰动对CTS信号的贡献,而全电磁模型考虑了电场、磁场、电子密度和电流密度扰动对CTS信号的贡献[9 ] .从动理学弗拉索夫方程的角度出发,冷、热等离子体的划分是按其是否受有限温度效应的影响,流体和非流体等离子体的划分是按波的相速度是否远大于粒子的热速度[10 ] .在CTS散射实验中,入射光和散射光的频率足够高,因此等离子体可以被视为这些波的冷源.然而,观察到的扰动的相速度通常与电子的热速度相同或更小,并且可能还必须考虑粒子的非关联运动,因此不可将扰动视为冷集体振荡.这里,冷流体模型不能保证准确,这是因为冷流体模型是由动理学模型基于冷集体振荡假设所推导出来的,它无法体现粒子的非关联运动也无法体现扰动波矢受温度的有限影响,因此Bindslev[7 ] 指出应该回归更加基本的动理学理论. ...
Effect of electrostatic scattering parameters on the direct detection of fusion alphas
1
1988
... 相干汤姆逊散射(collective Thomson scattering,CTS)物理模型的建立以及相应的散射频谱数值计算是设计CTS诊断系统的基础.因此,有必要发展出完备的CTS散射模型代码以支持CTS诊断的开展和诊断系统的设计[3 ] .目前,国内外主流的CTS模型主要是静电模型和全电磁模型.在20世纪80年代,Vahala、Hughes等[4 -5 ] 基于这种静电模型开展了详细的散射频谱理论计算,验证了CTS诊断用于测量α 粒子速度分布函数的可行性.后续的研究发现,当等离子体扰动波矢量与磁场之间接近于垂直时,上述的静电模型不再准确,Aamodt等[6 ] 研究指出,此时需要对等离子体介电函数进行电磁处理.研究中还发现,在一些特定的等离子体参数条件下,静电模型中散射仅来自电子密度扰动的假设是不正确的.为此,研究者[6 -8 ] 进一步发展了全电磁模型.静电模型仅考虑了电子密度的扰动对CTS信号的贡献,而全电磁模型考虑了电场、磁场、电子密度和电流密度扰动对CTS信号的贡献[9 ] .从动理学弗拉索夫方程的角度出发,冷、热等离子体的划分是按其是否受有限温度效应的影响,流体和非流体等离子体的划分是按波的相速度是否远大于粒子的热速度[10 ] .在CTS散射实验中,入射光和散射光的频率足够高,因此等离子体可以被视为这些波的冷源.然而,观察到的扰动的相速度通常与电子的热速度相同或更小,并且可能还必须考虑粒子的非关联运动,因此不可将扰动视为冷集体振荡.这里,冷流体模型不能保证准确,这是因为冷流体模型是由动理学模型基于冷集体振荡假设所推导出来的,它无法体现粒子的非关联运动也无法体现扰动波矢受温度的有限影响,因此Bindslev[7 ] 指出应该回归更加基本的动理学理论. ...
Calculations of Thomson scattering functions for alpha particle diagnostics in JET plasmas
1
1988
... 相干汤姆逊散射(collective Thomson scattering,CTS)物理模型的建立以及相应的散射频谱数值计算是设计CTS诊断系统的基础.因此,有必要发展出完备的CTS散射模型代码以支持CTS诊断的开展和诊断系统的设计[3 ] .目前,国内外主流的CTS模型主要是静电模型和全电磁模型.在20世纪80年代,Vahala、Hughes等[4 -5 ] 基于这种静电模型开展了详细的散射频谱理论计算,验证了CTS诊断用于测量α 粒子速度分布函数的可行性.后续的研究发现,当等离子体扰动波矢量与磁场之间接近于垂直时,上述的静电模型不再准确,Aamodt等[6 ] 研究指出,此时需要对等离子体介电函数进行电磁处理.研究中还发现,在一些特定的等离子体参数条件下,静电模型中散射仅来自电子密度扰动的假设是不正确的.为此,研究者[6 -8 ] 进一步发展了全电磁模型.静电模型仅考虑了电子密度的扰动对CTS信号的贡献,而全电磁模型考虑了电场、磁场、电子密度和电流密度扰动对CTS信号的贡献[9 ] .从动理学弗拉索夫方程的角度出发,冷、热等离子体的划分是按其是否受有限温度效应的影响,流体和非流体等离子体的划分是按波的相速度是否远大于粒子的热速度[10 ] .在CTS散射实验中,入射光和散射光的频率足够高,因此等离子体可以被视为这些波的冷源.然而,观察到的扰动的相速度通常与电子的热速度相同或更小,并且可能还必须考虑粒子的非关联运动,因此不可将扰动视为冷集体振荡.这里,冷流体模型不能保证准确,这是因为冷流体模型是由动理学模型基于冷集体振荡假设所推导出来的,它无法体现粒子的非关联运动也无法体现扰动波矢受温度的有限影响,因此Bindslev[7 ] 指出应该回归更加基本的动理学理论. ...
Alpha particle detection by electromagnetic scattering off of plasma fluctuations
2
1992
... 相干汤姆逊散射(collective Thomson scattering,CTS)物理模型的建立以及相应的散射频谱数值计算是设计CTS诊断系统的基础.因此,有必要发展出完备的CTS散射模型代码以支持CTS诊断的开展和诊断系统的设计[3 ] .目前,国内外主流的CTS模型主要是静电模型和全电磁模型.在20世纪80年代,Vahala、Hughes等[4 -5 ] 基于这种静电模型开展了详细的散射频谱理论计算,验证了CTS诊断用于测量α 粒子速度分布函数的可行性.后续的研究发现,当等离子体扰动波矢量与磁场之间接近于垂直时,上述的静电模型不再准确,Aamodt等[6 ] 研究指出,此时需要对等离子体介电函数进行电磁处理.研究中还发现,在一些特定的等离子体参数条件下,静电模型中散射仅来自电子密度扰动的假设是不正确的.为此,研究者[6 -8 ] 进一步发展了全电磁模型.静电模型仅考虑了电子密度的扰动对CTS信号的贡献,而全电磁模型考虑了电场、磁场、电子密度和电流密度扰动对CTS信号的贡献[9 ] .从动理学弗拉索夫方程的角度出发,冷、热等离子体的划分是按其是否受有限温度效应的影响,流体和非流体等离子体的划分是按波的相速度是否远大于粒子的热速度[10 ] .在CTS散射实验中,入射光和散射光的频率足够高,因此等离子体可以被视为这些波的冷源.然而,观察到的扰动的相速度通常与电子的热速度相同或更小,并且可能还必须考虑粒子的非关联运动,因此不可将扰动视为冷集体振荡.这里,冷流体模型不能保证准确,这是因为冷流体模型是由动理学模型基于冷集体振荡假设所推导出来的,它无法体现粒子的非关联运动也无法体现扰动波矢受温度的有限影响,因此Bindslev[7 ] 指出应该回归更加基本的动理学理论. ...
... [6 -8 ]进一步发展了全电磁模型.静电模型仅考虑了电子密度的扰动对CTS信号的贡献,而全电磁模型考虑了电场、磁场、电子密度和电流密度扰动对CTS信号的贡献[9 ] .从动理学弗拉索夫方程的角度出发,冷、热等离子体的划分是按其是否受有限温度效应的影响,流体和非流体等离子体的划分是按波的相速度是否远大于粒子的热速度[10 ] .在CTS散射实验中,入射光和散射光的频率足够高,因此等离子体可以被视为这些波的冷源.然而,观察到的扰动的相速度通常与电子的热速度相同或更小,并且可能还必须考虑粒子的非关联运动,因此不可将扰动视为冷集体振荡.这里,冷流体模型不能保证准确,这是因为冷流体模型是由动理学模型基于冷集体振荡假设所推导出来的,它无法体现粒子的非关联运动也无法体现扰动波矢受温度的有限影响,因此Bindslev[7 ] 指出应该回归更加基本的动理学理论. ...
A quantitative study of scattering from electromagnetic fluctuations in plasmas
9
1996
... 相干汤姆逊散射(collective Thomson scattering,CTS)物理模型的建立以及相应的散射频谱数值计算是设计CTS诊断系统的基础.因此,有必要发展出完备的CTS散射模型代码以支持CTS诊断的开展和诊断系统的设计[3 ] .目前,国内外主流的CTS模型主要是静电模型和全电磁模型.在20世纪80年代,Vahala、Hughes等[4 -5 ] 基于这种静电模型开展了详细的散射频谱理论计算,验证了CTS诊断用于测量α 粒子速度分布函数的可行性.后续的研究发现,当等离子体扰动波矢量与磁场之间接近于垂直时,上述的静电模型不再准确,Aamodt等[6 ] 研究指出,此时需要对等离子体介电函数进行电磁处理.研究中还发现,在一些特定的等离子体参数条件下,静电模型中散射仅来自电子密度扰动的假设是不正确的.为此,研究者[6 -8 ] 进一步发展了全电磁模型.静电模型仅考虑了电子密度的扰动对CTS信号的贡献,而全电磁模型考虑了电场、磁场、电子密度和电流密度扰动对CTS信号的贡献[9 ] .从动理学弗拉索夫方程的角度出发,冷、热等离子体的划分是按其是否受有限温度效应的影响,流体和非流体等离子体的划分是按波的相速度是否远大于粒子的热速度[10 ] .在CTS散射实验中,入射光和散射光的频率足够高,因此等离子体可以被视为这些波的冷源.然而,观察到的扰动的相速度通常与电子的热速度相同或更小,并且可能还必须考虑粒子的非关联运动,因此不可将扰动视为冷集体振荡.这里,冷流体模型不能保证准确,这是因为冷流体模型是由动理学模型基于冷集体振荡假设所推导出来的,它无法体现粒子的非关联运动也无法体现扰动波矢受温度的有限影响,因此Bindslev[7 ] 指出应该回归更加基本的动理学理论. ...
... 非碰撞的等离子体的微观分布函数f M [7 ] : ...
... 由此,可以推导出接收器接收的散射功率密度谱[7 ] : ...
... 扰动算符量化了等离子体对未屏蔽电流扰动的响应,其表达式[7 ] 如下: ...
... G ^ E , B , j , n }变量的扰动之间的相互作用,以及与散射波的耦合,可被入射波和散射波[7 ] 表示如下: ...
... 从式(19) 和式(31) 可以看出,等离子体介电张量的正确计算是计算散射频谱的关键.在早期的一些理论中,采用冷等离子介电张量,但这种冷等离子体的近似无法正确描述散射过程中由粒子热运动产生的空间色散[7 ] .后续的一些研究表明,热等离子体和相对论等离子体是更完备的近似[8 ] .本文在处理由扰动量产生的散射过程中均采用热等离子体的近似. ...
... 式中:Γ i j a b - 1 7 ]中定义的四阶矩阵的逆矩阵的矩阵元;δ a k δ b l δ a l δ b k χ h i s k j s -1 . ...
... 仍以表1 中ITER装置D-T等离子体的参数为基础,更改ϕ 7 ]表明这种参数下静电结果和全电磁结果会有较大差别.本文的计算结果如图4 所示. ...
... 从图4 中可以看出,密度分量不再完全成为总散射函数的主要成分.在散射波频率小于60.2 GHz时,密度扰动占主要成分;在60.2~60.4 GHz,多种成分一起构成了散射函数;在大于60.4 GHz后,电流密度的扰动占散射函数的主要成分,散射函数的峰值在60.47 GHz处,此处静电模型与全电磁模型的散射函数强度上相差接近1个数量级.由此可见,只有全电磁模型可以正确处理这种特殊的CTS频谱结构.图4 中低频率出现的频谱振荡情况是源于离子-伯恩斯坦波模式,而频谱峰值出现在60.47 GHz处是源于快磁声波[7 ] .CTS频谱中的离子-伯恩斯坦波结构及离子回旋结构是诊断托卡马克装置及聚变堆的离子比例的基础,图5 为全电磁模型CTS散射功率谱随H离子含量变化而产生的不同结构,参数来源于TEXTOR装置CTS系统[15 ] ,如表2 所示,其中R H = n H / n e n H -3 ,离子种类为D-H等离子体,图5 横坐标Z = v s - v i / v c H v i v s v c H
Temporal evolution of confined fast-ion velocity distributions measured by collective Thomson scattering in TEXTOR
2
2008
... 相干汤姆逊散射(collective Thomson scattering,CTS)物理模型的建立以及相应的散射频谱数值计算是设计CTS诊断系统的基础.因此,有必要发展出完备的CTS散射模型代码以支持CTS诊断的开展和诊断系统的设计[3 ] .目前,国内外主流的CTS模型主要是静电模型和全电磁模型.在20世纪80年代,Vahala、Hughes等[4 -5 ] 基于这种静电模型开展了详细的散射频谱理论计算,验证了CTS诊断用于测量α 粒子速度分布函数的可行性.后续的研究发现,当等离子体扰动波矢量与磁场之间接近于垂直时,上述的静电模型不再准确,Aamodt等[6 ] 研究指出,此时需要对等离子体介电函数进行电磁处理.研究中还发现,在一些特定的等离子体参数条件下,静电模型中散射仅来自电子密度扰动的假设是不正确的.为此,研究者[6 -8 ] 进一步发展了全电磁模型.静电模型仅考虑了电子密度的扰动对CTS信号的贡献,而全电磁模型考虑了电场、磁场、电子密度和电流密度扰动对CTS信号的贡献[9 ] .从动理学弗拉索夫方程的角度出发,冷、热等离子体的划分是按其是否受有限温度效应的影响,流体和非流体等离子体的划分是按波的相速度是否远大于粒子的热速度[10 ] .在CTS散射实验中,入射光和散射光的频率足够高,因此等离子体可以被视为这些波的冷源.然而,观察到的扰动的相速度通常与电子的热速度相同或更小,并且可能还必须考虑粒子的非关联运动,因此不可将扰动视为冷集体振荡.这里,冷流体模型不能保证准确,这是因为冷流体模型是由动理学模型基于冷集体振荡假设所推导出来的,它无法体现粒子的非关联运动也无法体现扰动波矢受温度的有限影响,因此Bindslev[7 ] 指出应该回归更加基本的动理学理论. ...
... 从式(19) 和式(31) 可以看出,等离子体介电张量的正确计算是计算散射频谱的关键.在早期的一些理论中,采用冷等离子介电张量,但这种冷等离子体的近似无法正确描述散射过程中由粒子热运动产生的空间色散[7 ] .后续的一些研究表明,热等离子体和相对论等离子体是更完备的近似[8 ] .本文在处理由扰动量产生的散射过程中均采用热等离子体的近似. ...
Electron density fluctuations in a plasma
2
1960
... 相干汤姆逊散射(collective Thomson scattering,CTS)物理模型的建立以及相应的散射频谱数值计算是设计CTS诊断系统的基础.因此,有必要发展出完备的CTS散射模型代码以支持CTS诊断的开展和诊断系统的设计[3 ] .目前,国内外主流的CTS模型主要是静电模型和全电磁模型.在20世纪80年代,Vahala、Hughes等[4 -5 ] 基于这种静电模型开展了详细的散射频谱理论计算,验证了CTS诊断用于测量α 粒子速度分布函数的可行性.后续的研究发现,当等离子体扰动波矢量与磁场之间接近于垂直时,上述的静电模型不再准确,Aamodt等[6 ] 研究指出,此时需要对等离子体介电函数进行电磁处理.研究中还发现,在一些特定的等离子体参数条件下,静电模型中散射仅来自电子密度扰动的假设是不正确的.为此,研究者[6 -8 ] 进一步发展了全电磁模型.静电模型仅考虑了电子密度的扰动对CTS信号的贡献,而全电磁模型考虑了电场、磁场、电子密度和电流密度扰动对CTS信号的贡献[9 ] .从动理学弗拉索夫方程的角度出发,冷、热等离子体的划分是按其是否受有限温度效应的影响,流体和非流体等离子体的划分是按波的相速度是否远大于粒子的热速度[10 ] .在CTS散射实验中,入射光和散射光的频率足够高,因此等离子体可以被视为这些波的冷源.然而,观察到的扰动的相速度通常与电子的热速度相同或更小,并且可能还必须考虑粒子的非关联运动,因此不可将扰动视为冷集体振荡.这里,冷流体模型不能保证准确,这是因为冷流体模型是由动理学模型基于冷集体振荡假设所推导出来的,它无法体现粒子的非关联运动也无法体现扰动波矢受温度的有限影响,因此Bindslev[7 ] 指出应该回归更加基本的动理学理论. ...
... CTS的原理是将入射的电磁波束(通常在毫米波范围内)散射到电子分布中的微观集体涨落上并发出散射辐射,这些涨落是由运动离子的德拜屏蔽引起的.通过设置接收天线的角度,可以对某个特定空间位置发出的散射辐射进行接收,这就确定了散射的几何结构.要实现这种电子的微观集体涨落,需要入射波和散射几何结构满足Salpeter准则[9 ] : ...
Three-wave mixing and Thomson scattering in plasmas
3
1993
... 相干汤姆逊散射(collective Thomson scattering,CTS)物理模型的建立以及相应的散射频谱数值计算是设计CTS诊断系统的基础.因此,有必要发展出完备的CTS散射模型代码以支持CTS诊断的开展和诊断系统的设计[3 ] .目前,国内外主流的CTS模型主要是静电模型和全电磁模型.在20世纪80年代,Vahala、Hughes等[4 -5 ] 基于这种静电模型开展了详细的散射频谱理论计算,验证了CTS诊断用于测量α 粒子速度分布函数的可行性.后续的研究发现,当等离子体扰动波矢量与磁场之间接近于垂直时,上述的静电模型不再准确,Aamodt等[6 ] 研究指出,此时需要对等离子体介电函数进行电磁处理.研究中还发现,在一些特定的等离子体参数条件下,静电模型中散射仅来自电子密度扰动的假设是不正确的.为此,研究者[6 -8 ] 进一步发展了全电磁模型.静电模型仅考虑了电子密度的扰动对CTS信号的贡献,而全电磁模型考虑了电场、磁场、电子密度和电流密度扰动对CTS信号的贡献[9 ] .从动理学弗拉索夫方程的角度出发,冷、热等离子体的划分是按其是否受有限温度效应的影响,流体和非流体等离子体的划分是按波的相速度是否远大于粒子的热速度[10 ] .在CTS散射实验中,入射光和散射光的频率足够高,因此等离子体可以被视为这些波的冷源.然而,观察到的扰动的相速度通常与电子的热速度相同或更小,并且可能还必须考虑粒子的非关联运动,因此不可将扰动视为冷集体振荡.这里,冷流体模型不能保证准确,这是因为冷流体模型是由动理学模型基于冷集体振荡假设所推导出来的,它无法体现粒子的非关联运动也无法体现扰动波矢受温度的有限影响,因此Bindslev[7 ] 指出应该回归更加基本的动理学理论. ...
... 在相干汤姆逊散射过程中,扰动电场和扰动电流满足方程[10 ] : ...
... 在入射波和散射波的色散关系以及耦合算符的计算中也需要考虑等离子体的介电性质.由于入射波和散射波是高频的电磁波且耦合算符仅与入射波和散射波有关,这时冷等离子体的近似是恰当的.在确定了等离子体介电性质后,散射波的三阶伪张量的矩阵元[10 ] 便可被表示为 ...
Design and development of the ITER CTS diagnostic
1
2019
... 为保证本文全电磁模型散射频谱计算代码的准确性与可靠性,分别利用静电模型和全电磁模型计算散射函数进行对比验证.输入参数选取了国际热核聚变实验反应堆(international thermonuclear experimental reactor,ITER)装置设计的CTS诊断系统及等离子体参数[11 -13 ] ,如表1 所示.其中,快离子为α 粒子,且服从初始温度为3.5 MeV的经典慢化分布. ...
Inference of α -particle density profiles from ITER collective Thomson scattering
0
2019
ITER collective Thomson scattering:preparing to diagnose fusion-born alpha particles (invited)
1
2022
... 为保证本文全电磁模型散射频谱计算代码的准确性与可靠性,分别利用静电模型和全电磁模型计算散射函数进行对比验证.输入参数选取了国际热核聚变实验反应堆(international thermonuclear experimental reactor,ITER)装置设计的CTS诊断系统及等离子体参数[11 -13 ] ,如表1 所示.其中,快离子为α 粒子,且服从初始温度为3.5 MeV的经典慢化分布. ...
Measurements of intrinsic ion Bernstein waves in a tokamak by collective Thomson scattering
2
2011
... 虽然在大多数情况下,密度扰动产生的散射功率远大于其他扰动量产生的散射功率,但当扰动波矢与磁场间的夹角ϕ [14 ] 结构和离子回旋结构会在趋近于90°时出现,这是因为在ϕ k ∥ [15 ] .这种结构对于CTS系统诊断聚变堆燃料比是必不可少的.因此,有必要对趋近于90°时的CTS全电磁模型频谱结构进行研究和分析. ...
... 从图5 中可以看出,CTS频谱中的离子-伯恩斯坦波结构及离子回旋结构对H离子浓度的敏感性相对较高,类似的结果在2011年TEXTOR装置利用CTS观测离子伯恩斯坦波的实验与模拟中也被验证[14 -15 ] .这说明本文采用的全电磁模型代码可以作为聚变装置诊断离子比例的基础. ...
Principles of fuel ion ratio measurements in fusion plasmas by collective Thomson scattering
3
2011
... 虽然在大多数情况下,密度扰动产生的散射功率远大于其他扰动量产生的散射功率,但当扰动波矢与磁场间的夹角ϕ [14 ] 结构和离子回旋结构会在趋近于90°时出现,这是因为在ϕ k ∥ [15 ] .这种结构对于CTS系统诊断聚变堆燃料比是必不可少的.因此,有必要对趋近于90°时的CTS全电磁模型频谱结构进行研究和分析. ...
... 从图4 中可以看出,密度分量不再完全成为总散射函数的主要成分.在散射波频率小于60.2 GHz时,密度扰动占主要成分;在60.2~60.4 GHz,多种成分一起构成了散射函数;在大于60.4 GHz后,电流密度的扰动占散射函数的主要成分,散射函数的峰值在60.47 GHz处,此处静电模型与全电磁模型的散射函数强度上相差接近1个数量级.由此可见,只有全电磁模型可以正确处理这种特殊的CTS频谱结构.图4 中低频率出现的频谱振荡情况是源于离子-伯恩斯坦波模式,而频谱峰值出现在60.47 GHz处是源于快磁声波[7 ] .CTS频谱中的离子-伯恩斯坦波结构及离子回旋结构是诊断托卡马克装置及聚变堆的离子比例的基础,图5 为全电磁模型CTS散射功率谱随H离子含量变化而产生的不同结构,参数来源于TEXTOR装置CTS系统[15 ] ,如表2 所示,其中R H = n H / n e n H -3 ,离子种类为D-H等离子体,图5 横坐标Z = v s - v i / v c H v i v s v c H
... 从图5 中可以看出,CTS频谱中的离子-伯恩斯坦波结构及离子回旋结构对H离子浓度的敏感性相对较高,类似的结果在2011年TEXTOR装置利用CTS观测离子伯恩斯坦波的实验与模拟中也被验证[14 -15 ] .这说明本文采用的全电磁模型代码可以作为聚变装置诊断离子比例的基础. ...
磁约束可控核聚变装置的磁体系统综述
1
2024
... 目前国内的托卡马克上尚未系统性地开展CTS诊断研究,一定程度上不利于相关技术[16 ] 的发展.HL-2A装置上建有完备的中性束注入(neutral beam injection heating,NBI)系统和电子回旋加热(electron cyclotron resonance heating,ECRH)系统,能为国内CTS诊断研究的开展提供较好的平台支撑.因此,亟须研究HL-2A装置上的散射频谱特性. ...
Overview of magnetic confinement controlled nuclear fusion reactors and superconducting magnet technologies
1
2024
... 目前国内的托卡马克上尚未系统性地开展CTS诊断研究,一定程度上不利于相关技术[16 ] 的发展.HL-2A装置上建有完备的中性束注入(neutral beam injection heating,NBI)系统和电子回旋加热(electron cyclotron resonance heating,ECRH)系统,能为国内CTS诊断研究的开展提供较好的平台支撑.因此,亟须研究HL-2A装置上的散射频谱特性. ...
HL-2A 装置中高能量粒子驱动的非线性不稳定行为研究
1
2019
... HL-2A装置是由核工业西南物理研究院建造的磁约束核聚变装置[17 -18 ] ,同时也是我国第一个具有偏滤器位形的大型托卡马克装置.HL-2A装置上建有5 MW ECRH系统.该系统主要包含6支0.5 MW/68 GHz/1 s回旋管和2支1 MW/140 GHz/3 s回旋管,其还可以运行在0.5 MW/105 GHz/0.1 s的输出模式下[19 -20 ] .因此,如果基于HL-2A装置的ECRH系统搭建CTS诊断系统,探测波频率可以选择的有68 GHz、105 GHz 和140 GHz.当频率选择为68 GHz时,且纵场为 1.84~2.43 T时,2次谐波共振层位于高场侧,入射的微波在经过测量位置后可能会被等离子体吸收,此时接收波束也可能穿过2次谐波共振层,导致较强的电子回旋辐射被散射信号接收系统收集,这会进一步减小信噪比.故在纵场为2 T附近时,不宜选用68 GHz作为探测波频率.本文研究的HL-2A装置的CTS诊断系统将基于105 GHz和140 GHz两种频率进行设计. ...
Study of nonlinear instabilities driven by energetic particles in HL-2A Tokamak
1
2019
... HL-2A装置是由核工业西南物理研究院建造的磁约束核聚变装置[17 -18 ] ,同时也是我国第一个具有偏滤器位形的大型托卡马克装置.HL-2A装置上建有5 MW ECRH系统.该系统主要包含6支0.5 MW/68 GHz/1 s回旋管和2支1 MW/140 GHz/3 s回旋管,其还可以运行在0.5 MW/105 GHz/0.1 s的输出模式下[19 -20 ] .因此,如果基于HL-2A装置的ECRH系统搭建CTS诊断系统,探测波频率可以选择的有68 GHz、105 GHz 和140 GHz.当频率选择为68 GHz时,且纵场为 1.84~2.43 T时,2次谐波共振层位于高场侧,入射的微波在经过测量位置后可能会被等离子体吸收,此时接收波束也可能穿过2次谐波共振层,导致较强的电子回旋辐射被散射信号接收系统收集,这会进一步减小信噪比.故在纵场为2 T附近时,不宜选用68 GHz作为探测波频率.本文研究的HL-2A装置的CTS诊断系统将基于105 GHz和140 GHz两种频率进行设计. ...
Overview of HL-2A recent experiments
1
2019
... HL-2A装置是由核工业西南物理研究院建造的磁约束核聚变装置[17 -18 ] ,同时也是我国第一个具有偏滤器位形的大型托卡马克装置.HL-2A装置上建有5 MW ECRH系统.该系统主要包含6支0.5 MW/68 GHz/1 s回旋管和2支1 MW/140 GHz/3 s回旋管,其还可以运行在0.5 MW/105 GHz/0.1 s的输出模式下[19 -20 ] .因此,如果基于HL-2A装置的ECRH系统搭建CTS诊断系统,探测波频率可以选择的有68 GHz、105 GHz 和140 GHz.当频率选择为68 GHz时,且纵场为 1.84~2.43 T时,2次谐波共振层位于高场侧,入射的微波在经过测量位置后可能会被等离子体吸收,此时接收波束也可能穿过2次谐波共振层,导致较强的电子回旋辐射被散射信号接收系统收集,这会进一步减小信噪比.故在纵场为2 T附近时,不宜选用68 GHz作为探测波频率.本文研究的HL-2A装置的CTS诊断系统将基于105 GHz和140 GHz两种频率进行设计. ...
Recent progress of 2 MW 140 GHz ECRH system on HL-2A
1
2012
... HL-2A装置是由核工业西南物理研究院建造的磁约束核聚变装置[17 -18 ] ,同时也是我国第一个具有偏滤器位形的大型托卡马克装置.HL-2A装置上建有5 MW ECRH系统.该系统主要包含6支0.5 MW/68 GHz/1 s回旋管和2支1 MW/140 GHz/3 s回旋管,其还可以运行在0.5 MW/105 GHz/0.1 s的输出模式下[19 -20 ] .因此,如果基于HL-2A装置的ECRH系统搭建CTS诊断系统,探测波频率可以选择的有68 GHz、105 GHz 和140 GHz.当频率选择为68 GHz时,且纵场为 1.84~2.43 T时,2次谐波共振层位于高场侧,入射的微波在经过测量位置后可能会被等离子体吸收,此时接收波束也可能穿过2次谐波共振层,导致较强的电子回旋辐射被散射信号接收系统收集,这会进一步减小信噪比.故在纵场为2 T附近时,不宜选用68 GHz作为探测波频率.本文研究的HL-2A装置的CTS诊断系统将基于105 GHz和140 GHz两种频率进行设计. ...
Commissioning results of the 0.5 MW/68 GHz/1.0 s gyrotron on HL-2A electron cyclotron resonance heating system
1
2015
... HL-2A装置是由核工业西南物理研究院建造的磁约束核聚变装置[17 -18 ] ,同时也是我国第一个具有偏滤器位形的大型托卡马克装置.HL-2A装置上建有5 MW ECRH系统.该系统主要包含6支0.5 MW/68 GHz/1 s回旋管和2支1 MW/140 GHz/3 s回旋管,其还可以运行在0.5 MW/105 GHz/0.1 s的输出模式下[19 -20 ] .因此,如果基于HL-2A装置的ECRH系统搭建CTS诊断系统,探测波频率可以选择的有68 GHz、105 GHz 和140 GHz.当频率选择为68 GHz时,且纵场为 1.84~2.43 T时,2次谐波共振层位于高场侧,入射的微波在经过测量位置后可能会被等离子体吸收,此时接收波束也可能穿过2次谐波共振层,导致较强的电子回旋辐射被散射信号接收系统收集,这会进一步减小信噪比.故在纵场为2 T附近时,不宜选用68 GHz作为探测波频率.本文研究的HL-2A装置的CTS诊断系统将基于105 GHz和140 GHz两种频率进行设计. ...
Comparison of collective Thomson scattering signals due to fast ions in ITER scenarios with fusion and auxiliary heating
1
2009
... 本文分别研究HL-2A装置上2种散射几何和105、140 GHz探测波频率的CTS散射能量谱,以优化CTS诊断系统参数.这2种散射几何分别为Ⅰ(θ ϕ θ ϕ [21 ] .散射能量谱的计算输入参数如表3 所示,主离子和快离子均为氘离子.2种探测波频率下2种散射几何的计算结果分别如图6 和图7 所示.可以看出,105 GHz的快离子诊断区域相对较宽,且散射能量更大,这意味着更好的信噪比,故探测波频率应选择105 GHz.在105 GHz的探测波频率下,2种散射几何的快离子诊断区域相差不大,但散射几何Ⅱ的散射能量更大.同时,散射几何Ⅰ对快离子平行于磁场方向上速度具有高分辨率,这有利于后续利用CTS系统诊断快离子分布的各向异性. ...
Plasma rotation and ion temperature measurements by collective Thomson scattering at ASDEX Upgrade
1
2015
... 综合考虑,选择105 GHz CTS诊断系统在散射几何Ⅱ下对表3 给定参数进行常规快离子诊断,在散射几何Ⅰ下进行快离子各向异性的诊断[22 -26 ] .HL-2A装置的CTS诊断系统同样具有诊断离子含量的能力.更改ϕ 图8 所示.这说明CTS诊断系统具有在HL-2A上诊断离子比例的潜力.此外,温度对频谱的影响也不可忽视.由图6 可见,在105 GHz散射几何Ⅱ的情况下,电子频谱是影响快离子诊断区间的关键,故提升电子温度会提升电子频谱能量及降低快离子诊断区间宽度.如图9 所示,提升电子温度分别为2.5 keV和3.5 keV,电子的频谱能量逐渐变强并导致快离子诊断区间变窄. ...
Bi-Maxwellian,slowing-down,and ring velocity distributions of fast ions in magnetized plasmas
0
2019
RABBIT:real-time simulation of the NBI fast-ion distribution
0
2018
Collective Thomson scattering model for arbitrarily driftingbi-Maxwellian velocity distributions
0
2019
The prospect for fuel ion ratio measurements in ITER by collective Thomson scattering
1
2012
... 综合考虑,选择105 GHz CTS诊断系统在散射几何Ⅱ下对表3 给定参数进行常规快离子诊断,在散射几何Ⅰ下进行快离子各向异性的诊断[22 -26 ] .HL-2A装置的CTS诊断系统同样具有诊断离子含量的能力.更改ϕ 图8 所示.这说明CTS诊断系统具有在HL-2A上诊断离子比例的潜力.此外,温度对频谱的影响也不可忽视.由图6 可见,在105 GHz散射几何Ⅱ的情况下,电子频谱是影响快离子诊断区间的关键,故提升电子温度会提升电子频谱能量及降低快离子诊断区间宽度.如图9 所示,提升电子温度分别为2.5 keV和3.5 keV,电子的频谱能量逐渐变强并导致快离子诊断区间变窄. ...