0 引言
随着风电大量接入电网,其诱发的次同步振荡(subsynchronous oscillation,SSO)现象对电力系统安全稳定运行构成了严重的威胁[1 -5 ] 。2015年新疆哈密地区大规模直驱风电机组出现次同步振荡[6 ] ,给电网稳定运行造成重要影响。
为此,学者们对直驱风机并网诱发SSO问题进行了广泛的研究。文献[7 -8 ]针对风电机组的次同步振荡问题,从特性、分析方法和抑制措施等方面进行了综述。文献[9 -11 ]研究指出,直驱风电机组并入弱电网诱发SSO现象的主要因素之一是网侧变流器与电网之间的交互作用。文献[12 ]研究表明,直驱风机控制系统锁相环参数、电流内环参数对SSO有明显的影响。文献[13 ]用自抗扰控制(active disturbance rejection control,ADRC)替换电流内环PI控制器,并阐述ADRC抑制SSO原理,但其控制器参数整定过于繁琐。文献[14 ]建立直驱式风机并网变流器数学模型,用线性自抗扰控制(linear active disturbance rejection control,ADRC)替换电流内环PI控制器,简化了控制器参数整定的难度。文献[15 ]提出一阶LADRC电流内环控制器设计,可抵消线路中的次同步频率分量,虽能有效抑制SSO现象,但存在较大的误差与超调量。文献[16 ]提出基于一阶总扰动偏差控制的微分前馈LADRC,该控制器不仅可以减小跟踪误差且具有较强的抗干扰性能,但其不足之处在于功率波动范围较大。文献[17 ]在dq 坐标系下建立了网侧变流器的阻抗模型,并结合广义Nyquist判据对风电并网系统稳定性影响因素进行了分析。文献[18 ]分析了接入电网强度对并网系统稳定性的影响。
本文在传统LADRC的基础上,提出改进线性状态误差反馈(linear state error feedback,LSEF)控制律,从而得到一种能较好的抑制SSO的改进LADRC电流内环控制器,可以更好地缩小功率波动范围,减小跟踪误差,抑制SSO现象。
1 直驱风机并网数学建模
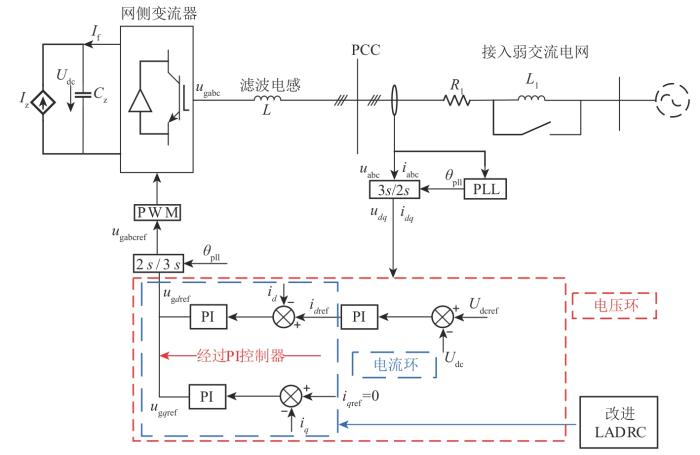
将直驱风机等效为恒功率电流源,则直驱风机并入弱电网及其网侧变流器控制结构如图1 所示,图中:u a b c 、 u d , q dq 轴分量;U d c 、 U d c r e f u g a b c u g d , q r e f dq 轴参考值;u g a b c r e f i a b c i d , q dq 轴分量;i d r e f i q r e f dq 轴电流参考值;θ p l l C z 、 L 、 L 1 、 R 1 I f 、 I z
图1
图1
网侧变流器控制结构图
Fig. 1
Control structure of grid side converter
u g d = u d - L d i d d t - R 1 i d + ω L i q u g q = u q - L d i q d t - R 1 i q - ω L i d (1)
式中:u g d u g q d 轴与q 轴分量;u d u q d 轴与q 轴
2 改进LADRC控制策略设计
本文将结合传统LADRC和一次微分前馈项环节,继续改进LSEF来补偿扰动项,减小跟踪误差及扰动项对并网系统稳定性的影响。由于线性微分跟踪器会在系统进入稳态后引起高频颤振[19 ] ,因此本文只考虑LADRC由线性扩张状态观察器(linear extended state observer,LESO)与LSEF构成的LADRC。
y ˙ = d x 1 d t = b 0 u + f (2)
式中:x 1 dq 轴电流;b 0 = - 1 L u dq 轴电压;y ˙ f
z ˙ 1 = z 2 + b 0 u - β 1 ( z 1 - y ) z ˙ 2 = - β 2 ( z 1 - y ) (3)
式中:z 1 、 z 2 x 1 、 x 2 x 2 u 、 y β 1 β 2
根据极点配置法,将式(3)的极点配置在LESO的带宽ω 0 β 1 = 2 ω 0 β 2 = ω 0 2
二阶LESO的跟踪状态变量的输出误差e 1 e 2
e 1 = z 1 - y e 2 = z 2 - f (4)
e ˙ 1 = - β 1 e 1 + e 2 e ˙ 2 = - β 2 e 1 - f ˙ (5)
由于LSEF是对输入信号及其微分,以及LESO观测到的系统输出及其微分的误差进行控制和扰动补偿,因此,本文提出改进LSEF对扰动项进行补偿,以减小跟踪误差以及扰动项对并网系统稳定性的影响。
LESO可替代传统PID控制中积分器的作用,因而LSEF可以简化为PD组合设计。针对一阶系统,本文采用二阶LESO,LSEF采用P控制器。
y ˙ = f + b 0 u = f + k p ( v - z 1 ) - z 2 =
- k p e 1 - e 2 - k p y + k p v =
E - k p y + k p v ) (6)
式中:k p = ω c v E = - k p e 1 - e 2 E
e 2 ( s ) = ( s + β 1 ) e 1 ( s ) (7)
将式(7)进行拉氏反变换,代入理想误差项E = - k p e 1 - e 2
E = - ( k p + β 1 ) e 1 - e ˙ 1 (8)
式(8)中的e 1 e ˙ 1
E ¯ = - ( k p + β 1 ) e 1 (9)
通过以上分析,结合文献[16 ]对输入信号进行一阶求导,从而提高系统响应速度、减小跟踪误差、缩小功率波动范围。故改进LADRC的数学模型为:
z ˙ 1 = z 2 + b 0 u - β 1 ( z 1 - y ) z ˙ 2 = - β 2 ( z 1 - y ) u 0 = k p ( v - z 1 ) u = v ˙ + u 0 - z 2 - E ¯ b 0 (10)
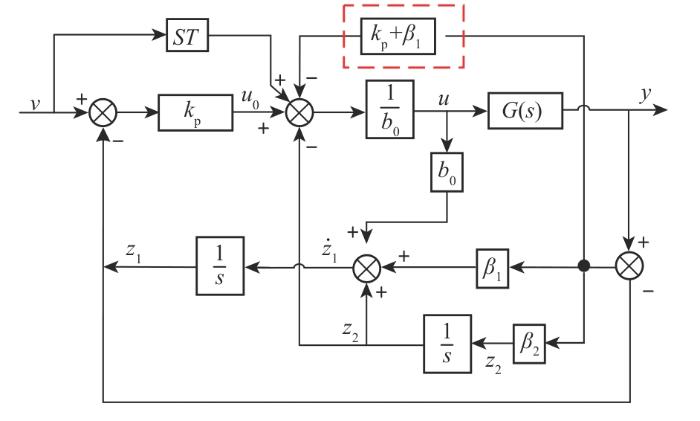
根据式(10)可得改进LADRC的结构控制框图如图2 所示,其中,ST 表示对信号进行微分;G (s )为闭环传递函数。
图2
图2
改进LADRC控制框图
Fig. 2
Improved LADRC control block diagram
3 改进LADRC性能分析
3.1 改进LADRC跟踪误差分析
e ( t ) = v ( t ) - y ( t ) (11)
对式(11)进行微分,并将式(10)中的u 0 、 u
e ˙ ( t ) = v ˙ ( t ) - y ˙ ( t ) = v ˙ ( t ) - b 0 u - f = v ˙ ( t ) - f - v ˙ ( t ) - u 0 + z 2 + E ¯ = z 2 - f - k p e - β 1 ( z 1 - y ) (12)
e ( s ) = Z 2 ( s ) - F ( s ) - β 1 ( z 1 - y ) s + k p (13)
e ( s ) = s V ( s ) + Z 2 ( s ) - F ( s ) s + k p (14)
式中V ( s ) Z 2 ( s ) F ( s ) v z 2 f 的拉氏变换。
比较式(13)、(14)可知,改进LADRC不仅能消除输入信号相关的误差量s V ( s ) / ( s + k p ) ,且使得总扰动的估计误差也减小了β 1 ( z 1 - y ) / ( s + k p )
3.2 改进LADRC抗扰性能分析
y ˙ = f + b 0 v ˙ + k p ( v - z 1 ) - z 2 - E ¯ b 0 (15)
从而得到带有LESO估计误差补偿的LSEF控制器输出,表示为
u = 1 b 0 [ v ˙ + ω c ( v - z 1 ) - z 2 + ( k p + β 1 ) e 1 ] (16)
U ( s ) = 1 b 0 ( s + ω 0 ) 2 s 2 { ( s + ω c ) V ( s ) - [ ω c + ω 0 s ( 2 s + ω 0 ) ( s + ω 0 ) 2 ] Y ( s ) } (17)
令H ( s ) = ω c ( s + ω 0 ) 2 + ω 0 s ( 2 s + ω 0 ) ( s + ω 0 ) 2 G 1 ( s ) = ( s + ω 0 ) 2 s 2 式(2)进行拉氏变换后代入式(17)并化简可得y 的拉氏变换:
Y ( s ) = s 2 ( s + ω c ) ( s + ω 0 ) 2 F ( s ) + V ( s ) (18)
同理,可得传统LADRC输出项与输入项、扰动项之间的关系为
Y ( s ) = s ( s + 2 ω 0 + ω c ) ( ω c + s ) ( s + ω 0 ) 2 F ( s ) + ω c ω c + s V ( s ) (19)
比较式(18)、(19)可知,改进LADRC的输入信号比传统LADRC少了一阶微分前馈环节ω c / ( s + ω c ) 2 ω 0 s + ω c s
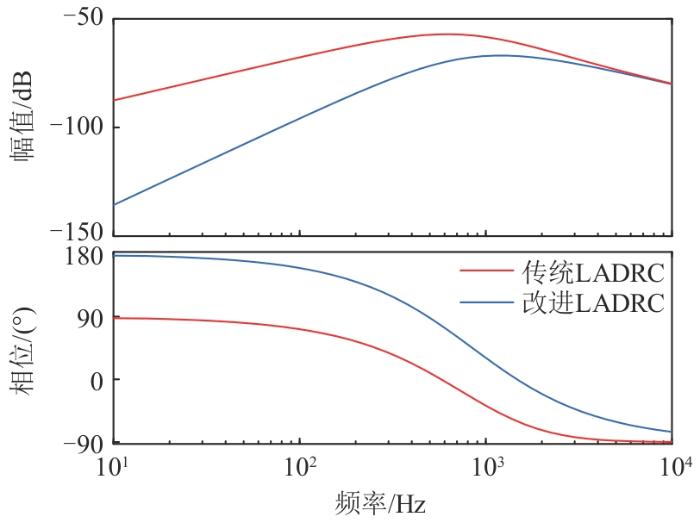
仅考虑扰动项时,取相同的ω 0 、 ω c [22 ] 如图3 所示。
图3
图3
系统扰动项伯德图
Fig. 3
Bode diagram of system disturbance term
由图3 可知,改进LADRC在中低频段扰动增益明显小于传统LADRC,且其相位也明显滞后,所以在扰动输入时改进LADRC具有更好的抗扰作用。
3.3 控制策略暂态性能验证
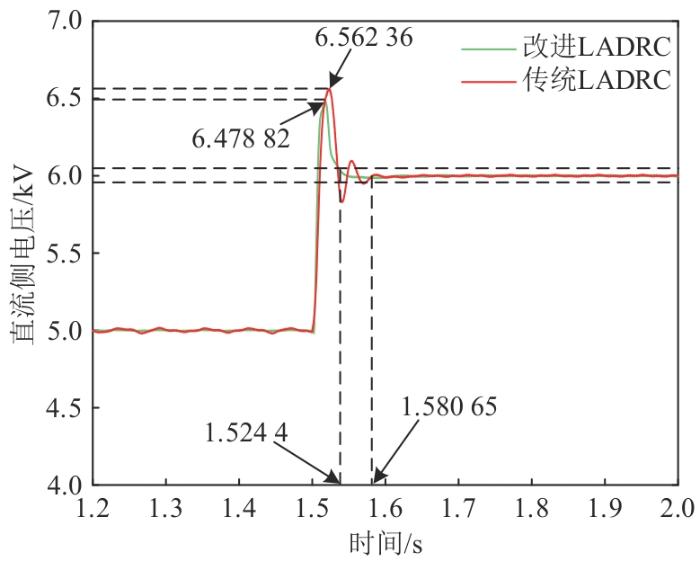
为了验证所改进控制策略的暂态性能,设置极弱电网短路比(short circuit ratio,SCR)为1.9,低风速工况,直流侧电压在t =1.5 s时阶跃至6 kV。传统LADRC与改进LADRC暂态性能对比如图4 所示,暂态特性对比如表1 所示。
图4
图4
传统LADRC与改进LADRC暂态性能对比图
Fig. 4
Comparison of transient performance between traditional LADRC and improved LADRC
从图4 、表1 可以看出,在极弱电网工况下,相较于传统LADRC,改进LADRC调节时间减少了0.06 s,超调量减少了1.31%,表明改进LADRC有更好的暂态性能且抗干扰能力更强。
4 线路阻抗对并网系统稳定性的影响
风电基本与负荷中心呈逆向分布,因此风电的大规模利用与消纳需要进行长距离输送[21 ] ,而风电场与大型电网之间的线路阻抗已成为影响SSO的主要因素,故研究线路阻抗值对并网系统稳定性尤为重要。
4.1 改进LADRC的阻抗模型
建立包括线路阻抗和各个控制环节,且能够反映SSO现象的等效阻抗模型,进而分析线路阻抗对系统稳定性产生的影响。
以d 轴为例,LSEF的输出信号为u d 轴的调制信号m d y I d 图2 可得:
m d = 1 b 0 [ I ˙ d r + k p ( I d r - I d ) - z 2 + β 1 e 1 ] (20)
式中I d r I d
对式(10)进行拉氏变换,将式(20)代入可得频域下的Z 1 、 Z 2
Z 1 = 2 ω 0 s + ω 0 2 ( s + ω 0 ) 2 I d + b 0 s ( s + ω 0 ) 2 m d Z 2 = ω 0 2 s ( s + ω 0 ) 2 I d - b 0 ω 0 2 ( s + ω 0 ) 2 m d (21)
联立式(20)、(21),得出d 轴调制信号在频域中扰动分量的表达式如下:
m d = [ ( I d r - I d ) P 1 ( s ) - P 2 ( s ) I 1 ] (22)
P 1 ( s ) = ( s + ω 0 ) 2 ( 1 + k p s ) b 0 s 3 (23)
P 2 ( s ) = ( s + ω 0 ) 2 - ω 0 s 2 ( 2 s + ω 0 ) b 0 s 3 (24)
根据文献[22 -23 ]得到弱电网情况下线路阻抗和各个控制环节,且能够反应SSO现象的等效阻抗模型为
Y = ( I v i - Z i v + L m ) - 1 ( E - Z v v - P θ v ) (25)
式中:L m = d i a g ( s L f , s 1 L f ) E P θ v I v i Z v v 、 Z i v
Z i v = 3 K m [ M 1 + Q P 1 ( s 1 ) ] S * 4 ( I s - s 1 C z U d c 0 ) [ M 1 * + Q P 1 ( s 1 ) ] S 4 ( I s - s 1 C z U d c 0 ) [ M 1 * + Q P 1 ( s 1 ) ] S * 4 ( I s - s 1 C z U d c 0 ) [ M 1 * + Q P 1 ( s 1 ) ] S 4 ( I s - s 1 C z U d c 0 ) (26)
P θ v = 1 2 T p l l ( s 1 ) P i ( s 1 ) I 1 + M 1 - P i ( s 1 ) I 1 - M 1 - P i ( s 1 ) I 1 * - M 1 * P i ( s 1 ) I 1 * + M 1 * (27)
Z v v = 3 K m [ M 1 + Q P 1 ( s 1 ) ] I 1 * 4 ( I s - s 1 C z U d c 0 ) [ M 1 * + Q P 1 ( s 1 ) ] I 1 4 ( I s - s 1 C z U d c 0 ) [ M 1 * + Q P 1 ( s 1 ) ] I 1 * 4 ( I s - s 1 C z U d c 0 ) [ M 1 * + Q P 1 ( s 1 ) ] I 1 4 ( I s - s 1 C z U d c 0 ) (28)
式中:T p l l ( s 1 ) = H p l l ( s 1 ) / [ 1 + U 1 H p l l ( s 1 ) ] H p l l M 1 、 M 1 * I 1 、 I 1 * K m S * = U 1 + s 1 L f I 1 * Q = U d c 0 H v ( s 1 ) P i ( s 1 ) = P 1 ( s 1 ) + P 2 ( s 1 )
4.2 阻抗模型仿真验证
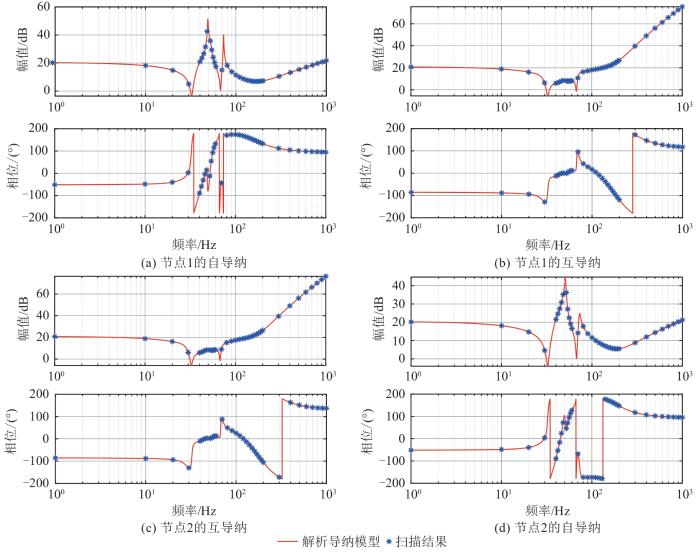
为验证上述阻抗模型的正确性,根据考虑频率耦合效应时的正序导纳的数学模型[24 ] 和表1 参数,在仿真软件进行扫频,得到导纳模型线路。阻抗分别取3、2.3、1.95 mH(对应SCR分别为1.9、2.5、2.9)。
仿真结果如图5 所示。结果表明,解析导纳曲线和仿真得到的导纳点能够较好地吻合,从而验证了本文建立的阻抗模型的正确性。
图5
图5
改进LADRC网侧变流器导纳模型验证
Fig. 5
Verification of the admittance model of the improved LADRC network side converter
4.3 线路阻抗对并网系统的影响
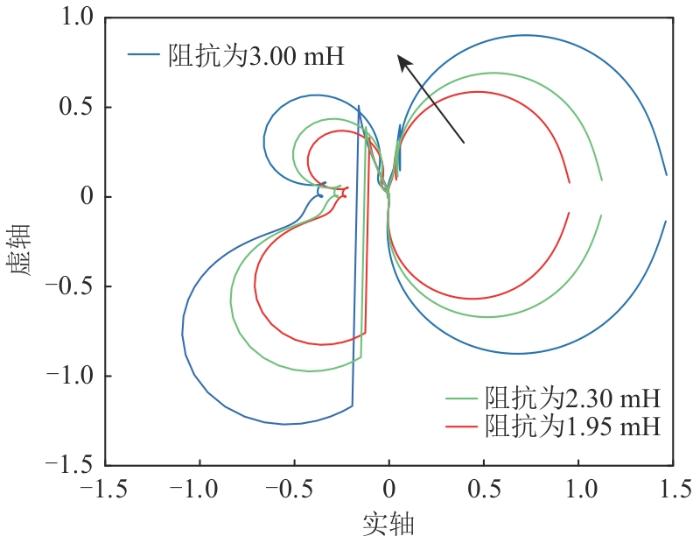
为验证本文所提控制策略的有效性,需分析改进LADRC策略下线路阻抗值对网侧变流器并网系统稳定性的影响。
根据文献[17 ]可知,若阻抗比环路增益矩阵的2条特征值曲线满足Nyquist判据时,则系统是稳定的。阻抗比特征值l 1 、 l 2
l 1 ( s ) = X ( s ) + X 2 ( s ) + 4 L p n ( s ) L n p ( s ) 2 (29)
l 2 ( s ) = X ( s ) - X 2 ( s ) + 4 L p n ( s ) L n p ( s ) 2 (30)
式中:X ( s ) = L p p ( s ) + L n n ( s ) L p p ( s ) L p n ( s ) L n p ( s ) L n n ( s )
选取同4.2节的阻抗值绘制Nyquist曲线如图6 所示,图中箭头方向代表阻抗增大。可以看出,改进LADRC控制下Nyquist曲线未包围(-1, 0)点,并网系统是稳定的,但随着线路阻抗的增大,改进LADRC控制下的Nyquist曲线与(-1, 0)点之间的距离在减小,SSO风险增大,表明线路阻抗值增加对网侧变流器并网系统的稳定性有影响。
图6
图6
改进LADRC控制下Nyquist曲线
Fig. 6
Nyquist curve under the control of improved LADRC
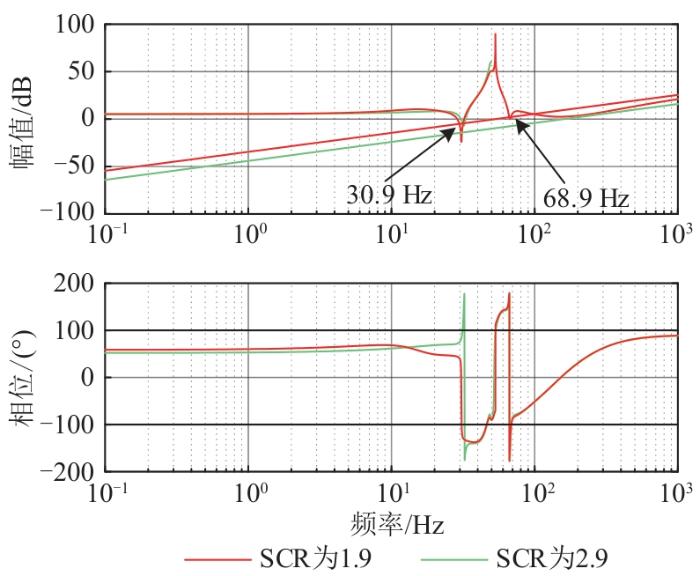
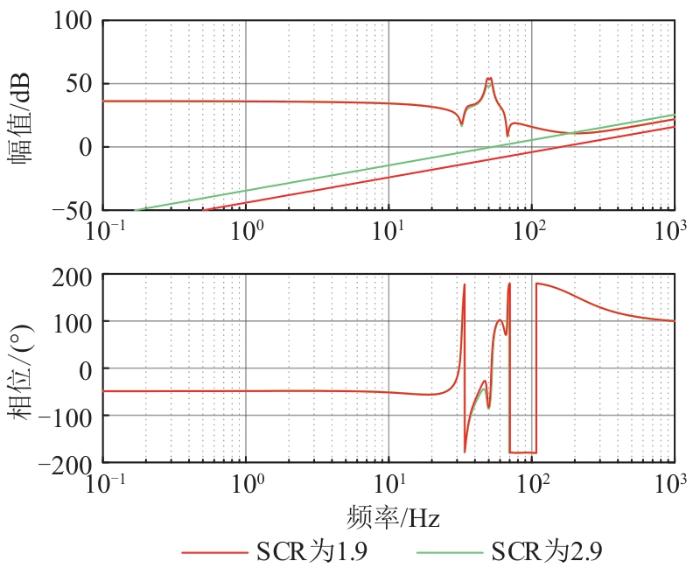
分别取线路阻抗3、1.95 mH(对应SCR分别为1.9、2.9),代入式(25),分析不同控制方法下线路阻抗值对网侧变换器并网系统稳定性的影响[17 -18 ,24 ] 。图7 为传统LADRC阻抗伯德图,可见,当处于弱电网时,线路阻抗与网侧变换器阻抗幅值无交点,表明在该工况下采用传统LADRC控制策略时并网系统稳定运行;但处于极弱电网工况时,线路阻抗与网侧变换器阻抗幅值在30.9 Hz与68.9 Hz处均有交点,对应的相频特性位于负阻尼区,表明网侧变换器并网系统在该工况下采用传统LADRC控制策略存在次/超同步振荡风险。图8 为改进LADRC阻抗伯德图,可以发现,当处于极弱电网与弱电网工况时,线路阻抗与网侧变换器阻抗幅值无交点,表明在采用改进LADRC控制策略时并网系统稳定运行。
图7
图7
传统LADRC阻抗伯德图
Fig. 7
Traditional LADRC impedance Bode diagram
图8
图8
改进LADRC阻抗伯德图
Fig. 8
Improved LADRC impedance Bode diagram
5 仿真验证分析
5.1 系统主要参数
文献[12 ,18 ]揭示了PI控制器参数对直驱风机SSO影响较为明显,为了验证前文所提出改进LADRC电流内环控制器,在PSCAD/EMTDC中建立如图1 所示的等值仿真模型进行验证,将3种不同的控制策略进行对比。其仿真模型参数如表2 所示。
5.2 相同风速不、同短路比仿真对比
交流电网强度越小,SSO越剧烈[12 ] 。文献[25 ]提出电网强度用短路电流比来描述,定义短路电流比≤3的电网为弱电网,短路电流比<2的电网为极弱电网,设置不同的SCR进行仿真分析。
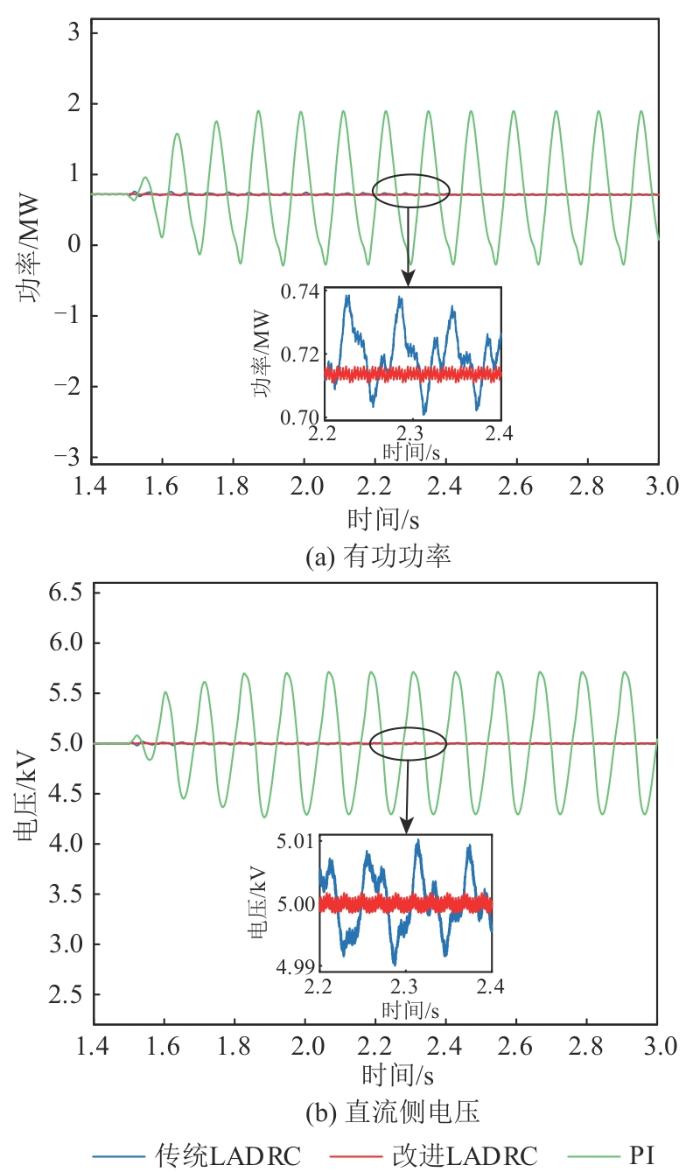
1)设置SCR为1.9、t =1.5 s时系统接入弱电网,其等效电感为L =0.003 H。图9 为SCR为1.9时,3种控制策略下系统有功功率、直流侧电压对比图。
图9
图9
SCR为1.9时对比图
Fig. 9
Comparison chart when SCR is 1.9
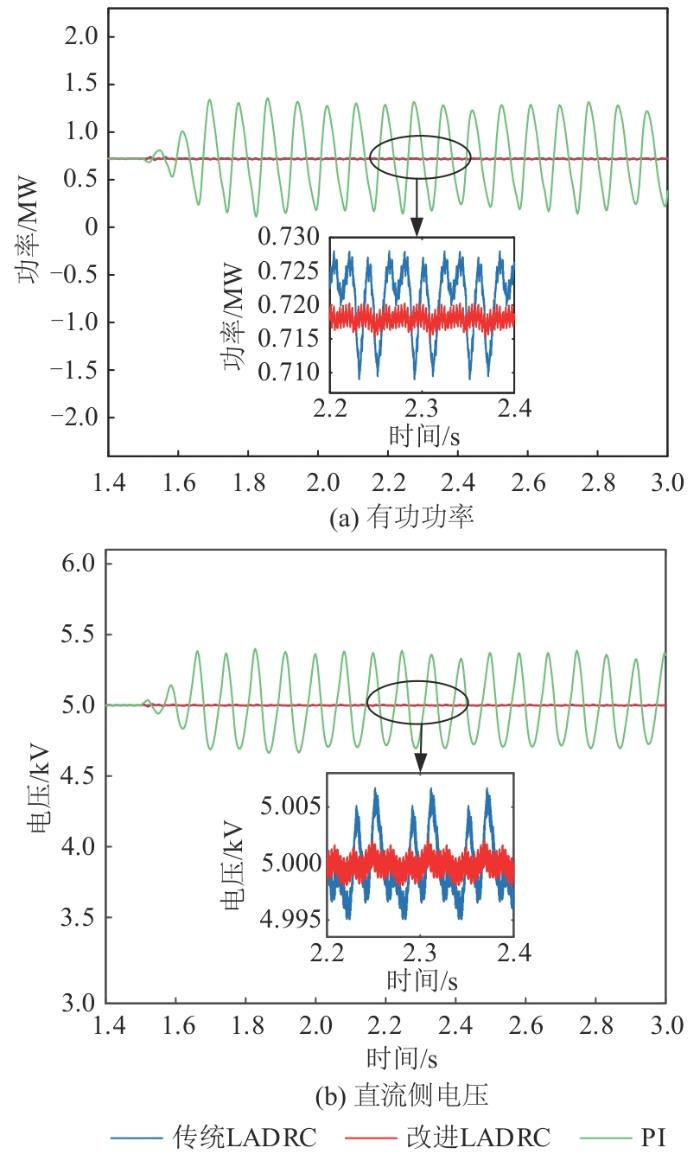
2)设置SCR为2.9、t =1.5 s时系统接入弱电网,其等效电感为L =0.001 95 H。图10 为SCR为2.9时3种控制策略下系统有功功率、直流侧电压对比图。
图10
图10
SCR为2.9时3种控制对比图
SCR is 2.9
Fig. 10
Comparison chart of three controls when
表3 为风速为7.5 m/s时不同SCR下直流侧电压和有功功率围,由图9 、10 和表3 可知,采用传统LADRC和改进LADRC都可以抑制SSO,而PI控制器在低风速下很难抑制SSO。参考表3 数据可知,改进LADRC可以更好地减小跟踪误差、缩小功率波动范围。
5.3 不同风速、相同短路比仿真对比
低风速情况下SSO易发生的概率较大,风速越低,系统稳定性越差[26 ] 。结合实际工况,设置SCR为2.5,通过调节等效电流源电流的大小来设置不同的风速进行仿真分析。
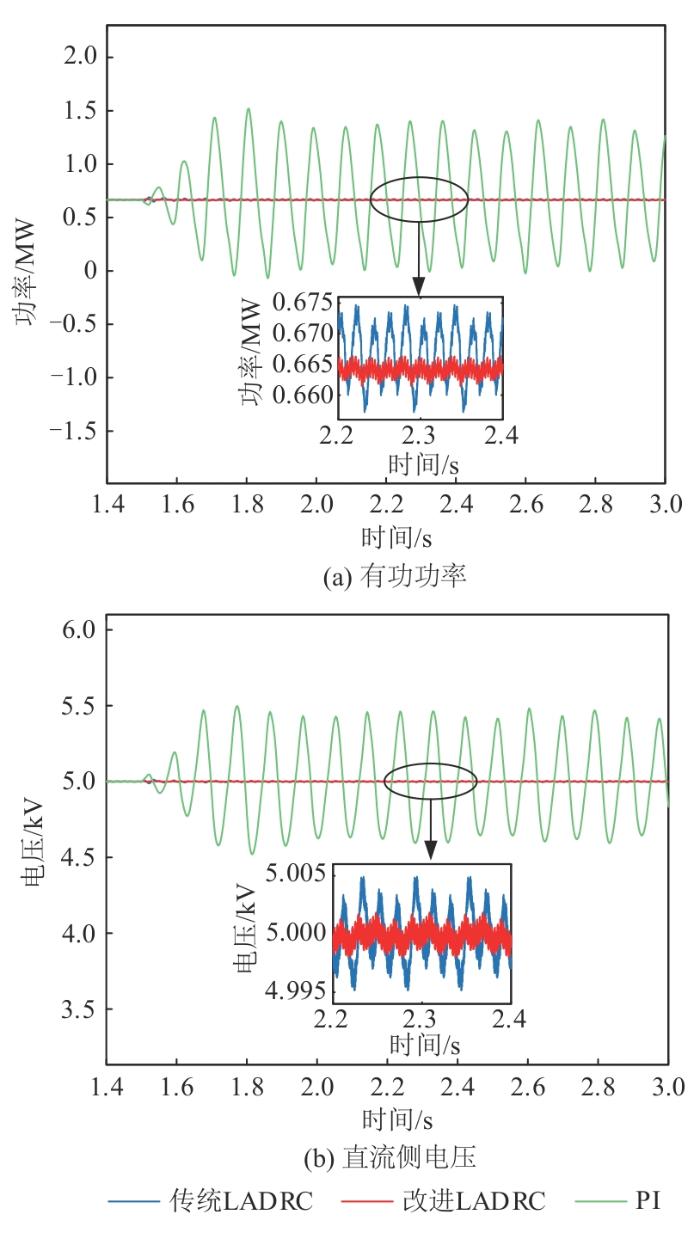
1)设置风速为7.3 m/s、t =1.5 s时系统接入弱电网。图11 为风速为7.3 m/s时,3种控制策略下系统有功功率、直流侧电压对比图。
图11
图11
风速为7.3 m/s时对比图
Fig.11
Comparison chart when wind speed is 7.3 m/s
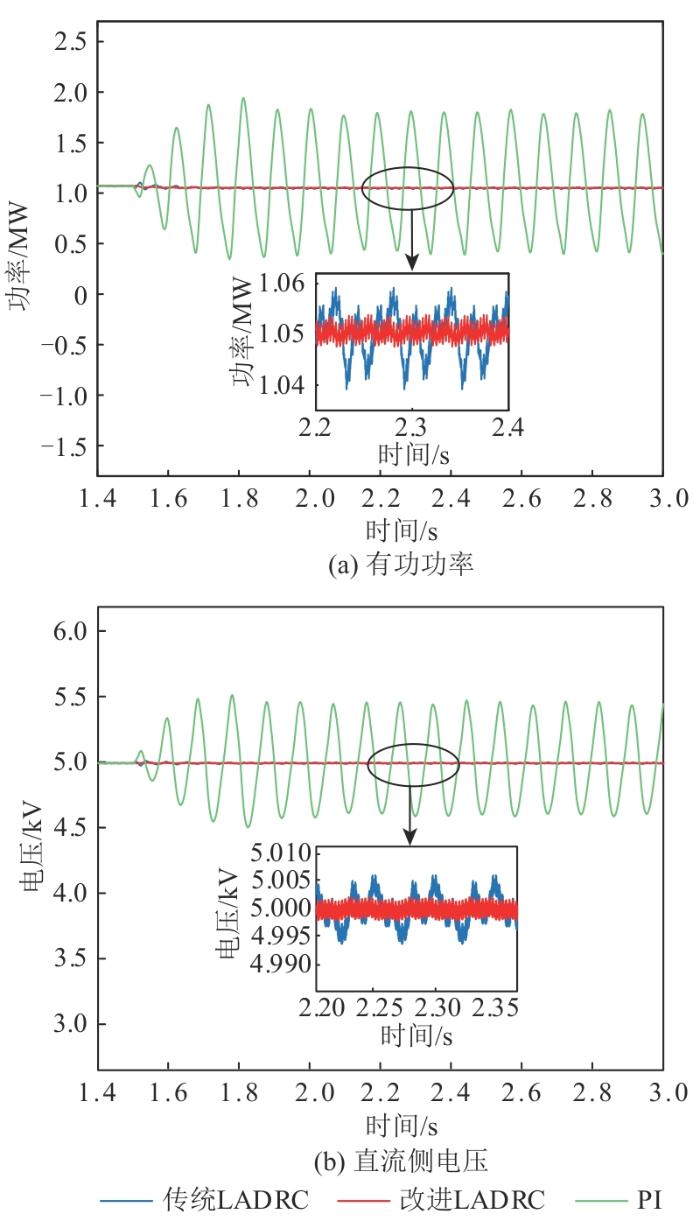
2)设置风速为8.5 m/s、t =1.5 s时系统接入弱电网。图12 为风速为8.5 m/s时,3种控制策略下系统有功功率、直流侧电压对比图。
图12
图12
风速为8.5 m/s时对比图
Fig. 12
Comparison chart when wind speed is 8.5 m/s
表4 为SCR为2.5时不同风速数据波动范围。由图11 、12 和表4 可知:采用传统LADRC和改进LADRC都可以抑制SSO,而PI控制在弱电网下不能抑制。
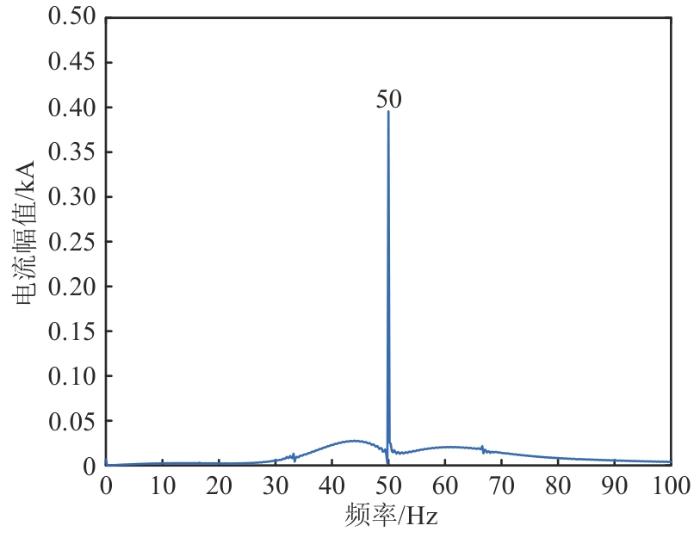
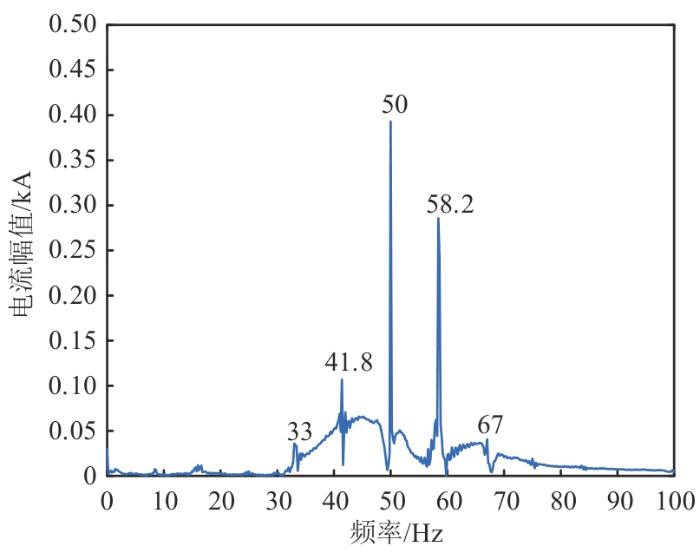
在SCR为1.9时的弱电网工况下,分别采用改进LADRC电流内环控制器和电流内环PI控制器,进行A相电流进行频谱分析,结果分别如图13 、14 所示。从图13 中可以看出,A相电流仅包含50 Hz工频分量。从图14 中可以看出,A相电流不仅含有50 Hz工频分量,还含有2组其他次/超同步分量。显然,改进LADRC电流内环控制器可以有效消除次同步分量,从而达到抑制SSO的效果。
图13
图13
改进LADRC控制FFT分析
Fig. 13
Improved LADRC control FFT analysis
图14
图14
PI控制FFT分析
Fig. 14
PI control FFT analysis
6 结论
以直驱式风电机组接入弱电网引发SSO为研究对象,从而建立网侧变流器数学模型,提出改进LSEF的LADRC控制策略。主要结论如下:
1)与传统LADRC控制器相比,改进LADRC控制器可以更好地缩小功率波动范围、直流侧电压波动范围,减小跟踪误差。
2)线路阻抗对并网系统稳定性有重要影响,阻抗值越大,SSO风险越大。
参考文献
View Option
[1]
[本文引用: 1]
YU Y J WANG L C ZHANG M Y et al Stability criterion of subsynchronous oscillation of direct drive permanent magnet synchronous generator based on impedance polynomial fitting
[J].Power Generation Technology ,2020 ,41 (4 ):429 -436 . doi:10.12096/j.2096-4528.pgt.19140
[本文引用: 1]
[2]
KANG J L YU H DUAN Y et al Equivalent modeling method of sub-synchronous oscillation in wind farm
[J].Power Generation Technology ,2022 ,43 (6 ):880 -891 . doi:10.12096/j.2096-4528.pgt.21121
[3]
王俊茜 ,贾祺 ,刘侃 ,等 混合风电场接入含固定串补系统的次同步振荡特性分析
[J].可再生能源 ,2022 ,40 (5 ):651 -659 .
WANG J X JIA Q LIU K et al Analysis of subsynchronous oscillation characteristics of hybrid-based wind farm connected with fixed series compensation system
[J].Renewable Energy Resources ,2022 ,40 (5 ):651 -659 .
[4]
李博浩 ,郭昆丽 ,吕家君 ,等 次同步电流双通道附加阻尼抑制次同步振荡策略及阻抗模型分析
[J].分布式能源 ,2023 ,8 (6 ):1 -10 .
LI B H GUO K L LÜ J J et al Subsynchronous current dual channel additional damping suppression subsynchronous oscillation strategy and impedance model analysis
[J].Distributed Energy ,2023 ,8 (6 ):1 -10 .
[5]
戴礼国 ,杨浩 ,陈力 ,等 基于深度强化学习的风电柔直并网系统次同步振荡抑制方法
[J].智慧电力 ,2023 ,51 (4 ):1 -7 .
[本文引用: 1]
DAI L G YANG H CHEN L et al Subsynchronous oscillation suppression method for flexible direct grid-connected wind power system based on deep reinforcement learning
[J].Smart Power ,2023 ,51 (4 ):1 -7 .
[本文引用: 1]
[6]
LIU H BI T CHANG X et al Impacts of subsynchronous and supersynchronous frequency components on synchrophasor measurements
[J].Journal of Modern Power Systems and Clean Energy ,2016 ,4 (3 ):362 -369 . doi:10.1007/s40565-016-0225-4
[本文引用: 1]
[7]
高本锋 ,刘晋 ,李忍 ,等 风电机组的次同步控制相互作用研究综述
[J].电工技术学报 ,2015 ,30 (16 ):154 -161 .
[本文引用: 1]
GAO B F LIU J LI R et al Studies of sub-synchronous control interaction in wind turbine generators
[J].Transactions of China Electrotechnical Society ,2015 ,30 (16 ):154 -161 .
[本文引用: 1]
[8]
VIRULKAR V B GOTMARE G V Sub-synchronous resonance in series compensated wind farm:a review
[J].Renewable and Sustainable Energy Reviews ,2016 ,55 :1010 -1029 . doi:10.1016/j.rser.2015.11.012
[本文引用: 1]
[9]
HUANG B Y SUN H S LIU Y M Study on subsynchronous oscillation in D-PMSGs-based wind farm integrated to power system
[J].IET Renewable Power Gener ,2019 ,13 (1 ):16 -26 . doi:10.1049/iet-rpg.2018.5051
[本文引用: 1]
[10]
陈晨 ,杜文娟 ,王海风 风电场接入引发电力系统次同步振荡机理综述
[J].南方电网技术 ,2018 ,12 (1 ):84 -93 .
CHEN C DU W J WANG H F A review of the subsynchronous oscillation mechanism of the power system caused by the connection of wind farms
[J].China Southern Power Grid Technology ,2018 ,12 (1 ):84 -93 .
[11]
LIU H XIE X HE J et al Subsynchronous interaction between direct-drive PMSG based wind farms and weak AC networks
[J].IEEE Transactions on Power Systems ,2017 ,32 (6 ):4708 -4720 . doi:10.1109/tpwrs.2017.2682197
[本文引用: 1]
[12]
徐衍会 ,曹宇平 直驱风机网侧换流器引发次/超同步振荡机理研究
[J].电网技术 ,2018 ,42 (5 ):1556 -1564 .
[本文引用: 3]
XU Y H CAO Y P Research on mechanism of sub/sup-synchronous oscillation caused by GSC controller of direct-drive permanent magnetic synchronous generator
[J].Power System Technology ,2018 ,42 (5 ):1556 -1564 .
[本文引用: 3]
[13]
易友川 直驱风电场接入弱交流电网的次同步振荡分析及抑制策略研究
[D].保定 :华北电力大学 ,2021 .
[本文引用: 1]
YI Y C Sub-synchronous oscillation analysis and suppression strategy research of direct-driven wind farm connected to weak AC power grid
[D].Baoding :North China Electric Power University ,2021 .
[本文引用: 1]
[14]
杨霞 风电并网逆变器双闭环控制系统的研究
[D].天津 :天津理工大学 ,2021 .
[本文引用: 1]
YANG X Research on double closed-loop control system of wind power grid-connected inverter
[D].Tianjin :Tianjin University of Technology ,2021 .
[本文引用: 1]
[15]
蔡维正 ,郭昆丽 ,刘璐雨 ,等 基于一阶LADRC控制的直驱风机次同步振荡抑制策略
[J].中国电力 ,2022 ,55 (4 ):175 -184 .
[本文引用: 1]
CAI W Z GUO K L LIU L Y et al Subsynchronous oscillation mitigation strategy based on first-order LADRC for direct-drive wind turbines
[J].Electric Power ,2022 ,55 (4 ):175 -184 .
[本文引用: 1]
[16]
李博浩 ,郭昆丽 ,吕家君 ,等 弱电网下改进LADRC抑制直驱风机次同步振荡研究
[J].中国电力 ,2023 ,56 (4 ):56 -67 .
[本文引用: 2]
LI B H GUO K L LÜ J J et al Inhibition of subsynchronous oscillation of direct-drive wind turbine by improved LADRC in weak grids
[J].Electric Power ,2023 ,56 (4 ):56 -67 .
[本文引用: 2]
[17]
郑国强 考虑频率耦合特性的并网逆变器阻抗特性与稳定性研究
[D].兰州 :兰州理工大学 ,2021 .
[本文引用: 3]
ZHENG G Q Study on impedance characteristics and stability of grid-connected inverter considering frequency coupling characteristics
[D].Lanzhou :Lanzhou University of Technology ,2021 .
[本文引用: 3]
[18]
彭上 自抗扰并网逆变器宽频带阻抗建模与稳定性对比分析研究
[D].长沙 :湖南大学 ,2020 .
[本文引用: 3]
PENG S Broadband impedance modeling and stability comparative analysis of ADRC grid-connected inverter
[D].Changsha :Hunan University ,2020 .
[本文引用: 3]
[19]
韩京清 自抗扰控制技术:估计补偿不确定因素的控制技术 [M].北京 :国防工业出版社 ,2008 .
[本文引用: 1]
HAN J Q Active disturbance rejection control technique [M].Beijing :National Defense Industry Press ,2008 .
[本文引用: 1]
[20]
CAO Y ZHAO Q YE Y et al ADRC-based current control for grid-tied inverters:design,analysis,and verification
[J].IEEE Transactions on industrial electronics ,2019 ,67 (10 ):8428 -8437 . doi:10.1109/tie.2019.2949513
[本文引用: 1]
[21]
苏步芸 ,王诗超 新型电力系统背景下新能源送出合理消纳率研究
[J].南方能源建设 ,2023 ,10 (6 ):43 -50 .
[本文引用: 1]
SU B Y WANG S C Research on reasonable consumption rate of new energy transmission under the new power system
[J].Southern Energy Construction ,2023 ,10 (6 ):43 -50 .
[本文引用: 1]
[22]
VIETO I SUN J Sequence impedance modeling and converter-grid resonance analysis considering DC bus dynamics and mirrored harmonics
[C]∥Proceedings of 2018 IEEE 19th Workshop on Control and Modeling for Power Electronics (CO-MPEL) .Padua,Italy :IEEE ,2018 :1 -8 . doi:10.1109/compel.2018.8458498
[本文引用: 2]
[23]
李光辉 ,王伟胜 ,刘纯 ,等 直驱风电场接入弱电网宽频带振荡机理与抑制方法(一):宽频带阻抗特性与振荡机理分析
[J].中国电机工程学报 ,2019 ,39 (22 ):6547 -6561 .
[本文引用: 1]
LI G H WANG W S LIU C et al Mechanism analysis and suppression method of wideband oscillation of PMSG wind farms connected to weak grid (part Ⅰ):analysis of wideband impedance characteristics and oscillation mechanism
[J].Proceedings of the CSEE ,2019 ,39 (22 ):6547 -6561 .
[本文引用: 1]
[24]
范丽霞 ,蔡瑞强 ,张欢畅 ,等 电压型虚拟同步发电机控制策略下的双馈风电机组阻抗及次同步振荡特性
[J].发电技术 ,2019 ,40 (5 ):434 -439 .
[本文引用: 2]
FAN L X CAI R Q ZHANG H C et al Impedance and sub-synchronous oscillation characteristics of doubly-fed induction generators with control strategy of voltage virtual synchronous generator
[J].Power Generation Technology ,2019 ,40 (5 ):434 -439 .
[本文引用: 2]
[25]
COMMITTEE D IEEE guide for planning DC links terminating at AC locations having low short circuit capacities [S].IEEE Standards,1997 :1204 -1227 .
[本文引用: 1]
[26]
王亮 ,谢小荣 ,姜齐荣 ,等 大规模双馈风电场次同步谐振的分析与抑制
[J].电力系统自动化 ,2014 ,38 (22 ):26 -31 .
[本文引用: 1]
WANG L XIE X R JIANG Q R et al Analysis and mitigation of SSR problems in large-scale wind farms with doubly-fed wind turbines
[J].Automation of Electric Power Systems ,2014 ,38 (22 ):26 -31 .
[本文引用: 1]
基于阻抗特性多项式拟合的直驱风电机组次同步振荡稳定判据
1
2020
... 随着风电大量接入电网,其诱发的次同步振荡(subsynchronous oscillation,SSO)现象对电力系统安全稳定运行构成了严重的威胁[1 -5 ] .2015年新疆哈密地区大规模直驱风电机组出现次同步振荡[6 ] ,给电网稳定运行造成重要影响. ...
Stability criterion of subsynchronous oscillation of direct drive permanent magnet synchronous generator based on impedance polynomial fitting
1
2020
... 随着风电大量接入电网,其诱发的次同步振荡(subsynchronous oscillation,SSO)现象对电力系统安全稳定运行构成了严重的威胁[1 -5 ] .2015年新疆哈密地区大规模直驱风电机组出现次同步振荡[6 ] ,给电网稳定运行造成重要影响. ...
Equivalent modeling method of sub-synchronous oscillation in wind farm
0
2022
混合风电场接入含固定串补系统的次同步振荡特性分析
0
2022
Analysis of subsynchronous oscillation characteristics of hybrid-based wind farm connected with fixed series compensation system
0
2022
次同步电流双通道附加阻尼抑制次同步振荡策略及阻抗模型分析
0
2023
Subsynchronous current dual channel additional damping suppression subsynchronous oscillation strategy and impedance model analysis
0
2023
基于深度强化学习的风电柔直并网系统次同步振荡抑制方法
1
2023
... 随着风电大量接入电网,其诱发的次同步振荡(subsynchronous oscillation,SSO)现象对电力系统安全稳定运行构成了严重的威胁[1 -5 ] .2015年新疆哈密地区大规模直驱风电机组出现次同步振荡[6 ] ,给电网稳定运行造成重要影响. ...
Subsynchronous oscillation suppression method for flexible direct grid-connected wind power system based on deep reinforcement learning
1
2023
... 随着风电大量接入电网,其诱发的次同步振荡(subsynchronous oscillation,SSO)现象对电力系统安全稳定运行构成了严重的威胁[1 -5 ] .2015年新疆哈密地区大规模直驱风电机组出现次同步振荡[6 ] ,给电网稳定运行造成重要影响. ...
Impacts of subsynchronous and supersynchronous frequency components on synchrophasor measurements
1
2016
... 随着风电大量接入电网,其诱发的次同步振荡(subsynchronous oscillation,SSO)现象对电力系统安全稳定运行构成了严重的威胁[1 -5 ] .2015年新疆哈密地区大规模直驱风电机组出现次同步振荡[6 ] ,给电网稳定运行造成重要影响. ...
风电机组的次同步控制相互作用研究综述
1
2015
... 为此,学者们对直驱风机并网诱发SSO问题进行了广泛的研究.文献[7 -8 ]针对风电机组的次同步振荡问题,从特性、分析方法和抑制措施等方面进行了综述.文献[9 -11 ]研究指出,直驱风电机组并入弱电网诱发SSO现象的主要因素之一是网侧变流器与电网之间的交互作用.文献[12 ]研究表明,直驱风机控制系统锁相环参数、电流内环参数对SSO有明显的影响.文献[13 ]用自抗扰控制(active disturbance rejection control,ADRC)替换电流内环PI控制器,并阐述ADRC抑制SSO原理,但其控制器参数整定过于繁琐.文献[14 ]建立直驱式风机并网变流器数学模型,用线性自抗扰控制(linear active disturbance rejection control,ADRC)替换电流内环PI控制器,简化了控制器参数整定的难度.文献[15 ]提出一阶LADRC电流内环控制器设计,可抵消线路中的次同步频率分量,虽能有效抑制SSO现象,但存在较大的误差与超调量.文献[16 ]提出基于一阶总扰动偏差控制的微分前馈LADRC,该控制器不仅可以减小跟踪误差且具有较强的抗干扰性能,但其不足之处在于功率波动范围较大.文献[17 ]在dq 坐标系下建立了网侧变流器的阻抗模型,并结合广义Nyquist判据对风电并网系统稳定性影响因素进行了分析.文献[18 ]分析了接入电网强度对并网系统稳定性的影响. ...
Studies of sub-synchronous control interaction in wind turbine generators
1
2015
... 为此,学者们对直驱风机并网诱发SSO问题进行了广泛的研究.文献[7 -8 ]针对风电机组的次同步振荡问题,从特性、分析方法和抑制措施等方面进行了综述.文献[9 -11 ]研究指出,直驱风电机组并入弱电网诱发SSO现象的主要因素之一是网侧变流器与电网之间的交互作用.文献[12 ]研究表明,直驱风机控制系统锁相环参数、电流内环参数对SSO有明显的影响.文献[13 ]用自抗扰控制(active disturbance rejection control,ADRC)替换电流内环PI控制器,并阐述ADRC抑制SSO原理,但其控制器参数整定过于繁琐.文献[14 ]建立直驱式风机并网变流器数学模型,用线性自抗扰控制(linear active disturbance rejection control,ADRC)替换电流内环PI控制器,简化了控制器参数整定的难度.文献[15 ]提出一阶LADRC电流内环控制器设计,可抵消线路中的次同步频率分量,虽能有效抑制SSO现象,但存在较大的误差与超调量.文献[16 ]提出基于一阶总扰动偏差控制的微分前馈LADRC,该控制器不仅可以减小跟踪误差且具有较强的抗干扰性能,但其不足之处在于功率波动范围较大.文献[17 ]在dq 坐标系下建立了网侧变流器的阻抗模型,并结合广义Nyquist判据对风电并网系统稳定性影响因素进行了分析.文献[18 ]分析了接入电网强度对并网系统稳定性的影响. ...
Sub-synchronous resonance in series compensated wind farm:a review
1
2016
... 为此,学者们对直驱风机并网诱发SSO问题进行了广泛的研究.文献[7 -8 ]针对风电机组的次同步振荡问题,从特性、分析方法和抑制措施等方面进行了综述.文献[9 -11 ]研究指出,直驱风电机组并入弱电网诱发SSO现象的主要因素之一是网侧变流器与电网之间的交互作用.文献[12 ]研究表明,直驱风机控制系统锁相环参数、电流内环参数对SSO有明显的影响.文献[13 ]用自抗扰控制(active disturbance rejection control,ADRC)替换电流内环PI控制器,并阐述ADRC抑制SSO原理,但其控制器参数整定过于繁琐.文献[14 ]建立直驱式风机并网变流器数学模型,用线性自抗扰控制(linear active disturbance rejection control,ADRC)替换电流内环PI控制器,简化了控制器参数整定的难度.文献[15 ]提出一阶LADRC电流内环控制器设计,可抵消线路中的次同步频率分量,虽能有效抑制SSO现象,但存在较大的误差与超调量.文献[16 ]提出基于一阶总扰动偏差控制的微分前馈LADRC,该控制器不仅可以减小跟踪误差且具有较强的抗干扰性能,但其不足之处在于功率波动范围较大.文献[17 ]在dq 坐标系下建立了网侧变流器的阻抗模型,并结合广义Nyquist判据对风电并网系统稳定性影响因素进行了分析.文献[18 ]分析了接入电网强度对并网系统稳定性的影响. ...
Study on subsynchronous oscillation in D-PMSGs-based wind farm integrated to power system
1
2019
... 为此,学者们对直驱风机并网诱发SSO问题进行了广泛的研究.文献[7 -8 ]针对风电机组的次同步振荡问题,从特性、分析方法和抑制措施等方面进行了综述.文献[9 -11 ]研究指出,直驱风电机组并入弱电网诱发SSO现象的主要因素之一是网侧变流器与电网之间的交互作用.文献[12 ]研究表明,直驱风机控制系统锁相环参数、电流内环参数对SSO有明显的影响.文献[13 ]用自抗扰控制(active disturbance rejection control,ADRC)替换电流内环PI控制器,并阐述ADRC抑制SSO原理,但其控制器参数整定过于繁琐.文献[14 ]建立直驱式风机并网变流器数学模型,用线性自抗扰控制(linear active disturbance rejection control,ADRC)替换电流内环PI控制器,简化了控制器参数整定的难度.文献[15 ]提出一阶LADRC电流内环控制器设计,可抵消线路中的次同步频率分量,虽能有效抑制SSO现象,但存在较大的误差与超调量.文献[16 ]提出基于一阶总扰动偏差控制的微分前馈LADRC,该控制器不仅可以减小跟踪误差且具有较强的抗干扰性能,但其不足之处在于功率波动范围较大.文献[17 ]在dq 坐标系下建立了网侧变流器的阻抗模型,并结合广义Nyquist判据对风电并网系统稳定性影响因素进行了分析.文献[18 ]分析了接入电网强度对并网系统稳定性的影响. ...
风电场接入引发电力系统次同步振荡机理综述
0
2018
A review of the subsynchronous oscillation mechanism of the power system caused by the connection of wind farms
0
2018
Subsynchronous interaction between direct-drive PMSG based wind farms and weak AC networks
1
2017
... 为此,学者们对直驱风机并网诱发SSO问题进行了广泛的研究.文献[7 -8 ]针对风电机组的次同步振荡问题,从特性、分析方法和抑制措施等方面进行了综述.文献[9 -11 ]研究指出,直驱风电机组并入弱电网诱发SSO现象的主要因素之一是网侧变流器与电网之间的交互作用.文献[12 ]研究表明,直驱风机控制系统锁相环参数、电流内环参数对SSO有明显的影响.文献[13 ]用自抗扰控制(active disturbance rejection control,ADRC)替换电流内环PI控制器,并阐述ADRC抑制SSO原理,但其控制器参数整定过于繁琐.文献[14 ]建立直驱式风机并网变流器数学模型,用线性自抗扰控制(linear active disturbance rejection control,ADRC)替换电流内环PI控制器,简化了控制器参数整定的难度.文献[15 ]提出一阶LADRC电流内环控制器设计,可抵消线路中的次同步频率分量,虽能有效抑制SSO现象,但存在较大的误差与超调量.文献[16 ]提出基于一阶总扰动偏差控制的微分前馈LADRC,该控制器不仅可以减小跟踪误差且具有较强的抗干扰性能,但其不足之处在于功率波动范围较大.文献[17 ]在dq 坐标系下建立了网侧变流器的阻抗模型,并结合广义Nyquist判据对风电并网系统稳定性影响因素进行了分析.文献[18 ]分析了接入电网强度对并网系统稳定性的影响. ...
直驱风机网侧换流器引发次/超同步振荡机理研究
3
2018
... 为此,学者们对直驱风机并网诱发SSO问题进行了广泛的研究.文献[7 -8 ]针对风电机组的次同步振荡问题,从特性、分析方法和抑制措施等方面进行了综述.文献[9 -11 ]研究指出,直驱风电机组并入弱电网诱发SSO现象的主要因素之一是网侧变流器与电网之间的交互作用.文献[12 ]研究表明,直驱风机控制系统锁相环参数、电流内环参数对SSO有明显的影响.文献[13 ]用自抗扰控制(active disturbance rejection control,ADRC)替换电流内环PI控制器,并阐述ADRC抑制SSO原理,但其控制器参数整定过于繁琐.文献[14 ]建立直驱式风机并网变流器数学模型,用线性自抗扰控制(linear active disturbance rejection control,ADRC)替换电流内环PI控制器,简化了控制器参数整定的难度.文献[15 ]提出一阶LADRC电流内环控制器设计,可抵消线路中的次同步频率分量,虽能有效抑制SSO现象,但存在较大的误差与超调量.文献[16 ]提出基于一阶总扰动偏差控制的微分前馈LADRC,该控制器不仅可以减小跟踪误差且具有较强的抗干扰性能,但其不足之处在于功率波动范围较大.文献[17 ]在dq 坐标系下建立了网侧变流器的阻抗模型,并结合广义Nyquist判据对风电并网系统稳定性影响因素进行了分析.文献[18 ]分析了接入电网强度对并网系统稳定性的影响. ...
... 文献[12 ,18 ]揭示了PI控制器参数对直驱风机SSO影响较为明显,为了验证前文所提出改进LADRC电流内环控制器,在PSCAD/EMTDC中建立如图1 所示的等值仿真模型进行验证,将3种不同的控制策略进行对比.其仿真模型参数如表2 所示. ...
... 交流电网强度越小,SSO越剧烈[12 ] .文献[25 ]提出电网强度用短路电流比来描述,定义短路电流比≤3的电网为弱电网,短路电流比<2的电网为极弱电网,设置不同的SCR进行仿真分析. ...
Research on mechanism of sub/sup-synchronous oscillation caused by GSC controller of direct-drive permanent magnetic synchronous generator
3
2018
... 为此,学者们对直驱风机并网诱发SSO问题进行了广泛的研究.文献[7 -8 ]针对风电机组的次同步振荡问题,从特性、分析方法和抑制措施等方面进行了综述.文献[9 -11 ]研究指出,直驱风电机组并入弱电网诱发SSO现象的主要因素之一是网侧变流器与电网之间的交互作用.文献[12 ]研究表明,直驱风机控制系统锁相环参数、电流内环参数对SSO有明显的影响.文献[13 ]用自抗扰控制(active disturbance rejection control,ADRC)替换电流内环PI控制器,并阐述ADRC抑制SSO原理,但其控制器参数整定过于繁琐.文献[14 ]建立直驱式风机并网变流器数学模型,用线性自抗扰控制(linear active disturbance rejection control,ADRC)替换电流内环PI控制器,简化了控制器参数整定的难度.文献[15 ]提出一阶LADRC电流内环控制器设计,可抵消线路中的次同步频率分量,虽能有效抑制SSO现象,但存在较大的误差与超调量.文献[16 ]提出基于一阶总扰动偏差控制的微分前馈LADRC,该控制器不仅可以减小跟踪误差且具有较强的抗干扰性能,但其不足之处在于功率波动范围较大.文献[17 ]在dq 坐标系下建立了网侧变流器的阻抗模型,并结合广义Nyquist判据对风电并网系统稳定性影响因素进行了分析.文献[18 ]分析了接入电网强度对并网系统稳定性的影响. ...
... 文献[12 ,18 ]揭示了PI控制器参数对直驱风机SSO影响较为明显,为了验证前文所提出改进LADRC电流内环控制器,在PSCAD/EMTDC中建立如图1 所示的等值仿真模型进行验证,将3种不同的控制策略进行对比.其仿真模型参数如表2 所示. ...
... 交流电网强度越小,SSO越剧烈[12 ] .文献[25 ]提出电网强度用短路电流比来描述,定义短路电流比≤3的电网为弱电网,短路电流比<2的电网为极弱电网,设置不同的SCR进行仿真分析. ...
直驱风电场接入弱交流电网的次同步振荡分析及抑制策略研究
1
2021
... 为此,学者们对直驱风机并网诱发SSO问题进行了广泛的研究.文献[7 -8 ]针对风电机组的次同步振荡问题,从特性、分析方法和抑制措施等方面进行了综述.文献[9 -11 ]研究指出,直驱风电机组并入弱电网诱发SSO现象的主要因素之一是网侧变流器与电网之间的交互作用.文献[12 ]研究表明,直驱风机控制系统锁相环参数、电流内环参数对SSO有明显的影响.文献[13 ]用自抗扰控制(active disturbance rejection control,ADRC)替换电流内环PI控制器,并阐述ADRC抑制SSO原理,但其控制器参数整定过于繁琐.文献[14 ]建立直驱式风机并网变流器数学模型,用线性自抗扰控制(linear active disturbance rejection control,ADRC)替换电流内环PI控制器,简化了控制器参数整定的难度.文献[15 ]提出一阶LADRC电流内环控制器设计,可抵消线路中的次同步频率分量,虽能有效抑制SSO现象,但存在较大的误差与超调量.文献[16 ]提出基于一阶总扰动偏差控制的微分前馈LADRC,该控制器不仅可以减小跟踪误差且具有较强的抗干扰性能,但其不足之处在于功率波动范围较大.文献[17 ]在dq 坐标系下建立了网侧变流器的阻抗模型,并结合广义Nyquist判据对风电并网系统稳定性影响因素进行了分析.文献[18 ]分析了接入电网强度对并网系统稳定性的影响. ...
Sub-synchronous oscillation analysis and suppression strategy research of direct-driven wind farm connected to weak AC power grid
1
2021
... 为此,学者们对直驱风机并网诱发SSO问题进行了广泛的研究.文献[7 -8 ]针对风电机组的次同步振荡问题,从特性、分析方法和抑制措施等方面进行了综述.文献[9 -11 ]研究指出,直驱风电机组并入弱电网诱发SSO现象的主要因素之一是网侧变流器与电网之间的交互作用.文献[12 ]研究表明,直驱风机控制系统锁相环参数、电流内环参数对SSO有明显的影响.文献[13 ]用自抗扰控制(active disturbance rejection control,ADRC)替换电流内环PI控制器,并阐述ADRC抑制SSO原理,但其控制器参数整定过于繁琐.文献[14 ]建立直驱式风机并网变流器数学模型,用线性自抗扰控制(linear active disturbance rejection control,ADRC)替换电流内环PI控制器,简化了控制器参数整定的难度.文献[15 ]提出一阶LADRC电流内环控制器设计,可抵消线路中的次同步频率分量,虽能有效抑制SSO现象,但存在较大的误差与超调量.文献[16 ]提出基于一阶总扰动偏差控制的微分前馈LADRC,该控制器不仅可以减小跟踪误差且具有较强的抗干扰性能,但其不足之处在于功率波动范围较大.文献[17 ]在dq 坐标系下建立了网侧变流器的阻抗模型,并结合广义Nyquist判据对风电并网系统稳定性影响因素进行了分析.文献[18 ]分析了接入电网强度对并网系统稳定性的影响. ...
风电并网逆变器双闭环控制系统的研究
1
2021
... 为此,学者们对直驱风机并网诱发SSO问题进行了广泛的研究.文献[7 -8 ]针对风电机组的次同步振荡问题,从特性、分析方法和抑制措施等方面进行了综述.文献[9 -11 ]研究指出,直驱风电机组并入弱电网诱发SSO现象的主要因素之一是网侧变流器与电网之间的交互作用.文献[12 ]研究表明,直驱风机控制系统锁相环参数、电流内环参数对SSO有明显的影响.文献[13 ]用自抗扰控制(active disturbance rejection control,ADRC)替换电流内环PI控制器,并阐述ADRC抑制SSO原理,但其控制器参数整定过于繁琐.文献[14 ]建立直驱式风机并网变流器数学模型,用线性自抗扰控制(linear active disturbance rejection control,ADRC)替换电流内环PI控制器,简化了控制器参数整定的难度.文献[15 ]提出一阶LADRC电流内环控制器设计,可抵消线路中的次同步频率分量,虽能有效抑制SSO现象,但存在较大的误差与超调量.文献[16 ]提出基于一阶总扰动偏差控制的微分前馈LADRC,该控制器不仅可以减小跟踪误差且具有较强的抗干扰性能,但其不足之处在于功率波动范围较大.文献[17 ]在dq 坐标系下建立了网侧变流器的阻抗模型,并结合广义Nyquist判据对风电并网系统稳定性影响因素进行了分析.文献[18 ]分析了接入电网强度对并网系统稳定性的影响. ...
Research on double closed-loop control system of wind power grid-connected inverter
1
2021
... 为此,学者们对直驱风机并网诱发SSO问题进行了广泛的研究.文献[7 -8 ]针对风电机组的次同步振荡问题,从特性、分析方法和抑制措施等方面进行了综述.文献[9 -11 ]研究指出,直驱风电机组并入弱电网诱发SSO现象的主要因素之一是网侧变流器与电网之间的交互作用.文献[12 ]研究表明,直驱风机控制系统锁相环参数、电流内环参数对SSO有明显的影响.文献[13 ]用自抗扰控制(active disturbance rejection control,ADRC)替换电流内环PI控制器,并阐述ADRC抑制SSO原理,但其控制器参数整定过于繁琐.文献[14 ]建立直驱式风机并网变流器数学模型,用线性自抗扰控制(linear active disturbance rejection control,ADRC)替换电流内环PI控制器,简化了控制器参数整定的难度.文献[15 ]提出一阶LADRC电流内环控制器设计,可抵消线路中的次同步频率分量,虽能有效抑制SSO现象,但存在较大的误差与超调量.文献[16 ]提出基于一阶总扰动偏差控制的微分前馈LADRC,该控制器不仅可以减小跟踪误差且具有较强的抗干扰性能,但其不足之处在于功率波动范围较大.文献[17 ]在dq 坐标系下建立了网侧变流器的阻抗模型,并结合广义Nyquist判据对风电并网系统稳定性影响因素进行了分析.文献[18 ]分析了接入电网强度对并网系统稳定性的影响. ...
基于一阶LADRC控制的直驱风机次同步振荡抑制策略
1
2022
... 为此,学者们对直驱风机并网诱发SSO问题进行了广泛的研究.文献[7 -8 ]针对风电机组的次同步振荡问题,从特性、分析方法和抑制措施等方面进行了综述.文献[9 -11 ]研究指出,直驱风电机组并入弱电网诱发SSO现象的主要因素之一是网侧变流器与电网之间的交互作用.文献[12 ]研究表明,直驱风机控制系统锁相环参数、电流内环参数对SSO有明显的影响.文献[13 ]用自抗扰控制(active disturbance rejection control,ADRC)替换电流内环PI控制器,并阐述ADRC抑制SSO原理,但其控制器参数整定过于繁琐.文献[14 ]建立直驱式风机并网变流器数学模型,用线性自抗扰控制(linear active disturbance rejection control,ADRC)替换电流内环PI控制器,简化了控制器参数整定的难度.文献[15 ]提出一阶LADRC电流内环控制器设计,可抵消线路中的次同步频率分量,虽能有效抑制SSO现象,但存在较大的误差与超调量.文献[16 ]提出基于一阶总扰动偏差控制的微分前馈LADRC,该控制器不仅可以减小跟踪误差且具有较强的抗干扰性能,但其不足之处在于功率波动范围较大.文献[17 ]在dq 坐标系下建立了网侧变流器的阻抗模型,并结合广义Nyquist判据对风电并网系统稳定性影响因素进行了分析.文献[18 ]分析了接入电网强度对并网系统稳定性的影响. ...
Subsynchronous oscillation mitigation strategy based on first-order LADRC for direct-drive wind turbines
1
2022
... 为此,学者们对直驱风机并网诱发SSO问题进行了广泛的研究.文献[7 -8 ]针对风电机组的次同步振荡问题,从特性、分析方法和抑制措施等方面进行了综述.文献[9 -11 ]研究指出,直驱风电机组并入弱电网诱发SSO现象的主要因素之一是网侧变流器与电网之间的交互作用.文献[12 ]研究表明,直驱风机控制系统锁相环参数、电流内环参数对SSO有明显的影响.文献[13 ]用自抗扰控制(active disturbance rejection control,ADRC)替换电流内环PI控制器,并阐述ADRC抑制SSO原理,但其控制器参数整定过于繁琐.文献[14 ]建立直驱式风机并网变流器数学模型,用线性自抗扰控制(linear active disturbance rejection control,ADRC)替换电流内环PI控制器,简化了控制器参数整定的难度.文献[15 ]提出一阶LADRC电流内环控制器设计,可抵消线路中的次同步频率分量,虽能有效抑制SSO现象,但存在较大的误差与超调量.文献[16 ]提出基于一阶总扰动偏差控制的微分前馈LADRC,该控制器不仅可以减小跟踪误差且具有较强的抗干扰性能,但其不足之处在于功率波动范围较大.文献[17 ]在dq 坐标系下建立了网侧变流器的阻抗模型,并结合广义Nyquist判据对风电并网系统稳定性影响因素进行了分析.文献[18 ]分析了接入电网强度对并网系统稳定性的影响. ...
弱电网下改进LADRC抑制直驱风机次同步振荡研究
2
2023
... 为此,学者们对直驱风机并网诱发SSO问题进行了广泛的研究.文献[7 -8 ]针对风电机组的次同步振荡问题,从特性、分析方法和抑制措施等方面进行了综述.文献[9 -11 ]研究指出,直驱风电机组并入弱电网诱发SSO现象的主要因素之一是网侧变流器与电网之间的交互作用.文献[12 ]研究表明,直驱风机控制系统锁相环参数、电流内环参数对SSO有明显的影响.文献[13 ]用自抗扰控制(active disturbance rejection control,ADRC)替换电流内环PI控制器,并阐述ADRC抑制SSO原理,但其控制器参数整定过于繁琐.文献[14 ]建立直驱式风机并网变流器数学模型,用线性自抗扰控制(linear active disturbance rejection control,ADRC)替换电流内环PI控制器,简化了控制器参数整定的难度.文献[15 ]提出一阶LADRC电流内环控制器设计,可抵消线路中的次同步频率分量,虽能有效抑制SSO现象,但存在较大的误差与超调量.文献[16 ]提出基于一阶总扰动偏差控制的微分前馈LADRC,该控制器不仅可以减小跟踪误差且具有较强的抗干扰性能,但其不足之处在于功率波动范围较大.文献[17 ]在dq 坐标系下建立了网侧变流器的阻抗模型,并结合广义Nyquist判据对风电并网系统稳定性影响因素进行了分析.文献[18 ]分析了接入电网强度对并网系统稳定性的影响. ...
... 通过以上分析,结合文献[16 ]对输入信号进行一阶求导,从而提高系统响应速度、减小跟踪误差、缩小功率波动范围.故改进LADRC的数学模型为: ...
Inhibition of subsynchronous oscillation of direct-drive wind turbine by improved LADRC in weak grids
2
2023
... 为此,学者们对直驱风机并网诱发SSO问题进行了广泛的研究.文献[7 -8 ]针对风电机组的次同步振荡问题,从特性、分析方法和抑制措施等方面进行了综述.文献[9 -11 ]研究指出,直驱风电机组并入弱电网诱发SSO现象的主要因素之一是网侧变流器与电网之间的交互作用.文献[12 ]研究表明,直驱风机控制系统锁相环参数、电流内环参数对SSO有明显的影响.文献[13 ]用自抗扰控制(active disturbance rejection control,ADRC)替换电流内环PI控制器,并阐述ADRC抑制SSO原理,但其控制器参数整定过于繁琐.文献[14 ]建立直驱式风机并网变流器数学模型,用线性自抗扰控制(linear active disturbance rejection control,ADRC)替换电流内环PI控制器,简化了控制器参数整定的难度.文献[15 ]提出一阶LADRC电流内环控制器设计,可抵消线路中的次同步频率分量,虽能有效抑制SSO现象,但存在较大的误差与超调量.文献[16 ]提出基于一阶总扰动偏差控制的微分前馈LADRC,该控制器不仅可以减小跟踪误差且具有较强的抗干扰性能,但其不足之处在于功率波动范围较大.文献[17 ]在dq 坐标系下建立了网侧变流器的阻抗模型,并结合广义Nyquist判据对风电并网系统稳定性影响因素进行了分析.文献[18 ]分析了接入电网强度对并网系统稳定性的影响. ...
... 通过以上分析,结合文献[16 ]对输入信号进行一阶求导,从而提高系统响应速度、减小跟踪误差、缩小功率波动范围.故改进LADRC的数学模型为: ...
考虑频率耦合特性的并网逆变器阻抗特性与稳定性研究
3
2021
... 为此,学者们对直驱风机并网诱发SSO问题进行了广泛的研究.文献[7 -8 ]针对风电机组的次同步振荡问题,从特性、分析方法和抑制措施等方面进行了综述.文献[9 -11 ]研究指出,直驱风电机组并入弱电网诱发SSO现象的主要因素之一是网侧变流器与电网之间的交互作用.文献[12 ]研究表明,直驱风机控制系统锁相环参数、电流内环参数对SSO有明显的影响.文献[13 ]用自抗扰控制(active disturbance rejection control,ADRC)替换电流内环PI控制器,并阐述ADRC抑制SSO原理,但其控制器参数整定过于繁琐.文献[14 ]建立直驱式风机并网变流器数学模型,用线性自抗扰控制(linear active disturbance rejection control,ADRC)替换电流内环PI控制器,简化了控制器参数整定的难度.文献[15 ]提出一阶LADRC电流内环控制器设计,可抵消线路中的次同步频率分量,虽能有效抑制SSO现象,但存在较大的误差与超调量.文献[16 ]提出基于一阶总扰动偏差控制的微分前馈LADRC,该控制器不仅可以减小跟踪误差且具有较强的抗干扰性能,但其不足之处在于功率波动范围较大.文献[17 ]在dq 坐标系下建立了网侧变流器的阻抗模型,并结合广义Nyquist判据对风电并网系统稳定性影响因素进行了分析.文献[18 ]分析了接入电网强度对并网系统稳定性的影响. ...
... 根据文献[17 ]可知,若阻抗比环路增益矩阵的2条特征值曲线满足Nyquist判据时,则系统是稳定的.阻抗比特征值l 1 、 l 2
... 分别取线路阻抗3、1.95 mH(对应SCR分别为1.9、2.9),代入式(25) ,分析不同控制方法下线路阻抗值对网侧变换器并网系统稳定性的影响[17 -18 ,24 ] .图7 为传统LADRC阻抗伯德图,可见,当处于弱电网时,线路阻抗与网侧变换器阻抗幅值无交点,表明在该工况下采用传统LADRC控制策略时并网系统稳定运行;但处于极弱电网工况时,线路阻抗与网侧变换器阻抗幅值在30.9 Hz与68.9 Hz处均有交点,对应的相频特性位于负阻尼区,表明网侧变换器并网系统在该工况下采用传统LADRC控制策略存在次/超同步振荡风险.图8 为改进LADRC阻抗伯德图,可以发现,当处于极弱电网与弱电网工况时,线路阻抗与网侧变换器阻抗幅值无交点,表明在采用改进LADRC控制策略时并网系统稳定运行. ...
Study on impedance characteristics and stability of grid-connected inverter considering frequency coupling characteristics
3
2021
... 为此,学者们对直驱风机并网诱发SSO问题进行了广泛的研究.文献[7 -8 ]针对风电机组的次同步振荡问题,从特性、分析方法和抑制措施等方面进行了综述.文献[9 -11 ]研究指出,直驱风电机组并入弱电网诱发SSO现象的主要因素之一是网侧变流器与电网之间的交互作用.文献[12 ]研究表明,直驱风机控制系统锁相环参数、电流内环参数对SSO有明显的影响.文献[13 ]用自抗扰控制(active disturbance rejection control,ADRC)替换电流内环PI控制器,并阐述ADRC抑制SSO原理,但其控制器参数整定过于繁琐.文献[14 ]建立直驱式风机并网变流器数学模型,用线性自抗扰控制(linear active disturbance rejection control,ADRC)替换电流内环PI控制器,简化了控制器参数整定的难度.文献[15 ]提出一阶LADRC电流内环控制器设计,可抵消线路中的次同步频率分量,虽能有效抑制SSO现象,但存在较大的误差与超调量.文献[16 ]提出基于一阶总扰动偏差控制的微分前馈LADRC,该控制器不仅可以减小跟踪误差且具有较强的抗干扰性能,但其不足之处在于功率波动范围较大.文献[17 ]在dq 坐标系下建立了网侧变流器的阻抗模型,并结合广义Nyquist判据对风电并网系统稳定性影响因素进行了分析.文献[18 ]分析了接入电网强度对并网系统稳定性的影响. ...
... 根据文献[17 ]可知,若阻抗比环路增益矩阵的2条特征值曲线满足Nyquist判据时,则系统是稳定的.阻抗比特征值l 1 、 l 2
... 分别取线路阻抗3、1.95 mH(对应SCR分别为1.9、2.9),代入式(25) ,分析不同控制方法下线路阻抗值对网侧变换器并网系统稳定性的影响[17 -18 ,24 ] .图7 为传统LADRC阻抗伯德图,可见,当处于弱电网时,线路阻抗与网侧变换器阻抗幅值无交点,表明在该工况下采用传统LADRC控制策略时并网系统稳定运行;但处于极弱电网工况时,线路阻抗与网侧变换器阻抗幅值在30.9 Hz与68.9 Hz处均有交点,对应的相频特性位于负阻尼区,表明网侧变换器并网系统在该工况下采用传统LADRC控制策略存在次/超同步振荡风险.图8 为改进LADRC阻抗伯德图,可以发现,当处于极弱电网与弱电网工况时,线路阻抗与网侧变换器阻抗幅值无交点,表明在采用改进LADRC控制策略时并网系统稳定运行. ...
自抗扰并网逆变器宽频带阻抗建模与稳定性对比分析研究
3
2020
... 为此,学者们对直驱风机并网诱发SSO问题进行了广泛的研究.文献[7 -8 ]针对风电机组的次同步振荡问题,从特性、分析方法和抑制措施等方面进行了综述.文献[9 -11 ]研究指出,直驱风电机组并入弱电网诱发SSO现象的主要因素之一是网侧变流器与电网之间的交互作用.文献[12 ]研究表明,直驱风机控制系统锁相环参数、电流内环参数对SSO有明显的影响.文献[13 ]用自抗扰控制(active disturbance rejection control,ADRC)替换电流内环PI控制器,并阐述ADRC抑制SSO原理,但其控制器参数整定过于繁琐.文献[14 ]建立直驱式风机并网变流器数学模型,用线性自抗扰控制(linear active disturbance rejection control,ADRC)替换电流内环PI控制器,简化了控制器参数整定的难度.文献[15 ]提出一阶LADRC电流内环控制器设计,可抵消线路中的次同步频率分量,虽能有效抑制SSO现象,但存在较大的误差与超调量.文献[16 ]提出基于一阶总扰动偏差控制的微分前馈LADRC,该控制器不仅可以减小跟踪误差且具有较强的抗干扰性能,但其不足之处在于功率波动范围较大.文献[17 ]在dq 坐标系下建立了网侧变流器的阻抗模型,并结合广义Nyquist判据对风电并网系统稳定性影响因素进行了分析.文献[18 ]分析了接入电网强度对并网系统稳定性的影响. ...
... 分别取线路阻抗3、1.95 mH(对应SCR分别为1.9、2.9),代入式(25) ,分析不同控制方法下线路阻抗值对网侧变换器并网系统稳定性的影响[17 -18 ,24 ] .图7 为传统LADRC阻抗伯德图,可见,当处于弱电网时,线路阻抗与网侧变换器阻抗幅值无交点,表明在该工况下采用传统LADRC控制策略时并网系统稳定运行;但处于极弱电网工况时,线路阻抗与网侧变换器阻抗幅值在30.9 Hz与68.9 Hz处均有交点,对应的相频特性位于负阻尼区,表明网侧变换器并网系统在该工况下采用传统LADRC控制策略存在次/超同步振荡风险.图8 为改进LADRC阻抗伯德图,可以发现,当处于极弱电网与弱电网工况时,线路阻抗与网侧变换器阻抗幅值无交点,表明在采用改进LADRC控制策略时并网系统稳定运行. ...
... 文献[12 ,18 ]揭示了PI控制器参数对直驱风机SSO影响较为明显,为了验证前文所提出改进LADRC电流内环控制器,在PSCAD/EMTDC中建立如图1 所示的等值仿真模型进行验证,将3种不同的控制策略进行对比.其仿真模型参数如表2 所示. ...
Broadband impedance modeling and stability comparative analysis of ADRC grid-connected inverter
3
2020
... 为此,学者们对直驱风机并网诱发SSO问题进行了广泛的研究.文献[7 -8 ]针对风电机组的次同步振荡问题,从特性、分析方法和抑制措施等方面进行了综述.文献[9 -11 ]研究指出,直驱风电机组并入弱电网诱发SSO现象的主要因素之一是网侧变流器与电网之间的交互作用.文献[12 ]研究表明,直驱风机控制系统锁相环参数、电流内环参数对SSO有明显的影响.文献[13 ]用自抗扰控制(active disturbance rejection control,ADRC)替换电流内环PI控制器,并阐述ADRC抑制SSO原理,但其控制器参数整定过于繁琐.文献[14 ]建立直驱式风机并网变流器数学模型,用线性自抗扰控制(linear active disturbance rejection control,ADRC)替换电流内环PI控制器,简化了控制器参数整定的难度.文献[15 ]提出一阶LADRC电流内环控制器设计,可抵消线路中的次同步频率分量,虽能有效抑制SSO现象,但存在较大的误差与超调量.文献[16 ]提出基于一阶总扰动偏差控制的微分前馈LADRC,该控制器不仅可以减小跟踪误差且具有较强的抗干扰性能,但其不足之处在于功率波动范围较大.文献[17 ]在dq 坐标系下建立了网侧变流器的阻抗模型,并结合广义Nyquist判据对风电并网系统稳定性影响因素进行了分析.文献[18 ]分析了接入电网强度对并网系统稳定性的影响. ...
... 分别取线路阻抗3、1.95 mH(对应SCR分别为1.9、2.9),代入式(25) ,分析不同控制方法下线路阻抗值对网侧变换器并网系统稳定性的影响[17 -18 ,24 ] .图7 为传统LADRC阻抗伯德图,可见,当处于弱电网时,线路阻抗与网侧变换器阻抗幅值无交点,表明在该工况下采用传统LADRC控制策略时并网系统稳定运行;但处于极弱电网工况时,线路阻抗与网侧变换器阻抗幅值在30.9 Hz与68.9 Hz处均有交点,对应的相频特性位于负阻尼区,表明网侧变换器并网系统在该工况下采用传统LADRC控制策略存在次/超同步振荡风险.图8 为改进LADRC阻抗伯德图,可以发现,当处于极弱电网与弱电网工况时,线路阻抗与网侧变换器阻抗幅值无交点,表明在采用改进LADRC控制策略时并网系统稳定运行. ...
... 文献[12 ,18 ]揭示了PI控制器参数对直驱风机SSO影响较为明显,为了验证前文所提出改进LADRC电流内环控制器,在PSCAD/EMTDC中建立如图1 所示的等值仿真模型进行验证,将3种不同的控制策略进行对比.其仿真模型参数如表2 所示. ...
1
2008
... 本文将结合传统LADRC和一次微分前馈项环节,继续改进LSEF来补偿扰动项,减小跟踪误差及扰动项对并网系统稳定性的影响.由于线性微分跟踪器会在系统进入稳态后引起高频颤振[19 ] ,因此本文只考虑LADRC由线性扩张状态观察器(linear extended state observer,LESO)与LSEF构成的LADRC. ...
1
2008
... 本文将结合传统LADRC和一次微分前馈项环节,继续改进LSEF来补偿扰动项,减小跟踪误差及扰动项对并网系统稳定性的影响.由于线性微分跟踪器会在系统进入稳态后引起高频颤振[19 ] ,因此本文只考虑LADRC由线性扩张状态观察器(linear extended state observer,LESO)与LSEF构成的LADRC. ...
ADRC-based current control for grid-tied inverters:design,analysis,and verification
1
2019
... 根据跟踪误差的定义[20 ] 得出跟踪误差为 ...
新型电力系统背景下新能源送出合理消纳率研究
1
2023
... 风电基本与负荷中心呈逆向分布,因此风电的大规模利用与消纳需要进行长距离输送[21 ] ,而风电场与大型电网之间的线路阻抗已成为影响SSO的主要因素,故研究线路阻抗值对并网系统稳定性尤为重要. ...
Research on reasonable consumption rate of new energy transmission under the new power system
1
2023
... 风电基本与负荷中心呈逆向分布,因此风电的大规模利用与消纳需要进行长距离输送[21 ] ,而风电场与大型电网之间的线路阻抗已成为影响SSO的主要因素,故研究线路阻抗值对并网系统稳定性尤为重要. ...
Sequence impedance modeling and converter-grid resonance analysis considering DC bus dynamics and mirrored harmonics
2
2018
... 仅考虑扰动项时,取相同的ω 0 、 ω c [22 ] 如图3 所示. ...
... 根据文献[22 -23 ]得到弱电网情况下线路阻抗和各个控制环节,且能够反应SSO现象的等效阻抗模型为 ...
直驱风电场接入弱电网宽频带振荡机理与抑制方法(一):宽频带阻抗特性与振荡机理分析
1
2019
... 根据文献[22 -23 ]得到弱电网情况下线路阻抗和各个控制环节,且能够反应SSO现象的等效阻抗模型为 ...
Mechanism analysis and suppression method of wideband oscillation of PMSG wind farms connected to weak grid (part Ⅰ):analysis of wideband impedance characteristics and oscillation mechanism
1
2019
... 根据文献[22 -23 ]得到弱电网情况下线路阻抗和各个控制环节,且能够反应SSO现象的等效阻抗模型为 ...
电压型虚拟同步发电机控制策略下的双馈风电机组阻抗及次同步振荡特性
2
2019
... 为验证上述阻抗模型的正确性,根据考虑频率耦合效应时的正序导纳的数学模型[24 ] 和表1 参数,在仿真软件进行扫频,得到导纳模型线路.阻抗分别取3、2.3、1.95 mH(对应SCR分别为1.9、2.5、2.9). ...
... 分别取线路阻抗3、1.95 mH(对应SCR分别为1.9、2.9),代入式(25) ,分析不同控制方法下线路阻抗值对网侧变换器并网系统稳定性的影响[17 -18 ,24 ] .图7 为传统LADRC阻抗伯德图,可见,当处于弱电网时,线路阻抗与网侧变换器阻抗幅值无交点,表明在该工况下采用传统LADRC控制策略时并网系统稳定运行;但处于极弱电网工况时,线路阻抗与网侧变换器阻抗幅值在30.9 Hz与68.9 Hz处均有交点,对应的相频特性位于负阻尼区,表明网侧变换器并网系统在该工况下采用传统LADRC控制策略存在次/超同步振荡风险.图8 为改进LADRC阻抗伯德图,可以发现,当处于极弱电网与弱电网工况时,线路阻抗与网侧变换器阻抗幅值无交点,表明在采用改进LADRC控制策略时并网系统稳定运行. ...
Impedance and sub-synchronous oscillation characteristics of doubly-fed induction generators with control strategy of voltage virtual synchronous generator
2
2019
... 为验证上述阻抗模型的正确性,根据考虑频率耦合效应时的正序导纳的数学模型[24 ] 和表1 参数,在仿真软件进行扫频,得到导纳模型线路.阻抗分别取3、2.3、1.95 mH(对应SCR分别为1.9、2.5、2.9). ...
... 分别取线路阻抗3、1.95 mH(对应SCR分别为1.9、2.9),代入式(25) ,分析不同控制方法下线路阻抗值对网侧变换器并网系统稳定性的影响[17 -18 ,24 ] .图7 为传统LADRC阻抗伯德图,可见,当处于弱电网时,线路阻抗与网侧变换器阻抗幅值无交点,表明在该工况下采用传统LADRC控制策略时并网系统稳定运行;但处于极弱电网工况时,线路阻抗与网侧变换器阻抗幅值在30.9 Hz与68.9 Hz处均有交点,对应的相频特性位于负阻尼区,表明网侧变换器并网系统在该工况下采用传统LADRC控制策略存在次/超同步振荡风险.图8 为改进LADRC阻抗伯德图,可以发现,当处于极弱电网与弱电网工况时,线路阻抗与网侧变换器阻抗幅值无交点,表明在采用改进LADRC控制策略时并网系统稳定运行. ...
1
1997
... 交流电网强度越小,SSO越剧烈[12 ] .文献[25 ]提出电网强度用短路电流比来描述,定义短路电流比≤3的电网为弱电网,短路电流比<2的电网为极弱电网,设置不同的SCR进行仿真分析. ...
大规模双馈风电场次同步谐振的分析与抑制
1
2014
... 低风速情况下SSO易发生的概率较大,风速越低,系统稳定性越差[26 ] .结合实际工况,设置SCR为2.5,通过调节等效电流源电流的大小来设置不同的风速进行仿真分析. ...
Analysis and mitigation of SSR problems in large-scale wind farms with doubly-fed wind turbines
1
2014
... 低风速情况下SSO易发生的概率较大,风速越低,系统稳定性越差[26 ] .结合实际工况,设置SCR为2.5,通过调节等效电流源电流的大小来设置不同的风速进行仿真分析. ...