基于多特征提取-卷积神经网络-长短期记忆网络的短期风电功率预测方法

doi:10.12096/j.2096-4528.pgt.23101

基于多特征提取-卷积神经网络-长短期记忆网络的短期风电功率预测方法

匡洪海, 郭茜

湖南工业大学电气与信息工程学院，湖南省株洲市 412007

Short-Term Wind Power Prediction Method Based on Multimodal Feature Extraction-Convolutional Neural Network-Long-Short Term Memory Network

KUANG Honghai, GUO Qian

College of Electrical and Information Engineering, Hunan University of Technology, Zhuzhou 412007, Hunan Province, China

收稿日期: 2023-08-25 修回日期: 2023-12-18

基金资助:

国家自然科学基金项目. 51977072

Received: 2023-08-25 Revised: 2023-12-18

作者简介 About authors

匡洪海(1972)，女，博士，教授，研究方向为新能源发电与并网，khhzyz@163.com；

郭茜(1996)，女，硕士研究生，研究方向为风电功率预测，12458044@qq.com。

摘要

目的天气和随机因素会改变误差的统计特征，因此考虑对影响风电功率的多种气候因素进行特征提取，为优化功率时序特征提取，提出基于多特征提取(multimodal feature extraction，MFE)-卷积神经网络(convolutional neural network，CNN)-长短期记忆(long-short term memory，LSTM)网络的风电功率预测方法。方法首先，对数值天气预报(numerical weather prediction，NWP)数据提取11种统计性特征，通过提取基本特征和统计性特征对原始数据进行聚类，并根据类别分别建立预测模型，以提高预测模型的适应性；其次，在网络架构上对LSTM进行改进，通过CNN的特征提取能力和LSTM的非线性序列预测能力，实现对风电功率历史信息和NWP数据的充分挖掘。最后，利用我国新疆某风电场数据，通过MFE消融实验、CNN消融实验，验证了所提短期风电功率预测方法的有效性和优越性。结果相比于自回归移动平均(autoregressive integrated moving average，ARIMA)、全连接循环神经网络(fully recurrent neural network，FRNN)模型和MFE-LSTM、CNN-LSTM模型，MFE-CNN-LSTM预测方法的均方根误差与平均绝对误差均有所下降。结论 MFE-CNN-LSTM预测方法可有效提取特征，并且MFE与CNN有效提升了预测准确性。

关键词： 多特征提取 ; 卷积神经网络 ; 长短期记忆网络 ; k-均值聚类算法 ; 风电功率预测 ; 短期预测 ; 消融实验

Abstract

Objectives Weather and random factors can alter the statistical characteristics of errors. Therefore, this study considers feature extraction of various climate factors that affect wind power. To optimize the extraction of power time series features, a wind power prediction method based on multi-feature extraction (MFE), convolutional neural network (CNN), and long short-term memory (LSTM) network is proposed. Methods Firstly, 11 statistical features are extracted from numerical weather prediction (NWP) data. By extracting basic and statistical features, the original data is clustered, and prediction models are established according to categories to improve the adaptability of prediction models. Next, the network architecture of LSTM is improved. By leveraging the feature extraction ability of CNN and the nonlinear sequence prediction ability of LSTM, the historical information of wind power and NWP data is thoroughly explored. Finally, using the data from a wind farm in Xinjiang, China, the effectiveness and advantages of the proposed short-term wind power prediction method are verified by MFE and CNN ablation experiments. Results The MFE-CNN-LSTM prediction method shows a decrease in both root mean square error and mean absolute error, compared with the autoregressive integrated moving average (ARIMA), fully recurrent neural network (FRNN), MFE-LSTM and CNN-LSTM models. Conclusions The MFE-CNN-LSTM prediction method can effectively extract features, and MFE and CNN effectively improve prediction accuracy.

Keywords： multi-feature extraction ; convolutional neural network ; long short-term memory networks ; k-means clustering algorithm ; wind power prediction ; short-term prediction ; ablation experiment

PDF (2830KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

匡洪海, 郭茜. 基于多特征提取-卷积神经网络-长短期记忆网络的短期风电功率预测方法. 发电技术[J], 2025, 46(1): 93-102 DOI:10.12096/j.2096-4528.pgt.23101

KUANG Honghai, GUO Qian. Short-Term Wind Power Prediction Method Based on Multimodal Feature Extraction-Convolutional Neural Network-Long-Short Term Memory Network. Power Generation Technology[J], 2025, 46(1): 93-102 DOI:10.12096/j.2096-4528.pgt.23101

0 引言

风电功率预测情况会影响风电场的发电调度计划，且风电功率的波动性会限制其调频能力，若仅依据日前调度计划进行调度会出现电力系统功率不平衡、日前调度计划不合理等问题^[1-2]。风电功率预测误差与储能容量有很强的关联性^[3]，若无法准确预测风电功率，为保证运行安全，电网需要更多备用容量平衡波动^[4]，因此提升短期风电功率预测的精确性对风电调度至关重要^[5-10]。

几乎所有数据驱动型预测模型预测效果都会受到原始数据质量优劣的制约。风电功率预测方法主要涉及的数据包括风电场站基础数据、环境数据、气象监测数据和数值天气预测(numerical weather prediction，NWP)数据等。对于物理法，风电场站的地形数据、地表覆盖情况和杂物遮挡情况是影响模型建立的重要数据；对于统计法，普遍采用历史风电功率数据和NWP数据作为输入。风电功率具有强非线性、随机性，且存在限电的情况，这些特点使得风电功率的波动性规律较模糊，需要进行预处理，减少异常数据对模型训练过程的干扰。NWP提供的数据则需要判断其可靠性，气象监测数据对NWP系统而言是重要的修正依据^[11-13]。

卷积神经网络(convolutional neural network，CNN)^[14]是第一批可以用反向传播有效训练的深度学习网络，也是专门处理类网格数据的神经网络，包括时间序列(一维网格)和图像(二维网格)。CNN具有稀疏交互、参数共享和等变表示的特点，能有效降低训练需要的存储空间、减少计算量、提高统计效率^[15-16]。CNN采用卷积运算特异化神经网络，能有效处理网格数据结构，尤其是二维数据，相比而言，一维数据的处理效果较弱。

长短期记忆(long-short term memory，LSTM)神经网络^[17-18]是由若干记忆单元构成的。LSTM包含输入门、输出门和遗忘门。这3个门之间的交互操作使得LSTM有足够的能力解决一般网络无法学习的长期依赖性问题。LSTM是全连接循环神经网络(fully recurrent neural network，FRNN)的衍变形态，是在循环神经网络(recurrent neural network，RNN)的基础上引入了门控，使单元环节的输入受到限制，该架构显著改善了梯度消失及爆炸的问题^[19-20]。

综上，本文提出基于多特征提取(multimodal feature extraction，MFE)-CNN-LSTM的风电功率预测模型。为解决LSTM预测模型的滞后问题，采用结合CNN网络提取时序特征，并对输入数据进行设计；为解决CNN网络的过拟合问题，采用批标准化层和提前终止训练的解决方案，并采用缩放指数线性单元(scaled exponential linear unit，SELU)激活函数避免可能出现的梯度消失问题；由于天气和随机因素可能会改变误差的统计特征，为此对影响风电功率的多种天气因素进行特征提取，通过NWP数据的多特征提取达到精准预测的目的。

1 特征提取

由于风电功率受到众多因素的影响，因此将训练集根据NWP基本特征和统计特征聚类，为每个聚类结果建立对应的预测模型。

本文所用数据来自我国新疆某风电场2016年的历史数据。风电场装机容量为50 MW，历史数据的分辨率为15 min，包含风力发电机的历史风速、风向、实际发电量。NWP数据包含10、30、50、70 m高度的历史风速和风向，以及温度、湿度、气压数据，共11个变量，每个变量每天有96个数据，预报时间间隔为15 min。

原始样本数据集分成训练集与测试集，训练集用于训练模型，测试集用于检测预测结果。将训练集中的一部分作为验证集，训练集其余部分训练完模型后，用验证集验证模型的好坏，以辅助模型调整超参数，其中训练集占比80%，验证集占比10%，测试集占比10%。为消除输入变量之间量纲的差别，对所有变量进行归一化，其中风向取角度的余弦值与正弦值^[21]，其他变量采用最大值-最小值归一化方法。通过对数据进行归一化处理，提取了基本特征和统计性特征共184个，并对此聚类得到3类数据，表1总结了所有归一化后的变量。根据每一日的15个NWP变量提取出19个基本特征和165个统计特征，一天的特征组成一个165维向量。

表1 归一化变量

Tab. 1 Normalized variables

类型	参数	意义
输入变量	V_{i b}	第i天高度b m处的风速(b=10, 30, 50, 70)
	D_{i b,1}	第i天高度b m处的风向角度的正弦值(b=10, 30, 50, 70)
	D_{i b,2}	第i天高度b m处的风向角度的余弦值(b=10, 30, 50, 70)
	Tⁱ	第i天的温度
	Sⁱ	第i天的湿度
	Hⁱ	第i天的压力
输出变量	Pⁱ	第i天的风电功率

新窗口打开| 下载CSV

由于高维模型设计的困难，采用t-分布邻域嵌入(t-distributed stochastic neighbor embedding，t-SNE)法使特征向量降维到二维平面。降维后再用k-均值算法聚类。以特征数据作为输入，对不同聚类簇建立CNN-LSTM模型。预测特定一天的风电功率时，NWP的数据可以确定那一天属于的聚类簇，并采用对应的CNN-LSTM模型进行预测。每一组NWP数据的处理方式保持一致，具体特征提取的方法如下。

首先进行基本特征提取，在184个特征中，有19个特征由15个NWP变量直接得到，如表2所示。另外165个特征由15个NWP变量的对应统计量算式得到。

表2 基本特征变量

Tab. 2 Basic characteristic variables

变量	意义
$v_{b, 1}^{i}$	第i天高度b m处的最小风速(b=10, 30, 50, 70)
$v_{b, 2}^{i}$	第i天高度b m处的最大风速(b=10, 30, 50, 70)
${\bar{d}}_{b, 1}^{i}$	第i天高度b m处的风向角度的正弦值的平均值(b =10, 30,50, 70)
${\bar{d}}_{b, 2}^{i}$	第i天高度b m处的风向角度的余弦值的平均值(b =10, 30,50, 70)
$\bar{t}$ ⁱ	第i天温度的平均值
$\bar{s}$ ⁱ	第i天湿度的平均值
$\bar{h}$ ⁱ	第i天压力的平均值

新窗口打开| 下载CSV

为了聚类的有效性，从15个NWP变量中提取统计学特征，包括趋势因素Kⁱ_j 、序列相关性Cⁱ_j 、序列非相关性Gⁱ_j 、偏度Uⁱ_j 、峰度Fⁱ_j 、长期依赖性Oⁱ_j 和混沌性Zⁱ_j，j=1,…,15，它们的计算公式见文献[21-23]。

每个特征的取值范围不同，需要对统计特征进行logistic变换，确保每个特征变量的取值范围为[0, 1]。每天的多元NWP序列中可以提取165个统计学特征 $χ_{j}^{i}$ 和19个基本特征 $γ_{j}^{i}$ 。

χ_{j}^{i} = (K_{j}^{i}, C_{j}^{i, 1}, C_{j}^{i, 2}, G_{j}^{i, 1}, G_{j}^{i, 2}, U_{j}^{i, 1}, U_{j}^{i, 2}, F_{j}^{i, 1}, F_{j}^{i, 2}, Q_{j}^{i}, Z_{j}^{i})

(1)

γ_{j}^{i} = (v_{b, 1}^{i}, v_{b, 2}^{i}, {\bar{d}}_{b, 1}^{i}, {\bar{d}}_{b, 2}^{i}, {\bar{t}}^{i}, {\bar{s}}^{i}, {\bar{h}}^{i})

(2)

所有的184个特征可以集合成一个向量表达式：

Φ^{i} = (χ_{j}^{i}, γ_{j}^{i})

(3)

式中j=1,…,15。

特征向量是从NWP数据中提取的184个特征。高维特征的变化模式的复杂性不利于对预测模型的学习，因此考虑先通过聚类对数据进行分类，对各聚类类型的数据分别训练预测模型，在保留多维特征的基础上保证预测的准确性。为了聚类的便利性，先进行降维处理。

t-SNE降维方法^[24]能够提取大部分高维数据的局部结构，此外还能表现全局结构，包括在几个维度上存在的簇，因此被用于降维和高维特征可视化。通过t-SNE将每天的特征降维到二维量，方便实现聚类。t-SNE将高维点之间的欧氏距离特征变换成条件概率以表达数据点之间的相似性。

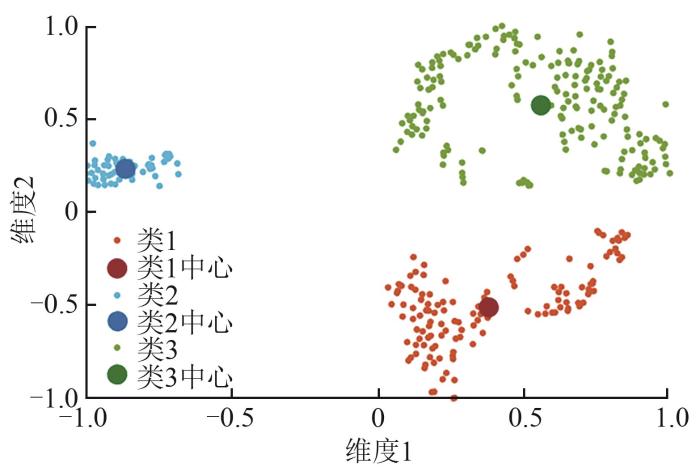
聚类可以在没有先验知识的条件时，根据数据之间的距离，将数据集划分为几组。根据数值天气状况对训练集聚类，对每个聚类建立独立的模型。k-均值算法的核心目标是将给定的数据集划分成k个簇(k是超参数)，并给出每个样本数据对应的中心点。本文采用k-均值算法对每日的特征向量进行聚类，聚类簇的数量k由肘部法确定为3。降维后的特征聚类结果如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 特征聚类结果

Fig. 1 Feature clustering results

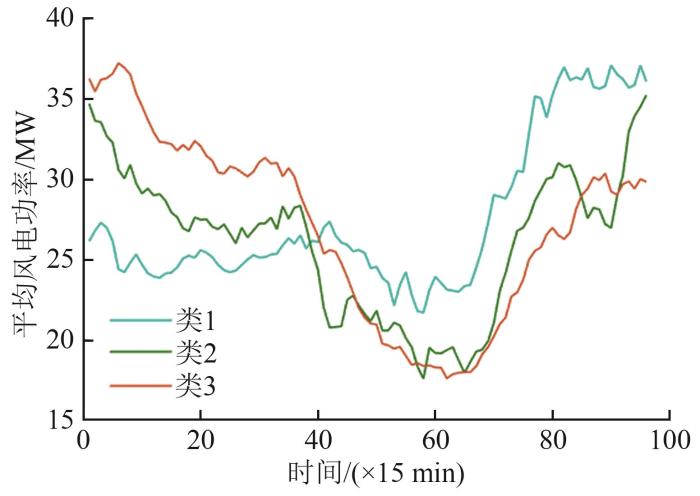
将属于3种类别的每日风电功率数据分别取平均值，得到的曲线如图2所示。可以看出，3种类别的功率平均值有不同的变化模式。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 3类功率的平均值曲线

Fig. 2 Average value curves of three power types

利用归一化的数据来计算变量间的Pearson相关系数(Pearson correlation coefficien，PCC)，根据PCC相关性分析推断，聚类分为3类的原因可能是：春季功率与风速、风向的正弦值、风向的余弦值、气压和相对湿度相关性更强；冬季功率与风速、气压相关性最强；夏季和秋季的功率受到气象因素影响的要素相似，都是风速、风向的正弦值、空气温度和相对湿度这些要素。

将184维特征值降维后再聚类得到3类数据，属于3种类别的数据可以分别作为3个模型的输入，通过不同类别的数据模型进行预测。

2 基于CNN-LSTM的时序特征提取模型

2.1 数据标准化

CNN中的全连接层对所有数据进行线性汇总运算，卷积层对局部数据进行非线性汇总运算。CNN和多层感知器的不同之处在于CNN使用了权重共享的概念，由卷积层实现。

在深度神经网络的训练期间，若数据没有标准化，可能使每个更新都对隐藏层的数值产生极端影响，低层权重符号的翻转可能导致中间状态与输出关系的反转，低层权重为0会导致输出退化问题。此外，如果神经元的输出值远超激活函数本身的定义域，也可能导致输出不正常。批标准化(batch normalization，BN)^[25]适用于网络任一输入层和隐藏层，减少多层分布的协调更新问题，使模型更易学习。

设需要标准化的是 H，即某层的小批量激活函数组成的矩阵，标准化形式为

H^{'} = \frac{H - μ}{σ}

(4)

式中： $μ$ 是每个单元均值组成的向量； $σ$ 是每个单元标准差组成的向量。对 H 矩阵逐行运算，每个元素H_ij 替换为 $(H_{i j} - μ_{j}) / σ_{j}$ 。

因此采用批标准化保持多层网络之中的输入分布基本不变，防止深层数据分布偏移导致的收敛困难，BN的方程如下：

μ_{B} = \frac{1}{κ} \sum_{i = 1}^{κ} x_{i}

(5)

σ_{B}^{2} = \frac{1}{κ} \sum_{i = 1}^{κ} (x_{i} - μ_{B})^{2}

(6)

{\hat{x}}_{i} = \frac{x_{i} - μ_{B}}{\sqrt[]{σ_{B}^{2} + ς}}

(7)

y_{i} = ρ {\hat{x}}_{i} + β \equiv {B_{N}}_{ρ, β} (x_{i})

(8)

式中：x_i 是某个mini-batch的第i个输入；y_i 是BN的输出；κ是mini-batch的输入总数；μ_B和σ $_{B}^{2}$ 分别是同一mini-batch的输入平均值和方差；ς是常量；ρ和β是训练得到的。经过BN处理可防止过拟合并提高训练速度。

与ReLU相比，激活函数中SELU具有更好的收敛性，可避免训练间梯度消失的问题^[26]。ReLU和SELU激活函数分别表示如下：

R_{e L U} (x) = m a x (0, x)

(9)

S_{E L U} (x) = \{\begin{matrix} λ x, & x > 0 \\ λ τ (e^{x} - 1), & x \leq 0 \end{matrix}

(10)

式中：λ=1.05；τ=1.67。

2.2 CNN特征提取的网络设计

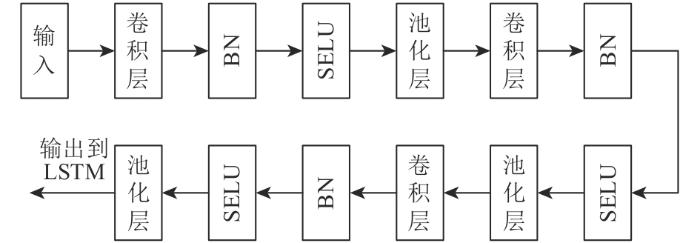
CNN网络部分作为风电功率特征提取的功能部分，其网络设计如图3所示，具体各层设计如下：

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 CNN网络设计

Fig. 3 CNN network design

1）卷积层。作为提取特征的关键层在网络中设置为3层卷积层，卷积层可以加强某一特征以实现特征提取，同时排除干扰因素、降低噪声影响。卷积层和池化层交替可以在特征不变的前提下减少维度空间和计算时间。3层卷积层中，第1个取192个卷积核，卷积核尺寸为3；第2个取128个卷积核，卷积核尺寸为3；第3个取64个卷积核，卷积核尺寸为3。

2）BN层。为了防止网络深层数据偏移，在每层卷积层后设置BN层，通过归一化对网络中间状态进行分布的重分配，平滑梯度函数，降低了对初始化值的依赖性，提高模型泛化能力和鲁棒性。

3）SELU。卷积层采用SELU激活函数，可在CNN部分避免梯度消失问题。

4）池化层。池化层也称子采样层，方法包括随机池化、空间金字塔池化等。本文采用最大池化，它用于提取局部最大值，相比绝对位置更强调相对位置特征，降低参数矩阵尺寸，防止过拟合。参数中池化窗口大小取2，stride取1，padding取valid。

从时间维度来说，NWP数据是时刻变化的，存在统计性规律，不同类型的气象因素变化的模式也有差异。CNN网络的数据输入设计如下：

1）将归一化后的风电功率和6个NWP数据(见表1)，以及提取的165个统计性特征值，总共172个特征值一起作为1D卷积神经网络的输入，具体包括功率，70 m高度的风速、70 m高度的风向角度的正弦值、余弦值，温度、湿度、气压，以及所有NWP归一化数据的趋势因素、序列相关性、序列非线性、偏度、峰度、长期依赖性、混沌性特征值，共计165个统计性特征值。

2）输入1D卷积神经网络的数据时间范围为1周(96×7=672个时刻点)，从需要预测的当天之前取1周的数据，即672×172的输入维度。

2.3 LSTM特征提取的网络设计

LSTM网络是克服FRNN梯度爆炸和梯度消失问题的一种变体，由于其独特的结构而非常擅长处理时间序列预测^[27]。

LSTM中记忆单元的门设计控制了信息传输的程度，可以有效解决反向传播中梯度消失的问题，门的实现通过激活函数完成，遗忘门将新的状态和旧的状态相乘，输出门将新的状态和旧的状态相加，这样保证了更新状态时误差的恒定，因此适应了不同时间跨度的预测，LSTM有能力学习更长步长的输入序列。LSTM通过门控机制和逐位相乘的Hadamard积使网络更新过程中的权值不会过大，同时保留的长期信息也避免了累乘放大的问题。因此，LSTM通常用于解决与时间序列问题相关的应用场合。

LSTM时间序列特征提取的网络设计如图4所示，具体如下：

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 LSTM网络设计

Fig. 4 LSTM network design

1）LSTM实现风电功率时序特征的提取和训练，由16个LSTM记忆细胞构成，其中遗忘门对上一时刻状态选择遗忘的程度，输入门选择当前阶段输入的程度，输出门选择哪些状态作为当前隐藏状态的输出。

2）前面的全连接层负责将LSTM输出进行分类，后面的全连接层负责回归，完成风电功率的最终预测和输出，激活函数为sigmoid，2层神经元数目分别是128与96。

3 基于MFE-CNN-LSTM的风电功率混合预测模型

3.1 总体网络架构设计

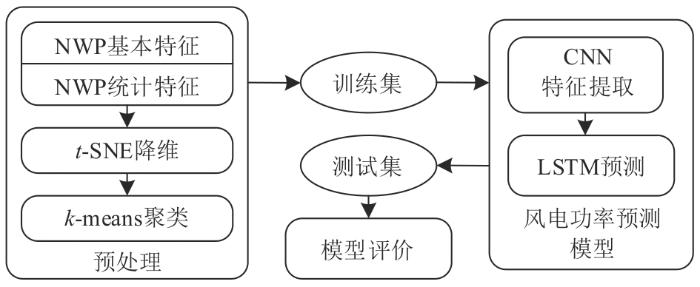
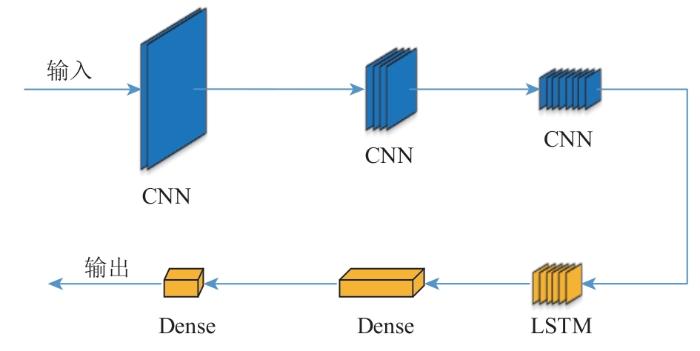
MFE-CNN-LSTM网络是一种在时间维度深度挖掘数据特征的深度学习模型，MFE-CNN- LSTM模型预测框架如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 MFE-CNN-LSTM模型预测框架图

Fig. 5 Diagram of MFE-CNN-LSTM model prediction framework

网络的输入是3个类别的172维特征向量，输出的是未来1天(96个时刻点)的风电功率。不同于单独的CNN网络和LSTM神经网络，以CNN作为特征提取器，防止LSTM预测多维序列时梯度弥散；LSTM作为预测器，有利于对长时序列的信息保留，将CNN用于风电功率的特征提取，其结果输入至LSTM，输出为预测功率，结构如图6所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 MFE-CNN-LSTM结构图

Fig. 6 Diagram of MFE-CNN-LSTM structure

模型结构主要包括3层卷积层、1层LSTM层及2个全连接层，输入为672×172的维度，输出为96×1的维度。

3.2 网络训练过程

本文所提方法首先将1年的NWP数据进行基本特征和统计性特征提取，共提取了184个特征量，然后用t-SNE将特征量降维到两维量，接着再进行聚类，可得到3组数据；在各类别数据中分别用672个时刻点的172个输入特征作为MFE-CNN-LSTM预测模型的输入；用1年数据中80%的数据来训练预测模型，将训练集中10%数据组成的验证集的损失函数降到可接受范围，并用提前终止训练策略防止过拟合，得到3个预测模型；根据预测日(即10%测试集)的类别选用不同的预测模型进行风电功率预测。

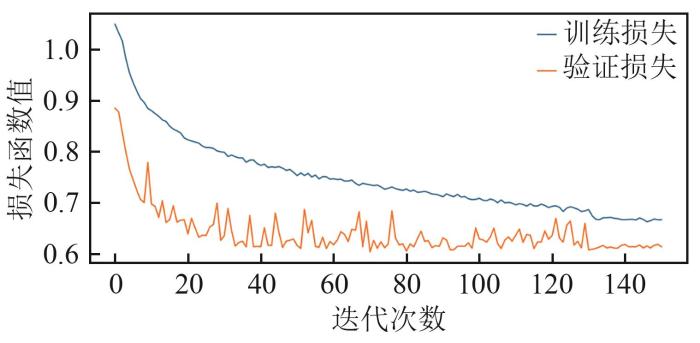
另外，深度训练的模型可能会因为输入数据不足或过度训练导致过拟合的问题，即测试集的预测效果远不及训练集。当数据集非常大时，尤其容易出现这种测试集误差由大到小再反弹的过程。此处采用提前停止训练的方法解决此问题，这是深度学习中常用的正则化方法，易操作且有效，它基本上不会改变基本训练过程、代价函数以及最终参数值的获取过程。停止的时刻是训练集损失继续减少而验证集损失增加时，因为此时已存在过拟合。实验部分根据每个模型的训练情况选择了一个不会产生过拟合的时刻值，并让每个对比模型都根据这个时刻停止训练，以保证性能比较的公平性。

预测过程的损失函数值与迭代次数的关系如图7所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 损失函数变化曲线

Fig. 7 Variation curve of loss function

4 实例分析

4.1 针对多特征提取的消融实验

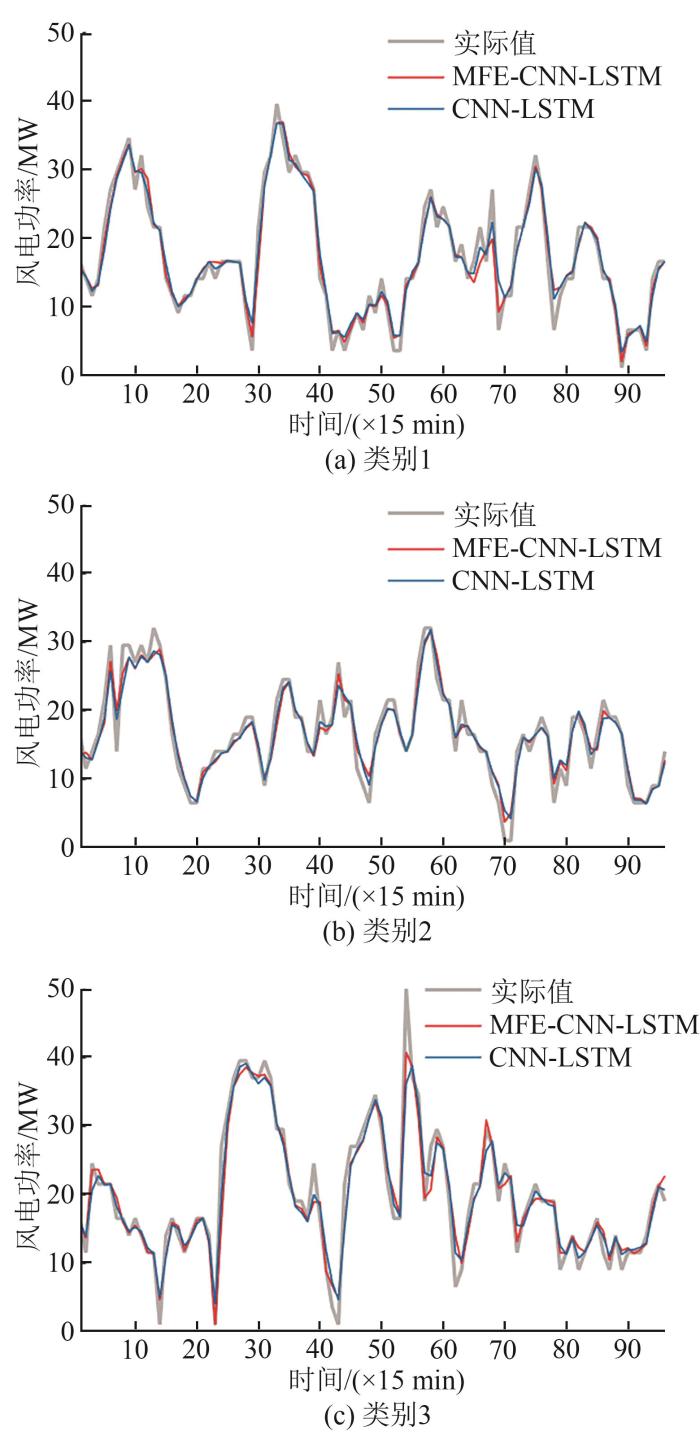
为了验证所提MFE-CNN-LSTM预测模型中的MFE部分是否发挥了提升预测性能的作用，对MFE网络进行了消融分析，以CNN-LSTM模型作为对比，预测误差如表3所示。表中e_MSE为均方误差，e_RMSE为均方根误差，e_MAE为平均绝对误差，e_MRE为相对平均误差。

表3 多特征提取消融误差

Tab. 3 Multi-feature extraction ablation errors

类别	模型	e_MSE/MW	e_RMSE/MW	e_MAE/MW	e_MRE/ %
1	CNN-LSTM	3.626 8	1.904 4	1.460 4	15.312
1	MFE-CNN-LSTM	3.575 5	1.890 9	1.338 2	11.663
2	CNN-LSTM	3.710 1	1.926 2	1.499 6	17.413
2	MFE-CNN-LSTM	3.651 9	1.911 0	1.479 8	16.747
3	CNN-LSTM	6.500 5	2.549 6	1.732 2	20.924
3	MFE-CNN-LSTM	6.389 6	2.527 8	1.641 9	17.332

新窗口打开| 下载CSV

由表3可知，类别3的各误差指标值均明显大于类别1和类别2，这可能是由于不同类别原始数据特征存在的差异，导致同一预测模型对不同类别数据进行预测时的预测误差存在差异。

图8为多特征提取消融实验结果，可以看出类别3的实际风电功率波动幅度明显大于类别1和类别2。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 多特征提取消融实验

Fig. 8 Multi-feature extraction ablation experiments

另外，MFE-CNN-LSTM的误差指标基本上优于同一类别的CNN-LSTM预测模型，因此，从3种类别的风电功率预测结果可见，MFE起到了提升预测模型精度的作用，说明选取的NWP特征能够提高预测模型捕捉特征的效果。

4.2 针对CNN网络的消融实验

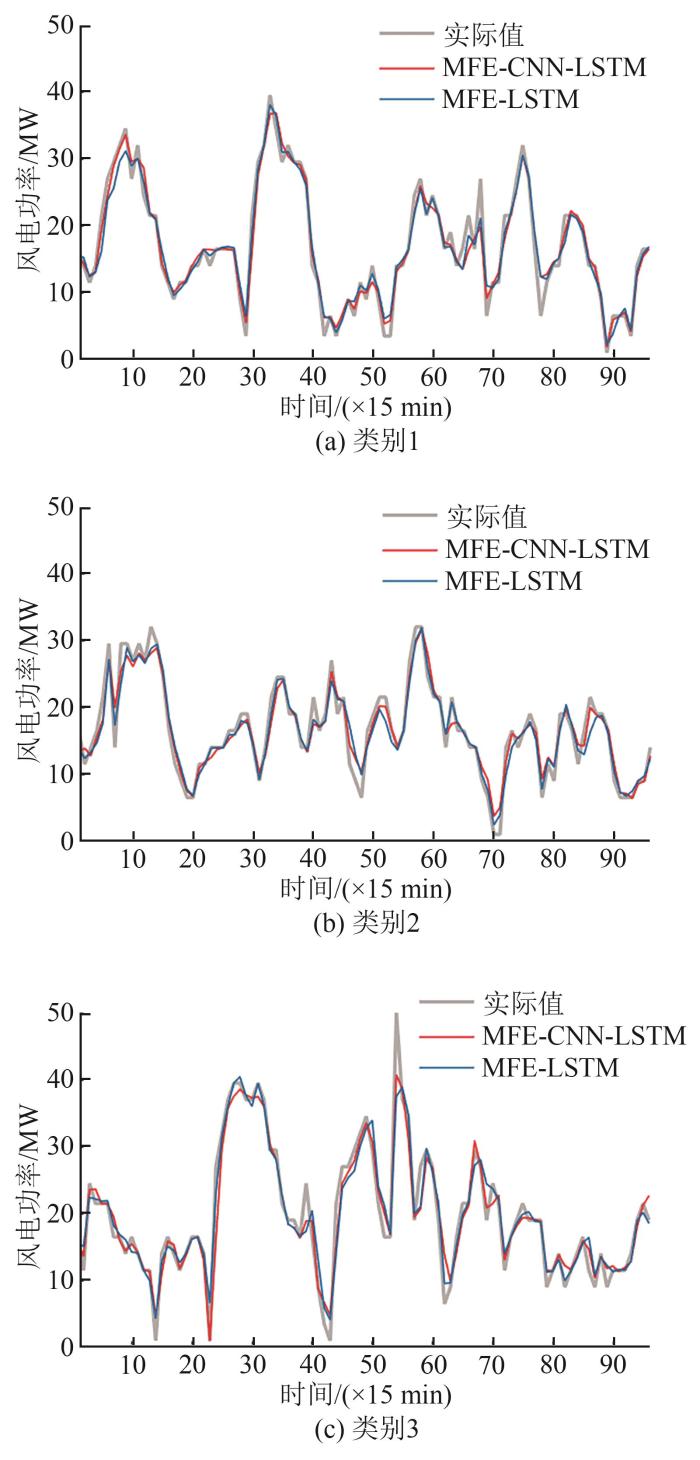
为了验证所提MFE-CNN-LSTM预测模型中的CNN网络部分是否发挥了提升预测性能的作用，对CNN网络进行消融分析，以MFE-LSTM模型作为对比模型，预测误差如表4所示。

表4 CNN网络消融误差

Tab. 4 CNN network ablation errors

类别	模型	e_MSE/MW	e_RMSE/MW	e_MAE/MW	e_MRE/%
1	MFE-LSTM	3.692 3	1.921 5	1.415 1	13.806
1	MFE-CNN-LSTM	3.575 5	1.890 9	1.338 2	11.663
2	MFE-LSTM	3.869 1	1.967 0	1.466 4	13.951
2	MFE-CNN-LSTM	3.651 9	1.911 0	1.479 8	16.747
3	MFE-LSTM	6.865 4	2.620 2	1.713 4	21.924
3	MFE-CNN-LSTM	6.389 6	2.527 8	1.641 9	17.332

新窗口打开| 下载CSV

从整体上看，类别1和类别2的预测效果相较类别3更好，相差较大的是均方误差及相对平均误差。从图9的实际功率曲线中可直观推断类别3误差更大的原因在于其波动性较大，有很多突变的时刻，但总体上预测误差都在合理范围内。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 CNN网络消融实验

Fig. 9 CNN network ablation experiments

同一类别中，采用CNN网络部分的MFE-CNN-LSTM预测模型预测效果均优于不采用CNN进行特征提取的MFE-LSTM网络，说明CNN网络有助于对输入数据进行特征的再提取，提取的特征是有效的。

4.3 MFE-CNN-LSTM与其他预测模型的对比

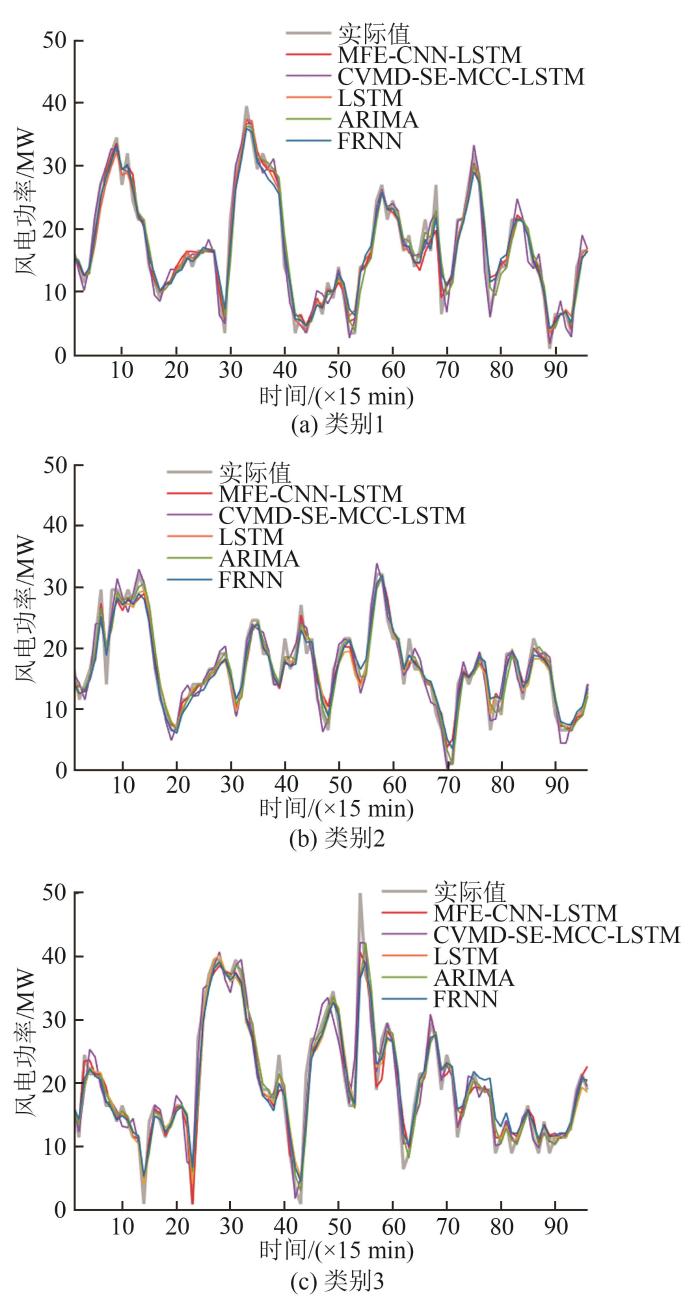
图10为MFE-CNN-LSTM预测模型与ARIMA、LSTM、FRNN和CVMD-SE-MCC-LSTM预测模型的预测效果对比，3种聚类类别各预测1天，误差如表5所示。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 不同预测模型的预测结果对比

Fig. 10 Comparison of prediction results for different prediction models

表5 各风电功率预测模型误差对比

Tab. 5 Comparison of errors of different wind power prediction models

类别	模型	e_MSE/ MW	e_RMSE/ MW	e_MAE/ MW	e_MRE/ %
1	ARIMA	5.043 8	2.245 8	1.711 2	17.350
	FRNN	3.925 9	1.981 4	1.550 0	16.979
	LSTM	3.754 9	1.937 8	1.465 3	15.784
	CVMD-SE-MCC-LSTM	3.672 5	1.916 4	1.500 0	13.154
	MFE-CNN-LSTM	3.575 5	1.890 9	1.338 2	11.663
2	ARIMA	4.405 7	2.099 0	1.613 6	13.061
	FRNN	3.856 1	1.963 7	1.575 9	17.328
	LSTM	3.952 9	1.988 2	1.579 7	16.878
	CVMD-SE-MCC-LSTM	3.787 2	1.946 1	1.494 7	12.128
	MFE-CNN-LSTM	3.651 9	1.911 0	1.479 8	16.747
3	ARIMA	8.418 5	2.901 5	1.956 1	22.777
	FRNN	7.360 8	2.713 1	1.883 4	25.111
	LSTM	7.012 9	2.648 2	1.812 9	21.634
	CVMD-SE-MCC-LSTM	6.662 9	2.581 3	1.955 3	23.920
	MFE-CNN-LSTM	6.389 6	2.527 8	1.641 9	17.332

新窗口打开| 下载CSV

从图10和表5可知，在大部分情况下，MFE-CNN-LSTM都有较好的表现。当实际功率不稳定时，大多模型都不能跟踪到真实趋势，所以有混沌的表现。

总的来说，ARIMA预测模型相对实际值有明显的滞后，FRNN和LSTM预测模型比较稳定和准确，CVMD-SE-MCC-LSTM预测模型在3种聚类类型中的均方误差比LSTM预测方法低，但是在功率变化率较大的时刻存在超调的现象，而MFE-CNN-LSTM风电功率预测模型的预测功率与实际功率趋势更贴合。由于测试集对于模型是全新的数据，因此能够有效反映所提MFE-CNN-LSTM模型的泛化能力；采用同一数据集对比CVMD-SE-MCC-LSTM预测模型和MFE-CNN-LSTM预测模型，可有效反映MFE-CNN-LSTM预测方法在波动性较大场合下的功率预测能力，预测1天功率的均方误差相比CVMD-SE-MCC-LSTM预测模型平均降低了3.44%。

5 结论

基于MFE-CNN-LSTM的风电功率预测模型，设计了适用于短期预测的输入模式和CNN-LSTM网络架构，得出以下结论：

1）MFE-CNN-LSTM模型提升了LSTM模型对数值天气预报的特征提取能力，提高了预测模型捕捉特征的效果；

2）CNN层在MFE-CNN-LSTM模型中，起到提升功率特征提取性能的作用，对其他领域时序预测的研究具备参考价值；

3）MFE-CNN-LSTM预测模型在不稳定时序数据预测场景下，预测效果优于ARIMA、FRNN、LSTM和CVMD-SE-MCC-LSTM预测模型。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

张丽英，叶廷路，辛耀中，等．

大规模风电接入电网的相关问题及措施

[J]．中国电机工程学报，2010，30(25)：1-9．