World energy outlook 2017
1
2017
... 2017年世界能源展望报告指出,光伏发电年增幅首次超过了风电[1].随着2021年我国碳达峰、碳中和目标及一系列政策出台,我国光伏发电迎来其发展的重大机遇期[2-3],新增开发规模达历史新高,新建项目全面实现平价上网,发电利用率维持较高水平.但是光伏发电大规模并网下其功率的不确定性也给电网调度、电力市场的稳定和安全带来挑战[4-6],而对光伏功率不确定性进行精细地刻画为应对这些挑战提供了技术支撑[7]. ...
光伏发电系统发电功率预测
1
2020
... 2017年世界能源展望报告指出,光伏发电年增幅首次超过了风电[1].随着2021年我国碳达峰、碳中和目标及一系列政策出台,我国光伏发电迎来其发展的重大机遇期[2-3],新增开发规模达历史新高,新建项目全面实现平价上网,发电利用率维持较高水平.但是光伏发电大规模并网下其功率的不确定性也给电网调度、电力市场的稳定和安全带来挑战[4-6],而对光伏功率不确定性进行精细地刻画为应对这些挑战提供了技术支撑[7]. ...
Power forecasting of photovoltaic power generation system
1
2020
... 2017年世界能源展望报告指出,光伏发电年增幅首次超过了风电[1].随着2021年我国碳达峰、碳中和目标及一系列政策出台,我国光伏发电迎来其发展的重大机遇期[2-3],新增开发规模达历史新高,新建项目全面实现平价上网,发电利用率维持较高水平.但是光伏发电大规模并网下其功率的不确定性也给电网调度、电力市场的稳定和安全带来挑战[4-6],而对光伏功率不确定性进行精细地刻画为应对这些挑战提供了技术支撑[7]. ...
区域光伏发电出力特性分析研究
1
2022
... 2017年世界能源展望报告指出,光伏发电年增幅首次超过了风电[1].随着2021年我国碳达峰、碳中和目标及一系列政策出台,我国光伏发电迎来其发展的重大机遇期[2-3],新增开发规模达历史新高,新建项目全面实现平价上网,发电利用率维持较高水平.但是光伏发电大规模并网下其功率的不确定性也给电网调度、电力市场的稳定和安全带来挑战[4-6],而对光伏功率不确定性进行精细地刻画为应对这些挑战提供了技术支撑[7]. ...
Analysis and research on output characteristics of regional photovoltaic power generation
1
2022
... 2017年世界能源展望报告指出,光伏发电年增幅首次超过了风电[1].随着2021年我国碳达峰、碳中和目标及一系列政策出台,我国光伏发电迎来其发展的重大机遇期[2-3],新增开发规模达历史新高,新建项目全面实现平价上网,发电利用率维持较高水平.但是光伏发电大规模并网下其功率的不确定性也给电网调度、电力市场的稳定和安全带来挑战[4-6],而对光伏功率不确定性进行精细地刻画为应对这些挑战提供了技术支撑[7]. ...
高比例光伏发电对浙江电网电力平衡的影响及应对策略
1
2022
... 2017年世界能源展望报告指出,光伏发电年增幅首次超过了风电[1].随着2021年我国碳达峰、碳中和目标及一系列政策出台,我国光伏发电迎来其发展的重大机遇期[2-3],新增开发规模达历史新高,新建项目全面实现平价上网,发电利用率维持较高水平.但是光伏发电大规模并网下其功率的不确定性也给电网调度、电力市场的稳定和安全带来挑战[4-6],而对光伏功率不确定性进行精细地刻画为应对这些挑战提供了技术支撑[7]. ...
The impact of high-proportion photovoltaic power generation on the power balance of Zhejiang power grid and its countermeasures
1
2022
... 2017年世界能源展望报告指出,光伏发电年增幅首次超过了风电[1].随着2021年我国碳达峰、碳中和目标及一系列政策出台,我国光伏发电迎来其发展的重大机遇期[2-3],新增开发规模达历史新高,新建项目全面实现平价上网,发电利用率维持较高水平.但是光伏发电大规模并网下其功率的不确定性也给电网调度、电力市场的稳定和安全带来挑战[4-6],而对光伏功率不确定性进行精细地刻画为应对这些挑战提供了技术支撑[7]. ...
Research on application of photovoltaic power generation system in thermal power plant
0
2022
基于时变因素的光伏发电系统可靠性评估
1
2023
... 2017年世界能源展望报告指出,光伏发电年增幅首次超过了风电[1].随着2021年我国碳达峰、碳中和目标及一系列政策出台,我国光伏发电迎来其发展的重大机遇期[2-3],新增开发规模达历史新高,新建项目全面实现平价上网,发电利用率维持较高水平.但是光伏发电大规模并网下其功率的不确定性也给电网调度、电力市场的稳定和安全带来挑战[4-6],而对光伏功率不确定性进行精细地刻画为应对这些挑战提供了技术支撑[7]. ...
Reliability evaluation of photovoltaic system based on time varying factors
1
2023
... 2017年世界能源展望报告指出,光伏发电年增幅首次超过了风电[1].随着2021年我国碳达峰、碳中和目标及一系列政策出台,我国光伏发电迎来其发展的重大机遇期[2-3],新增开发规模达历史新高,新建项目全面实现平价上网,发电利用率维持较高水平.但是光伏发电大规模并网下其功率的不确定性也给电网调度、电力市场的稳定和安全带来挑战[4-6],而对光伏功率不确定性进行精细地刻画为应对这些挑战提供了技术支撑[7]. ...
基于PCA-LMD-WOA-ELM的短期光伏功率预测
1
2022
... 2017年世界能源展望报告指出,光伏发电年增幅首次超过了风电[1].随着2021年我国碳达峰、碳中和目标及一系列政策出台,我国光伏发电迎来其发展的重大机遇期[2-3],新增开发规模达历史新高,新建项目全面实现平价上网,发电利用率维持较高水平.但是光伏发电大规模并网下其功率的不确定性也给电网调度、电力市场的稳定和安全带来挑战[4-6],而对光伏功率不确定性进行精细地刻画为应对这些挑战提供了技术支撑[7]. ...
Short term photovoltaic power prediction based on PCA-LMD-WOA-ELM
1
2022
... 2017年世界能源展望报告指出,光伏发电年增幅首次超过了风电[1].随着2021年我国碳达峰、碳中和目标及一系列政策出台,我国光伏发电迎来其发展的重大机遇期[2-3],新增开发规模达历史新高,新建项目全面实现平价上网,发电利用率维持较高水平.但是光伏发电大规模并网下其功率的不确定性也给电网调度、电力市场的稳定和安全带来挑战[4-6],而对光伏功率不确定性进行精细地刻画为应对这些挑战提供了技术支撑[7]. ...
A review and evaluation of the state-of-the-art in PV solar power forecasting:techniques and optimization
2
2020
... 研究表明,与光伏功率相关程度最大的因素为地表太阳辐照度,其中地理位置和季节是影响太阳辐照度的确定性因素,而云遮盖和云运动是影响太阳辐射最主要的不确定性原因[8].根据预测时长不同,光伏功率预测包括超短期预测(15 min 至4 h)、短期预测(4 h至3 d)、中期预测 (3 d 至1个月)和长期预测(1个月以上)[9],考虑到超过24~48 h的云状态及气象预测不具备参考性,故基于气象因素的光伏功率预测一般为日前、日内或更小时间尺度的预测.日前或日内光伏出力预测通常采用天气分型技术[10-12],小时级光伏功率预测有时也利用卫星或地表的云图像辅助预测[13]. ...
... 天气分型是光伏功率预测中不可或缺的一个预处理步骤,特别是对提高日前光伏功率预测精度有显著效果[8].一部分学者基于权威气象定义展开天气分型的功率预测研究,如叶林等[14]参照短期天气预报的国家标准及气象学基本原理,利用数值天气预报(numeric weather prediction,NWP)的云量和降水指标,将天气划分为5种类型,随后采用变分模态分解和深度学习结合的方法建立不同天气类型的功率预测模型.Wang等[12]将33种标准天气类型重新划分为10种,训练以辐照度为输入、10种天气类型为输出的天气分类模型,利用该天气分类模型进而实施分天气类型的功率预测建模. ...
1
2014
... 研究表明,与光伏功率相关程度最大的因素为地表太阳辐照度,其中地理位置和季节是影响太阳辐照度的确定性因素,而云遮盖和云运动是影响太阳辐射最主要的不确定性原因[8].根据预测时长不同,光伏功率预测包括超短期预测(15 min 至4 h)、短期预测(4 h至3 d)、中期预测 (3 d 至1个月)和长期预测(1个月以上)[9],考虑到超过24~48 h的云状态及气象预测不具备参考性,故基于气象因素的光伏功率预测一般为日前、日内或更小时间尺度的预测.日前或日内光伏出力预测通常采用天气分型技术[10-12],小时级光伏功率预测有时也利用卫星或地表的云图像辅助预测[13]. ...
1
2014
... 研究表明,与光伏功率相关程度最大的因素为地表太阳辐照度,其中地理位置和季节是影响太阳辐照度的确定性因素,而云遮盖和云运动是影响太阳辐射最主要的不确定性原因[8].根据预测时长不同,光伏功率预测包括超短期预测(15 min 至4 h)、短期预测(4 h至3 d)、中期预测 (3 d 至1个月)和长期预测(1个月以上)[9],考虑到超过24~48 h的云状态及气象预测不具备参考性,故基于气象因素的光伏功率预测一般为日前、日内或更小时间尺度的预测.日前或日内光伏出力预测通常采用天气分型技术[10-12],小时级光伏功率预测有时也利用卫星或地表的云图像辅助预测[13]. ...
光伏发电出力的条件预测误差概率分布估计方法
2
2015
... 研究表明,与光伏功率相关程度最大的因素为地表太阳辐照度,其中地理位置和季节是影响太阳辐照度的确定性因素,而云遮盖和云运动是影响太阳辐射最主要的不确定性原因[8].根据预测时长不同,光伏功率预测包括超短期预测(15 min 至4 h)、短期预测(4 h至3 d)、中期预测 (3 d 至1个月)和长期预测(1个月以上)[9],考虑到超过24~48 h的云状态及气象预测不具备参考性,故基于气象因素的光伏功率预测一般为日前、日内或更小时间尺度的预测.日前或日内光伏出力预测通常采用天气分型技术[10-12],小时级光伏功率预测有时也利用卫星或地表的云图像辅助预测[13]. ...
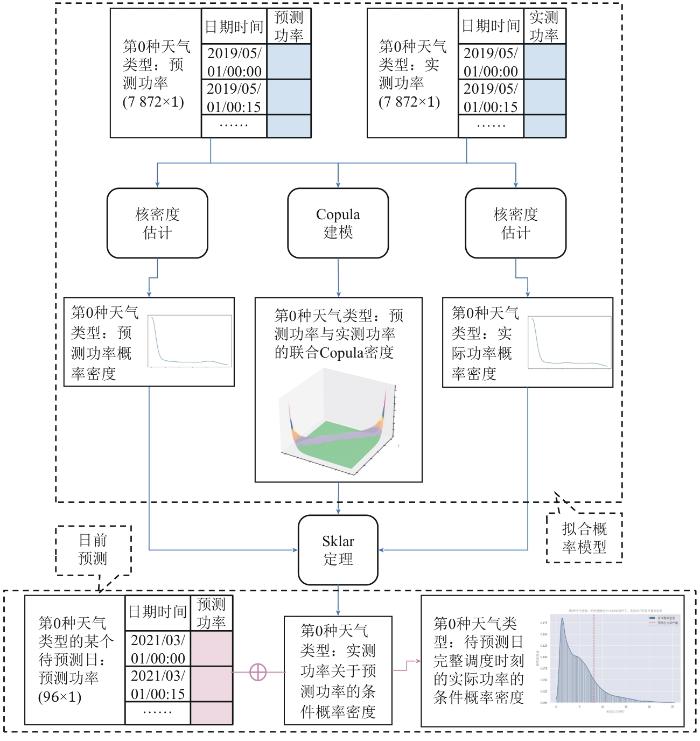
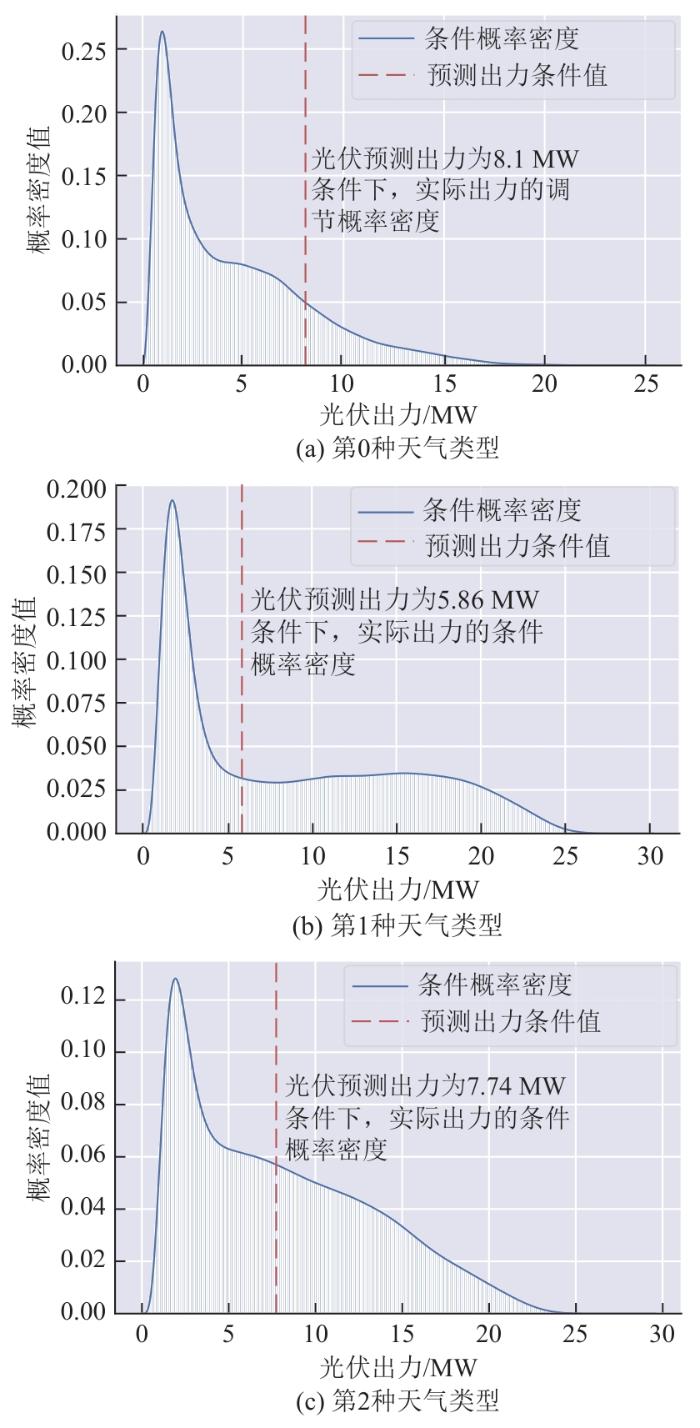
... 对功率的概率刻画主要包含功率或预测误差的分位数、置信区间、典型场景、概率分布等,但因概率分布与随机变量相互唯一确定,且概率分布可以导出区间预测、场景等其他信息,在应用上更具优势.此外,就功率的概率建模而言,相较于直接统计或拟合功率、功率预测误差的分布,拟合功率的条件概率分布在理论上更精确[10,33].因此,本节以核密度估计[34]和Copula理论[35]为工具,建立实际功率关于预测功率的条件概率模型.此模型的输入为预测功率、实际功率,输出为实际功率关于预测功率的条件概率分布.光伏功率的条件概率建模及日前预测的具体步骤如下:首先利用本文所提的二模态天气分类模型对待预测日的天气类型进行预测;然后筛选对应天气类型的历史预测功率、实测功率数据进行条件概率建模;最后根据待预测日的预测功率,计算出完整调度时刻实际功率的条件概率密度.以待预测日为第0种天气类型为例,构建光伏功率的条件概率模型,其日前预测框架如图5所示. ...
A method of probabilistic distribution estimation of conditional forecast error for photovoltaic power generation
2
2015
... 研究表明,与光伏功率相关程度最大的因素为地表太阳辐照度,其中地理位置和季节是影响太阳辐照度的确定性因素,而云遮盖和云运动是影响太阳辐射最主要的不确定性原因[8].根据预测时长不同,光伏功率预测包括超短期预测(15 min 至4 h)、短期预测(4 h至3 d)、中期预测 (3 d 至1个月)和长期预测(1个月以上)[9],考虑到超过24~48 h的云状态及气象预测不具备参考性,故基于气象因素的光伏功率预测一般为日前、日内或更小时间尺度的预测.日前或日内光伏出力预测通常采用天气分型技术[10-12],小时级光伏功率预测有时也利用卫星或地表的云图像辅助预测[13]. ...
... 对功率的概率刻画主要包含功率或预测误差的分位数、置信区间、典型场景、概率分布等,但因概率分布与随机变量相互唯一确定,且概率分布可以导出区间预测、场景等其他信息,在应用上更具优势.此外,就功率的概率建模而言,相较于直接统计或拟合功率、功率预测误差的分布,拟合功率的条件概率分布在理论上更精确[10,33].因此,本节以核密度估计[34]和Copula理论[35]为工具,建立实际功率关于预测功率的条件概率模型.此模型的输入为预测功率、实际功率,输出为实际功率关于预测功率的条件概率分布.光伏功率的条件概率建模及日前预测的具体步骤如下:首先利用本文所提的二模态天气分类模型对待预测日的天气类型进行预测;然后筛选对应天气类型的历史预测功率、实测功率数据进行条件概率建模;最后根据待预测日的预测功率,计算出完整调度时刻实际功率的条件概率密度.以待预测日为第0种天气类型为例,构建光伏功率的条件概率模型,其日前预测框架如图5所示. ...
Solar spectral influence on the performance of photovoltaic (PV) modules under fine weather and cloudy weather conditions
0
2013
Generative adversarial networks and convolutional neural networks based weather classification model for day ahead short-term photovoltaic power forecasting
3
2019
... 研究表明,与光伏功率相关程度最大的因素为地表太阳辐照度,其中地理位置和季节是影响太阳辐照度的确定性因素,而云遮盖和云运动是影响太阳辐射最主要的不确定性原因[8].根据预测时长不同,光伏功率预测包括超短期预测(15 min 至4 h)、短期预测(4 h至3 d)、中期预测 (3 d 至1个月)和长期预测(1个月以上)[9],考虑到超过24~48 h的云状态及气象预测不具备参考性,故基于气象因素的光伏功率预测一般为日前、日内或更小时间尺度的预测.日前或日内光伏出力预测通常采用天气分型技术[10-12],小时级光伏功率预测有时也利用卫星或地表的云图像辅助预测[13]. ...
... 天气分型是光伏功率预测中不可或缺的一个预处理步骤,特别是对提高日前光伏功率预测精度有显著效果[8].一部分学者基于权威气象定义展开天气分型的功率预测研究,如叶林等[14]参照短期天气预报的国家标准及气象学基本原理,利用数值天气预报(numeric weather prediction,NWP)的云量和降水指标,将天气划分为5种类型,随后采用变分模态分解和深度学习结合的方法建立不同天气类型的功率预测模型.Wang等[12]将33种标准天气类型重新划分为10种,训练以辐照度为输入、10种天气类型为输出的天气分类模型,利用该天气分类模型进而实施分天气类型的功率预测建模. ...
... 1)从理论上来说,针对光伏预测中的天气分类问题,一种普遍做法是:建立NWP为输入、天气类型为输出的分类或聚类模型[14,18,24].但该方法很大程度上依赖预测气象的准确度,而NWP通常偏差较大,这会导致模型学到虚假的对应关系,降低模型的鲁棒性.另一种普遍做法是:首先使用实测气象训练天气分类模型,然后构建各天气类型下的功率预测模型,最后将预测日对应的NWP气象指标输入到训练好的天气分类模型,得到预测日的天气类型,进而进行天气功率预测[12,20,25].但该思路存在模型迁移问题:其一,训练的天气分类模型对天气的界定和公共气象服务对天气的界定机制不一致;其二,实测气象指标和NWP气象指标存在分布差异.上述2个模型迁移问题均会导致天气分类预测模型的实际预测性能降低.因此,为克服天气分类中存在的模型迁移问题,减小天气分类模型对NWP精准度的依赖性,提高功率预测的准确度和鲁棒性,本研究提出二模态天气分类模型. ...
Image phase shift invariance based cloud motion displacement vector calculation method for ultra-short-term solar PV power forecasting
1
2018
... 研究表明,与光伏功率相关程度最大的因素为地表太阳辐照度,其中地理位置和季节是影响太阳辐照度的确定性因素,而云遮盖和云运动是影响太阳辐射最主要的不确定性原因[8].根据预测时长不同,光伏功率预测包括超短期预测(15 min 至4 h)、短期预测(4 h至3 d)、中期预测 (3 d 至1个月)和长期预测(1个月以上)[9],考虑到超过24~48 h的云状态及气象预测不具备参考性,故基于气象因素的光伏功率预测一般为日前、日内或更小时间尺度的预测.日前或日内光伏出力预测通常采用天气分型技术[10-12],小时级光伏功率预测有时也利用卫星或地表的云图像辅助预测[13]. ...
基于天气分型的短期光伏功率组合预测方法
3
2021
... 天气分型是光伏功率预测中不可或缺的一个预处理步骤,特别是对提高日前光伏功率预测精度有显著效果[8].一部分学者基于权威气象定义展开天气分型的功率预测研究,如叶林等[14]参照短期天气预报的国家标准及气象学基本原理,利用数值天气预报(numeric weather prediction,NWP)的云量和降水指标,将天气划分为5种类型,随后采用变分模态分解和深度学习结合的方法建立不同天气类型的功率预测模型.Wang等[12]将33种标准天气类型重新划分为10种,训练以辐照度为输入、10种天气类型为输出的天气分类模型,利用该天气分类模型进而实施分天气类型的功率预测建模. ...
... 1)从理论上来说,针对光伏预测中的天气分类问题,一种普遍做法是:建立NWP为输入、天气类型为输出的分类或聚类模型[14,18,24].但该方法很大程度上依赖预测气象的准确度,而NWP通常偏差较大,这会导致模型学到虚假的对应关系,降低模型的鲁棒性.另一种普遍做法是:首先使用实测气象训练天气分类模型,然后构建各天气类型下的功率预测模型,最后将预测日对应的NWP气象指标输入到训练好的天气分类模型,得到预测日的天气类型,进而进行天气功率预测[12,20,25].但该思路存在模型迁移问题:其一,训练的天气分类模型对天气的界定和公共气象服务对天气的界定机制不一致;其二,实测气象指标和NWP气象指标存在分布差异.上述2个模型迁移问题均会导致天气分类预测模型的实际预测性能降低.因此,为克服天气分类中存在的模型迁移问题,减小天气分类模型对NWP精准度的依赖性,提高功率预测的准确度和鲁棒性,本研究提出二模态天气分类模型. ...
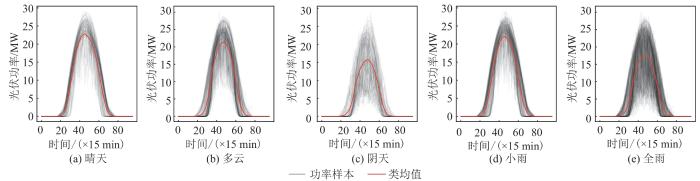
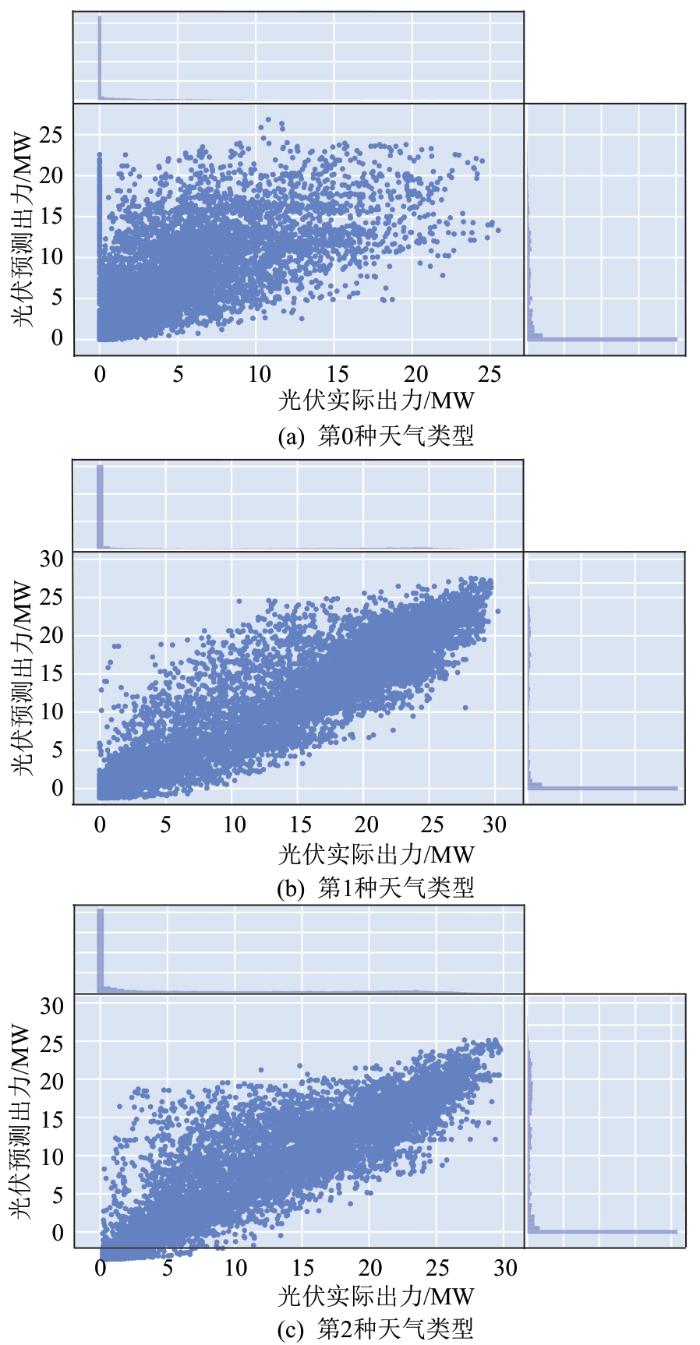
... 本文采用文献[14]中的天气分型方法,即使用NWP气象中的云量、降水指标对天气类型进行划分,图2为按照该方法划分的5种天气类型下的光伏功率.由图2可知:1)5种天气类型下均有不少的光伏功率峰值接近30 MW,包括在阴天和全雨天气类型下,这表明使用该方法划分的天气分型存在较大噪声;2)无论是从类均值曲线的峰值还是从样本曲线峰值的跨度上看,晴天、多云、小雨3个分类光伏功率模式区分不明显,同样地也难以区分阴天和全雨,这表明使用该分类方法模糊了类的界定,并未达到预定的划分5种类型天气的效果.总的来说,对于本文所采用的光伏电站,光伏功率模式并未在所划分的天气类型下显现特定的模式.其原因可能是:该NWP气象源的数据精度不理想,或这种天气类型划分方式并不是对所有电站有效.这也侧面说明本文有针对性地重新考虑天气分型方法在功率预测中的运用是有必要的. ...
Combination forecasting method of short-term photovoltaic power based on weather classification
3
2021
... 天气分型是光伏功率预测中不可或缺的一个预处理步骤,特别是对提高日前光伏功率预测精度有显著效果[8].一部分学者基于权威气象定义展开天气分型的功率预测研究,如叶林等[14]参照短期天气预报的国家标准及气象学基本原理,利用数值天气预报(numeric weather prediction,NWP)的云量和降水指标,将天气划分为5种类型,随后采用变分模态分解和深度学习结合的方法建立不同天气类型的功率预测模型.Wang等[12]将33种标准天气类型重新划分为10种,训练以辐照度为输入、10种天气类型为输出的天气分类模型,利用该天气分类模型进而实施分天气类型的功率预测建模. ...
... 1)从理论上来说,针对光伏预测中的天气分类问题,一种普遍做法是:建立NWP为输入、天气类型为输出的分类或聚类模型[14,18,24].但该方法很大程度上依赖预测气象的准确度,而NWP通常偏差较大,这会导致模型学到虚假的对应关系,降低模型的鲁棒性.另一种普遍做法是:首先使用实测气象训练天气分类模型,然后构建各天气类型下的功率预测模型,最后将预测日对应的NWP气象指标输入到训练好的天气分类模型,得到预测日的天气类型,进而进行天气功率预测[12,20,25].但该思路存在模型迁移问题:其一,训练的天气分类模型对天气的界定和公共气象服务对天气的界定机制不一致;其二,实测气象指标和NWP气象指标存在分布差异.上述2个模型迁移问题均会导致天气分类预测模型的实际预测性能降低.因此,为克服天气分类中存在的模型迁移问题,减小天气分类模型对NWP精准度的依赖性,提高功率预测的准确度和鲁棒性,本研究提出二模态天气分类模型. ...
... 本文采用文献[14]中的天气分型方法,即使用NWP气象中的云量、降水指标对天气类型进行划分,图2为按照该方法划分的5种天气类型下的光伏功率.由图2可知:1)5种天气类型下均有不少的光伏功率峰值接近30 MW,包括在阴天和全雨天气类型下,这表明使用该方法划分的天气分型存在较大噪声;2)无论是从类均值曲线的峰值还是从样本曲线峰值的跨度上看,晴天、多云、小雨3个分类光伏功率模式区分不明显,同样地也难以区分阴天和全雨,这表明使用该分类方法模糊了类的界定,并未达到预定的划分5种类型天气的效果.总的来说,对于本文所采用的光伏电站,光伏功率模式并未在所划分的天气类型下显现特定的模式.其原因可能是:该NWP气象源的数据精度不理想,或这种天气类型划分方式并不是对所有电站有效.这也侧面说明本文有针对性地重新考虑天气分型方法在功率预测中的运用是有必要的. ...
基于时间序列的深度学习光伏发电模型研究
1
2021
... 另一部分学者从数据挖掘角度,采用聚类[15-16]、主成分分析[17]等无监督学习方法划分天气类型.王勃等[18]对NWP数据进行主成分分析和系统谱聚类分析,将气象划分为4种类型,然后使用反向传播神经网络构建每种天气类型的功率预测模型;Chen等[19]使用自组织映射(self-organizing map,SOM)网络对数值天气指标进行聚类;李芬等[20]提出一个二阶段天气分析方法,该方法首先利用云量将天气划分为晴天和云天,然后根据云天综合气象因子,利用SOM将云天划分为3种子类型. ...
Deep learning photovoltaic power generation model based on time series
1
2021
... 另一部分学者从数据挖掘角度,采用聚类[15-16]、主成分分析[17]等无监督学习方法划分天气类型.王勃等[18]对NWP数据进行主成分分析和系统谱聚类分析,将气象划分为4种类型,然后使用反向传播神经网络构建每种天气类型的功率预测模型;Chen等[19]使用自组织映射(self-organizing map,SOM)网络对数值天气指标进行聚类;李芬等[20]提出一个二阶段天气分析方法,该方法首先利用云量将天气划分为晴天和云天,然后根据云天综合气象因子,利用SOM将云天划分为3种子类型. ...
基于模糊聚类分析的电能质量扰动模式识别方法
1
2022
... 另一部分学者从数据挖掘角度,采用聚类[15-16]、主成分分析[17]等无监督学习方法划分天气类型.王勃等[18]对NWP数据进行主成分分析和系统谱聚类分析,将气象划分为4种类型,然后使用反向传播神经网络构建每种天气类型的功率预测模型;Chen等[19]使用自组织映射(self-organizing map,SOM)网络对数值天气指标进行聚类;李芬等[20]提出一个二阶段天气分析方法,该方法首先利用云量将天气划分为晴天和云天,然后根据云天综合气象因子,利用SOM将云天划分为3种子类型. ...
Disturbance pattern recognition method of power quality based on the fuzzy clustering analysis
1
2022
... 另一部分学者从数据挖掘角度,采用聚类[15-16]、主成分分析[17]等无监督学习方法划分天气类型.王勃等[18]对NWP数据进行主成分分析和系统谱聚类分析,将气象划分为4种类型,然后使用反向传播神经网络构建每种天气类型的功率预测模型;Chen等[19]使用自组织映射(self-organizing map,SOM)网络对数值天气指标进行聚类;李芬等[20]提出一个二阶段天气分析方法,该方法首先利用云量将天气划分为晴天和云天,然后根据云天综合气象因子,利用SOM将云天划分为3种子类型. ...
基于主成分分析合作博弈的电网负荷智能预测方法研究
1
2022
... 另一部分学者从数据挖掘角度,采用聚类[15-16]、主成分分析[17]等无监督学习方法划分天气类型.王勃等[18]对NWP数据进行主成分分析和系统谱聚类分析,将气象划分为4种类型,然后使用反向传播神经网络构建每种天气类型的功率预测模型;Chen等[19]使用自组织映射(self-organizing map,SOM)网络对数值天气指标进行聚类;李芬等[20]提出一个二阶段天气分析方法,该方法首先利用云量将天气划分为晴天和云天,然后根据云天综合气象因子,利用SOM将云天划分为3种子类型. ...
A study on the intelligent load forecasting method of power grids based on principal component analysis and cooperative game
1
2022
... 另一部分学者从数据挖掘角度,采用聚类[15-16]、主成分分析[17]等无监督学习方法划分天气类型.王勃等[18]对NWP数据进行主成分分析和系统谱聚类分析,将气象划分为4种类型,然后使用反向传播神经网络构建每种天气类型的功率预测模型;Chen等[19]使用自组织映射(self-organizing map,SOM)网络对数值天气指标进行聚类;李芬等[20]提出一个二阶段天气分析方法,该方法首先利用云量将天气划分为晴天和云天,然后根据云天综合气象因子,利用SOM将云天划分为3种子类型. ...
基于天气分型的风电功率预测方法
2
2014
... 另一部分学者从数据挖掘角度,采用聚类[15-16]、主成分分析[17]等无监督学习方法划分天气类型.王勃等[18]对NWP数据进行主成分分析和系统谱聚类分析,将气象划分为4种类型,然后使用反向传播神经网络构建每种天气类型的功率预测模型;Chen等[19]使用自组织映射(self-organizing map,SOM)网络对数值天气指标进行聚类;李芬等[20]提出一个二阶段天气分析方法,该方法首先利用云量将天气划分为晴天和云天,然后根据云天综合气象因子,利用SOM将云天划分为3种子类型. ...
... 1)从理论上来说,针对光伏预测中的天气分类问题,一种普遍做法是:建立NWP为输入、天气类型为输出的分类或聚类模型[14,18,24].但该方法很大程度上依赖预测气象的准确度,而NWP通常偏差较大,这会导致模型学到虚假的对应关系,降低模型的鲁棒性.另一种普遍做法是:首先使用实测气象训练天气分类模型,然后构建各天气类型下的功率预测模型,最后将预测日对应的NWP气象指标输入到训练好的天气分类模型,得到预测日的天气类型,进而进行天气功率预测[12,20,25].但该思路存在模型迁移问题:其一,训练的天气分类模型对天气的界定和公共气象服务对天气的界定机制不一致;其二,实测气象指标和NWP气象指标存在分布差异.上述2个模型迁移问题均会导致天气分类预测模型的实际预测性能降低.因此,为克服天气分类中存在的模型迁移问题,减小天气分类模型对NWP精准度的依赖性,提高功率预测的准确度和鲁棒性,本研究提出二模态天气分类模型. ...
Study on weather typing based wind power prediction
2
2014
... 另一部分学者从数据挖掘角度,采用聚类[15-16]、主成分分析[17]等无监督学习方法划分天气类型.王勃等[18]对NWP数据进行主成分分析和系统谱聚类分析,将气象划分为4种类型,然后使用反向传播神经网络构建每种天气类型的功率预测模型;Chen等[19]使用自组织映射(self-organizing map,SOM)网络对数值天气指标进行聚类;李芬等[20]提出一个二阶段天气分析方法,该方法首先利用云量将天气划分为晴天和云天,然后根据云天综合气象因子,利用SOM将云天划分为3种子类型. ...
... 1)从理论上来说,针对光伏预测中的天气分类问题,一种普遍做法是:建立NWP为输入、天气类型为输出的分类或聚类模型[14,18,24].但该方法很大程度上依赖预测气象的准确度,而NWP通常偏差较大,这会导致模型学到虚假的对应关系,降低模型的鲁棒性.另一种普遍做法是:首先使用实测气象训练天气分类模型,然后构建各天气类型下的功率预测模型,最后将预测日对应的NWP气象指标输入到训练好的天气分类模型,得到预测日的天气类型,进而进行天气功率预测[12,20,25].但该思路存在模型迁移问题:其一,训练的天气分类模型对天气的界定和公共气象服务对天气的界定机制不一致;其二,实测气象指标和NWP气象指标存在分布差异.上述2个模型迁移问题均会导致天气分类预测模型的实际预测性能降低.因此,为克服天气分类中存在的模型迁移问题,减小天气分类模型对NWP精准度的依赖性,提高功率预测的准确度和鲁棒性,本研究提出二模态天气分类模型. ...
Online 24-h solar power forecasting based on weather type classification using artificial neural network
1
2011
... 另一部分学者从数据挖掘角度,采用聚类[15-16]、主成分分析[17]等无监督学习方法划分天气类型.王勃等[18]对NWP数据进行主成分分析和系统谱聚类分析,将气象划分为4种类型,然后使用反向传播神经网络构建每种天气类型的功率预测模型;Chen等[19]使用自组织映射(self-organizing map,SOM)网络对数值天气指标进行聚类;李芬等[20]提出一个二阶段天气分析方法,该方法首先利用云量将天气划分为晴天和云天,然后根据云天综合气象因子,利用SOM将云天划分为3种子类型. ...
一种新型天气分型方法及其在光伏功率预测中的应用
2
2021
... 另一部分学者从数据挖掘角度,采用聚类[15-16]、主成分分析[17]等无监督学习方法划分天气类型.王勃等[18]对NWP数据进行主成分分析和系统谱聚类分析,将气象划分为4种类型,然后使用反向传播神经网络构建每种天气类型的功率预测模型;Chen等[19]使用自组织映射(self-organizing map,SOM)网络对数值天气指标进行聚类;李芬等[20]提出一个二阶段天气分析方法,该方法首先利用云量将天气划分为晴天和云天,然后根据云天综合气象因子,利用SOM将云天划分为3种子类型. ...
... 1)从理论上来说,针对光伏预测中的天气分类问题,一种普遍做法是:建立NWP为输入、天气类型为输出的分类或聚类模型[14,18,24].但该方法很大程度上依赖预测气象的准确度,而NWP通常偏差较大,这会导致模型学到虚假的对应关系,降低模型的鲁棒性.另一种普遍做法是:首先使用实测气象训练天气分类模型,然后构建各天气类型下的功率预测模型,最后将预测日对应的NWP气象指标输入到训练好的天气分类模型,得到预测日的天气类型,进而进行天气功率预测[12,20,25].但该思路存在模型迁移问题:其一,训练的天气分类模型对天气的界定和公共气象服务对天气的界定机制不一致;其二,实测气象指标和NWP气象指标存在分布差异.上述2个模型迁移问题均会导致天气分类预测模型的实际预测性能降低.因此,为克服天气分类中存在的模型迁移问题,减小天气分类模型对NWP精准度的依赖性,提高功率预测的准确度和鲁棒性,本研究提出二模态天气分类模型. ...
A novel weather classification method and its application in photovoltaic power prediction
2
2021
... 另一部分学者从数据挖掘角度,采用聚类[15-16]、主成分分析[17]等无监督学习方法划分天气类型.王勃等[18]对NWP数据进行主成分分析和系统谱聚类分析,将气象划分为4种类型,然后使用反向传播神经网络构建每种天气类型的功率预测模型;Chen等[19]使用自组织映射(self-organizing map,SOM)网络对数值天气指标进行聚类;李芬等[20]提出一个二阶段天气分析方法,该方法首先利用云量将天气划分为晴天和云天,然后根据云天综合气象因子,利用SOM将云天划分为3种子类型. ...
... 1)从理论上来说,针对光伏预测中的天气分类问题,一种普遍做法是:建立NWP为输入、天气类型为输出的分类或聚类模型[14,18,24].但该方法很大程度上依赖预测气象的准确度,而NWP通常偏差较大,这会导致模型学到虚假的对应关系,降低模型的鲁棒性.另一种普遍做法是:首先使用实测气象训练天气分类模型,然后构建各天气类型下的功率预测模型,最后将预测日对应的NWP气象指标输入到训练好的天气分类模型,得到预测日的天气类型,进而进行天气功率预测[12,20,25].但该思路存在模型迁移问题:其一,训练的天气分类模型对天气的界定和公共气象服务对天气的界定机制不一致;其二,实测气象指标和NWP气象指标存在分布差异.上述2个模型迁移问题均会导致天气分类预测模型的实际预测性能降低.因此,为克服天气分类中存在的模型迁移问题,减小天气分类模型对NWP精准度的依赖性,提高功率预测的准确度和鲁棒性,本研究提出二模态天气分类模型. ...
Time-series clustering:a decade review
1
2015
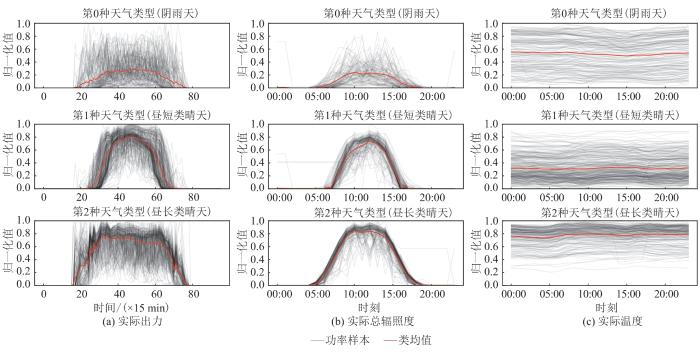
... 时间序列聚类是指基于相似性度量将时间序列聚合成不重叠的类,或划分为抽象的层次结构,使得类中的时间序列具有更大相似性,而类间的时间序列有更小的相似性,主要是用来挖掘和识别时间序列中感兴趣的模式[21].本文使用应用广泛的时间序列K均值聚类对光伏日功率曲线进行聚类. ...
Representation learning:a review and new perspectives
1
2013
... 多模态数据是指对于同一个描述对象,从不同领域或视角获取相关数据,然后把获取这些数据的每一个领域或视角叫做一个模态[22].在多模态数据中,每个模态能够为其余模态提供一定的信息,即模态之间存在一定的关联性,因此多模态学习即挖掘多模态数据间的相关联系以服务于特定背景和目的,有利于弥补单模态数据提供信息不充分的问题.子空间学习是一种得到充分研究和应用的多模态数据融合算法,该算法假设所有模态数据均可以投影到同一语义共享子空间,而在子空间内可以完成聚类、分类等数据挖掘任务[23]. ...
多模态数据融合算法研究
1
2018
... 多模态数据是指对于同一个描述对象,从不同领域或视角获取相关数据,然后把获取这些数据的每一个领域或视角叫做一个模态[22].在多模态数据中,每个模态能够为其余模态提供一定的信息,即模态之间存在一定的关联性,因此多模态学习即挖掘多模态数据间的相关联系以服务于特定背景和目的,有利于弥补单模态数据提供信息不充分的问题.子空间学习是一种得到充分研究和应用的多模态数据融合算法,该算法假设所有模态数据均可以投影到同一语义共享子空间,而在子空间内可以完成聚类、分类等数据挖掘任务[23]. ...
Research on multimodal data fusion methods
1
2018
... 多模态数据是指对于同一个描述对象,从不同领域或视角获取相关数据,然后把获取这些数据的每一个领域或视角叫做一个模态[22].在多模态数据中,每个模态能够为其余模态提供一定的信息,即模态之间存在一定的关联性,因此多模态学习即挖掘多模态数据间的相关联系以服务于特定背景和目的,有利于弥补单模态数据提供信息不充分的问题.子空间学习是一种得到充分研究和应用的多模态数据融合算法,该算法假设所有模态数据均可以投影到同一语义共享子空间,而在子空间内可以完成聚类、分类等数据挖掘任务[23]. ...
基于天气分型的风光出力互补性分析方法
1
2021
... 1)从理论上来说,针对光伏预测中的天气分类问题,一种普遍做法是:建立NWP为输入、天气类型为输出的分类或聚类模型[14,18,24].但该方法很大程度上依赖预测气象的准确度,而NWP通常偏差较大,这会导致模型学到虚假的对应关系,降低模型的鲁棒性.另一种普遍做法是:首先使用实测气象训练天气分类模型,然后构建各天气类型下的功率预测模型,最后将预测日对应的NWP气象指标输入到训练好的天气分类模型,得到预测日的天气类型,进而进行天气功率预测[12,20,25].但该思路存在模型迁移问题:其一,训练的天气分类模型对天气的界定和公共气象服务对天气的界定机制不一致;其二,实测气象指标和NWP气象指标存在分布差异.上述2个模型迁移问题均会导致天气分类预测模型的实际预测性能降低.因此,为克服天气分类中存在的模型迁移问题,减小天气分类模型对NWP精准度的依赖性,提高功率预测的准确度和鲁棒性,本研究提出二模态天气分类模型. ...
Analysis method for complementarity between wind and photovoltaic power outputs based on weather classification
1
2021
... 1)从理论上来说,针对光伏预测中的天气分类问题,一种普遍做法是:建立NWP为输入、天气类型为输出的分类或聚类模型[14,18,24].但该方法很大程度上依赖预测气象的准确度,而NWP通常偏差较大,这会导致模型学到虚假的对应关系,降低模型的鲁棒性.另一种普遍做法是:首先使用实测气象训练天气分类模型,然后构建各天气类型下的功率预测模型,最后将预测日对应的NWP气象指标输入到训练好的天气分类模型,得到预测日的天气类型,进而进行天气功率预测[12,20,25].但该思路存在模型迁移问题:其一,训练的天气分类模型对天气的界定和公共气象服务对天气的界定机制不一致;其二,实测气象指标和NWP气象指标存在分布差异.上述2个模型迁移问题均会导致天气分类预测模型的实际预测性能降低.因此,为克服天气分类中存在的模型迁移问题,减小天气分类模型对NWP精准度的依赖性,提高功率预测的准确度和鲁棒性,本研究提出二模态天气分类模型. ...
基于多尺度聚类分析的光伏功率特性建模及预测应用
1
2018
... 1)从理论上来说,针对光伏预测中的天气分类问题,一种普遍做法是:建立NWP为输入、天气类型为输出的分类或聚类模型[14,18,24].但该方法很大程度上依赖预测气象的准确度,而NWP通常偏差较大,这会导致模型学到虚假的对应关系,降低模型的鲁棒性.另一种普遍做法是:首先使用实测气象训练天气分类模型,然后构建各天气类型下的功率预测模型,最后将预测日对应的NWP气象指标输入到训练好的天气分类模型,得到预测日的天气类型,进而进行天气功率预测[12,20,25].但该思路存在模型迁移问题:其一,训练的天气分类模型对天气的界定和公共气象服务对天气的界定机制不一致;其二,实测气象指标和NWP气象指标存在分布差异.上述2个模型迁移问题均会导致天气分类预测模型的实际预测性能降低.因此,为克服天气分类中存在的模型迁移问题,减小天气分类模型对NWP精准度的依赖性,提高功率预测的准确度和鲁棒性,本研究提出二模态天气分类模型. ...
Multi-scale clustering analysis based modeling of photovoltaic power characteristics and its application in prediction
1
2018
... 1)从理论上来说,针对光伏预测中的天气分类问题,一种普遍做法是:建立NWP为输入、天气类型为输出的分类或聚类模型[14,18,24].但该方法很大程度上依赖预测气象的准确度,而NWP通常偏差较大,这会导致模型学到虚假的对应关系,降低模型的鲁棒性.另一种普遍做法是:首先使用实测气象训练天气分类模型,然后构建各天气类型下的功率预测模型,最后将预测日对应的NWP气象指标输入到训练好的天气分类模型,得到预测日的天气类型,进而进行天气功率预测[12,20,25].但该思路存在模型迁移问题:其一,训练的天气分类模型对天气的界定和公共气象服务对天气的界定机制不一致;其二,实测气象指标和NWP气象指标存在分布差异.上述2个模型迁移问题均会导致天气分类预测模型的实际预测性能降低.因此,为克服天气分类中存在的模型迁移问题,减小天气分类模型对NWP精准度的依赖性,提高功率预测的准确度和鲁棒性,本研究提出二模态天气分类模型. ...
Multimodal machine learning:a survey and taxonomy
1
2019
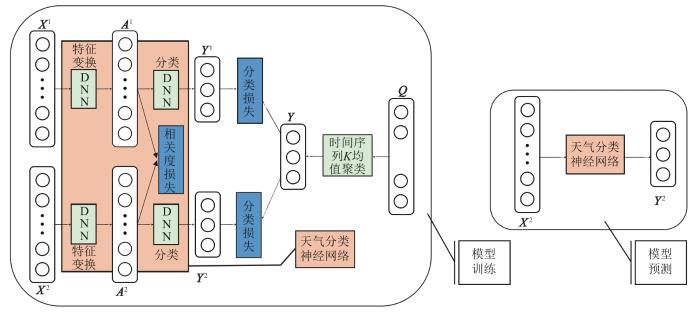
... 2)在实际应用中,多模态学习在语音合成、动作识别、医学图像融合、视频索引等任务的多个标准数据集上实现了最新的技术水平[26].特别是在电力领域,朱乔木[27]的研究和实验表明,相较于只考虑风速的风电功率预测,整合多种测量气象数据并挖掘其中有利于功率预测的信息,可以提高风电功率的预测精度;文献[28-29]的实验表明,相较于使用未处理的NWP数据、仅修正NWP系统误差后的数据以及传统的单点NWP修正数据,使用基于实测总辐照度修正的NWP总辐照度进行光伏功率预测的误差更小.本文提出二模态天气分类模型,其基本原理为,二模态的气象被投影到同一语义共享子空间.该子空间具有如下两方面特征:其一,子空间内的NWP气象与实测气象之间有更多的相关性;其二,子空间内NWP气象、实测气象有更高的天气分类准确度.其优化方法为:最大化NWP气象和实测气象的相关度量,最小化NWP气象和实测气象的分类精度,并将其作为损失函数训练天气分类模型.上述最大化2种气象相关度量可以视为模型利用实测气象对NWP气象进行修正,而最大化分类准确度则可以视为模型利用神经网络提取与天气类型有关的气象特征. ...
基于深度学习的电力系统暂态稳定评估及风电功率预测方法研究
1
2019
... 2)在实际应用中,多模态学习在语音合成、动作识别、医学图像融合、视频索引等任务的多个标准数据集上实现了最新的技术水平[26].特别是在电力领域,朱乔木[27]的研究和实验表明,相较于只考虑风速的风电功率预测,整合多种测量气象数据并挖掘其中有利于功率预测的信息,可以提高风电功率的预测精度;文献[28-29]的实验表明,相较于使用未处理的NWP数据、仅修正NWP系统误差后的数据以及传统的单点NWP修正数据,使用基于实测总辐照度修正的NWP总辐照度进行光伏功率预测的误差更小.本文提出二模态天气分类模型,其基本原理为,二模态的气象被投影到同一语义共享子空间.该子空间具有如下两方面特征:其一,子空间内的NWP气象与实测气象之间有更多的相关性;其二,子空间内NWP气象、实测气象有更高的天气分类准确度.其优化方法为:最大化NWP气象和实测气象的相关度量,最小化NWP气象和实测气象的分类精度,并将其作为损失函数训练天气分类模型.上述最大化2种气象相关度量可以视为模型利用实测气象对NWP气象进行修正,而最大化分类准确度则可以视为模型利用神经网络提取与天气类型有关的气象特征. ...
Research on power system transient stability assessment and wind power prediction method based on deep learning
1
2019
... 2)在实际应用中,多模态学习在语音合成、动作识别、医学图像融合、视频索引等任务的多个标准数据集上实现了最新的技术水平[26].特别是在电力领域,朱乔木[27]的研究和实验表明,相较于只考虑风速的风电功率预测,整合多种测量气象数据并挖掘其中有利于功率预测的信息,可以提高风电功率的预测精度;文献[28-29]的实验表明,相较于使用未处理的NWP数据、仅修正NWP系统误差后的数据以及传统的单点NWP修正数据,使用基于实测总辐照度修正的NWP总辐照度进行光伏功率预测的误差更小.本文提出二模态天气分类模型,其基本原理为,二模态的气象被投影到同一语义共享子空间.该子空间具有如下两方面特征:其一,子空间内的NWP气象与实测气象之间有更多的相关性;其二,子空间内NWP气象、实测气象有更高的天气分类准确度.其优化方法为:最大化NWP气象和实测气象的相关度量,最小化NWP气象和实测气象的分类精度,并将其作为损失函数训练天气分类模型.上述最大化2种气象相关度量可以视为模型利用实测气象对NWP气象进行修正,而最大化分类准确度则可以视为模型利用神经网络提取与天气类型有关的气象特征. ...
基于多源气象预报总辐照度修正的光伏功率短期预测
1
2022
... 2)在实际应用中,多模态学习在语音合成、动作识别、医学图像融合、视频索引等任务的多个标准数据集上实现了最新的技术水平[26].特别是在电力领域,朱乔木[27]的研究和实验表明,相较于只考虑风速的风电功率预测,整合多种测量气象数据并挖掘其中有利于功率预测的信息,可以提高风电功率的预测精度;文献[28-29]的实验表明,相较于使用未处理的NWP数据、仅修正NWP系统误差后的数据以及传统的单点NWP修正数据,使用基于实测总辐照度修正的NWP总辐照度进行光伏功率预测的误差更小.本文提出二模态天气分类模型,其基本原理为,二模态的气象被投影到同一语义共享子空间.该子空间具有如下两方面特征:其一,子空间内的NWP气象与实测气象之间有更多的相关性;其二,子空间内NWP气象、实测气象有更高的天气分类准确度.其优化方法为:最大化NWP气象和实测气象的相关度量,最小化NWP气象和实测气象的分类精度,并将其作为损失函数训练天气分类模型.上述最大化2种气象相关度量可以视为模型利用实测气象对NWP气象进行修正,而最大化分类准确度则可以视为模型利用神经网络提取与天气类型有关的气象特征. ...
Short-term forecasting of photovoltaic power based on total irradiance correction of multi-source meteorological forecast
1
2022
... 2)在实际应用中,多模态学习在语音合成、动作识别、医学图像融合、视频索引等任务的多个标准数据集上实现了最新的技术水平[26].特别是在电力领域,朱乔木[27]的研究和实验表明,相较于只考虑风速的风电功率预测,整合多种测量气象数据并挖掘其中有利于功率预测的信息,可以提高风电功率的预测精度;文献[28-29]的实验表明,相较于使用未处理的NWP数据、仅修正NWP系统误差后的数据以及传统的单点NWP修正数据,使用基于实测总辐照度修正的NWP总辐照度进行光伏功率预测的误差更小.本文提出二模态天气分类模型,其基本原理为,二模态的气象被投影到同一语义共享子空间.该子空间具有如下两方面特征:其一,子空间内的NWP气象与实测气象之间有更多的相关性;其二,子空间内NWP气象、实测气象有更高的天气分类准确度.其优化方法为:最大化NWP气象和实测气象的相关度量,最小化NWP气象和实测气象的分类精度,并将其作为损失函数训练天气分类模型.上述最大化2种气象相关度量可以视为模型利用实测气象对NWP气象进行修正,而最大化分类准确度则可以视为模型利用神经网络提取与天气类型有关的气象特征. ...
多点数值天气预报风速和辐照度集中式修正方法研究
1
2022
... 2)在实际应用中,多模态学习在语音合成、动作识别、医学图像融合、视频索引等任务的多个标准数据集上实现了最新的技术水平[26].特别是在电力领域,朱乔木[27]的研究和实验表明,相较于只考虑风速的风电功率预测,整合多种测量气象数据并挖掘其中有利于功率预测的信息,可以提高风电功率的预测精度;文献[28-29]的实验表明,相较于使用未处理的NWP数据、仅修正NWP系统误差后的数据以及传统的单点NWP修正数据,使用基于实测总辐照度修正的NWP总辐照度进行光伏功率预测的误差更小.本文提出二模态天气分类模型,其基本原理为,二模态的气象被投影到同一语义共享子空间.该子空间具有如下两方面特征:其一,子空间内的NWP气象与实测气象之间有更多的相关性;其二,子空间内NWP气象、实测气象有更高的天气分类准确度.其优化方法为:最大化NWP气象和实测气象的相关度量,最小化NWP气象和实测气象的分类精度,并将其作为损失函数训练天气分类模型.上述最大化2种气象相关度量可以视为模型利用实测气象对NWP气象进行修正,而最大化分类准确度则可以视为模型利用神经网络提取与天气类型有关的气象特征. ...
Integrated correction method of multi-point numerical weather prediction wind speed and irradiance
1
2022
... 2)在实际应用中,多模态学习在语音合成、动作识别、医学图像融合、视频索引等任务的多个标准数据集上实现了最新的技术水平[26].特别是在电力领域,朱乔木[27]的研究和实验表明,相较于只考虑风速的风电功率预测,整合多种测量气象数据并挖掘其中有利于功率预测的信息,可以提高风电功率的预测精度;文献[28-29]的实验表明,相较于使用未处理的NWP数据、仅修正NWP系统误差后的数据以及传统的单点NWP修正数据,使用基于实测总辐照度修正的NWP总辐照度进行光伏功率预测的误差更小.本文提出二模态天气分类模型,其基本原理为,二模态的气象被投影到同一语义共享子空间.该子空间具有如下两方面特征:其一,子空间内的NWP气象与实测气象之间有更多的相关性;其二,子空间内NWP气象、实测气象有更高的天气分类准确度.其优化方法为:最大化NWP气象和实测气象的相关度量,最小化NWP气象和实测气象的分类精度,并将其作为损失函数训练天气分类模型.上述最大化2种气象相关度量可以视为模型利用实测气象对NWP气象进行修正,而最大化分类准确度则可以视为模型利用神经网络提取与天气类型有关的气象特征. ...
Distance covariance analysis
1
2017
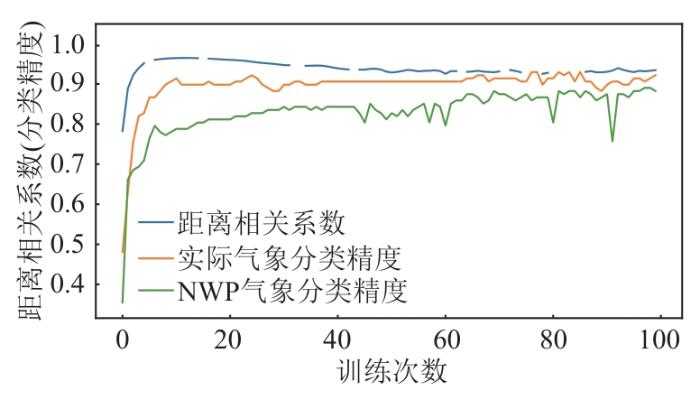
... 式中:L、L1、L2、L3分别为整体损失、二模态的距离相关损失、实际气象的分类损失、NWP气象的分类损失;为PyTorch中的交叉熵多分类损失函数;是距离相关系数,用来衡量非线性相关性,取值范围为[0,1],值越大代表2个对象越相关.因距离相关系数能以标量值衡量2组变量间的非线性相关程度,且已有简便、性质优良的样本估计表达式,较Pearson相关系数、协方差矩阵等其他相关度量有明显优势[30-31],因此本文使用文献[32]提供的距离相关样本估计表达式. ...
Independent component analysis via distance covariance
1
2017
... 式中:L、L1、L2、L3分别为整体损失、二模态的距离相关损失、实际气象的分类损失、NWP气象的分类损失;为PyTorch中的交叉熵多分类损失函数;是距离相关系数,用来衡量非线性相关性,取值范围为[0,1],值越大代表2个对象越相关.因距离相关系数能以标量值衡量2组变量间的非线性相关程度,且已有简便、性质优良的样本估计表达式,较Pearson相关系数、协方差矩阵等其他相关度量有明显优势[30-31],因此本文使用文献[32]提供的距离相关样本估计表达式. ...
Fast computing for distance covariance
1
2016
... 式中:L、L1、L2、L3分别为整体损失、二模态的距离相关损失、实际气象的分类损失、NWP气象的分类损失;为PyTorch中的交叉熵多分类损失函数;是距离相关系数,用来衡量非线性相关性,取值范围为[0,1],值越大代表2个对象越相关.因距离相关系数能以标量值衡量2组变量间的非线性相关程度,且已有简便、性质优良的样本估计表达式,较Pearson相关系数、协方差矩阵等其他相关度量有明显优势[30-31],因此本文使用文献[32]提供的距离相关样本估计表达式. ...
Modelling and simulating the spatio-temporal correlations of clustered wind power using copula
1
2013
... 对功率的概率刻画主要包含功率或预测误差的分位数、置信区间、典型场景、概率分布等,但因概率分布与随机变量相互唯一确定,且概率分布可以导出区间预测、场景等其他信息,在应用上更具优势.此外,就功率的概率建模而言,相较于直接统计或拟合功率、功率预测误差的分布,拟合功率的条件概率分布在理论上更精确[10,33].因此,本节以核密度估计[34]和Copula理论[35]为工具,建立实际功率关于预测功率的条件概率模型.此模型的输入为预测功率、实际功率,输出为实际功率关于预测功率的条件概率分布.光伏功率的条件概率建模及日前预测的具体步骤如下:首先利用本文所提的二模态天气分类模型对待预测日的天气类型进行预测;然后筛选对应天气类型的历史预测功率、实测功率数据进行条件概率建模;最后根据待预测日的预测功率,计算出完整调度时刻实际功率的条件概率密度.以待预测日为第0种天气类型为例,构建光伏功率的条件概率模型,其日前预测框架如图5所示. ...
Kernel density estimation and its application
1
2018
... 对功率的概率刻画主要包含功率或预测误差的分位数、置信区间、典型场景、概率分布等,但因概率分布与随机变量相互唯一确定,且概率分布可以导出区间预测、场景等其他信息,在应用上更具优势.此外,就功率的概率建模而言,相较于直接统计或拟合功率、功率预测误差的分布,拟合功率的条件概率分布在理论上更精确[10,33].因此,本节以核密度估计[34]和Copula理论[35]为工具,建立实际功率关于预测功率的条件概率模型.此模型的输入为预测功率、实际功率,输出为实际功率关于预测功率的条件概率分布.光伏功率的条件概率建模及日前预测的具体步骤如下:首先利用本文所提的二模态天气分类模型对待预测日的天气类型进行预测;然后筛选对应天气类型的历史预测功率、实测功率数据进行条件概率建模;最后根据待预测日的预测功率,计算出完整调度时刻实际功率的条件概率密度.以待预测日为第0种天气类型为例,构建光伏功率的条件概率模型,其日前预测框架如图5所示. ...
Copula theory:an introduction
2
2010
... 对功率的概率刻画主要包含功率或预测误差的分位数、置信区间、典型场景、概率分布等,但因概率分布与随机变量相互唯一确定,且概率分布可以导出区间预测、场景等其他信息,在应用上更具优势.此外,就功率的概率建模而言,相较于直接统计或拟合功率、功率预测误差的分布,拟合功率的条件概率分布在理论上更精确[10,33].因此,本节以核密度估计[34]和Copula理论[35]为工具,建立实际功率关于预测功率的条件概率模型.此模型的输入为预测功率、实际功率,输出为实际功率关于预测功率的条件概率分布.光伏功率的条件概率建模及日前预测的具体步骤如下:首先利用本文所提的二模态天气分类模型对待预测日的天气类型进行预测;然后筛选对应天气类型的历史预测功率、实测功率数据进行条件概率建模;最后根据待预测日的预测功率,计算出完整调度时刻实际功率的条件概率密度.以待预测日为第0种天气类型为例,构建光伏功率的条件概率模型,其日前预测框架如图5所示. ...
... 式中是函数的自变量,分别代表随机变量和的可能取值.条件概率的估计一般可分解为联合概率概率密度估计和边缘概率密度估计两部分:一方面,对于单变量概率密度估计,本文采用核密度方法,这是一种非参数估计方法,其优点是不需事先对随机变量的分布族进行假设,可直接从数据中挖掘分布信息;另一方面,使用Copula理论进行联合概率建模,是考虑到随机变量和二者具有较强的相关关系,而Copula理论提供了“通过刻画随机变量间的相依结构来对联合分布建模”的方法[35]. ...
Construction of optimal prediction intervals for load forecasting problems
1
2010
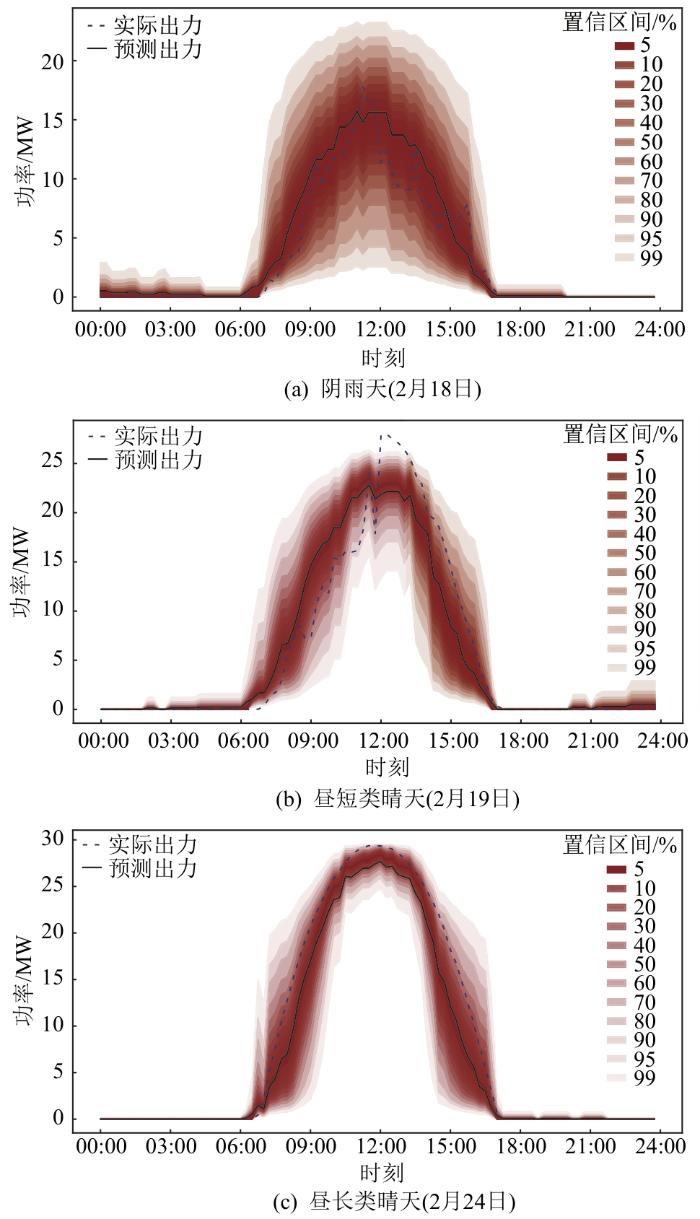
... 将预测区间覆盖率(prediction interval coverage probability,PICP)[36]、预测区间平均带宽(mean prediction interval width,MPIW)[37]作为评价指标,以此用来衡量概率预测的性能.用表示功率实际值落在预测区间内的数目,在置信水平下,其值越接近,表明建模准确度越高,模型和实际数据贴合度越高;用表示估计区间的整体宽窄情况,当置信度水平相同时,其值越小,表明预测区间越窄,模型在应用时具有更好的性能.和表达式分别如下: ...
Comprehensive review of neural network-based prediction intervals and new advances
1
2011
... 将预测区间覆盖率(prediction interval coverage probability,PICP)[36]、预测区间平均带宽(mean prediction interval width,MPIW)[37]作为评价指标,以此用来衡量概率预测的性能.用表示功率实际值落在预测区间内的数目,在置信水平下,其值越接近,表明建模准确度越高,模型和实际数据贴合度越高;用表示估计区间的整体宽窄情况,当置信度水平相同时,其值越小,表明预测区间越窄,模型在应用时具有更好的性能.和表达式分别如下: ...