基于双锁相环的海上风场综合惯量调频策略研究

doi:10.12096/j.2096-4528.pgt.22118

基于双锁相环的海上风场综合惯量调频策略研究

刘林¹, 王大龙¹, 綦晓², 周振波¹, 林焕新³, 蔡传卫³

1.南方电网南方海上风电联合开发有限公司，广东省珠海市 519070

2.暨南大学能源电力研究中心，广东省珠海市 519070

3.中国能源建设集团广东省电力设计研究院有限公司，广东省广州市 510663

Study on Double Phase-Locked Loop on the Synthetic Inertia Control of Offshore Wind Farm Frequency Regulation

LIU Lin¹, WANG Dalong¹, QI Xiao², ZHOU Zhenbo¹, LIN Huanxin³, CAI Chuanwei³

1.China Southern Power Grid Southern Offshore Wind Power Joint Development Co. , Ltd. , Zhuhai 519070, Guangdong Province, China

2.Energy and Electricity Research Center, Jinan University, Zhuhai 519070, Guangdong Province, China

3.Guangdong Electric Power Design Institute of China Energy Engineering Group Co. , Ltd. , Guangzhou 510663, Guangdong Province, China

收稿日期: 2023-05-23

基金资助:

国家自然科学基金青年项目.  52106244
广东省基础与应用基础研究基金青年项目.  2021A1515110016
中央高校基本科研业务费青年项目.  21620336.  21621042

Received: 2023-05-23

作者简介 About authors

刘林(1983)，男，工程师，研究方向为电力系统自动化、海上风电监控系统建设调试和运行，liu_lin145@163.com；

綦晓(1992)，男，博士，讲师，研究方向为高比例新能源电力系统频率控制及优化，本文通信作者，qixiao.jnu@gmail.com。

摘要

海上风电作为构建以新能源为主体的新型电力系统的重要组成部分将在沿海城市迅速发展，大规模海上风电并网将大幅削减系统惯量，降低频率抗扰能力。为此，提出基于双锁相环的海上风场综合惯量控制策略。首先，从理论上分析了锁相环对风机虚拟惯量的影响机理，探究了参数变化下风机惯量支撑能力和系统频率响应特性；其次，通过分析锁相环参数变化对风机一次调频能力的消极影响，提出基于变参数-快速双锁相环的海上风场综合惯量调频策略；最后，通过仿真验证所提调频策略的有效性。结果表明，综合惯量控制策略在频率响应快速性、抑制测量噪声等方面均具有显著优势。

关键词： 海上风场 ; 综合惯量控制 ; 调频策略 ; 新型电力系统 ; 锁相环

Abstract

To build the new power system with the main body of new energy, the offshore wind farm (OWF) is an important part and has been rapidly developed in coastal cities. However, the large-scale OWFs also reduce the inertia of power systems, which significantly decreases the anti-disturbance capability of system frequency Therefore, a synthetic inertia control strategy for OWF based on dual phase-locked loops (PLL) was proposed. First, the influence mechanism of PLL on virtual inertia of wind turbine was theoretically analyzed for variable parameter PLL. And the variation rule of wind turbine inertia support capacity and system frequency response characteristics with parameter changing PLL was explored. Then, the double PLL based OWF frequency regulation strategy was proposed through analyzing the negative effect of primary frequency regulation characteristics caused by the variable parameter of PLL. Finally, the effectiveness of the proposed frequency regulation strategy was verified though simulations. The results show that the proposed method has significant advantages in frequency response speed and frequency measurement noise suppression.

Keywords： offshore wind farm ; synthetic inertia control ; frequency regulation strategy ; new-type power system ; phase-locked loop

PDF (3055KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

刘林, 王大龙, 綦晓, 周振波, 林焕新, 蔡传卫. 基于双锁相环的海上风场综合惯量调频策略研究. 发电技术[J], 2024, 45(2): 282-290 DOI:10.12096/j.2096-4528.pgt.22118

LIU Lin, WANG Dalong, QI Xiao, ZHOU Zhenbo, LIN Huanxin, CAI Chuanwei. Study on Double Phase-Locked Loop on the Synthetic Inertia Control of Offshore Wind Farm Frequency Regulation. Power Generation Technology[J], 2024, 45(2): 282-290 DOI:10.12096/j.2096-4528.pgt.22118

0 引言

随着我国双碳目标的逐步推进，构建以新能源为主体的新型电力系统成为当前的重要发展方向^[1-3]。海上风电作为新能源的重要组成部分，与陆地风电相比，其不占用陆地资源，海上风能资源丰富，靠近城市负荷中心区，因此，更便于大规模并网和消纳，近年来受到广泛关注^[4]。然而，大规模海上风电并网将大幅降低沿海城市电网的系统惯量，严重削弱系统频率抗扰能力^[5-6]，研究如何提高海上风电主动惯量支撑能力，提升海上风电参与调频水平，具有重要的理论研究意义和工程应用价值^[7-8]。

海上风电通过电力电子器件并网，导致风电功率与电网频率解耦，无法提供传统机械惯量及频率支撑^[9]，而虚拟惯量控制下的风电机组可以模拟同步发电机惯量特性，利用风电机组储存的转子动能提供短时有功功率支撑参与频率调节^[10]，在一定程度上缓解了海上风电对城市电网频率稳定性的冲击。通过附加基于比例微分(proportional derivative，PD)虚拟惯量控制的功率控制环节^[11-14]，是提升风电机组的主动惯量支撑能力的重要方法之一。然而，PD虚拟惯量控制方法过度依赖于对系统频率微分信号的计算，而微分信号的获取往往伴随着高频噪声的放大，附加滤波器虽可在一定程度上削弱噪声的影响，但同时也降低了惯量响应速度，因此在实际应用中受限。随着对虚拟惯量理念和形式的深入研究，基于锁相环(phase-locked loop，PLL)的风电机组惯量支撑方法引起研究人员的广泛关注^[15-18]。文献[15]通过考虑锁相环动态特性，研究了直驱风电机组附加虚拟惯量控制对电力系统小干扰稳定性的影响。文献[16]分析了PLL动态过程对虚拟同步机的影响，给出了虚拟同步机及其PLL参数的整定方法。基于PLL的虚拟惯量控制方法虽然能够有效避免PD虚拟惯量控制方法微分信号获取过程中的噪声放大现象，但在利用PLL赋予风电机组惯量支撑能力的同时，也对风机一次调频施加了惯性环节，间接降低了风机一次调频响应能力。

因此，本文通过分析PLL参数对风机虚拟惯量控制响应特性的影响，以及其对一次调频响应特性的影响，提出基于变参数PLL和快速PLL的双锁相环海上风场综合惯量控制策略。该方法有效利用变参数PLL在提供虚拟惯量过程中的优势，避免PD虚拟惯量控制方法对微分噪声的放大；通过双锁相环的设计，将虚拟惯量与虚拟下垂控制环节分离，避免单一变参数PLL对下垂控制快速性的削弱，整体提高一次调频效率。

1 海上风场传统PD虚拟惯量控制模型构建

1.1 直驱永磁风机模型

海上风场通常采用直驱永磁风力发电机组，简化后二阶多机等值并网频率响应模型如图1所示。风电机组获取的机械功率^[19-20]为

P_{m} = \frac{1}{2} C_{P} ρ π r^{2} v^{3}

(1)

式中： $C_{P}$ 为风能利用系数； $ρ$ 为空气密度； $r$ 为风力机叶片半径； $v$ 为实际风速。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 海上风场等值模型

Fig. 1 Model of offshore wind farm

风电机组的机械功率通过传动系统传送到发电机上，本文的传动系统模型采用集中质块模型：

J_{w} \frac{d ω_{w}}{d t} = Δ T

(2)

式中： $J_{w}$ 为风电机组转动惯量； $ω_{w}$ 为风机转速； $Δ T$ 为电磁功率与机械功率的转矩差，表示为

Δ T = (P_{m} - P_{e}) / ω_{w}

式中 $P_{e}$ 为发电机输出的电磁功率。

在最大功率跟踪状态下，其转速和功率关系^[21-23]如下：

P_{M P P T} = k_{o p t} ω_{w}^{3}

(3)

式中 $k_{o p t}$ 为最大功率点跟踪(maximum power point tracking，MPPT)最优跟踪系数。

当风电机组参与调频时，风机将偏离最大功率跟踪点运行，但风机参考功率 $P_{r e f}$ 仍依据式(3)计算，此时记为 $P_{r e f} = k_{o p t} ω_{w}^{3}$ 。后文将统一将 $P_{M P P T}$ 记为风机功率参考值。

1.2 传统PD虚拟惯量控制下的系统频率响应模型

本文的系统频率响应模型^[10]如图2所示，主要包括火电机组模型、有功-频率动态过程及传统PD虚拟惯量控制。其中，火电机组模型包括再热锅炉模型、汽轮机模型以及发电机模型，分别如式(4)—(6)所示，由于火电机组调频模型相对成熟^[24-25]，本文不再做详细阐述。

图2

新窗口打开| 下载原图ZIP| 生成PPT

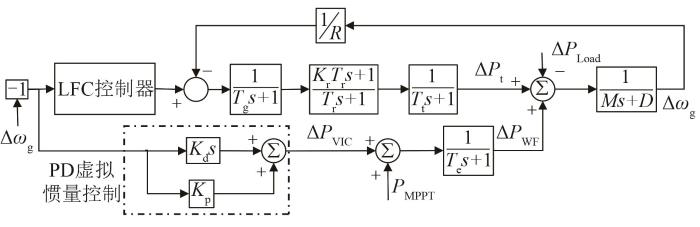
图2 传统PD虚拟惯量控制下的系统频率响应模型

Fig. 2 Frequency response model with traditional PD-based virtual inertial control

X_{g} = \frac{1}{T_{g} s + 1} \cdot u

(4)

P_{r} = \frac{K_{r} T_{r} s + 1}{T_{r} s + 1} \cdot X_{g}

(5)

P_{t} = \frac{1}{T_{t} s + 1} \cdot P_{r}

(6)

式中： $u$ 、 $X_{g}$ 和 $T_{g}$ 分别为火电厂锅炉的输入、锅炉出力及锅炉动态响应时间常数； $P_{r}$ 、 $K_{r}$ 和 $T_{r}$ 分别为火电厂汽轮机功率输出、增益系数及响应时间常数； $P_{t}$ 和 $T_{t}$ 分别为火电厂调速器功率输出及响应时间常数。

在单区域电力系统中，发电功率与负荷需求之间的不平衡将引发频率波动，该有功-频率动态过程^[26]可表示为

Δ f = \frac{1}{M s + D} (\sum Δ P_{t} + Δ P_{W F} - Δ P_{L o a d})

(7)

式中： $M$ 和 $D$ 分别为系统的惯性常数和阻尼常数； $Δ P_{t}$ 为火电厂功率变化值； $Δ P_{W F}$ 为海上风场功率变化值； $Δ P_{L o a d}$ 为电网负荷变化值。

PD虚拟惯量控制下风电机组功率变化参考值^[27]为

Δ P_{V I C} = (K_{p} + K_{d} s) Δ f

(8)

式中： $Δ f$ 为系统频率偏差； $K_{p}$ 和 $K_{d}$ 分别为PD虚拟惯量控制的比例和微分系数。

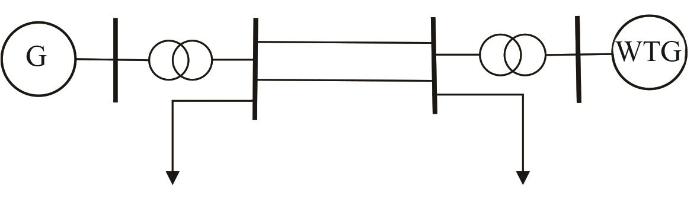
本文采用IEEE标准模型中的2机4节点模型(见图3），近似模拟桂山岛海上风场与珠海电网的连接拓扑结构，基于此进行仿真实验，验证所提控制策略的有效性。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 IEEE 2机4节点标准模型

Fig. 3 Standard model of IEEE with 2 generators and 4-buses

2 基于双锁相环的风机综合惯量控制策略

2.1 基于变参数锁相环的风机虚拟惯量控制策略

锁相环通过检测电网相位，为风机控制系统提供基准坐标。通过式(9)和式(10)可将锁相环过程进行等效转换，如图4所示。其中 $k_{p}$ 和 $k_{i}$ 是锁相环内PI控制器参数，输入信号 $θ_{0}$ 为三相电压的实际相位， $θ_{g}$ 为锁相环测量相位， $ω_{g}$ 为锁相环测量电网频率； $ω_{r e f}$ 为电网额定频率； $Δ ω_{g}$ 为频率差；V为电网三相电压。

\begin{matrix} V_{q} = V c o s (ω_{0} t) = V c o s (θ_{0}) \\ \Rightarrow 0.5 V (s i n (θ_{0} - θ_{g}) - s i n (θ_{0} + θ_{g})) = - V s i n θ_{g} \end{matrix}

(9)

式中： $ω_{0}$ 为电网实际频率； $V_{q}$ 为电网q向电压。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 基于PI的锁相环控制结构框图

Fig. 4 Control structure of PI-based PLL

此时，锁相环的线性闭环传递函数可推导如下：

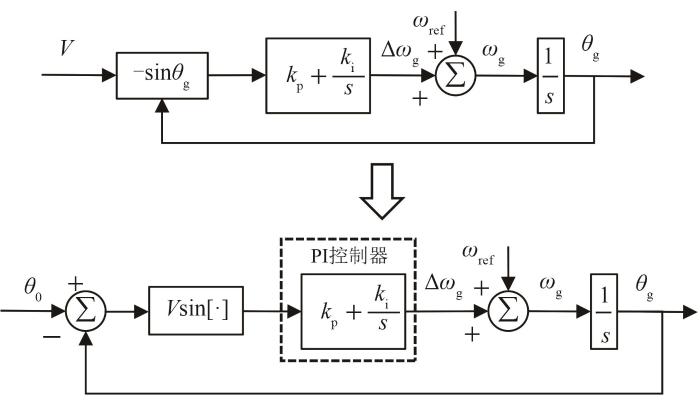
\frac{Δ θ_{g}}{Δ θ_{0}} = G_{P L L} (s) \approx \frac{K_{p} s + K_{i}}{s^{2} + K_{p} s + K_{i}}

(10)

为研究锁相环对风机虚拟惯量及其对功率控制的影响，本文采用线性化风机控制系统，如图5所示。其中 $Δ T_{e}$ 和 $Δ T_{m}$ 分别为电磁转矩变化值和机械转矩变化值； $Δ ω_{g}$ 和 $Δ ω_{r e f}$ 分别为风机转速变化值及其参考值； $Δ θ$ 、 $Δ θ_{g}$ 和 $Δ θ_{p}$ 分别为相位偏差值、电网实际相位偏差值及锁相环测量相位偏差值； $x_{a d}$ 和 $K_{e q}$ 分别为互阻抗和等效增益系数。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 线性化后的风机控制系统结构图

Fig. 5 Control structure of linearized control system of wind turbine

为明晰锁相环控制环节在风机虚拟惯量控制过程中与功率之间的关系，可通过转矩差 $Δ T$ 、转速差 $Δ ω$ 、功率差 $Δ P$ 与内电势 $Δ E$ 、相位差 $Δ θ$ 之间的等效变换，建立相位-功率方程，如式(11)所示，同时，可得出风机等效惯量及阻尼，分别如式(12)、(13)所示。由于篇幅所限，本文不再对理论推导详细展开，具体步骤可参考文献[27-28]。

Δ θ_{g} = - \frac{1}{K} Δ P + Δ θ

(11)

M_{e q} = \frac{ω_{w} J_{w}}{k_{i v} x_{a d} K}

(12)

D_{e q} = \frac{k_{i p}}{k_{i v} x_{a d} K}

(13)

式中： $M_{e q}$ 为有功功率控制环的惯性响应时间常数，近似为1； $D_{e q}$ 是等效下垂系数，近似为0.6；K为等效变换系数； $k_{i p}$ 为比例控制系数，取3； $k_{i v}$ 为积分控制系数，取6。

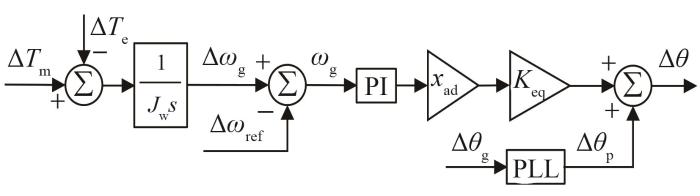
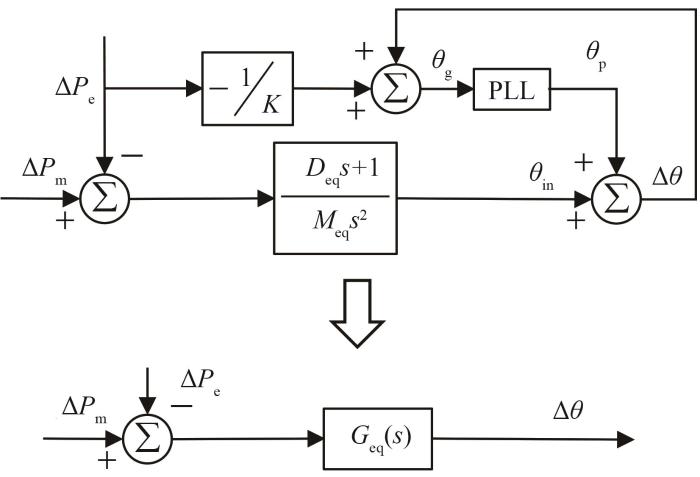
此时，可构建基于变参数锁相环的等效风机控制框图，如图6所示，进一步推导其等效传递函数如式(14)所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 基于变参数锁相环的等效风机控制框图

Fig. 6 Equivalent control structure of variable parameter PLL-based wind turbine

\begin{matrix} G_{e q} (s) = (\frac{D_{e q}}{M_{e q}} + \frac{K_{p}}{K}) + (\frac{1}{M_{e q}} + \frac{K_{i}}{K} + \frac{K_{p} D}{M_{e q}}) \cdot \frac{1}{s} \\ + \frac{K_{p} + D_{e q} K_{i}}{M_{e q} s^{2}} + \frac{K_{i}}{M_{e q} s^{3}} \end{matrix}

(14)

该过程的等效惯量如式(15)所示。

\begin{matrix} M (s) = (\frac{1}{M_{e q}} + \frac{K_{i}}{K} + \frac{K_{p} D}{M_{e q}}) + \\ \frac{K_{p} + D_{e q} K_{i}}{M_{e q} s} + \frac{K_{i}}{M_{e q} s^{2}} \end{matrix}

(15)

由式(15)可知，锁相环控制器参数可通过改变风机内电势惯量，进而改变风机输出功率，从而达到虚拟惯量控制的效果。

2.2 双锁相环风机综合惯量控制策略理论分析

在变参数锁相环控制下，对式(14)系统进行频域性能分析，研究变参数锁相环对频率测量快速性的影响。令k_i=0.14，使k_p从2逐渐增大至64，其伯德图如图7所示，可以发现，随着k_p的增大，系统截止频率逐渐增大。因此，系统响应快速性与锁相环控制参数k_p具有正相关性。同样地，令k_p=6，使k_i从0.014逐渐增大至1 400，其伯德图如图8所示，可以发现，随着k_i的增大，系统截止频率逐渐增大。因此，系统响应快速性与锁相环控制参数k_i同样具有正相关性。

图7

新窗口打开| 下载原图ZIP| 生成PPT

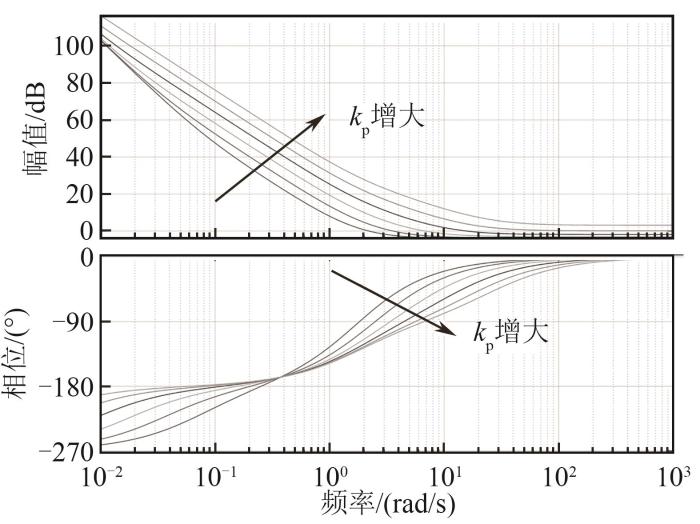
图7 变参数锁相环伯德图(k_i不变，k_p增大)

Fig. 7 Bode diagram of variable parameter PLL with certain k_iand variable k_p

图8

新窗口打开| 下载原图ZIP| 生成PPT

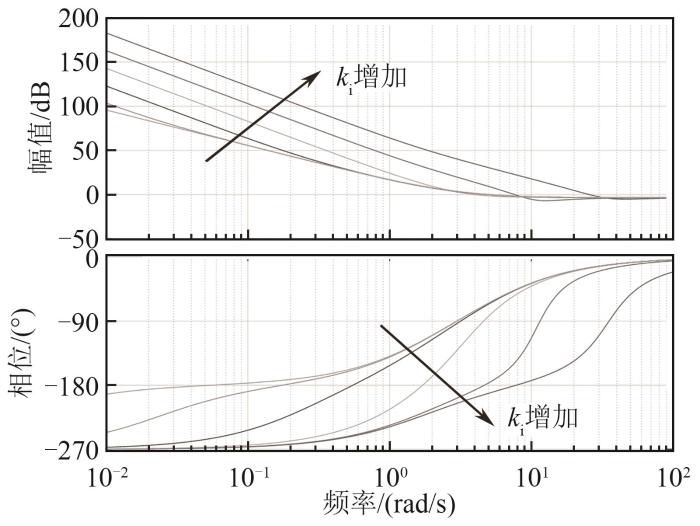
图8 变参数锁相环伯德图(k_p不变，k_i增大)

Fig. 8 Bode diagram of variable parameter PLL with certain k_p and variable k_i

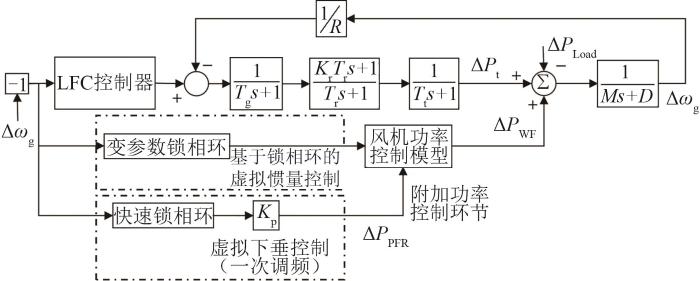
经上述分析可得，在采用变参数锁相环提供风机虚拟惯量的同时，导致系统频率测量过程产生一定程度的惯性，该惯性不利于实现风机虚拟下垂控制。因此，本文提出基于快速锁相环的风机虚拟下垂控制策略，以避免变参数锁相环下频率测量延迟对风机一次调频响应特性的影响，进而构建基于变参数-快速双锁相环的风机综合惯量控制策略，利用快速锁相环检测系统频率信号，将其传送至风电机组一次调频控制器，变参数锁相环通过检测系统相位信号，实现风电机组对系统频率的惯量支撑，二者之间相互独立，各自测量所需信号。基于双锁相环的风机综合惯量控制策略结构如图9所示。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 基于双锁相环的风机综合惯量调频策略

Fig. 9 Equivalent control structure of PLL-based wind turbine

其中，快速锁相环的PI控制器参数选取原则为：k_p与k_i参数调大，以保证频率测量的快速性。变参数锁相环的PI控制器参数选取原则为：依据所需提供的虚拟惯量大小进行调节，其相关性将通过仿真分析得出。

3 仿真结果与分析

为分析变参数锁相环中k_p和k_i参数变化对风机虚拟惯量响应的影响并验证所提出的双锁相环控制策略的有效性，本文硬件设备是基于暨南大学高性能计算中心(Windows Server 2019服务器系统，CPU为Intel Xeon Cascade Lake 8255C，32核心，128G内存)，结合图7所示的控制逻辑及IEEE 2机4节点标准模型，在MATLAB 2018b/Simulink环境下进行仿真实验。

3.1 变参数锁相环下风机虚拟惯量响应特性分析

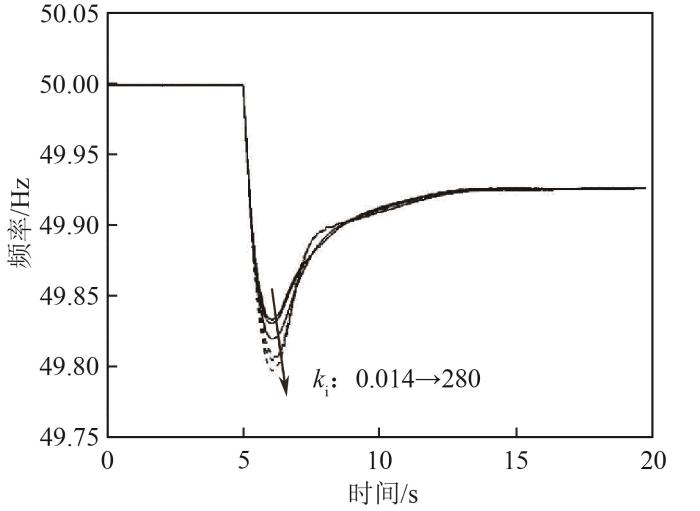
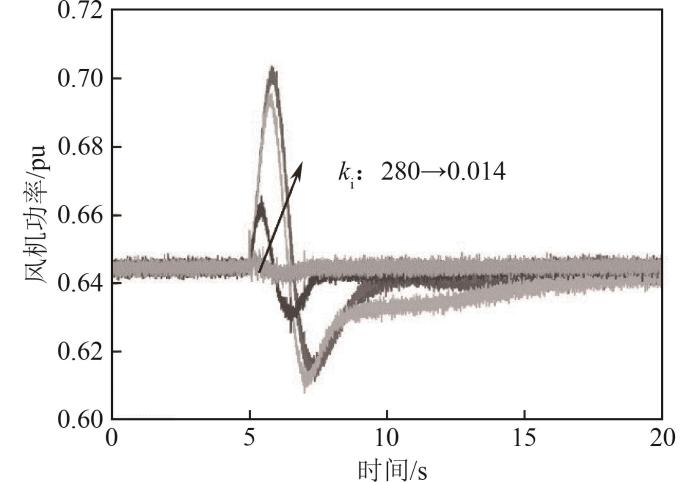
保持风速为10 m/s，令负荷在5 s处发生0.1 pu的阶跃扰动，分析参数不同时，风机虚拟惯量响应特性的变化。令锁相环控制器积分系数k_i分别为0.014、0.14、1.4、14、140、280，逐渐增大，图10为k_i变化下系统频率响应曲线。当k_i为0.014时，频率响应超调量最小，频率最低点为49.832 Hz，随着k_i增大，频率响应超调逐渐增大；当k_i为280时，频率最低点为49.796 Hz。图11为锁相环参数k_i变化下风机功率响应曲线，当k_i为0.014时，风机功率响应峰值最高，为0.703 pu，随着k_i增大，风机功率响应峰值减小，当k_i为280时，风机功率响应峰值最低，为0.647 pu。实验结果表明，k_i越大，频率响应超调越大，但频率变化速度越快，风机参与调频出力越少。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 锁相环参数k_i变化下系统频率响应曲线

Fig. 10 Curves of system frequency responses with variation of PLL parameter k_i

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 锁相环参数k_i变化下风机功率响应曲线

Fig. 11 Curves of wind turbine power responses with variation of PLL parameter k_i

令锁相环控制器比例系数k_p分别为2、4、8、16、32、64，逐渐增大，图12为k_p变化下系统频率响应曲线，k_p为2时，频率最低点为49.848 Hz，k_p为64时，频率最低点为49.811 Hz。可以发现，随着k_p增大，系统频率最大偏差逐渐增大，且频率变化速度逐渐加快。图13为锁相环参数k_p变化下风机功率响应曲线，当k_p为2时，风机功率响应峰值最高，为0.756 pu，随着k_p增大，风机功率响应峰值减小；当k_p为64时，风机功率响应峰值降至最低，为0.653 pu。实验结果表明，k_p越小，频率响应超调越小，风机调频出力越多，频率变化速度越慢。

图12

新窗口打开| 下载原图ZIP| 生成PPT

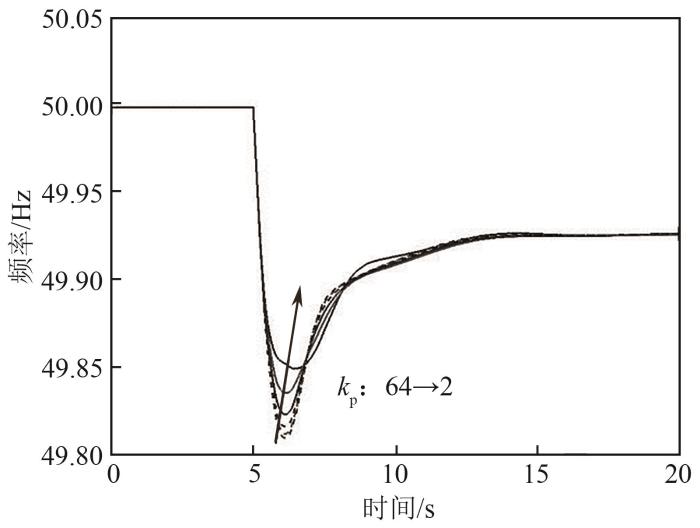
图12 锁相环参数k_p变化下系统频率响应曲线

Fig. 12 Curves of system frequency responses with variation of PLL parameter k_p

图13

新窗口打开| 下载原图ZIP| 生成PPT

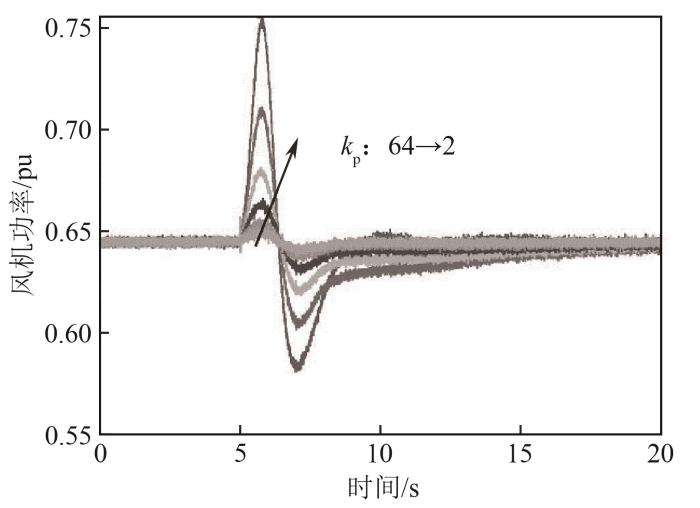
图13 锁相环参数k_p变化下风机功率响应曲线

Fig. 13 Curves of wind turbine power responses with variation of PLL parameter k_p

3.2 双锁相环下风机综合惯量响应特性分析

同样地，令风速为10 m/s，负荷在5 s处发生0.1 pu的阶跃扰动，分别对传统单锁相环控制策略和本文所提变参数双锁相环控制策略进行仿真。如图14所示，本文双锁相环控制策略下系统频率响应的频率最低点为49.856 Hz，传统单锁相环控制策略下的系统频率响应最低点为49.837 Hz，且本文所提策略比传统单锁相环控制策略系统频率响应更快，能够快速达到稳定频率。如图15所示，2种策略风机功率响应曲线几乎重合，表明双锁相环控制策略相比单锁相环控制策略能在不影响风机调频出力的情况下，优化最大系统频率偏差，同时提升系统频率响应快速性。

图14

新窗口打开| 下载原图ZIP| 生成PPT

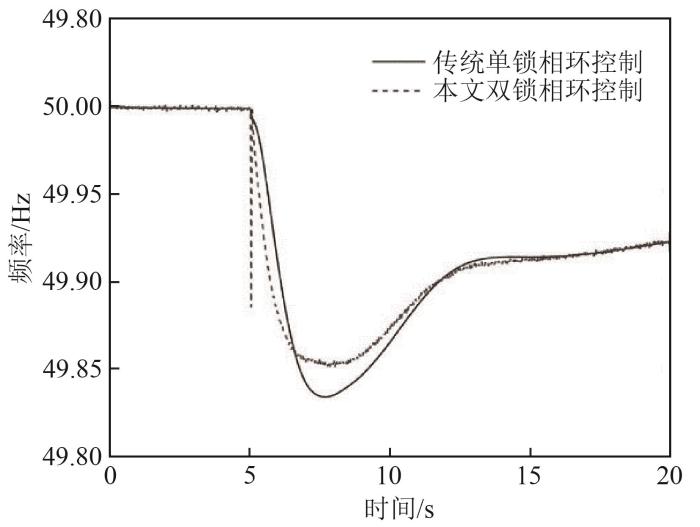
图14 不同锁相环控制策略下系统频率响应曲线

Fig. 14 Curves of system frequency responses with different PLL control strategies

图15

新窗口打开| 下载原图ZIP| 生成PPT

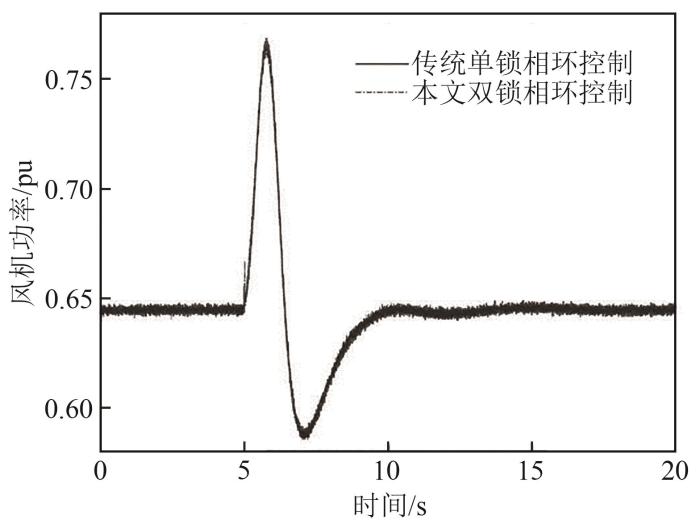
图15 不同锁相环控制策略下风机功率响应曲线

Fig. 15 Curves of wind turbine power responses with different PLL control strategies

3.3 不同控制策略对频率测量噪声的抗扰性分析

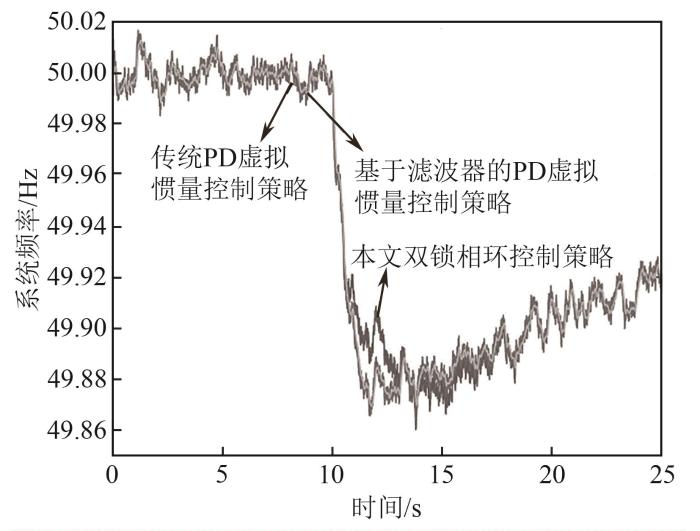
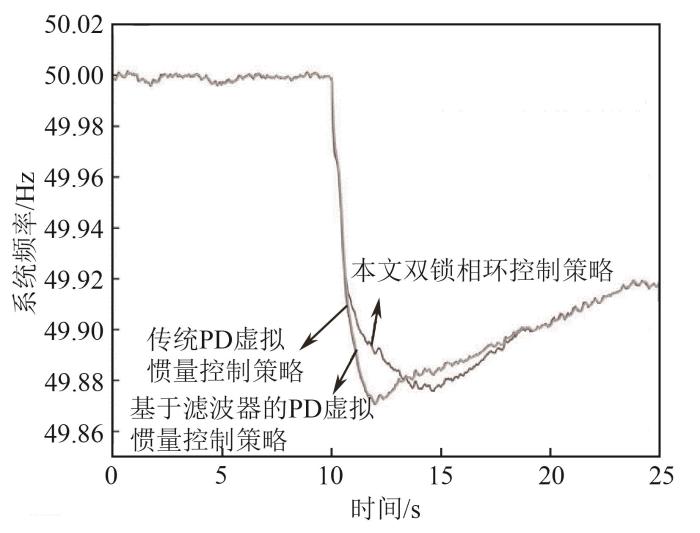
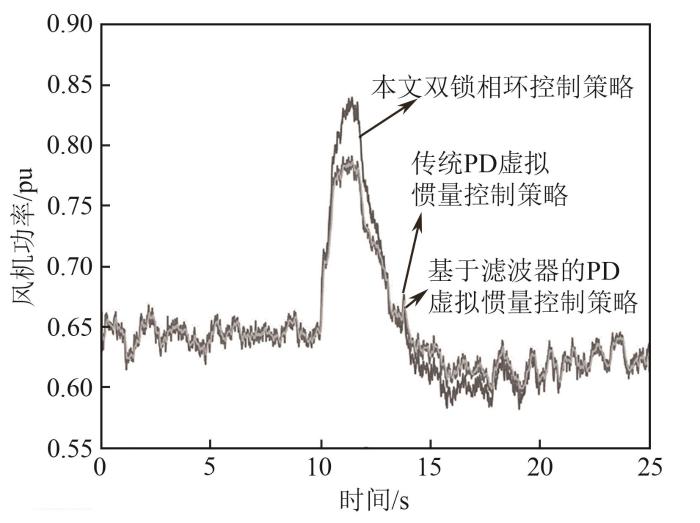
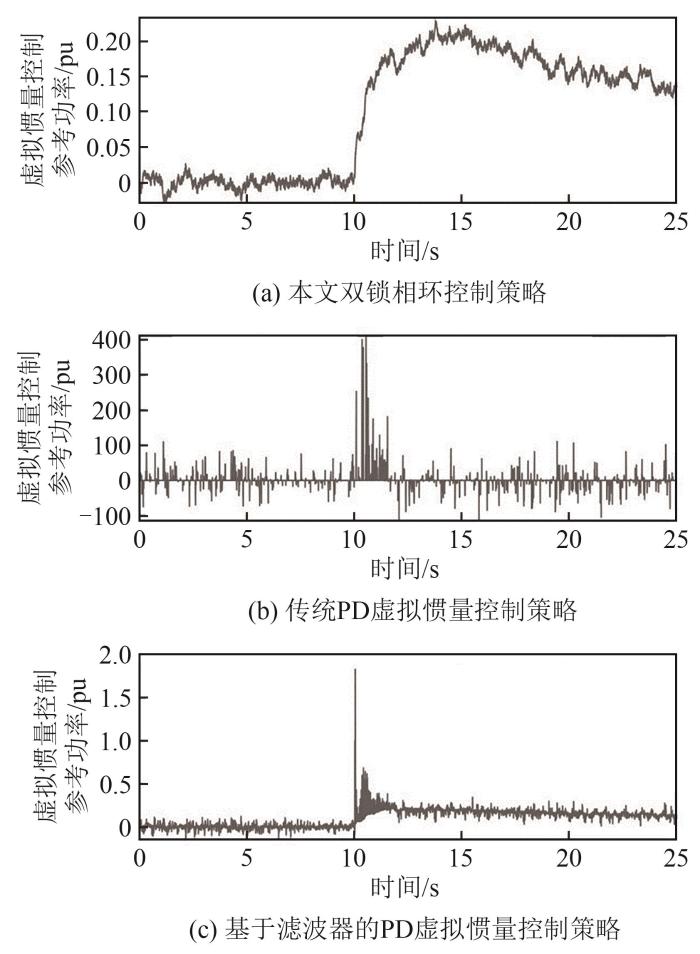
在负荷产生0.1 pu阶跃扰动下，同时考虑测量噪声作用的情况，分别对传统PD虚拟惯量控制策略、基于滤波器的PD虚拟惯量控制策略，以及本文所提双锁相环控制策略进行仿真实验，结果如图16—19所示。其中，图16为不同控制策略下的系统测量频率，图17为不同控制策略下的系统实际频率，对比可以发现，本文所提双锁相环控制策略能够提供更快速的惯量支撑。图18为不同控制策略下的风机功率响应曲线，图19为虚拟惯量控制器所产生的风机功率变化参考值，结合以上两图结果可知，传统PD虚拟惯量控制策略极大程度上放大了测量噪声，导致风机功率参考信号大幅变化，远超本文所提双锁相环控制策略的0.2 pu范围，即使在滤波器作用下，该值仍具有较大变化幅值，尤其是在发生系统功率不平衡扰动后。

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16 不同控制策略下的系统测量频率响应曲线

Fig. 16 Curves of power system measurement frequency responses with different control strategies

图17

新窗口打开| 下载原图ZIP| 生成PPT

图17 不同控制策略下的系统实际频率响应曲线

Fig. 17 Curves of power system actual frequency responses with different control strategies

图18

新窗口打开| 下载原图ZIP| 生成PPT

图18 不同控制策略下风机功率响应曲线

Fig. 18 Curves of wind power response with different control strategies

图19

新窗口打开| 下载原图ZIP| 生成PPT

图19 不同控制策略下风机功率变化参考值曲线

Fig. 19 Curves of referenced wind power change with different control strategies

4 结论

从锁相环控制过程出发，研究锁相环参数变化对风机虚拟惯量及一次调频过程的影响，提出了基于双锁相环的海上风场综合惯量控制策略，具体结论如下：

1）该方法有效避免了传统PD虚拟惯量控制方法对频率测量噪声的放大影响；

2）与基于滤波器的PD虚拟惯量控制方法以及基于单锁相环的虚拟惯量控制方法相比，该方法可有效提高虚拟下垂控制响应快速性，优化综合惯量支撑水平；

3）可进一步结合实际系统对海上风场惯量支撑水平的需求，量化锁相环参数与风场虚拟惯量的数学描述，根据系统不同运行工况，动态调控双锁相环控制下的风场惯量支撑水平，在确保电网频率稳定性的同时，提高风场运行经济性。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

VEERS

， DYKES

， LANTZ

，et al ．

Grand challenges in the science of wind energy

[J]．Science，2019，366：6464．