基于Logistic快速最小误差熵算法的配电变压器停电预测

doi:10.12096/j.2096-4528.pgt.21006

基于Logistic快速最小误差熵算法的配电变压器停电预测

许中¹, 栾乐¹, 莫文雄¹, 罗思敏¹, 叶宗林², 陈超², 赖轩达², 解明辉²

1.广东电网有限责任公司广州供电局, 广东省广州市 510000

2.西安交通大学电气工程学院, 陕西省西安市 710049

Distribution Transformer Outage Prediction Based on Logistic Fast Minimum Error Entropy Algorithm

XU Zhong¹, LUAN Le¹, MO Wenxiong¹, LUO Simin¹, YE Zonglin², CHEN Chao², LAI Xuanda², XIE Minghui²

1.Guangzhou Power Supply, Guangdong Power Grid Co. , Ltd. , Guangzhou 510000, Guangdong Province, China

2.School of Electrical Engineering, Xi’an Jiaotong University, Xi’an 710049, Shaanxi Province, China

收稿日期: 2021-06-30

基金资助:

中国南方电网责任有限公司科技项目. GZHKJXM20180068

Received: 2021-06-30

作者简介 About authors

许中(1986)，男，硕士，高级工程师，主要研究方向为电能质量，348867958@qq.com；

栾乐(1982)，女，硕士，高级工程师，主要研究方向为设备状态评价，149529958@qq.com；

莫文雄(1971)，男，硕士，教授级高级工程师，主要研究方向为电气工程，gzmwx@139.com；

罗思敏(1988)，男，硕士，高级工程师，主要研究方向为智能配电网，本文通信作者，rushlsm@163.com；

叶宗林(1990)，男，博士，主要研究方向为数据挖掘、过程控制和工业自动化，yezonglin1990@gmail.com；

陈超(1995)，男，硕士研究生，主要研究方向为配电网大数据分析与态势感知研究，610825983@qq.com；

赖轩达(1999)，男，硕士研究生，主要研究方向为电力大数据，lxd593@stu.xjtu.edu.cn；

解明辉(1998)，男，硕士研究生，主要研究方向为电力大数据，619425976@qq.com。

摘要

为了提高配电变压器停电预测的速度和准确性，提出了一种基于Logistic快速最小误差熵算法的配变停电预测方法。在最小熵回归算法的基础上，提出了快速最小误差熵算法，基本保持了最小熵回归的回归效果，并且显著地减少了算法的运行时间；针对配变停电预测适用Logistic回归的情况，提出了基于Logistic的快速最小误差熵回归算法，选取配电变压器重过载时长、最大有功负载率、平均有功负载率、平均三相不平衡度以及重三相不平衡度作为配变停电预测的特征变量数据，建立了配电变压器停电预测模型，实验预测结果优于Logistic回归。

关键词： Logistic快速最小误差熵 ; 配电变压器 ; 停电预测

Abstract

In order to improve the speed and accuracy of distribution transformer outage prediction, a distribution transformer outage prediction method based on Logistic fast minimum error entropy algorithm was proposed. Aiming at the problem that the basic minimum entropy regression algorithm runs too slowly, a fast minimum error entropy algorithm was proposed, which can keep the same regression effect as the minimum entropy regression, and greatly reduce the running time of the algorithm. In view of the application of Logistic regression in outage prediction, a fast minimum error entropy regression algorithm based on logistic was proposed, and the weight of distribution transformer was selected. The overload duration, maximum active load rate, average active load rate, average three-phase unbalance degree and heavy three-phase unbalance degree were used as the characteristic variable data of distribution transformer outage prediction. A distribution transformer outage prediction model was established, and the effect was found to be better than Logistic regression in the comparative experiment.

Keywords： Logistic fast minimum error entropy ; distribution transformer ; outage prediction

PDF (1635KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

许中, 栾乐, 莫文雄, 罗思敏, 叶宗林, 陈超, 赖轩达, 解明辉. 基于Logistic快速最小误差熵算法的配电变压器停电预测. 发电技术[J], 2022, 43(2): 313-319 DOI:10.12096/j.2096-4528.pgt.21006

XU Zhong, LUAN Le, MO Wenxiong, LUO Simin, YE Zonglin, CHEN Chao, LAI Xuanda, XIE Minghui. Distribution Transformer Outage Prediction Based on Logistic Fast Minimum Error Entropy Algorithm. Power Generation Technology[J], 2022, 43(2): 313-319 DOI:10.12096/j.2096-4528.pgt.21006

0 引言

配电网是指从输电网或地区发电厂接受电能，通过配电设施就地分配或按电压逐级分配给各类用户的电力网^[1]。近年来，随着我国经济的快速发展，电力负荷的增长明显加快，对城市配电网的供电能力、电能质量、供电可靠性都有了更高的要求^[2-5]。配电网作为与用户直接相连的电力网，不仅规模庞大、设备繁多，且供电环境复杂，据统计，80%以上的停电事故由配电网故障引起^[6]。因此，研究一种精确、高效的配电变压器停电预测方法具有重要的实际意义。

目前配电网停电预测方法的研究主要集中在配电网可靠性评估^[7-12]和基于大数据技术的配电网停电预测方面。文献[13]分析了配电网故障数据之间的关联性，并基于Logistic分类算法建立故障识别模型进行停电预测。文献[14]针对极端天气下配电网停电问题，利用历史灾损记录和灾害数值模拟数据，构建灾害时间贝叶斯网络模型进行停电预测。文献[15]针对台风灾害，综合考虑气象、电网及地理因素，提出一种基于随机森林算法的用户停电区域预测评估方法。文献[16]针对超高温、暴雨等恶劣天气条件，采用XGBoost算法建立了线路停电数量预测模型。文献[17]提出建立贝叶斯网络预测飓风情况下的配电网停电概率。文献[18]考虑配电网下面的植被情况和雷达检测数据，通过建立随机森林模型来提高停电预测结果的准确性。

本文将基于配变运行数据得到的停电预测特征之外的因素作为误差因素，采用最小误差熵估计^[19]。针对基本的最小熵回归算法运行时间较长的问题，提出了快速最小误差熵算法；然后针对停电预测适用Logistic回归的情况，提出了基于Logistic的快速最小误差熵回归算法，建立了配电网变压器特征变量数据的配网停电预测模型，以实际数据为例验证了所提方法的有效性。

1 传统最小误差熵算法

最小误差熵算法通过最小化回归算法中误差所包含的信息量从而使得回归模型所包含的信息量最大化。最小误差熵算法采用二阶Renyi熵^[20]来表示模型误差中所包含的信息量：

H (E) = - l o g E_{P} (p_{E}) = - l o g \int p_{E}^{2} (e) d e

(1)

式中：E为回归误差的随机变量； $H (E$ $)$ 为E的熵； $p_{E} (e)$ 为E的概率密度函数；e为设定的概率密度函数自变量取值； $E_{P} (\cdot)$ 为对应随机变量的期望。利用Parzen窗方法^[21]，E的概率密度函数 ${\hat{p}}_{E} (e)$ 可以表示为

{\hat{p}}_{E} (e) = \frac{1}{n} \sum_{i = 1}^{n} K_{h} (e - e_{i})

(2)

式中：n为随机变量E的采样样本数；K为核函数； $e_{i}$ 为样本值；h为带宽。一般情况下，选择高斯核函数作为核函数，即 $K_{h} (z) = \frac{2}{\sqrt[]{2 π} h} e x p (- \frac{z^{2}}{2 h^{2}})$ 。则随机变量的信息熵的估计量 $\hat{H} (f)$ 为

\hat{H} (f) = - l o g \frac{1}{n^{2}} \sum_{i = 1}^{n} \sum_{j = 1}^{n} K_{h} (e_{i} - e_{j})

(3)

由于对数函数单调递增，实际应用中，最小化 $\hat{H} (f)$ 时可以将其移除而不影响最小化的结果。故变换后的随机变量对应的信息熵的估计量为

\hat{H} (f) = - \frac{1}{n^{2}} \sum_{i = 1}^{n} \sum_{j = 1}^{n} K_{h} (e_{i} - e_{j})

(4)

对于线性回归模型， $y = w^{T} x + e$ 需要从数据样本中估计出 w。由于 $e_{i} = y_{i} - w^{T} x_{i}$ ，则对应的变换后的误差信息熵的估计量为关于 w 的函数：

\hat{R} (w) = - \frac{1}{n^{2}} \sum_{i = 1}^{n} \sum_{j = 1}^{n} K_{h} [(y_{i} - w^{T} x_{i}) - (y_{j} - w^{T} x_{j})]

(5)

估计量 $\hat{R} (w)$ 可以通过用梯度下降法极小化式(5)来求解。由于式(5)中含有二重求和运算，最小误差熵算法的时间复杂度为 $O (n^{2})$ ，这就使得随着样本数目的增大，最小误差熵算法所需要的时间会快速增加。

2 Logistic快速最小误差熵算法

在对配电网变压器的停电状况进行预测时，由于在训练样本中，配变的预测结果为“停电”与“不停电”2种情况，即预测结果为布尔变量，而一般的回归模型的预测结果是连续变量，因此需要建立起这2种不同变量类型间的联系，将区间 $(- \infty, + \infty)$ 的结果映射到[0,1]。Sigmod函数非常适合实现这一点，对应的算法即为Logistic回归。

Logistic回归通过Sigmod函数，在线性回归的基础上，将线性模型在区间 $(- \infty, + \infty)$ 的预测结果映射到[0,1]。由于一个事件的概率值恰好在[0,1]，故Sigmod函数的预测结果具有概率上的意义，预测值可以代表一个事件发生的概率，当预测概率小于0.5时，分类结果为负类，即表示不停电；当预测概率大于0.5时，分类结果为正类，表示停电。因此，在配变停电故障的预测过程中，Logistic回归可以建立配电网变压器的各种特征参数与其停电概率之间的关系。

2.1 Logistic回归

常用的二项Logistic回归模型为以下条件概率分布：

P (Y = 1 | x) = \frac{1}{1 + e x p [- (w^{T} x + b)]} = \frac{e x p (w^{T} x + b)}{1 + e x p (w^{T} x + b)}

(6)

P (Y = 0 | x) = 1 - P (Y = 1 | x) = \frac{1}{1 + e x p (w^{T} x + b)}

(7)

式中： $x \in R_{n}$ 是模型输入；n为模型输入的维数；Y=1和Y=0是Y的2个可能取值； $P (Y = 1 | x)$ 和

$P (Y = 0 | x)$ 分别为Y取得这2个可能取值的概率； $w \in R_{n}$ 和 $b \in R_{n}$ 是参数， w 为权值向量，b为偏置。为了表达方便，可以将权值向量和输入向量进行扩充，即 $w = (w^{(1)}, w^{(2)}, \dots, w^{(n)} {, b)}^{T}$ ， $x = (x^{(1)}, x^{(2)}, \dots, x^{(n)} {, 1)}^{T}$ 。

2.2 快速最小误差熵

一个随机变量X的微分熵^[22]如式(8)所示：

H (x) = - \int p (x) l o g p (x) d x

(8)

假设一个随机变量x接近与其均值和方差相同的高斯分布，将其概率密度函数GramCharlier展开式^[23]代入式(8)，化简后可得：

H (x) \approx \frac{1}{2} l o g 2 π e σ - \frac{k_{3}^{2} (x)}{12 σ^{5}} - \frac{k_{4}^{2} (x)}{48 σ^{7}}

(9)

式中： $σ$ 为随机变量x的方差； $k_{3} (x)$ 和 $k_{4} (x)$ 分别为x的三阶和四阶累积量，即偏度和峭度。

对于线性回归模型，其误差的熵为

\begin{matrix} H (e_{w}) \approx \frac{1}{2} l o g 2 π e + \frac{1}{2} l o g σ (e_{w}) - \\ \frac{k_{3}^{2} (e_{w})}{12 σ^{5} (e_{w})} - \frac{k_{4}^{2} (e_{w})}{48 σ^{7} (e_{w})} \end{matrix}

(10)

2.3 Logistic快速最小误差熵回归算法

参考线性回归与Logistic回归的转换，快速最小误差熵回归的配电网变压器停电概率预测结果也为连续变量，因此也需要叠加一个Sigmod函数，将配电变压器的各种特征参数映射到[0, 1]，称为Logistic快速最小误差熵算法。则对于模型：

y = \frac{1}{1 + e x p (- w^{T} x)}

(11)

Logistic快速最小误差熵算法的误差可以表示为

e_{i} = y_{i} - \frac{1}{1 + e x p (- w^{T} x_{i})}

(12)

在得到式(10)的过程中，线性回归的误差被作为一个随机变量进行推导，并没有使用关于线性回归的信息。因此，式(10)的表达式与回归算法的形式没有关系。故Logistic快速最小误差熵算法误差的熵与线性回归误差的熵的表达式(10)相同。

为了求出 $H (e_{w})$ 的最小值， $H (e_{w}$ )关于 w 的导数为

\begin{matrix} \frac{\partial H (e_{w})}{\partial w} = \frac{1}{2 σ (e_{w}) l n 2} \frac{\partial σ (e_{w})}{\partial w} - \frac{1}{6 σ^{6} (e_{w})} \times \\ [σ (e_{w}) k_{3} (e_{w}) \frac{\partial k_{3} (e_{w})}{\partial w} - \\ 2 k_{3}^{2} (e_{w}) \frac{\partial σ (e_{w})}{\partial w}] - \frac{1}{8 σ^{7} (e_{w})} \times \\ [16 σ (e_{w}) k_{4} (e_{w}) \frac{\partial k_{4} (e_{w})}{\partial w} - k_{4}^{2} (e_{w}) \frac{\partial σ (e_{w})}{\partial w}] \end{matrix}

(13)

其中：

σ (e_{w}) = \sqrt[]{E_{p} (E_{w}^{2}) - [E_{p} (E_{w} {)]}^{2}}

(14)

\begin{matrix} \frac{\partial σ (e_{w})}{\partial w} = \frac{1}{2 \sqrt[]{E_{P} (E_{w}^{2}) - [E_{P} (E_{w} {)]}^{2}}} \times \\ [\frac{\partial E_{P} [E_{w}^{2}]}{\partial w} - \frac{\partial [E_{P} (E_{w} {)]}^{2}}{\partial w}] \end{matrix}

(15)

\begin{matrix} k_{3} (e_{w}) = \frac{1}{n} \sum_{i = 1}^{n} [y_{i}^{3} - 3 y_{i}^{2} S i g (w) - \\ 3 y_{i} S i g^{2} (w) + S i g^{3} (w)] \end{matrix}

(16)

\begin{matrix} \frac{\partial k_{3} (e_{w})}{\partial w} = \frac{1}{n} \sum_{i = 1}^{n} {[- 3 y_{i}^{2} S i g^{2} (w) - 6 y_{i} S i g^{3} (w) + \\ 3 S i g^{4} (w)] x_{i} e x p (- w^{T} x_{i})]} \end{matrix}

(17)

\begin{matrix} k_{4} (e_{w}) = \frac{1}{n} \sum_{i = 1}^{n} [y_{i}^{4} - 4 y_{i}^{3} S i g (w) + 6 y_{i}^{2} S i g^{2} (w) - \\ 4 y_{i} S i g^{3} (w) + S i g^{4} (w)] - 3 \end{matrix}

(18)

\begin{matrix} \frac{\partial k_{4} (e_{w})}{\partial w} = \frac{1}{n} \sum_{i = 1}^{n} {[- 4 y_{i}^{3} S i g^{2} (w) + 12 y_{i}^{2} S i g^{3} (w) - \\ 12 y_{i} S i g^{4} (w) + 4 S i g^{5} (w)] \times x_{i} e x p (- w^{T} x_{i})} \end{matrix}

(19)

为了获得能够最小化 $H (e_{w})$ 的 w，使用如下所示的梯度下降迭代格式：

{\hat{w}}_{k + 1} = {\hat{w}}_{k} - α \frac{\partial H (e_{w_{k}})}{\partial {\hat{w}}_{k}}

(20)

式中： ${\hat{w}}_{k}$ 和 ${\hat{w}}_{k + 1}$ 分别表示第k次和k+1次迭代得到的线性回归系数向量；α表示迭代步长，由Arimijo准则确定。

由于这些式子的计算复杂度均为O(n)，故快速最小误差熵算法的计算复杂度也为O(n)。因此理论上可以认为快速最小误差熵算法的运算速度快于传统的最小误差熵算法。

3 案例分析

3.1 算法时间复杂度验证

本文通过实验比较快速最小误差熵算法与最小误差熵算法的程序运行时间消耗。设线性回归模型 $y = {w_{*}}^{T} x + e$ ，其中模型参数取 $x ~ N (0, I_{10})$ ， $w_{*} = {[1 - 1 1 - 1 1 - 1 1 - 1 1 - 1]}^{T}$ 。其中，噪声信号采用高斯噪声 $e ~ N (0,1)$ ，快速最小误差熵算法的迭代歩长取 $α = \sqrt[]{0.005 π}$ ，最小误差熵算法高斯核的核函数参数取h=10^[24]。实验中采用从100到500的样本数量。算法时间复杂度验证时，取90%的样本作为训练集，10%的样本作为验证集。实验结果如表1所示。

表1 2种算法对于高斯误差的运行时间

Tab. 1 Running time of two algorithms for Gaussian error

样本数量	平均运行时间/s		最快运行时间/s
样本数量	最小误差熵	快速最小误差熵	最小误差熵	快速最小误差熵
100	103.89	0.040 1	77.77	0.015 6
200	384.31	0.058 0	310.05	0.031 2
300	801.52	0.076 9	654.21	0.046 8
400	1 430.61	0.100 0	1 254.12	0.046 8
500	2 306.24	0.110 4	2 072.50	0.062 4

新窗口打开| 下载CSV

从表1中可以看到，在算法平均运行时间和最快运行时间2方面，快速最小误差熵算法均比最小误差熵算法耗时少。

3.2 配电网停电预测算法验证

考虑配网中与停电相关的因素以及实际可获取运行数据，本文选取重过载时长、最大有功负载率、平均有功负载率、重三相不平衡时长、最大三相不平衡度以及平均三相不平衡度作为停电特征向量，利用Embedded特征选择方法进行配变最优停电特征的选择，选用Logistics回归作为基分类器，惩罚项选用L1范数，惩罚项权重取0.45，得到配电变压器最优停电特征子集。

选取某地区供电公司实际1 265条数据作为样本数据，对本文提出的快速Logistic最小误差熵模型进行验证。将数据随机分为训练集和验证集2个部分，其中训练集占80%，验证集占20%。表2中给出特征变量的样例。

表2 训练集中的特征变量数据样例

Tab. 2 Sample of feature variable data in training set

序号	标准化后的重过载时长	最大有功负载率/%	平均有功负载率/%	平均三相不平衡度/%	标准化后的重三相不平衡度	模型输出结果
1	0	74.98	78.06	52.60	0	1
2	0.010 53	87.14	46.89	20.17	17.570 000	1
3	0.125 70	131.58	32.45	38.16	0.012 300	0
4	0.025 96	97.10	29.74	23.15	0.001 366	0
5	0.083 33	123.86	35.80	35.15	0.002 732	0

新窗口打开| 下载CSV

在训练集上运行Logistic快速最小熵算法，得到预测模型的参数 $\hat{w}$ ：

\hat{w} = {[- 0.061 0.007 4 - 0.26 0.61 0.032 0.052]}^{T}

(21)

然后利用测试集对配电变压器的停电概率进行预测，测试集的部分输出结果如表3所示。

表3 测试集中的部分预测结果

Tab. 3 Partial prediction results in test set

序号	标准化后的重过载时长	最大有功负载率/%	平均有功负载率/%	平均三相不平衡度/%	标准化后的重三相不平衡度	实际停电情况	模型预测输出	输出停电概率
1	0.095 62	115.92	31.37	34.44	0	0	0	0.000 0
2	0.019 13	97.14	25.38	26.40	0	0	0	0.000 0
3	0.062 84	125.54	35.19	32.72	0.120 2	0	0	0.000 0
4	0.124 50	136.80	31.84	31.84	0.019 91	1	0	0.000 0
5	0.278 70	95.22	100.90	34.27	0	1	1	1.000 0

新窗口打开| 下载CSV

使用错误率和F测量2种评价标准对模型的预测结果进行评价。Logistic快速最小熵算法的停电预测结果见表4，可以看出，算法预测的准确率在88%左右，表明配电变压器的停电预测模型较为稳定，可以对是否停电进行区分，能够辅助运维人员预测设备的停电情况，并根据设备停电情况对有停电隐患的设备进行有针对性的关注和管理，减少停电的发生。

表4 Logistic 快速最小熵算法预测结果评价

Tab. 4 Evaluation of prediction results of Logistic fast minimum entropy algorithm

算法	错误率	F测量
Logistic快速最小熵算法	0.118 5	0.877 2

新窗口打开| 下载CSV

3.3 配电网停电预测方法的对比分析

本文对Logistic快速最小误差熵算法以及Logistic回归算法的预测效果进行对比分析，并采用与Logistic最小误差熵预测模型相同的数据集。

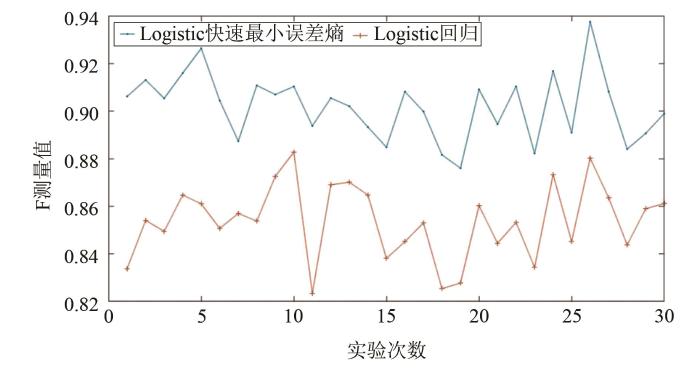
对2种算法分别进行30次预测，图1是2种算法预测结果的F测量评价。从图1中可以看出，2种算法的F测量值都在0.80以上，但Logistic快速最小误差熵的预测效果要明显好于Logistic回归的效果。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 2种算法停电预测结果的F测量

Fig. 1 F-measurement of outage prediction results based on two algorithms

4 结论

在最小熵回归算法的基础上，提出了快速最小误差熵算法，基本保持了最小熵回归的回归效果，并且显著地减少了算法的运行时间；针对配变停电预测适用Logistic回归的情况，提出了基于Logistic的快速最小误差熵回归算法，根据供电公司实际数据进行算法验证，预测效果要明显好于Logistic回归的效果。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

尤田柱，鄢志平．配电网安全防护技术[M]．北京：中国电力出版社，2015：125-128．