随着能源绿色化转型的不断深入，电力系统呈现出高比例可再生能源^[1-4]和电力电子设备的“双高”特性。在此背景下，电-氢混合储能微电网^[5]崭露头角，其融合了多种能源，满足了不同电力需求，提供了备用能源，减轻了电网负担，具备多功能性和高定制性。该系统不仅能促进风光能源的消纳，还有助于实现需求响应，增强电网韧性。

过去的研究中已经将储氢与冷热电联产^[6]系统相结合，形成了一个综合能源系统^[7-9]。该系统通过多目标优化算法等手段来优化容量和运行，以协调各种能源转换设备和储能设备，从而为能源消费者提供优质的能源服务。文献[10]构建了一个以绝热压缩空气储能和电氢等集成能源为载体的区域一体化能源系统和双层混合规划模型，实现了可再生能源消纳。文献[11]构建了储氢一体化系统，并采用多目标粒子群优化方法，实现了运行成本与环境成本的平衡。文献[12]建立了考虑电-热-氢协同的独立微电网，并采用智能水滴算法来寻找微电网各组成部分的最优容量。文献[13]提出了一种计及功率交互约束的混合储能微电网容量优化配置方法，以促进电-氢耦合。文献[14]通过考虑氢储系统的动态效率，优化了产氢和耗氢设备的工作区间，制定了合理的微电网运行控制策略。文献[15]建立了包括光伏、燃料电池和电解池的综合能源系统，并以系统经济成本和弃光率最小化为目标进行多目标规划。综上所述，可知该方向现有研究仅关注电氢耦合能源系统，而忽略了不同商业模式对该系统的影响。

为了实现含电-氢混合储能微电网优化问题的有效求解，本文深入研究了非支配排序遗传算法II(non-dominated sorting genetic algorithm，NSGA-II)^[16-18]。该算法是求解多目标问题的经典算法，但其存在计算复杂、主观性强的弱点，并且传统的非支配排序遗传算法只考虑相邻个体间距，群体遗传概率低，存在解分布不均匀的问题，这也导致了其计算结果不稳定，不易获得全局最优解。因此，亟需对该算法进行增强改进，以提高算法的寻优能力。

为此，本文主要研究了基于2种典型商业模式的电-氢混合储能微电网优化运行调度问题，构建了电-氢混合储能微电网通用数学模型和基本拓扑结构，给出了不同商业模式下的优化调度模型与包含物理意义的约束条件，并改进了增强的非支配遗传排序算法，实现了优化调度模型的高效求解，为后续该领域的研究提供了参考。

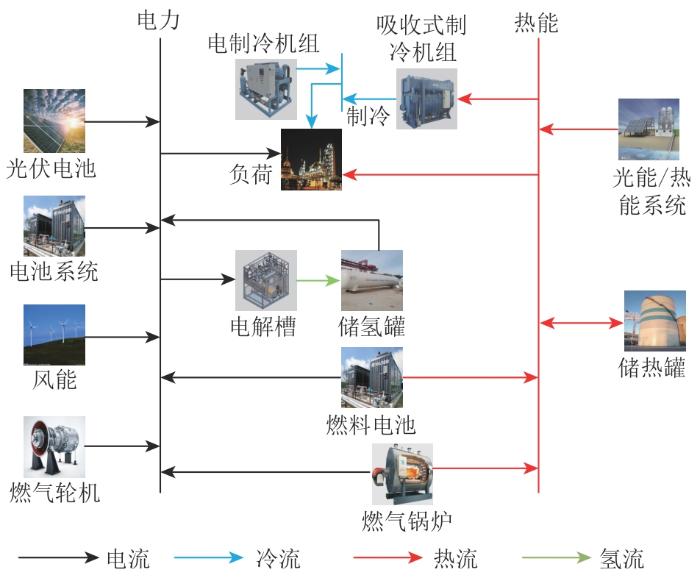
多能源微电网结构如图1所示，本文以该结构为基础对微电网系统进行数学建模。该微电网结构基于实际工程背景设计，旨在解决传统能源供应系统存在的高耗能问题，提高风光出力水平，实现节能减排。由图1可知，系统主要包括风力发电、太阳能发电、储能设备和燃气发电等多种能源设备，以多能协调互济的方式，为用户提供可靠、高效和环保的能源供应服务。

风电机组的功率曲线反映风速与风电输出功率之间的关系。长期风速概率统计特性符合两参数威布尔分布的概率密度函数^[19]及累积分布函数^[20]，其表达式分别如下：

式中：u为在1~15min较大时间粒度下的平均风速；f(u)为概率密度函数；F(u)为累积分布函数；b为威布尔分布的尺度参数；κ为威布尔分布的形状参数，κ>0，一般通过威布尔分布拟合历史风速数据得到。

风力发电的原理是利用风力驱动涡轮机，将机械能转化为电能。风机的输出功率与风速之间的关系式如下：

式中：PWTt为t时刻风电机组的实际输出功率；Pen为风电机组的额定输出功率；urate,b、uin,b分别为当威布尔分布的形状参数为b时的额定风速、切入风速；uin、uout分别为风电机组的投入、退出风速；uen为风电机组的全功率输出风速；Pin为初始输出参考功率。

光伏电池最大输出电流Imax,PV表达式如下：

式中：Ish,PV为光伏电池短路电流；Umax,PV为最大输出电压；Uc,PV为光伏电池开路电压；C1、C2均为光伏电池工程系数^[21]。

光伏发电系统运行时易受到多种环境因素的影响，所以其输出功率并不稳定，其中光照强度和环境温度对光电系统的影响最为显著，所以光伏发电系统在给定环境条件下的数学模型为

式中：PPVt为光伏发电系统的输出功率；TSC、GSC分别为标准测试条件下的环境温度和辐射强度；PPVrate为TSC=25 ℃、GSC=1 000 W/m²时光伏发电系统的额定输出功率；k=-0.0047，为温度系数；GPV为光伏发电系统实际接收的光照强度；TPV为实际环境温度。

燃气锅炉作为系统中的辅助供能设备，在系统出现能量缺额时，通过燃料系统、风烟系统和汽水系统将天然气中的化学能转化为热能，从而为用户提供所需能量，其表达式如下：

式中：QBt为t时刻燃气锅炉的输出热能；GNatt为t时刻燃气锅炉燃气消耗量；ηB为燃气锅炉的效率。

在光-储互补冷热电联供(photo-storage combined cooling heating and power，PS-CCHP)系统中，储热罐根据热能平衡确定运行状态。当系统中热能充足时，储热罐将多余热能吸收作为热负荷备用；当系统中热能缺乏时，储热罐释放热能保证用户热能需求得到可靠供应。因此，储热罐使得系统输出热能与用户热负荷需求在时间上更加匹配。与蓄电池工作原理相似，储热罐也包含3种工作状态，分别为储热、吸热和放热。储热罐的数学模型为

式中：QSTt和QSTt-1分别为储热罐在t和t-1时刻储存的热能，若QSTt≥0，则储热罐放热，若QSTt<0，则储热罐储存热量；ηls、ηch和ηds分别为储热罐的热损失率、吸热效率、放热效率；Qcht、Qdst分别为t时刻储热罐吸收、释放的热能。

为了延长储热罐的使用寿命，需要对其储存的热能和某时刻吸收、释放的热能进行限制，储热罐安全限制的约束条件为

式中：QSTmin、QSTmax分别为储热罐最低、最高热能限制；Qchmax、Qdsmax分别为储热罐单位时间最大吸收、释放热能限制。

为了保证用户制冷需求得到可靠满足，设置了以电能驱动的电制冷机组。电制冷机组根据逆卡诺循环原理，通过压缩机、冷凝器、蒸发器等器件为用户制冷。电制冷机组首先利用压缩机将气态的制冷剂压缩为高温高压状态；然后，将制冷剂送入冷凝器，制冷剂与外界进行热量交换后形成液态冷凝剂；最后，将液态冷凝剂送入蒸发器中，由于蒸发器中压力减小，冷凝剂迅速气化，吸收室内热量，达到为用户制冷的效果。电制冷机组整个制冷过程中消耗的电能由PS-CCHP系统提供。电制冷机组的数学模型为

式中：QACt为t时刻电制冷机组的输出制冷量；EEC为消耗电能；ηAC为电制冷机组的能效系数。

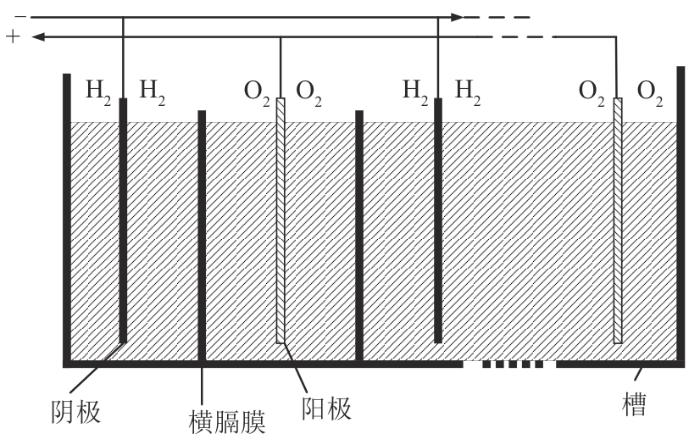
本文采用碱性电解槽作为制氢单元，其主要由直流连接线、箱体、横膈膜、电极、电解液组成，结构如图2所示。

电解槽阴阳两极发生的反应式如下：

电解槽产氢量表达式如下：

式中：Uel为电解槽电压；N0为电池串联个数；E为单个电解槽的开路电压；Rel为等效电阻；I为回路电流；Uc,el为单个电解槽的工作电压；E0为标准电动势；T为电池温度；F为法拉第常数；xH2、xO2、xH2O分别为输入H₂、O₂和H₂O的摩尔分数；nH2为产生氢气的物质的量^[22]；ηF为法拉第效率^[23]；net为电解槽串联数量；Iet为电解槽等效电流。Iet与电解槽两端电压Uce的关系式为

式中：Ure为电解槽可逆电池电压；r1和r2均为电解液欧姆参数；Tel为电解液温度；Iel为电解槽电流；Ael为电极面积；s1、s2、t1、t2、t3均为电极过电压参数。

电解槽制得的氢气通过压缩机加压后存入高压气态储氢罐，储氢罐储氢量表达式为

式中：HINt为t时刻的氢气储存量；Tt为t时刻高压储氢罐温度；pt为t时刻高压储氢罐压力；Rfe为气体常数。

选择氢氧燃料电池组作为系统燃氢发电单元，燃料电池输出特性方程如下：

式中：Ufe为燃料电池电压；N1为燃料电池串联个数；Uc,fe为燃料电池开路电压；rfe为燃料电池内阻；Ife为燃料电池回路电流；Tfe为燃料电池温度，K。

燃气轮机是消耗天然气产生电能和热能的设备，其数学模型如下：

式中：GGT为燃气轮机天然气消耗量；PGTt为燃气轮机输出功率；Δt为时间差；ηGT为燃气轮机效率；L为天然气热值；QGT为输出热功率；η1为热损失系数；η为系统的整体效率。

吸收式冷水机组输入热功率与输出冷却功率的关系式为

式中：Qtar和Ptar分别为t时刻吸收式冷水机组的冷功率输出和热功率消耗；Kar表示吸收式冷水机组的能效系数。

该设备的回收热量QRe计算式为

式中：Tsy为系统产生的热量；ηRe为余热回收系数；ηe为发电机组效率。

电池与锂辉石^[24]正极相结合组成超级电容(super capacitor，SC)，大大提高了混合储能系统的技术经济指标。由于单个SC存储的能量有限，不能承受高电压，一般需要通过串联或并联的方式扩大其使用范围。设SC组串联或并联，则SC组的等效电容C为

式中：n为SC的并联数量；m为SC串联数量；Cf为SC的单体电容。

设Umax和Umin分别为SC组的最大电压和最小电压，则储能功率Qu表达式为

式中Us,max和Us,min分别为单个SC的最大和最小电压。

目前，在电力体制改革的背景下，电-氢混合储能微电网的商业模式可分为2种：多方合作供能和多方独立供能商业模式^[25]。

在多方合作供能的商业模式下，微电网中各出力源合作协同，组成一个整体。该模式强调集体思维，以整个微电网的最优运行为目标，不考虑单个出力源的效益得失。

本文多方合作供能模式以经济成本和环保成本最小为目标函数，其优化调度模型可表示如下：

式中：Fed1为多方合作供能模式下的总目标函数；fi为第i个目标函数。

第1个目标函数f1是最小化系统的经济成本，包括t时刻购买天然气的成本CNatt、从电网购电的成本CGt、设备的运维成本COt、污水费用CWt、CO2排放成本CCO2t及出售氢能的成本CH2t。其表达式如下：

式中：cNat为天然气的市场价格；cBt、cSt分别为t时刻电网的实时购电价格、售电价格；CO,GT、CO,WT、CO,PV、CO,AC、CO,B、CO,EH、CO,A、CO,FU、CO,ST和CO,AB分别为t时刻燃气轮机、风力发电机、光伏、吸收式制冷机、燃气锅炉、电解槽、蓄电池、燃料电池、储热罐和二氧化碳吸收装置对应的运维费用；PEHt、PFUt分别为电解槽、燃料电池的功率；MCO2为电解槽吸收的CO2质量；QAt为蓄电池的热负荷；σ为燃气轮机单位污水处理成本；τ为单位CO2排放成本；XCO2t为t时刻碳排放总量；ϑ为氢气的退出价格；HSAt为售出氢气的量。

第2个目标函数f2是最小化系统的环保成本，包括电网的碳排放和天然气的碳排放。其表达式如下：

式中：TCO2t为t时刻的总排碳量；CV,Nat为天然气的最高热值；μNat和μG分别为天然气和电网的排放因子；ρ为每产生1 m³氢气吸收的CO2量；HEHt为t时刻电解槽的产氢能力；GBt和GMTt分别为t时刻燃气锅炉和燃气轮机所消耗的天然气量。

多方独立供能的商业模式多存在于美、欧等国家和地区，在该模式下，微电网各组成部分独立运营，分属于不同的权利主体。多方独立供能模式强调经济收益，各个出力源均以经济最大化为目标，而不再考虑环保性等其他因素。本文所建立的微电网模型中涉及独立盈利供能主体的共有3个部分，分别为风力发电商、光伏发电商和电氢可逆储能商；其他部分为安全保供设备，不涉及独立运营。经济调度模型如下：

式中：Fed2为多方独立供能商业模式下的总目标函数；Swind为风力发电商售电净收益；Ssolar为光伏发电商售电净收益；SH2为电氢储能商售氢净收益。特别需要强调的是，在该模式下，因可再生能源独立运营、自负盈亏，因此不涉及弃风弃光成本。

本文的电-氢混合储能微电网系统通过热、电、氢供给的能量平衡，确保各个环节之间的协调与稳定。系统中各设备的输出功率，包括燃气轮机、燃气锅炉、电解槽、蓄电池等，均受到严格的上、下限约束，以实现高效的能量转换和负荷调节。

1）热平衡约束

在t时刻，用户和制冷所需的热电主要由燃气轮机发电产生的余热、燃气锅炉输出的热电，以及电解水和燃料电池产生的余热提供。本文考虑的电-氢混合储能微电网系统热平衡约束为

式中：ηh为热交换器的效率；QREt、QEHt、QFUt和QLDt分别为t时刻燃气轮机余热、电解槽产生的余热、燃料电池产生的余热和用户所需热功率。

为了进一步分析电制冷系统的效率和负荷需求，提出了以下电制冷负荷平衡方程：

式中：QCOt为t时刻用户需要电制冷机提供的负荷；Θ为冷却系数。从式(39)可知，吸收式制冷机在t时刻提供给用户的冷负荷QACt。

2）电平衡约束

本文考虑的电-氢混合储能微电网系统电平衡约束为

式中：PGt为微电网与电网的交互电量，如果PGt<0，表示在t时刻向电网售出电量，否则表示t时刻从电网购买电量；PAt为蓄电池在t时刻的功率，如果PAt>0，表示放出电能，否则为补充电能。

3）氢平衡约束

在满足氢气需求的前提下，将电解槽产生的氢气出售或储存在储氢罐中，其平衡式如下：

式中：HLDt为t时刻用户需要的氢气量；HSAt为t时刻氢气销售量。

4）燃气轮机出力约束

为了确保燃气轮机运行在设计范围内，其输出功率需要满足以下条件约束：

式中PGT,MAX和PGT,MIN分别为燃气轮机输出功率的上、下限。

5）燃气锅炉出力约束

为了保证燃气锅炉在安全高效的条件下运行，其输出热功率须满足以下限制条件：

式中QB,MAX为燃气锅炉的最大热功率。

6）光伏出力约束

光伏系统的功率输出受环境条件影响，因此其输出功率必须遵循以下约束：

式中PPV,MAX和PPV,MIN分别为光伏功率的上、下限。

7）风力发电机出力约束

风力发电机的输出功率受到风速等因素的影响，因此须满足以下约束条件：

式中PWT,MAX为最大的风机输出功率。

8）产氢耗电功率约束

电解槽的产氢过程需要消耗电能，其功率需求必须满足以下约束条件：

式中PEH,MAX和PEH,MIN分别为电解槽产氢所需功率的上、下限。

9）燃料电池出力约束

在实际运行中，燃料电池的输出功率必须在以下范围内：

式中PFU,MAX和PFU,MIN分别为燃料电池输出功率的上、下限。

为了确保蓄电池的安全和高效运行，其输出功率需要符合以下约束条件：

式中PA,MAX和PA,MIN分别为蓄电池输出功率的上、下限。

11）吸收式制冷机耗能约束

吸收式制冷机的热功率输出必须在设计容量内，具体约束条件为

式中QAC,MAX为吸收式制冷机的最大热功率。

NSGA-II算法^[26]由Deb等学者于2002年首次提出。该算法在原始的NSGA算法基础上引入了快速非支配排序、精英策略和拥挤度排序等创新策略，降低了NSGA算法计算的复杂度，提高了算法的运算效率和鲁棒性，保证了非劣最优解的均匀分布。NSGA-II算法的原理与进化算法相似，通过一代代的迭代更新，保留适应当前环境的个体，从而实现寻优。NSGA-II算法的核心计算步骤如下：

1）初始化。在多目标优化问题的决策变量空间内，使用拉丁超立方体采样(Latin hypercube sampling，LHS)随机生成一组个体，形成初始种群。

2）适应度计算。为种群中的每个个体计算其在多目标空间中的适应度值。

3）非支配排序和拥挤度排序。对种群进行非支配排序和拥挤度排序。

4）生成新种群。通过二元锦标赛选择、变异及正态分布交叉(normal distribution crossove，NDX)操作，从父代种群中生成子代种群。

5）种群合并和排序。将父代种群和子代种群合并，然后对合并后的种群进行快速非支配排序和马氏拥挤密度估计。

6）精英策略。采用精英选择策略对种群进行修剪，生成新的父代种群。

7）迭代终止条件。如果算法的迭代次数达到预定的最大迭代次数，算法终止并输出非支配解；否则，回到步骤2，继续迭代。

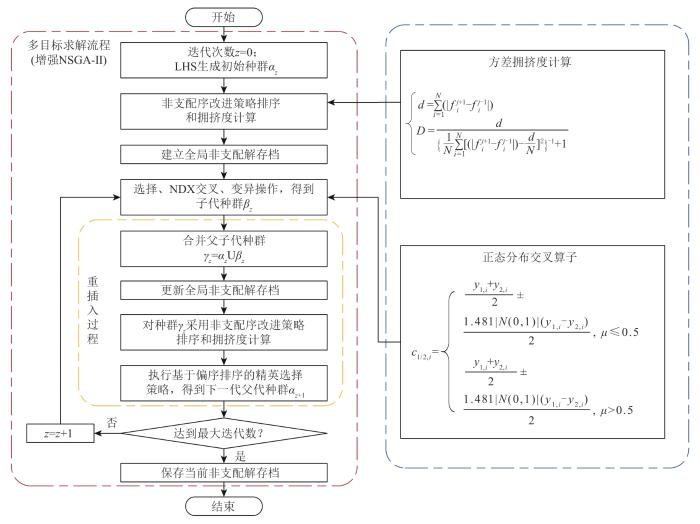
增强后的NSGA-II算法的主要增强点包括新的方差拥挤度计算方法和正态分布交叉算子2个方面，流程如图3所示。

1）方差拥挤度计算

在NSGA-II算法核心步骤3）中，传统的拥挤度计算方法仅考虑相邻个体之间的距离，导致群体的遗传概率较低且解的分布不均匀。为了解决这一问题，引入方差因子来优化解的分布，从而提升群体的遗传概率。这样做不仅有助于提高解的多样性，还能促进种群更均匀地覆盖解空间。方差拥挤度计算式如下：

式中：d为方差因子；D为拥挤度；fij-1、fij+1分别为排序后第j-1、j+1个个体第i个子目标的函数值；N为种群总数。

2）正态分布交叉算子

在NSGA-II算法核心步骤4）中，标准交叉操作常导致计算结果不稳定，难以获得全局最优解。为了解决这一问题，引入正态分布交叉算子。与原标准交叉方式相比，正态分布交叉算子进一步扩大了算子的搜索空间，提高了算法全局搜索能力，保障了帕累托(Pareto)前沿^[27]的均匀性和完整性。正态分布交叉算子表达式如下：

式中：c1/2,i为经过交叉算子生成的2个子代个体中对应的第i个决策变量；y1,i、y2,i分别为2个父代个体中对应的第i个决策变量；1.481N(0,1)为正态分布参数；μ为一随机数，μ∈[0,1]。

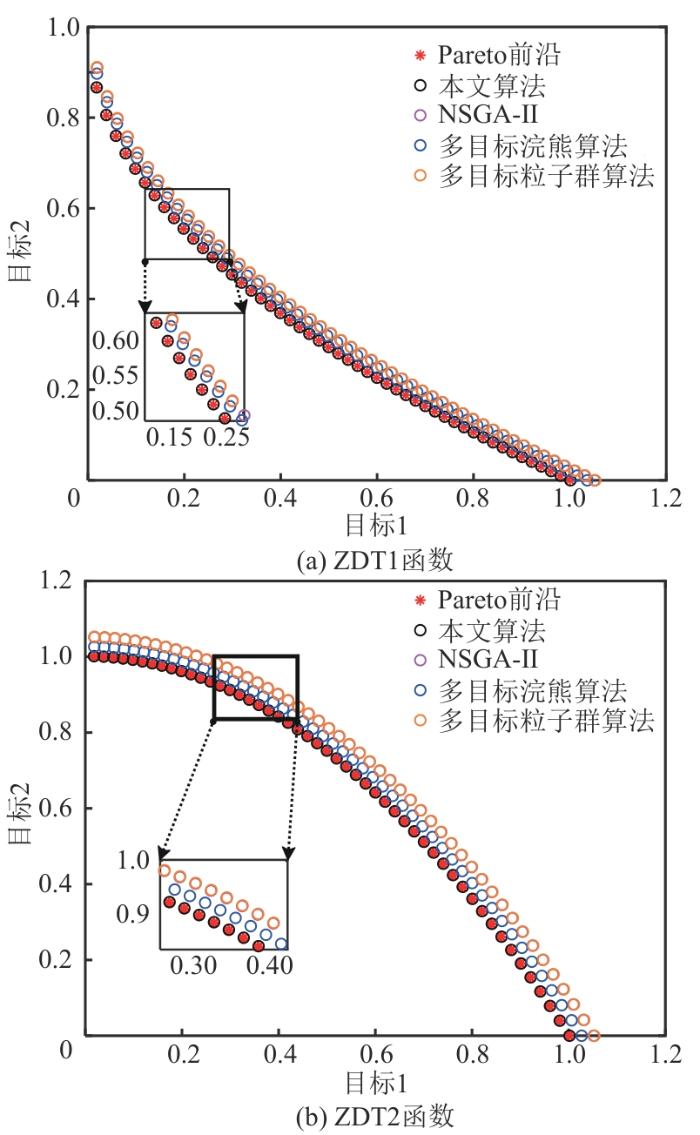
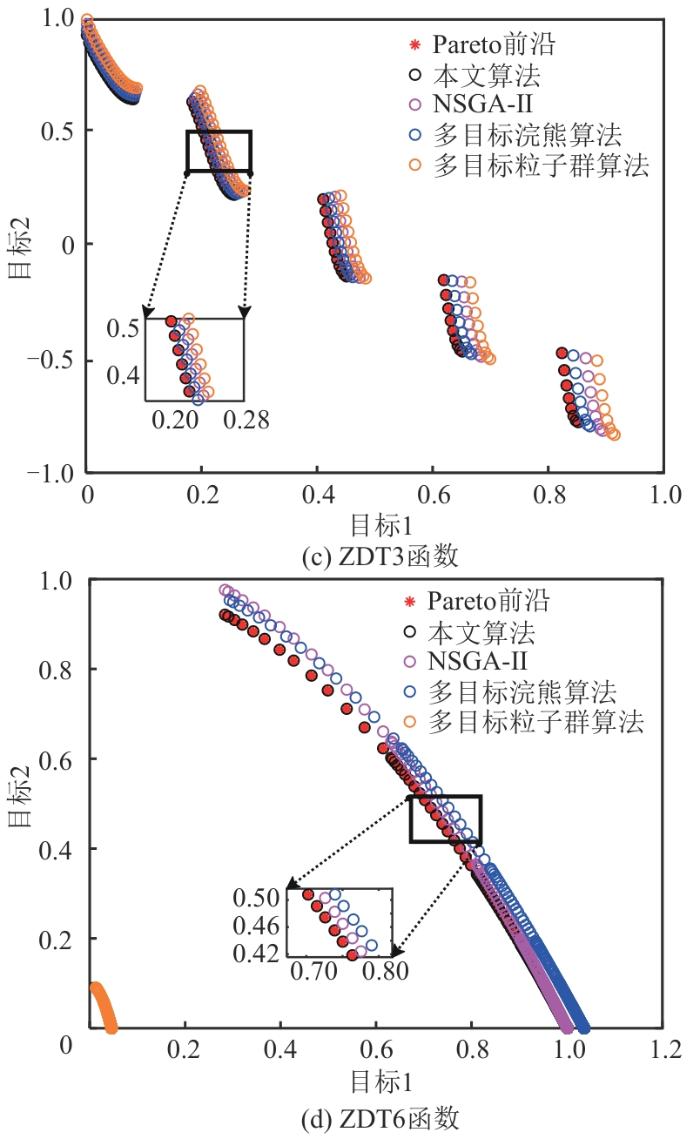
为验证所提出的改进算法的性能，将本文算法与传统NSGA-II算法、多目标浣熊算法、多目标粒子群算法进行比较，并利用上述算法分别求解多目标优化问题标准测试函数集^[28]中的ZDT1^[29]、ZDT2^[30]、ZDT3^[31]和ZDT6^[32]函数，最终得到了如图4所示的测试函数仿真计算结果。为了更好地比较各算法的性能，图4中还绘制了上述4个函数的理想Pareto前沿。本文计算过程均在搭载了i5-137000F处理器、8 GB 2 600 MHz单通道内存和蓝宝石RX580-super显卡的电脑上进行。此外，4种算法参数均相同，设置的初始种群为500，迭代次数为1 000，交叉率为85%，变异率为5%，聚类数为20。

由图4可以看出，本文所提算法搜索出的Pareto前沿最接近各个测试函数的最优解，表明其准确性高于其他3种算法。为进一步验证本文算法的性能，以平均值、标准差、反世代距离评价(inverted generational distance，IGD)指标和Spacing指标4个定量评价指标对上述4种算法进行比较分析。计算结果如表1所示。

对表1数据进行分析可知：在上述4种测试函数所代表的多目标优化问题中，本文所提算法在各项评价指标方面均显著优于其他3种算法。具体而言，与传统NSGA-II算法、多目标浣熊算法、多目标粒子群算法相比，本文算法的平均值指标分别提高了45%、32%和51%，验证了算法的高准确性；标准差指标分别减小了0.014、0.010和0.021，表明了本文方法的性能更为稳定；IGD指标和Spacing指标均提高了约45%，表明了本文所提算法的解集更富有多样性和均匀性。综上所述，本文提出的增强NSGA-II算法能够高效地应对多目标优化问题。

为了验证本文所提算法在求解含电-氢混合储能微电网优化调度问题中的有效性，并探索各商业运营模式的优劣，以东南沿海某地电-氢混合储能系统为例，进行仿真分析。本文每天对系统优化24次，单次优化时间间隔为1 h，系统具体参数见文献[23,33]。

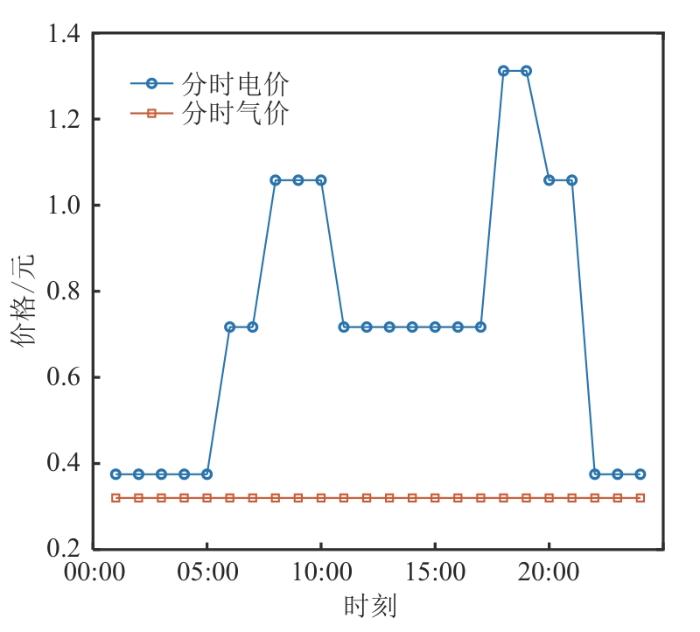
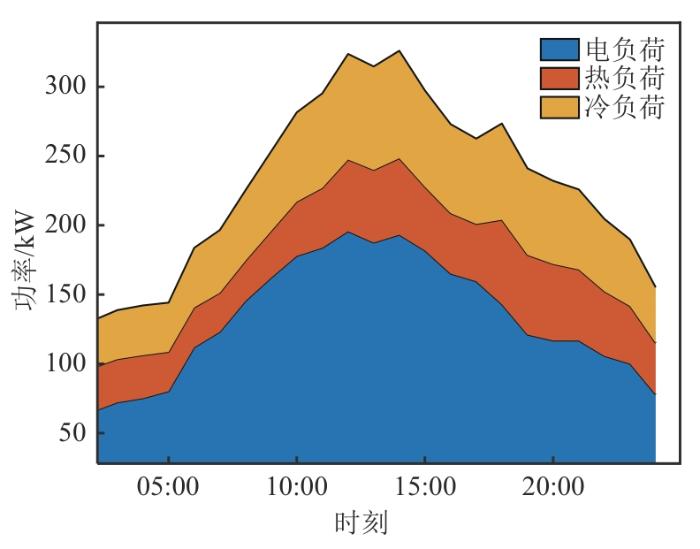
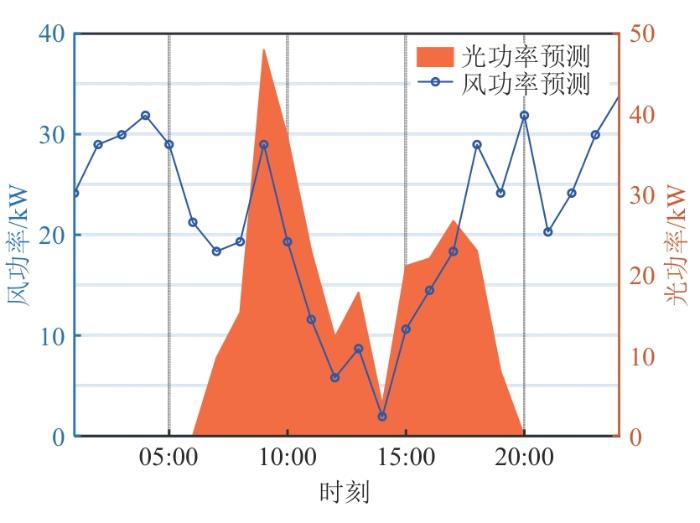
该系统对应的电价和气价、冷热电负荷以及风光功率等基础数据分别如图5—7所示。

由图5可知，该系统所在区域前日22:00—05:00是电价低谷时段，08:00—10:00是电价高峰时段，18:00—20:00是电价尖峰时段，其余时间为电价平期。与其他国家不同，我国天然气价格未实行波动气价，全天价格均为3.2元/m³。由图6可知，该地的冷热电负荷呈现白天高、夜间低的趋势。对该系统进行优化调度的目的是提高新能源消纳比例，提高系统经济效益。由图7可知，该系统风光出力呈现互补态势：风电出力夜间多、白天少，极大、极小值分别出现在24:00和14:00；光伏出力呈现出驼峰状态，2个峰值分别出现在10:00和17:00，而在14:00时出现最小值。图7的光伏出力曲线趋势与理论出力曲线不符，后经查阅该电站日志，发现当日14:00光伏电站所在地正在下雨，影响了光伏出力。

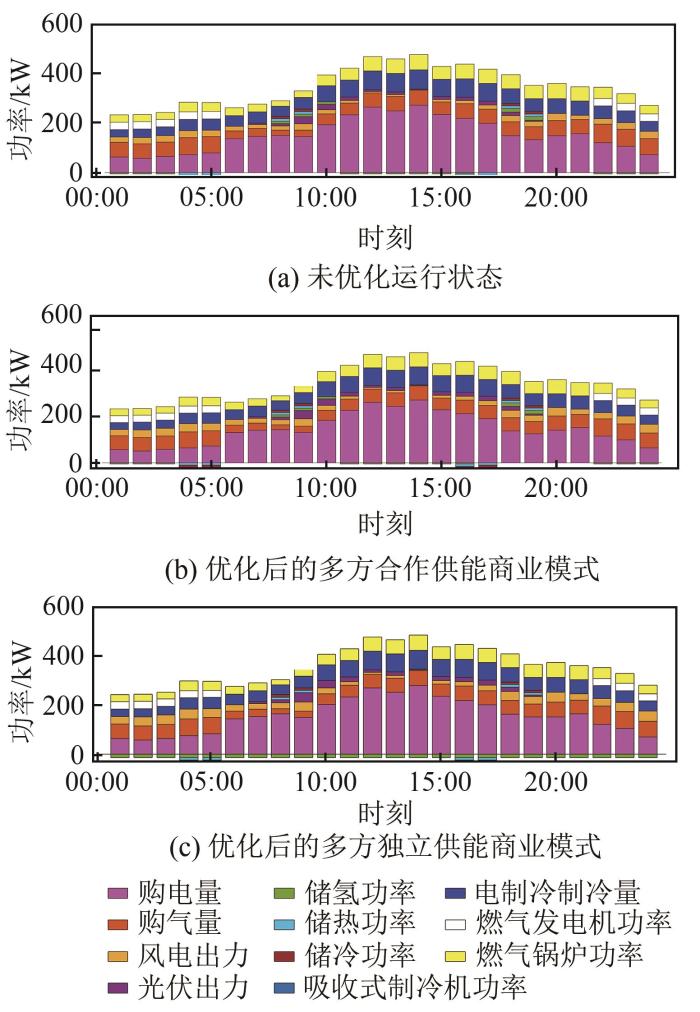
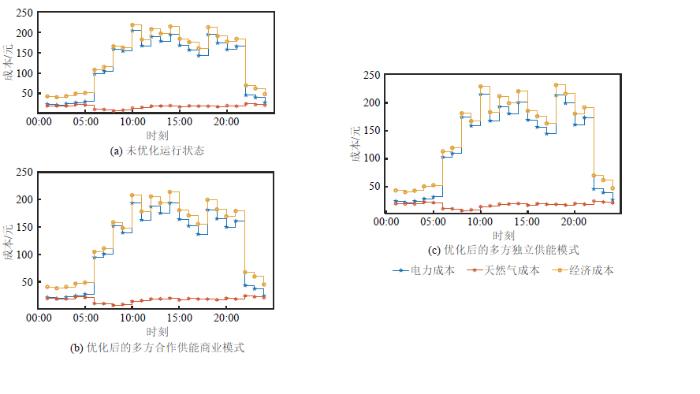
使用本文所提方法分别对2种不同商业运行模式下的系统进行优化调度，其结果如图8所示，各调度结果分时运行成本如图9所示，其中经济成本为电力成本与天然气成本的和。

由图8可知，经优化后的2种商业运行模式与未优化时相比，新能源出力明显增加，弃风弃光情况减少，验证了本文所提优化算法的有效性。综合图8和图9可知，与多方独立运营模式相比，多方合作运营模式经济性表现更好，但多方独立运营模式的弃风弃光率表现更好，具体指标如表2所示。

由表2可以看出：与优化前相比，优化后的多方合作供能商业模式的系统经济性提高了近4.1%，弃风、弃光率降低了约19%，全天减少碳排放量129.91 kg；而多方独立供能商业模式虽然实现了风电光伏的全部消纳，全天碳减排量提升了40%，但其经济性较多方合作供能模式降低了8%。这是因为在多方独立供能模式下，各出力电源只注重自身经济效益，而忽视了系统的整体经济性和安全性。电氢转化储能装置仅负责制氢贩卖，而不再承担保供职责，导致系统整体最优被舍弃。因此，从系统整体角度出发，多方合作供能商业模式显然优于多方独立供能商业模式。

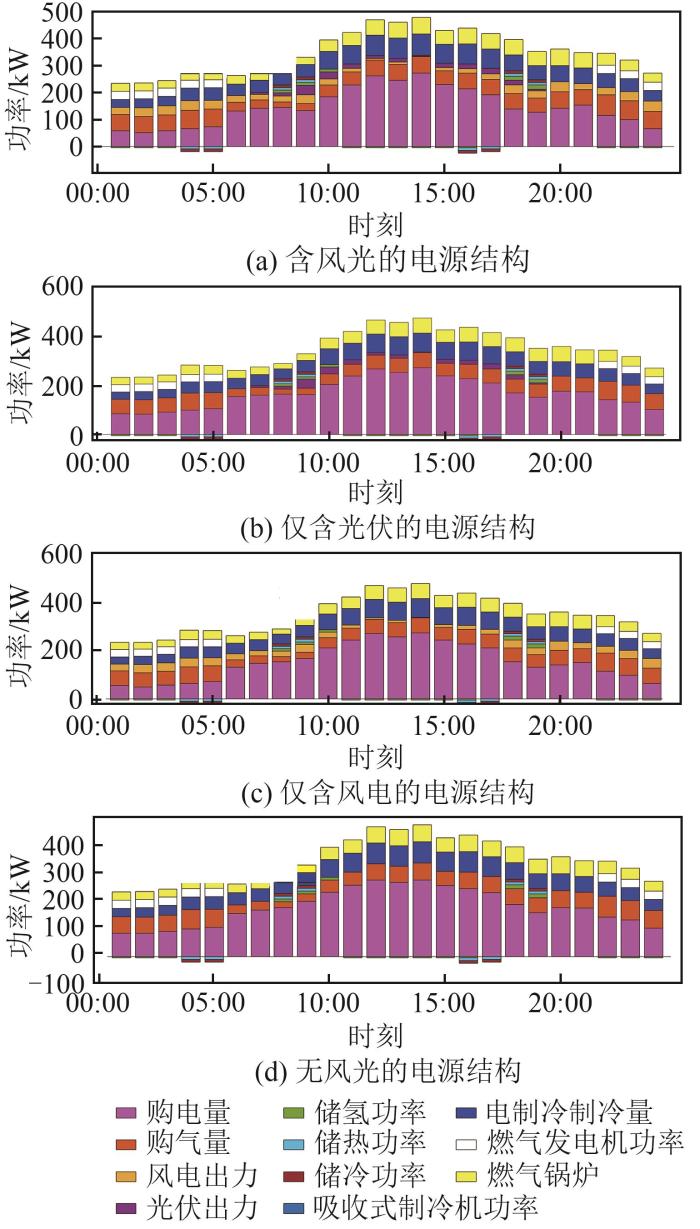
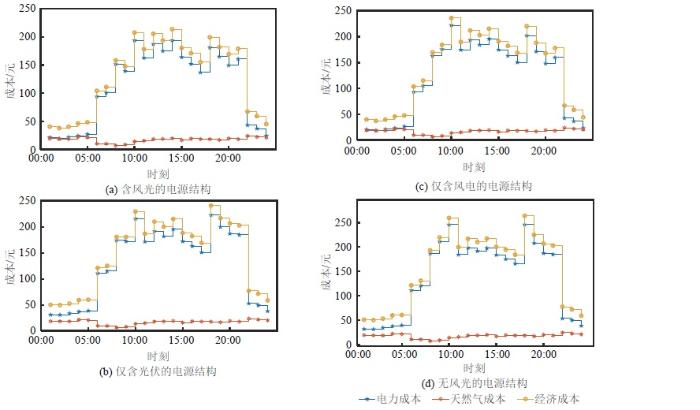
由4.1节可知，多方合作供能的商业模式更适合我国电力市场，因此，在多方合作供能商业模式的基础上继续分析不同电源结构对优化结果的影响，最终的优化调度结果如图10所示，各结果分时运行成本如图11所示。

结合图10和图11可以看出，不同电源结构对最终优化结果产生了不同的影响：当电源结构含有风电和光伏时，优化效果最好；其次是仅含风电的情况；在无风光的电源结构中优化效果最差。为了更好地定量比较，给出了各个不同电源结构优化结果的重要参数，如表3所示。

由表3可以看出，仅含风电或光伏的电源结构弃风、弃光率均优于同时含风光的情况。与同时含风光的弃风、弃光率相比，仅含风电的电源结构弃风率和仅含光伏的电源结构弃光率均降低了约3%，但两者的碳减排量却分别减少了144.18 kg和453.96 kg。这是因为仅含风电和仅含光伏的新能源装机量少于同时含风光的情况，从侧面说明了新能源消纳的难易程度与其装机占比成正比。此外，本文算法在无新能源装机(即传统电源结构)下的优化效果不好，说明整个微电网系统的不确定性主要来源于风电和光伏等可再生能源，而传统电源结构可控可调，稳定性较好。

结合实验与仿真，总结了2种商业模式，提出了一种基于增强的NSGA-II算法的优化方法，使用该方法可以有效提高系统运营的经济性，实现提质增效。具体结论如下：

1）经过算例分析发现，关注系统总体收益的多方合作供能的商业模式更符合我国电力市场的基本情况；而多方独立供能的商业模式不仅忽略了系统的安全性，而且其总收益相较前者降低了8%。

2）使用所提优化方法对多方合作供能的商业模式进行优化后，系统经济性提高了4.1%，系统弃风、弃光率降低了约19%。

3）不同的电源结构对系统运行优化结果具有不同的影响，含风光2种可再生能源的系统优化潜力最大，这说明系统的不稳定性主要来源于风光等可再生能源。

4）所建立的模型还存在一定的局限性，例如未对商业模式进行更加细化的总结，未考虑系统模型的启停成本、设备折旧，以及将天然气价格设为固定单价等。对于上述局限和不足，在后续工作中将进一步展开研究。