稀土钡铜氧化物闭环超导葫芦形环片堆叠磁体的机械特性分析

doi:10.12096/j.2096-4528.pgt.24126

稀土钡铜氧化物闭环超导葫芦形环片堆叠磁体的机械特性分析

王婷, 王银顺, 郭丽宁, 卞雨妍, 连占英, 李乐依, 毛承鹏

华北电力大学电气与电子工程学院，北京市昌平区 102206

Mechanical Characteristics Analysis of Stacked Magnet of Rare Earth Barium Copper Oxide Closed-Loop Superconducting Gourd-Shaped Loop

WANG Ting, WANG Yinshun, GUO Lining, BIAN Yuyan, LIAN Zhanying, LI Leyi, MAO Chengpeng

School of Electrical and Electronic Engineering, North China Electric Power University, Changping District, Beijing 102206, China

收稿日期: 2024-07-01 修回日期: 2024-07-31

基金资助:

国家自然科学基金项目. 52377024

Received: 2024-07-01 Revised: 2024-07-31

作者简介 About authors

王婷(2000)，女，硕士研究生，研究方向为超导电力技术，tingw0401@163.com；

王银顺(1965)，男，博士，教授，研究方向为超导电力技术，本文通信作者，yswang@ncepu.edu.cn；

郭丽宁(2000)，女，硕士研究生，研究方向为超导电力技术，gln0831@163.com；

卞雨妍(1999)，女，硕士研究生，研究方向为超导电力技术，964989707@qq.com；

连占英(1997)，男，硕士研究生，研究方向为超导电力技术，1923782974@qq.com；

李乐依(2000)，女，硕士研究生，研究方向为超导电力技术，hhh0217@163.com；

毛承鹏(2001)，男，硕士研究生，研究方向为超导电力技术，1091488870@qq.com。

摘要

目的高场超导磁体在诸多领域都有着很大的应用价值，但第二代高温超导磁体由于焊接技术尚不成熟，无法实现持续电流模式运行。稀土钡铜氧化物(rare earth barium copper oxide，REBCO)闭环超导葫芦形环片堆叠磁体可实现无阻闭环运行，经验证有磁通密度放大和磁通累加的功能，具有高磁场输出的潜质。因此，研究该磁体在大电流、高磁场运行环境下能否维持稳定很有必要。方法通过建立REBCO闭环超导葫芦形环片堆叠磁体的三维有限元模型，分析其在场冷励磁方法下的电磁响应和应力应变分布情况。结果堆叠磁体的单位体积电磁力由圆环的内径向外径逐渐减小，两端层数最大单位体积电磁力较高，而中间层数较低，呈现出“U”型分布特征。此外，应力较大的区域出现在磁体的连接桥部位及圆环与桥的连接部分，此区域易发生形变，是潜在的失超风险区域。结论磁体的应力应变分布特征分析，对改进葫芦形双孔闭环超导片的几何形状和堆叠磁体的结构具有参考价值，对磁体的安全运行具有重要意义。

关键词： 核聚变 ; 高温超导磁体 ; 超导储能 ; 稀土钡铜氧化物(REBCO) ; 堆叠磁体

Abstract

Objectives High-field superconducting magnets have great application value in many fields. Due to the immature welding technology, the second-generation high-temperature superconducting magnets cannot achieve persistent current mode operation. A rare earth barium copper oxide (REBCO) closed-loop superconducting gourd-shaped loop stacked magnet can achieve unimpeded closed-loop operation. It has been verified that it has the functions of flux density amplification and flux accumulation, and has the potential to achieve high magnetic field output. Therefore, it is crucial to study whether this magnet can maintain stability under high current and high magnetic field conditions. Methods A three-dimensional finite element model of this REBCO closed-loop superconducting gourd-shaped loop stacked magnet was established to analyze its electromagnetic response and stress-strain distribution under the field cold excitation method. Results The electromagnetic force per unit volume of the stacked magnet decreases gradually from the inner diameter to the outer diameter of the circular loop, with higher values at both ends and lower values in the middle, it presented a “U” shaped distribution. Additionally, the areas with significant stress are located at the connecting bridge and the junction between the loop and the bridge, making these regions prone to deformation and potential quench risks. Conclusions The analysis of the distribution characteristics of stress and strain of the magnet has a reference significance for improving the geometric shape of the gourd-shaped double-hole closed-loop superconducting sheet and the structure of the stacked magnet, and is of great significance to the safe operation of the magnet.

Keywords： nuclear fusion ; high temperature superconducting magnet ; superconducting energy storage ; rare earth barium copper oxide (REBCO) ; stacked magnets

PDF (4320KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

王婷, 王银顺, 郭丽宁, 卞雨妍, 连占英, 李乐依, 毛承鹏. 稀土钡铜氧化物闭环超导葫芦形环片堆叠磁体的机械特性分析. 发电技术[J], 2024, 45(6): 1039-1047 DOI:10.12096/j.2096-4528.pgt.24126

WANG Ting, WANG Yinshun, GUO Lining, BIAN Yuyan, LIAN Zhanying, LI Leyi, MAO Chengpeng. Mechanical Characteristics Analysis of Stacked Magnet of Rare Earth Barium Copper Oxide Closed-Loop Superconducting Gourd-Shaped Loop. Power Generation Technology[J], 2024, 45(6): 1039-1047 DOI:10.12096/j.2096-4528.pgt.24126

0 引言

第二代高温超导带材稀土钡铜氧化物(rare earth barium copper oxide，REBCO)，具有高临界电流密度和高临界磁场等优越的性能，使得由其制成的高温超导磁体在核磁共振、超导储能以及核聚变等领域有着非常重要的应用前景^[1-3]。

无阻连接在实现持续电流模式(persistent current mode，PCM)磁体的制造中起着至关重要的作用。对于低温超导材料，焊接工艺已经较为成熟，几乎可以实现持续电流模式运行。然而，对于第二代高温超导带材REBCO而言，由于其特殊的多层结构和复杂的化学成分，很难像低温超导材料一样实现传统意义上的无阻焊接，焊接电阻的存在使得由REBCO带材制备的高温超导磁体无法像低温超导磁体一样利用续流开关实现持续电流模式运行，限制了其在PCM及磁共振成像(magnetic resonance imaging，MRI)等领域的应用^[4-6]。

2006年，Lee等^[7]提出了一种利用切缝的高温超导带材形成超导闭环的方案。但是，这些由闭环制成的线圈不紧凑，机械性能弱，应用困难。还有一种方法是利用激光切割技术在加工后的REBCO带上形成圆孔，然后通过场冷励磁方法实现PCM，这种励磁方式对所能提供的背景磁场要求很高，而且最终磁体所能俘获的磁场尚不能追平或者超过背景场^[8]。此外，目前在制备大尺寸的超导带材方面还存在一定的限制。所以上述提出的2种形式的闭环超导磁体都很难实现高磁场输出。

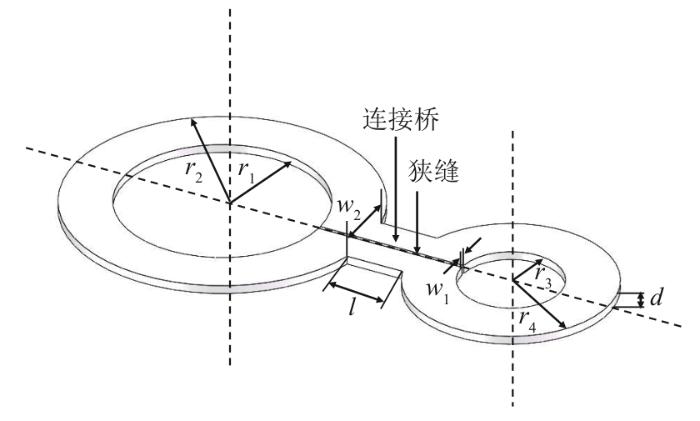
有一种基于REBCO超导片切割形成的葫芦形双孔闭环超导片堆叠组装形成的闭环高温超导磁体可以实现磁通密度放大与累加效果。这种葫芦形双孔闭环超导片是按照哈氏合金、缓冲层、REBCO薄膜、银保护层、铜保护层的顺序加工而成，然后按照需要对外形进行切割。根据闭环超导磁通守恒的原理，这种新型结构的超导片可以实现在小圆孔中磁通密度放大的效果，因此不受超导带材生产技术的限制，将其堆叠成磁体单元后，多个单元组装形成的高温超导磁体最终可以实现磁通密度放大与累加的双重效果，从而实现高场输出^[9]。

然而，REBCO带材由于其多层结构，在法向和切向上的承载能力较弱，因此更容易受到损伤。研究表明，REBCO带材在轴向具有较强的力学性能，能够承受最高达700 MPa的轴向应力。然而，其在横向的承载能力相对较低，能承受超过100 MPa的横向压缩应力和10~100 MPa的横向拉伸应力；在剪切方向上的承载能力则更为有限，通常在30~60 MPa。此外，REBCO带材层间剥离和分离的临界应力非常低，不到1 MPa^[10-11]。

超导带材在制造和使用过程中面临多种应力来源，包括冷却过程中的热失配应力、高磁场中的电磁应力，以及生产过程中产生的机械应力。这些应力可能导致超导带材的分层、剥离和其他形式的损伤^[12-14]。这些损伤会显著降低带材的载流能力，导致电流流向金属层。由于金属层不具备零电阻特性，因此会产生热量，可能触发失超现象，严重影响超导带材的电气和机械性能。

Kolb-Bond等^[15]将带材受单位体积电磁力后产生的偏转角引入了线圈的电磁场分析；Yan等^[16-17]基于文献[15]并考虑了应变对临界电流密度的影响，通过有限元T-A方法分析了超导线圈的磁化过程，数值模拟结果与实验结果符合较好。Mataira等^[18]提出一种径向施加电流的方式，可直接通过有限元方法模拟无绝缘线圈的充电过程。

综上所述，需要考虑这种堆叠磁体在大电流、高磁场环境下运行的机械稳定性问题。当超导体处于磁场下时，电磁应力将作用在导体上，这时高电磁应力会影响超导体的性能。实际工作环境中，超导磁体通常处于电场和磁场中，因此分析这种条件下超导磁体的电磁性能和力学特性是十分必要的。高温超导磁体的实用化取决于其磁稳定性和机械性能。本文通过构建REBCO闭环超导葫芦形环片堆叠磁体的三维电磁力模型，分析其在场冷励磁方法下的电磁响应和应力应变分布情况，为高场磁体的实际应用提供参考。

1 模型建立

1.1 REBCO超导葫芦形环片结构

构成REBCO闭环超导葫芦形环片堆叠磁体的葫芦形环片的结构尺寸见图1，主要参数见表1。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 REBCO超导葫芦形环片结构

Fig.1 Schematic view of REBCO superconducting gourd-shaped loop

表1 REBCO闭环超导葫芦形环片堆叠磁体参数

Tab. 1 Main parameters of REBCO closed-loop superconducting gourd-shaped loop stack magnet

参数	数值
大圆内半径r₁/mm	6
大圆外半径r₂/mm	9
小圆内半径r₃/mm	3
小圆外半径r₄/mm	6
狭缝宽w₁/mm	0.1
连接桥宽w₂/mm	4
连接桥长l/mm	3
环片厚度d/mm	0.1
磁体层数	10

新窗口打开| 下载CSV

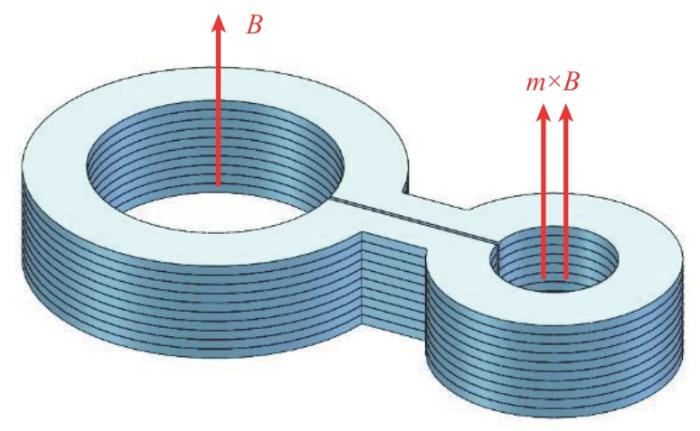
这种葫芦形环片通过不同的堆叠组装成不同的磁通密度放大和磁通累加的磁体，根据适用场合灵活放置使用。图2给出了REBCO闭环超导葫芦形环片堆叠磁体示意图。基于闭环超导磁通守恒的原理，大圆环、小圆环流过相同的电流时，大圆环中产生磁通密度B，小圆环中会产生更大的磁通密度m×B(m>1)。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 REBCO闭环超导葫芦形环片堆叠磁体示意图

Fig. 2 Schematic diagram of REBCO closed-loop superconducting gourd-shaped loop stack magnets

1.2 应力应变计算有限元模型

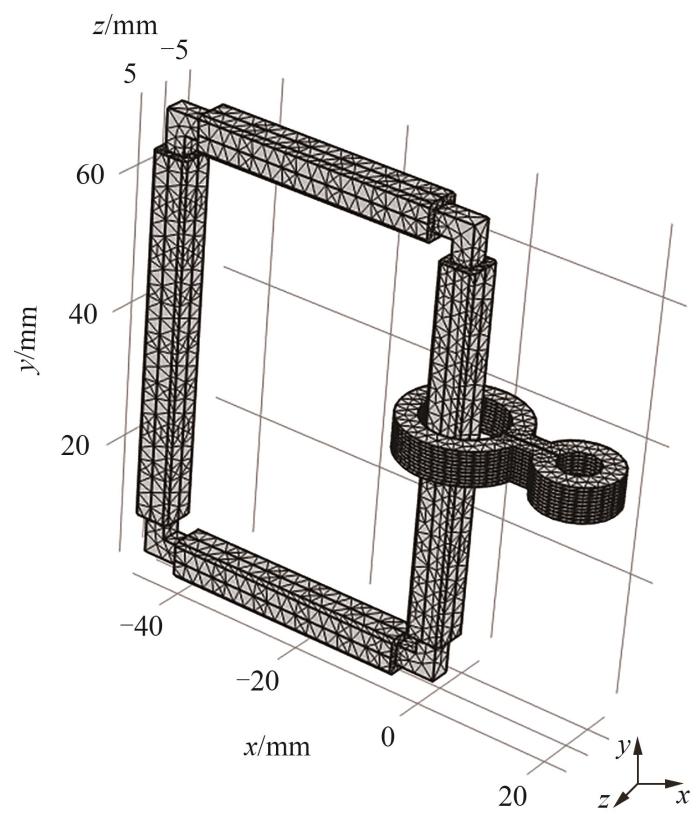
搭建有限元模型的网格划分如图3所示，空气域将磁体、励磁线圈和铁芯包裹，磁体处在空气域中心的位置。为了能详细观察磁体的应力应变分布，在仿真中将REBCO涂层导体的超导层厚度扩大了100倍。为简化模型，只建模了REBCO的超导层来模拟磁体的受力情况，条件是保证超导材料不会失超。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 REBCO闭环超导葫芦形环片堆叠磁体的网格划分

Fig. 3 Schematic diagram of mesh division of REBCO closed-loop superconducting gourd-shaped loop stack magnet

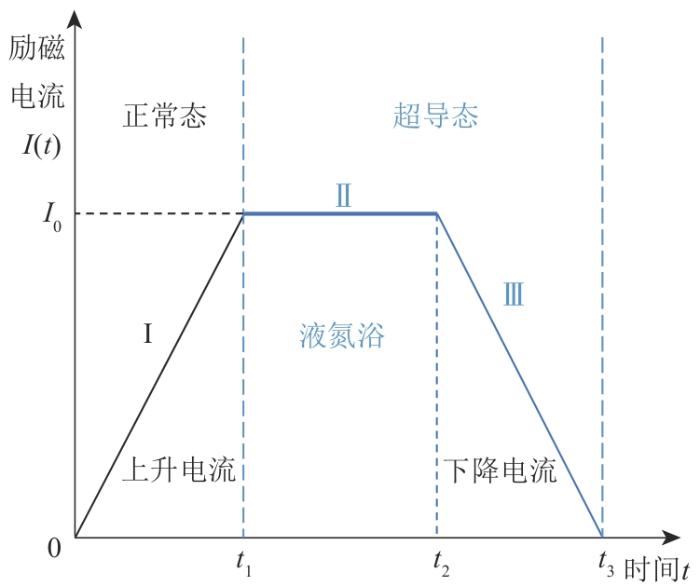
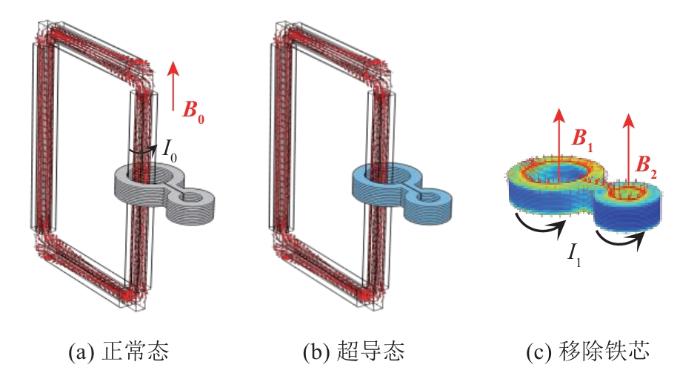
采用场冷励磁方法进行励磁，得到励磁电流时序图如图4所示。给励磁线圈通入电流以提供背景磁场，然后将整个磁体浸入液氮中，磁体进入超导态后，励磁线圈的电流缓慢降至0。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 场冷励磁方法下的励磁电流时序图

Fig. 4 Excitation current timing diagram under field cooling method

根据闭环超导体的磁通守恒，感应电流在大回路和小回路中产生并流动。独特的葫芦形结构使得小回路中心的磁通密度比大回路大^[9]。

场冷励磁方法下REBCO闭环超导葫芦形环片堆叠磁体磁通密度放大原理示意图如图5所示。在初始正常态下，励磁线圈穿过葫芦形回路的大孔。在0—t₁期间，电流I₀通入励磁线圈，在铁芯内产生磁通密度B₀。然后逐渐降低温度至77 K，葫芦形环路进入超导态。在t₂—t₃期间，将励磁线圈的电流缓慢减小至0，在葫芦形回路中产生感应电流I₁，以维持磁通守恒。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 场冷励磁方法下REBCO闭环超导葫芦形环片堆叠磁体磁通密度放大原理

Fig. 5 Schematic diagram of magnetic flux amplification of REBCO closed-loop superconducting gourd-shaped loop stack magnet under field cooling method

1.3 基本方程

1.3.1 电磁场仿真模块的建立

计算超导电磁场的麦克斯韦方程组为

\{\begin{array}{l} \nabla \times E = - \partial B / \partial t \\ \nabla \times H = J \\ \nabla \cdot B = 0 \end{array}

(1)

超导的电磁本构方程为

\{\begin{array}{l} E = ρ J \\ B = μ_{0} μ_{r} H \end{array}

(2)

式中： $E$ 为电场强度，V/m； $B$ 为磁感应强度，T； $H$ 为磁场强度，A/m； $J$ 为电流密度，A/m²；t为时间，s； $ρ$ 为电阻率， $Ω \cdot m$ ； $μ_{0}$ 为真空磁导率，H/m； $μ_{r}$ 为相对磁导率，通常取1。

由式(1)、(2)可得基于 $H$ 方法的控制方程^[19]：

\nabla \times ρ (\nabla \times H) + μ \frac{\partial H}{\partial t} = 0

(3)

式中 $μ = μ_{0} μ_{r} = μ_{0}$ ，H/m。

写入有限元软件的偏微分方程模块中为

[\begin{matrix} 0 & E_{z} & - E_{y} \\ - E_{z} & 0 & E_{x} \\ E_{y} & - E_{x} & 0 \end{matrix}] + [\begin{matrix} μ_{0} & 0 & 0 \\ 0 & μ_{0} & 0 \\ 0 & 0 & μ_{0} \end{matrix}] \frac{\partial u}{\partial t} = [\begin{matrix} 0 \\ 0 \\ 0 \end{matrix}]

(4)

式中： $u = H = [\begin{matrix} H_{x} & H_{y} & H_{z} \end{matrix}]$ ， $H_{x}$ 、 $H_{y}$ 和 $H_{z}$ 分别为磁场强度在x、y和z轴上的分量，A/m； $E_{x}$ 、 $E_{y}$ 和 $E_{z}$ 分别为电场强度在x、y和z轴上的分量，V/m。

超导区域的电阻率采用非线性的幂指数函数(E-J定律)来描述超导体的电压电流特性，E-J定律可以得到区别于正常金属线性电阻率的超导体等效电阻，即

ρ = \frac{E_{c}}{J_{c} (B)} \cdot {[\frac{|J|}{J_{c} (B)}]}^{n}

(5)

式中： $E_{c} = 10^{- 4} V / m$ ，为临界电场强度；n=21，为77 K温度下的实验数据拟合的蠕动系数； $J_{c} (B)$ 为临界电流密度，A/m²。

$J_{c} (B)$ 是与磁场密切相关的物理量，这里用经验公式Kim模型来描述这二者间的关系：

J_{c} (B) = J_{c 0} {(1 + \frac{\sqrt[]{k^{2} B_{∥}^{2} + B_{⊥}^{2}}}{B_{0}})}^{- α}

(6)

式中： $J_{c 0}$ 为初始临界电流密度，A/m²； $B_{∥}$ 和 $B_{⊥}$ 分别为磁通密度 $B$ 相对于葫芦形环路的平行分量和垂直分量，T； $B_{0}$ 为受温度影响的宏观归一化参数；k和α为拟合参数。本文k、 $B_{0}$ 和α分别设定为0.25、20 mT和0.65。

1.3.2 固体力学模块的建立

假设环片的力学响应为准静态，因此不考虑惯性项的平衡方程为 $\nabla \cdot σ + F = 0$ ， σ 为应力， $F$ 为磁体受到的单位体积电磁力，在电磁环境下的磁体承受的单位体积电磁力与其内部磁通涡旋线受到的洛伦兹力大小相等。在此模型中 $F$ 表示为

F = [\begin{array}{l} f_{x} \\ f_{y} \\ f_{z} \end{array}] = [\begin{array}{l} J_{y} B_{z} - J_{z} B_{y} \\ J_{z} B_{x} - J_{x} B_{z} \\ J_{x} B_{y} - J_{y} B_{x} \end{array}]

(7)

式中： $J_{x}$ 、 $J_{y}$ 和 $J_{z}$ 分别为 $x$ 、 $y$ 和 $z$ 方向的电流密度，A/m²； $B_{x}$ 、 $B_{y}$ 和 $B_{z}$ 分别为 $x$ 、 $y$ 和 $z$ 方向的磁感应强度，T。本文主要涉及电磁应力，热应力、预应力等因素暂未考虑在内。

运用弹性力学基本方程来处理电磁应力的问题，平衡方程得到应力分量和单位体积电磁力分量的关系式^[20]如下：

\{\begin{array}{l} \frac{\partial σ_{x}}{\partial x} + \frac{\partial τ_{x y}}{\partial y} + \frac{\partial τ_{x z}}{\partial z} + f_{x} = 0 \\ \frac{\partial σ_{y}}{\partial y} + \frac{\partial τ_{x y}}{\partial x} + \frac{\partial τ_{y z}}{\partial z} + f_{y} = 0 \\ \frac{\partial σ_{z}}{\partial z} + \frac{\partial τ_{x z}}{\partial x} + \frac{\partial τ_{y z}}{\partial y} + f_{z} = 0 \end{array}

(8)

式中： $σ_{x}$ 、 $σ_{y}$ 、 $σ_{z}$ 、 $τ_{x y}$ 、 $τ_{y z}$ 和 $τ_{x z}$ 分别为 $x$ 、 $y$ 、 $z$ 、 $x y$ 、 $y z$ 和 $x z$ 方向的应力，Pa。

微元体线段上的应变分量与位移分量之间的关系如下：

\{\begin{array}{l} ε_{x} = \frac{\partial u}{\partial x} \\ ε_{y} = \frac{\partial v}{\partial y} \\ ε_{z} = \frac{\partial w}{\partial z} \\ γ_{x y} = \frac{\partial v}{\partial x} + \frac{\partial u}{\partial y} \\ γ_{y z} = \frac{\partial w}{\partial y} + \frac{\partial v}{\partial z} \\ γ_{z x} = \frac{\partial u}{\partial z} + \frac{\partial w}{\partial x} \end{array}

(9)

式中： $ε_{x}$ 、 $ε_{y}$ 、 $ε_{z}$ 、 $γ_{x y}$ 、 $γ_{y z}$ 和 $γ_{x z}$ 分别为 $x$ 、 $y$ 、 $z$ 、 $x y$ 、 $y z$ 和 $x z$ 方向的应变； $u$ 、 $v$ 和 $w$ 分别为沿 $x$ 、 $y$ 和 $z$ 方向的位移，m。

应变分量与应力分量之间的物理关系式如下：

\{\begin{array}{l} ε_{x} = [σ_{x} - λ (σ_{y} + σ_{z})] / E \\ ε_{y} = [σ_{y} - λ (σ_{x} + σ_{z})] / E \\ ε_{z} = [σ_{z} - λ (σ_{x} + σ_{y})] / E \\ γ_{x y} = \frac{2 (1 + λ)}{E} τ_{x y} \\ γ_{y z} = \frac{2 (1 + λ)}{E} τ_{y z} \\ γ_{z x} = \frac{2 (1 + λ)}{E} τ_{z x} \end{array}

(10)

式中： $E$ 为材料的杨氏模量，Pa；λ为材料的泊松比； $G = E / 2 / (1 + λ)$ 是剪切模量，又称刚度模量，Pa。本文中REBCO超导带材的 $E$ 和λ分别设定为228 GPa和0.307^[21]。

2 仿真结果与分析

2.1 磁体的电流密度分布、磁场分布

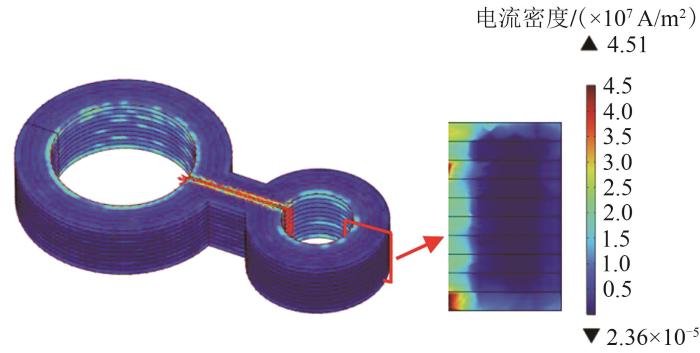
励磁结束后，葫芦形回路中产生感应电流I₁，以维持磁通守恒。励磁完成后葫芦形堆叠磁体的电流密度分布云图如图6所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 励磁完成后葫芦形堆叠磁体的电流密度分布云图

Fig. 6 Current density distribution cloud diagram of gourd-shaped stacked magnets after excitation

从图6中可以看到，电流沿着大圆、小圆的内径到外径逐渐减小，连接桥部分的电流密度明显大于圆环部分，这是由于连接桥部分宽度小于环宽，所以电流密度会增加。励磁完成后葫芦形堆叠磁体的磁场分布云图如图7所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

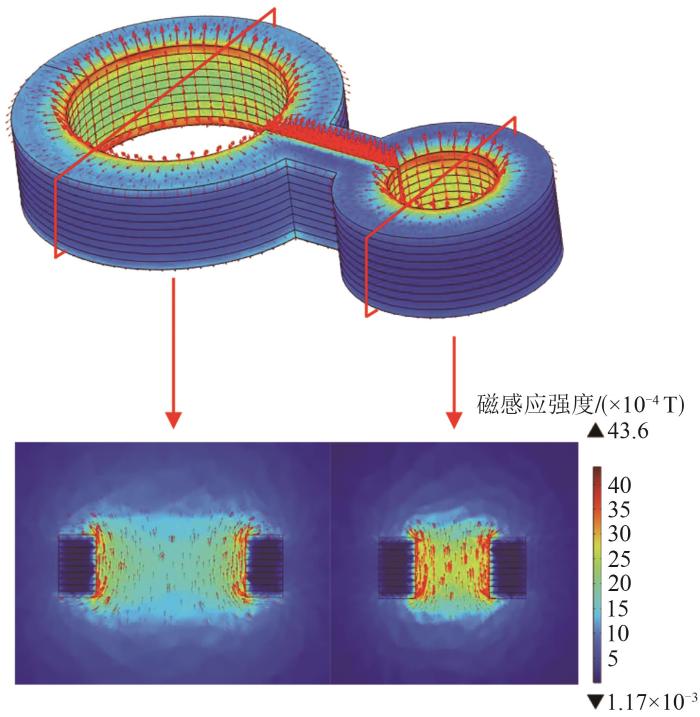
图7 励磁完成后葫芦形堆叠磁体的磁场分布云图

Fig. 7 Magnetic field distribution cloud diagram of gourd-shaped stacked magnets after excitation

要计算单位体积电磁力 $F = J \times B$ ，需知道环片上的电流密度分布和磁场分布，由于葫芦形环片具有对称性，因此可以在柱坐标下求得大圆、小圆一个径向上的单位体积电磁力分布，柱坐标下求解单位体积电磁力示意图如图8所示。将磁场分解为平行磁场和垂直磁场，由于磁场与电流密度垂直，易得到磁体的径向单位体积电磁力和轴向单位体积电磁力。仿真得到葫芦形堆叠磁体沿径向的单位体积电磁力分布如图9所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

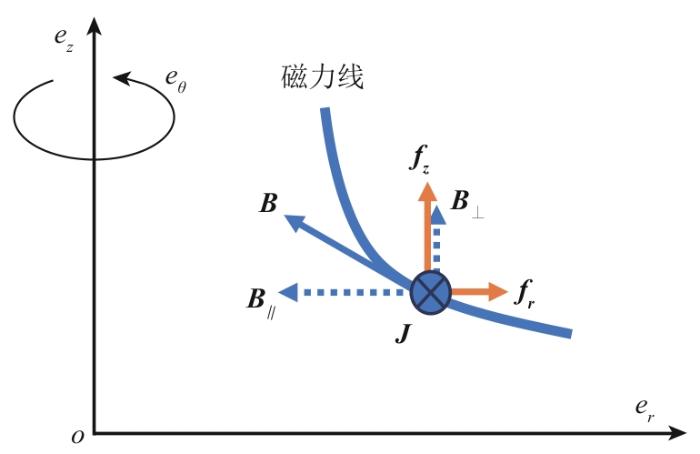
图8 柱坐标下求解单位体积电磁力示意图

Fig. 8 Schematic diagram of solving unit volume electromagnetic force in cylindrical coordinates

图9

新窗口打开| 下载原图ZIP| 生成PPT

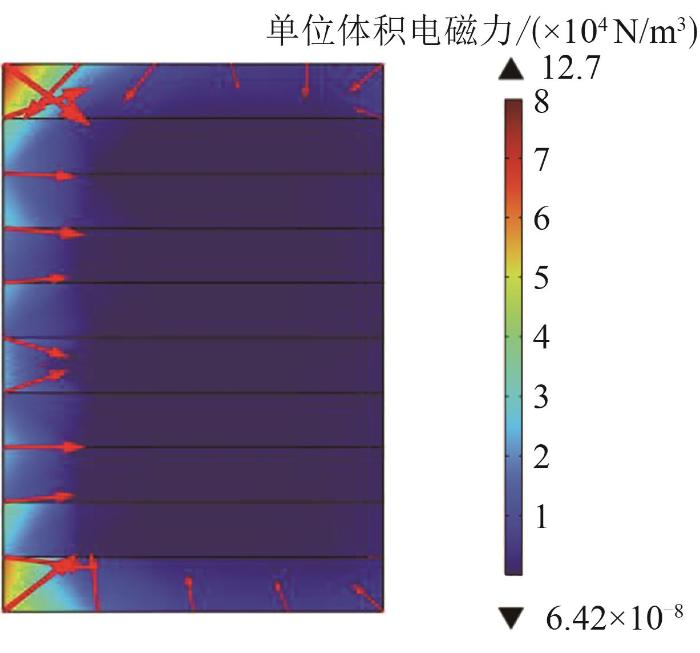
图9 励磁完成后葫芦形堆叠磁体沿径向的单位体积电磁力分布云图

Fig. 9 Cloud diagram of the unit volume electromagnetic force distribution along the radial direction of the gourd-shaped stacked magnet after excitation

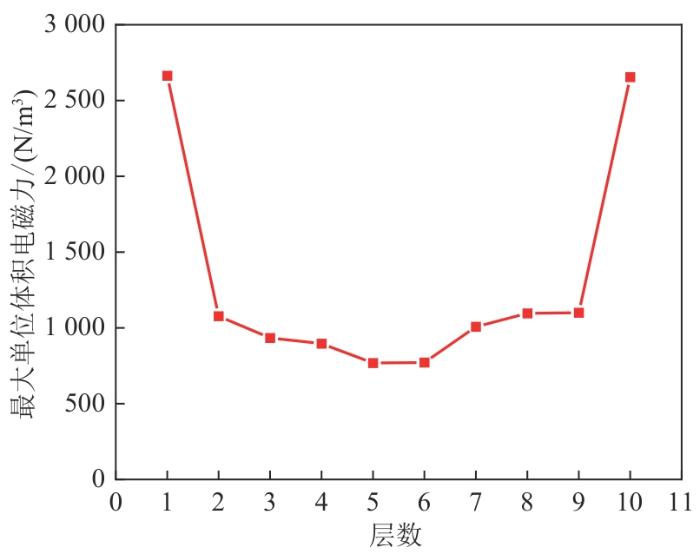
以葫芦形堆叠磁体的底部为第1层，依次编号为第2，3，…，10层。第1层和第10层的单位体积电磁力的最大值最大，高达2 664 N/m³，两端向中部逐渐减小，第5、6层单位体积电磁力的最大值最小，低至767.96 N/m³。

第2层相对于第1层的最大单位体积电磁力降低了59.55%。这是因为第1层葫芦形环片具有更大的磁场分布和电流密度分布。因此，在这种葫芦形堆叠磁体中，顶部和底部内侧有力的集中。每一层的最大单位体积电磁力大小如图10所示。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 每一层的最大单位体积电磁力大小

Fig. 10 The maximum unit volume electromagnetic force of each layer

2.2 磁体的应力应变分析

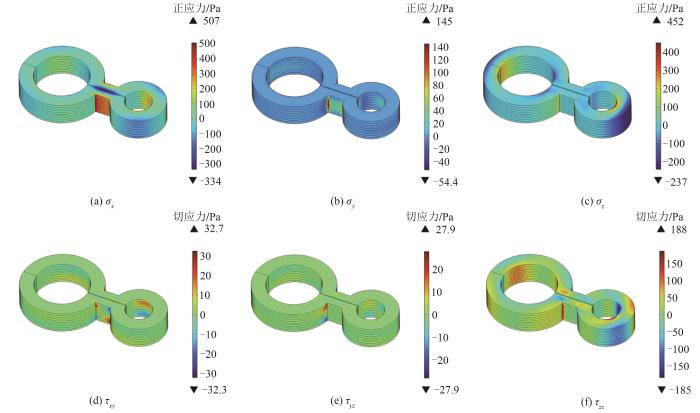
求得磁体的单位体积电磁力后，由平衡方程、几何方程和本构方程得到葫芦形堆叠磁体的正应力和切应力分布，如图11所示。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 葫芦形堆叠磁体的正应力、切应力分布云图

Fig. 11 Normal stress and shear stress distribution cloud diagram of gourd-shaped stacked magnets

总体来看，应力在磁体的连接桥部位以及圆孔与桥的交点处(弯曲较多的区域)明显较大，这些区域应力较集中，是可能失超的潜在风险点。2个圆环的应力分布集中在圆环的内径和两端，相对桥区域较均匀。

定量来看，x方向正应力和z方向正应力较大，最大值分别高达507 Pa和452 Pa，这是由于在这2个方向上的体载荷相对较重，沿y方向应力分量较小，只有145 Pa。zx平面的剪切应力较大，最大值有188 Pa，表明环片在zx平面上经历了较大的扭转作用力，xy和yz平面的剪切应力较小，因此磁体在这2个方向上扭转的程度较小。

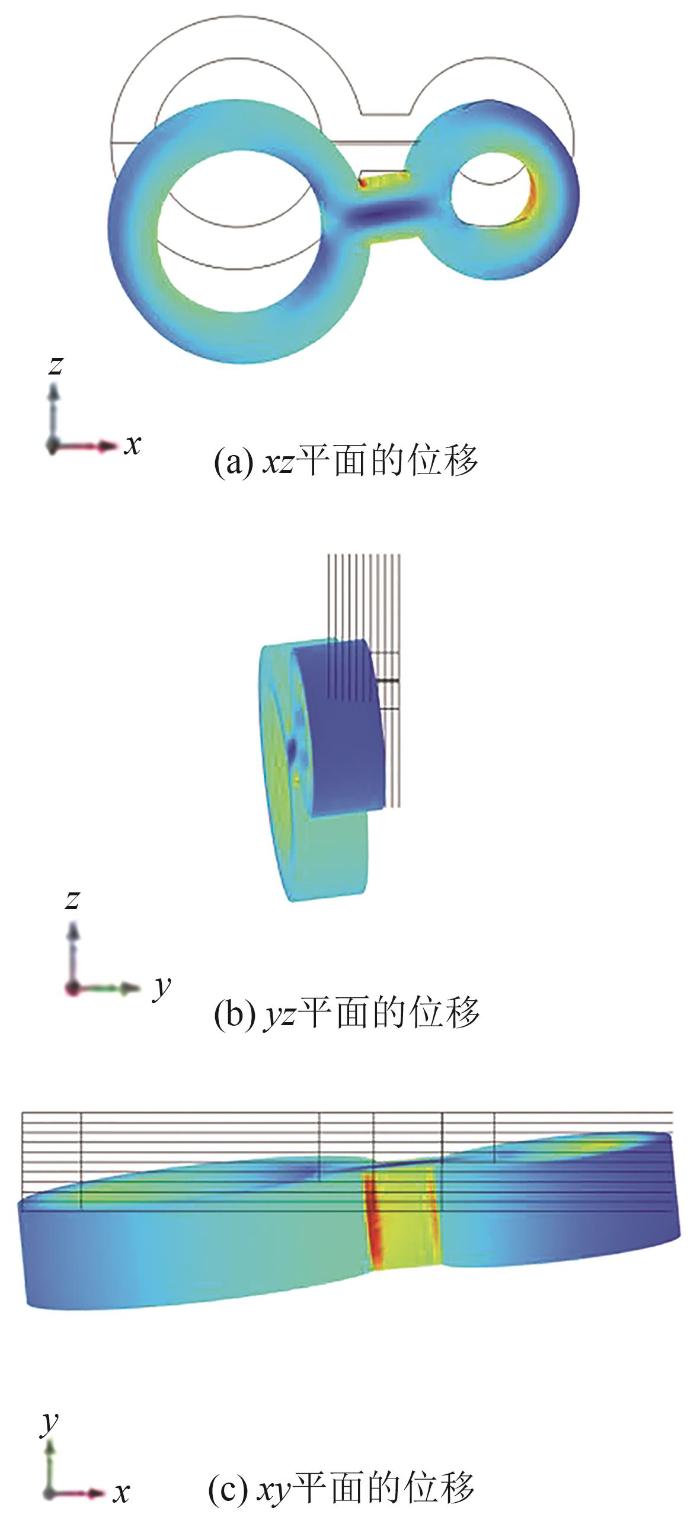
为了能明显观察到REBCO闭环超导葫芦形环片堆叠磁体的扭转和位移，将其位移放大了100倍，得到沿x、y、z方向的位移如图12所示。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 葫芦形堆叠磁体的位移变化图

Fig. 12 Displacement variation diagram of gourd-shaped stacked magnets

由图12可以看到，大圆圆环相对于小圆圆环沿z方向的位移更大；葫芦形堆叠磁体整体以桥为轴，相对于zx平面扭转程度较大，且环片整体沿z方向下移，沿y方向下有一定位移，与它受到的应力产生的效果一致。因此，在实际使用中要考虑应力应变因素对磁体产生的影响。

3 结论

给出了计算REBCO闭环超导葫芦形环片堆叠磁体的电磁场分布的H方法控制方程及其有限元离散格式。基于该方法，构建了REBCO闭环超导葫芦形环片堆叠磁体的三维电磁力模型，该模型通过场冷励磁方法对磁体励磁，得到了电流密度分布、磁场分布和单位体积电磁力分布，其各个方向的应力张量和应变张量，以及受电磁应力后磁体的位移变形情况。得到以下结论：

1）REBCO闭环超导葫芦形环片堆叠磁体的单位体积电磁力由圆环的内径向外径逐渐减小，最大单位体积电磁力在堆叠磁体的两端层数较高，而中间层数则显著降低，最大单位体积电磁力随层数变化的趋势呈现明显的“U”型分布特征。

2）REBCO闭环超导葫芦形环片堆叠磁体的应力在磁体的连接桥部位以及圆孔与桥的交点处(弯曲较多的区域)明显较大，这些区域应力较集中，受力情况差，易发生形变，是可能失超的潜在风险处。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

LEE

， PARK

， MICHAEL

P C

，et al ．

A field-shaking system to reduce the screening-current-induced field in the 800-MHz HTS insert of the MIT 1.3-GHz LTS/HTS NMR magnet：a small-model study

[J]．IEEE Transactions on Applied Superconductivity，2018，28(3)：1-5． doi:10.1109/tasc.2018.2803801