聚变装置高温超导磁体系统电磁仿真方法研究

doi:10.12096/j.2096-4528.pgt.24128

聚变装置高温超导磁体系统电磁仿真方法研究

徐浩睿¹^,², 王苏鑫¹^,², 李留江¹^,², 严植泳¹^,², 谭运飞¹^,²

1.强电磁工程与新技术国家重点实验室（华中科技大学电气与电子工程学院），湖北省武汉市 430074

2.华中科技大学国家脉冲强磁场科学中心，湖北省武汉市 430074

Research on Electromagnetic Simulation Method of Fusion High-Temperature Superconducting Magnet System

XU Haorui¹^,², WANG Suxin¹^,², LI Liujiang¹^,², YAN Zhiyong¹^,², TAN Yunfei¹^,²

1.State Key Laboratory of Advanced Electromagnetic Engineering and Technology (School of Electrical and Electronic Engineering, Huazhong University of Science and Technology), Wuhan 430074, Hubei Province, China

2.Wuhan National High Magnetic Field Center, Huazhong University of Science and Technology, Wuhan 430074, Hubei Province, China

收稿日期: 2024-07-21 修回日期: 2024-08-22

基金资助:

国家磁约束核聚变能发展研究专项. 2022YFE03150104
国家电网有限公司科技项目. 5500-202355837A-4-3-WL

Received: 2024-07-21 Revised: 2024-08-22

作者简介 About authors

徐浩睿(2002)，男，硕士研究生，主要研究方向为聚变高温超导磁体的设计与分析，941584026@qq.com；

王苏鑫(2001)，男，博士研究生，主要研究方向为聚变超导磁体的设计与分析，d202380856@hust.edu.cn；

李留江(1997)，男，博士研究生，主要研究方向为高温超导体的失超传播特性，d202380876@hust.edu.cn；

严植泳(1997)，男，博士研究生，主要研究方向为应用超导技术，yanzy15@tsinghua.org.cn；

谭运飞(1980)，男，博士，研究员，长期从事稳态强磁场装置的设计和研发，本文通信作者，tanyf@hust.edu.cn。

摘要

目的高温超导磁体系统的应用是未来托卡马克装置的重要技术路线，然而高温超导带材的磁场各向异性以及复杂的导体结构极大地增加了聚变装置高温超导磁体系统电磁设计阶段仿真模拟的复杂度，因此需要针对其电磁仿真以及简化方法开展相应研究。方法通过有限元仿真软件COMSOL建立高温超导磁体系统总体电磁仿真模型与各种简化模型，对其相关电磁性能进行了仿真分析与对比。结果等离子体区域中心磁场与最大波纹度的计算结果主要受纵场(toroidal field，TF)线圈产生的磁场控制，而TF线圈对中心螺线管(central solenoid，CS)线圈上的磁场分布影响很小。当结合导体的详细结构并考虑高温超导带材的磁场各向异性时，垂直磁场的计算结果与总体模型相比具有较大差异。结论在等离子体区域内的相关电磁参数的计算上可以仅考虑TF线圈，而在分析CS线圈上磁场时可忽略TF线圈。此外，通过结合导体结构的平均电流分布，可以有效降低高温超导带材垂直磁场的仿真计算误差。

关键词： 核聚变 ; 聚变发电 ; 托卡马克磁体系统 ; 高温超导磁体 ; 电磁分析 ; 模型对比

Abstract

Objectives The application of high-temperature superconductivity (HTS) magnet system is an important technical route for future tokamak devices. However, the magnetic field anisotropy of the HTS tape and the complex conductor structures greatly increase the complexity of the simulation in the electromagnetic design stage of the HTS magnet system of the fusion device. It is necessary to carry out the corresponding research on the electromagnetic simulation and simplified methods. Methods The finite element simulation software COMSOL was used to establish the overall electromagnetic simulation model and various simplified models of the HTS magnet system, and the related electromagnetic properties were simulated and compared. Results The calculation results of the central magnetic field and the maximum ripple of plasma are mainly controlled by the magnetic field generated by the toroidal field (TF) coil. However, the TF coil has little influence on the magnetic field distribution on the central solenoid (CS) coil. When the detailed structure of the conductor is combined and the magnetic field anisotropy of the HTS tape is considered, the calculated results of the vertical magnetic field show a large difference compared with the overall model. Conclusions The TF coil can only be considered in the calculation of the relevant electromagnetic parameters in the plasma region, and the TF coil can be ignored in the analysis of the magnetic field on the CS coil. In addition, by combining the average current distribution of the conductor structure, the simulation error of the vertical magnetic field of the HTS tape can be effectively reduced.

Keywords： nuclear fusion ; fusion power ; tokamak magnet system ; high-temperature superconductivity ; electromagnetic analysis ; model comparison

PDF (6222KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

徐浩睿, 王苏鑫, 李留江, 严植泳, 谭运飞. 聚变装置高温超导磁体系统电磁仿真方法研究. 发电技术[J], 2024, 45(6): 1030-1038 DOI:10.12096/j.2096-4528.pgt.24128

XU Haorui, WANG Suxin, LI Liujiang, YAN Zhiyong, TAN Yunfei. Research on Electromagnetic Simulation Method of Fusion High-Temperature Superconducting Magnet System. Power Generation Technology[J], 2024, 45(6): 1030-1038 DOI:10.12096/j.2096-4528.pgt.24128

0 引言

托卡马克作为磁约束核聚变中最有可能率先实现聚变发电的技术路线，自20世纪50年代被苏联科学家提出以后，科研人员对其持续开展研究。托卡马克的磁体系统作为产生磁场以及形成、约束等离子体的最关键部件，其主要包括纵场(toroidal field，TF)磁体、中心螺线管(central solenoid，CS)磁体以及极向场(poloidal field，PF)磁体等，需要在托卡马克装置的建设过程中对其进行详细设计与仿真模拟。早期的托卡马克装置采用常规的铜磁体，由于铜磁体在通入千安级别的电流时会产生大量的热，严重时甚至会导致磁体烧毁，因此铜磁体托卡马克装置只能以极短脉冲的方式运行，严重限制了托卡马克装置的性能。与常规铜导体相比，超导体在特定条件下电阻率非常小，载流性能好，可以有效改善托卡马克装置的运行时间，实现长脉冲稳态运行^[1]。国际热核聚变反应堆装置(international thermonuclear experimental reactor，ITER)是目前国际上合作的最大规模的超导托卡马克装置，其导体材料主要采用低温超导材料NbTi、Nb₃Sn^[2]。此外，国际上多国建造的示范反应堆(demonstration reactor，DEMO)也采用了同样的低温超导磁体路线，如中国聚变工程实验堆(China fusion engineering test reactor，CFETR)^[3]、韩国的K-DEMO^[4]、欧洲的EU-DEMO^[5]、日本的JA-DEMO^[6]等。

近年来，高温超导技术为托卡马克装置的发展带来了新机遇。相比于低温超导材料，高温超导材料在相同工作条件下具有更高的电流密度和临界磁场强度，有利于建造更紧凑、具有更高磁场强度的聚变装置。国际上，美国麻省理工学院(Massachusetts Institute of Technology，MIT)联合联邦核聚变系统(Commonwealth Fusion Systems，CFS)公司，正在设计建造基于高温超导材料稀土钡铜氧(rare earth barium copper oxide，REBCO)的紧凑聚变反应堆(sooner/smaller privately-funded affordable-robust-compact，SPARC)装置。目前，该团队已完成了最高磁场强度达到20 T的TF模型线圈的设计、制造与测试工作^[7]。国内，能量奇点公司完成了首个全高温超导托卡马克装置的建设并成功实现了等离子体放电。这些工作均初步验证了高温超导磁体在托卡马克装置中应用的可行性^[8]。

不同于低温超导带材的线性结构，二代高温超导材料是具有很大宽厚比的带材结构，其载流能力会受磁场方向、应力等因素的影响。目前，已有多种基于二代高温超导带材REBCO的管内电缆导体(cable-in-conduit conductor，CICC)结构被提出，如Roeble^[9]、圆芯电缆(conductor on round core，CORC)^[10]、扭绞堆叠电缆(twisted stacked-tapes cable，TSTC)^[11]、准各向同性股线(quasi-isotropic strand，Q-IS)^[12]。这些导体均采用了扭绞换位的形式，以降低其运行过程中的交流损耗，但超导带材的扭转降低了导体的机械性能，并带来了复杂的制造工艺。

超导托卡马克装置的磁体运行电流很高，运行时的磁场很强，这对大型磁体系统及其导体的结构、制造工艺都提出了较高的要求，同时聚变装置等离子体的性能也与磁体产生的磁场密不可分，所以超导磁体的电磁仿真分析是托卡马克磁体系统设计的重要工作之一。目前，国内外对聚变磁体系统的电磁仿真方法大多基于低温超导磁体结构^[13-15]，然而高温超导带材具有较强的磁场各向异性，且具有与低温超导CICC完全不同的导体结构，因此需要针对聚变装置高温超导磁体，结合其CICC结构的电磁仿真方法开展相应研究。为此，本文在COMSOL有限元软件中对聚变装置高温超导磁体系统进行搭建，分析空间中磁场分布情况并对相关电磁参数进行对比分析。

1 电磁仿真原理及计算模型

1.1 理论基础

本文所涉及的基本原理主要基于麦克斯韦方程组，该方程组阐释了电场、磁场与电流密度、电荷密度之间的联系^[16]。它包含积分和微分2种形式，在计算电磁场问题中通常使用麦克斯韦方程组的微分形式进行求解。

电场的高斯定理为

\nabla \cdot D = ρ

(1)

式中： D 为电通量密度；ρ为电荷密度。

电磁感应定律为

\nabla \times E = - \frac{\partial B}{\partial t}

(2)

式中： E 为电场强度； B 为磁感应强度。

全电流定律为

\nabla \times H = J + \frac{\partial D}{\partial t}

(3)

式中： H 为磁场强度； J 为电流密度。

磁场中的高斯定理为

\nabla \cdot B = 0

(4)

超导体与常规导体在分析计算时最大的区别是电场强度与电流密度的关系。与常规导体不同，超导体电场强度值与电流密度值呈n次幂关系：

E = E_{0} (J / J_{C})^{n}

(5)

式中：E₀为常数，一般取值10^-4 V/m；J_C为临界电流密度。n与材料、温度有关，通常取值10~100。n=1时，表明超导体具有线性电阻特性，与常导体无异；n=∞时，则表明超导体的电磁特性符合Bean模型^[17]。

考虑到超导体的非线性E-J关系和托卡马克装置超导磁体系统的复杂结构带来的巨大计算量，在电磁仿真时通常采用平均电流分布对超导磁体的截面电流密度进行简化。

1.2 计算模型与模块

本文使用COMSOL Multiphysics有限元仿真软件^[18]对聚变装置高温超导磁体系统进行搭建与分析，超导磁体系统主要参数如表1所示，其物理参数设计来自目前最先进的高温超导托卡马克装置SPARC^[19-21]。计算模型中包含16个TF线圈、8个PF线圈及6个CS线圈，线圈所采用的材料为第二代高温超导材料。磁体系统环向截面图如图1所示，其中CS1U、CS2U、CS3U为自下而上排布的CS线圈；PF1U、PF2U、PF3U、PF4U为自内而外排布的PF线圈。托卡马克磁体系统整体计算模型结构如图2所示。

表1 超导磁体系统主要参数

Tab. 1 Main parameters of superconducting magnet system

参数	数值
中心磁感应强度B_t/T	12
大半径R/m	1.85
小半径a/m	0.57
波纹度δ/%	<0.5

新窗口打开| 下载CSV

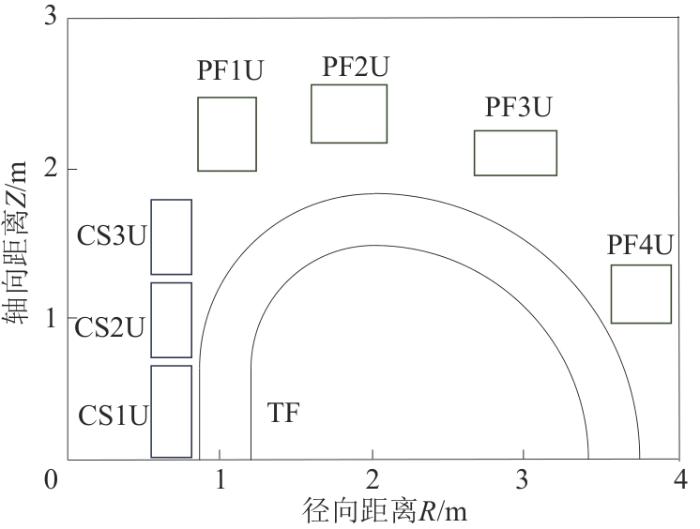
图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 磁体系统环向截面图

Fig. 1 Cross-section of magnet system

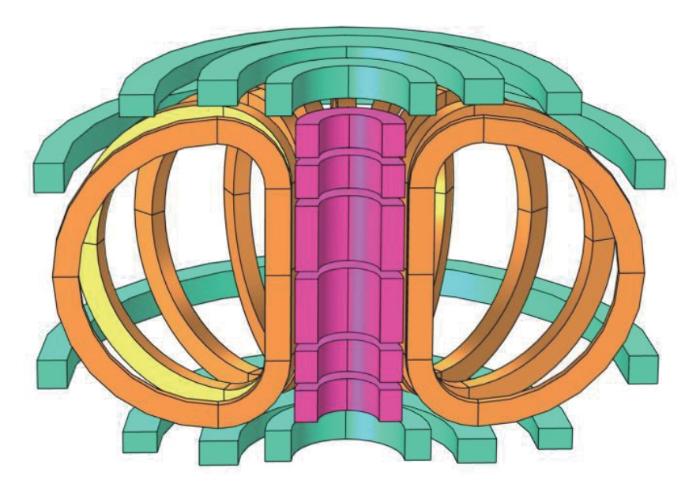
图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 磁体系统计算模型结构

Fig. 2 Calculation model structure of magnet system

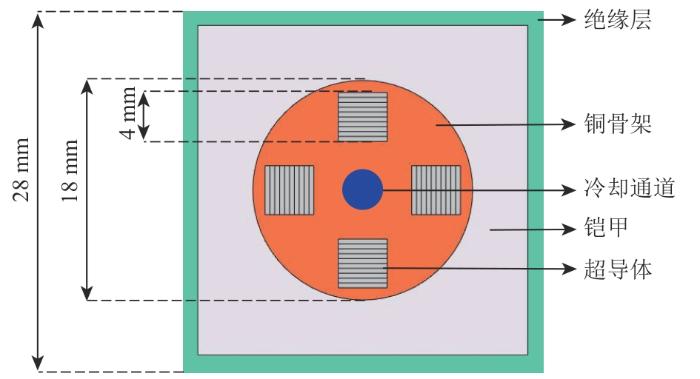
本文分析重点在于获取空间中磁场分布情况，同时在稳态情况下对空间中磁场进行计算与分析。计算模型采用的模块为COMSOL软件中内置的磁场模块。考虑到磁体系统在空间中具有环向周期性分布的特点，通过在三维模型仿真分析中截取磁体系统的1/16部分，并在模型边界分别设置磁场模块中自带的理想磁导体(磁场垂直于相应边界)和磁绝缘(磁场平行于相应边界)边界条件进行仿真计算，可以极大程度上减少计算量，节省计算时间。本文采用的CICC结构为四沟槽简单堆叠的无扭转导体，具体结构如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 导体结构图

Fig. 3 Conductor structure

2 磁体系统的整体三维电磁分析

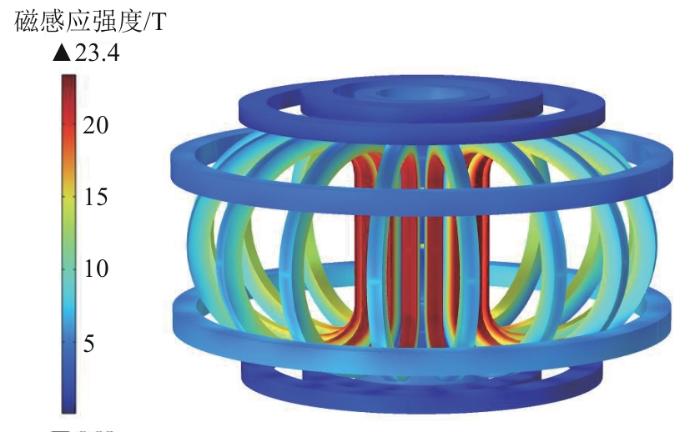
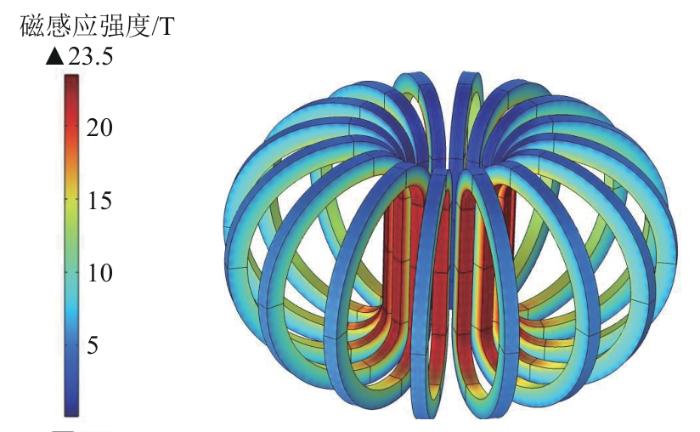
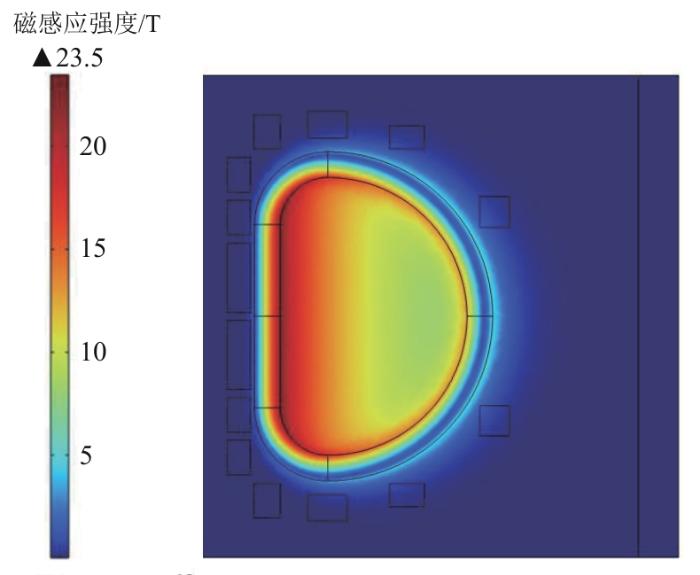
通过对磁体系统的整体三维电磁分析，研究线圈内部和等离子体区域的磁场分布情况。为了减少计算量、降低计算难度，在三维模型中未考虑各个线圈的详细导体结构。通过对线圈截面设置平均电流分布，并对各部分线圈施加相应的电流驱动，可得到整个磁体系统上的磁场分布情况，具体如图4所示。可以看出，磁场主要集中在TF线圈直线段，最高磁感应强度达到23.4 T；CS线圈最高磁感应强度为16.1 T；PF线圈最高磁感应强度为7.34 T。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 磁体系统磁场分布图

Fig. 4 Magnetic field distribution of magnet system

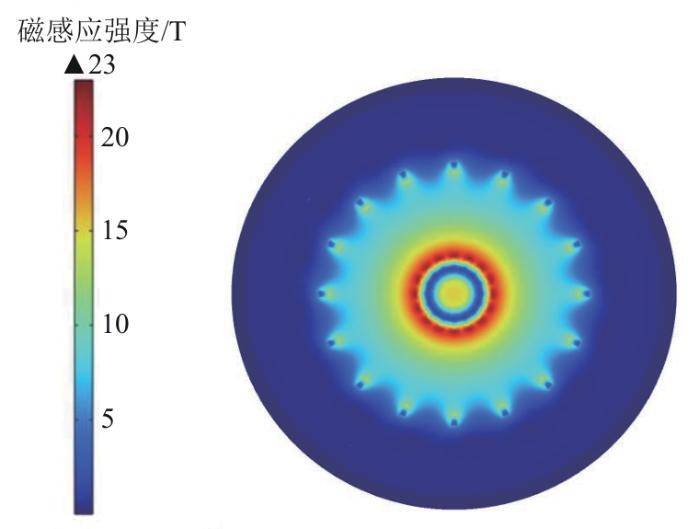
图5展示了赤道平面磁场分布情况，在等离子体中心(R=1.85 m)产生的磁感应强度为12.16 T，总体呈现出由内而外磁感应强度逐渐减小的趋势，且由于TF线圈的周期性分布，其在环向上产生的磁场也存在起伏波动的情况。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 整体模型赤道平面磁场分布图

Fig. 5 Magnetic field distribution of system model in the equatorial plane

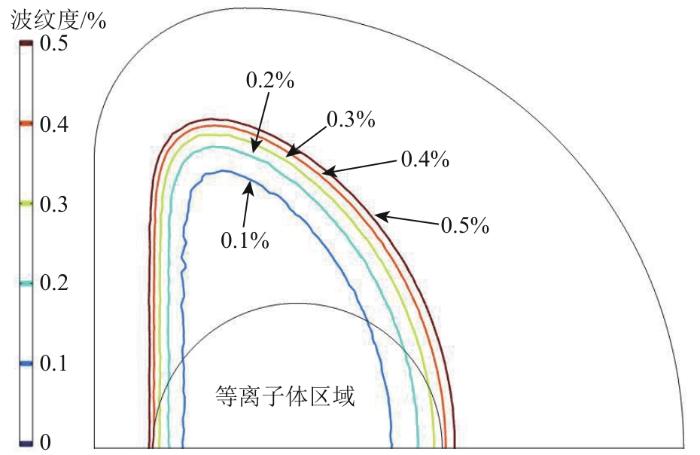
波纹度被用来定义等离子体区域的磁场均匀程度，其大小直接影响等离子体的约束性能，波纹度越小，对等离子体的约束性能越好，具体表达式如下：

δ (R, Z) = \frac{B_{τ m a x} - B_{τ m i n}}{B_{τ m a x} + B_{τ m i n}}

(6)

式中 $B_{τ m a x}$ 、 $B_{τ m i n}$ 分别表示在径向距离R和轴向距离Z确定以后，整个圆环路径上磁感应强度的最大、最小值。

从图5可以看出， $B_{τ m a x}$ 位于TF线圈1/2厚度的中平面上， $B_{τ m i n}$ 位于2个相邻线圈1/2缝隙的中平面上。

对2个截面上的磁场进行相应的处理，即可得到等离子体区域的波纹度，具体如图6所示。等离子体区域近似为一个圆形区域(R=1.28~2.42 m)，从等离子体区域与波纹度曲线交会情况可以看出，其区域范围内的最大波纹度约为0.4%。总体来说，通过电磁分析得到的中心磁场和波纹度都较好地满足了目前托卡马克装置对等离子体区域磁场分布的要求^[22]。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 等离子体区域波纹度分布

Fig. 6 Ripple distribution of plasma

3 仿真简化分析

计算模型中同时考虑3种类型的线圈，会给仿真带来较大的计算量，不利于结合具体的CICC结构进行详细的仿真分析，因此本文对托卡马克磁体系统电磁仿真的简化方法进行研究。TF线圈与CS、PF线圈由于通入的电流方向不同，进而导致产生的磁场方向和分布位置不同，因此可以将这3种类型的线圈分为2组进行单独分析：一是将TF线圈归为一类，单独对其进行电磁分析，计算等离子体区域的中心磁场与波纹度；二是将PF与CS线圈归为一类，计算线圈上的磁场分布情况。

3.1 TF线圈电磁分析

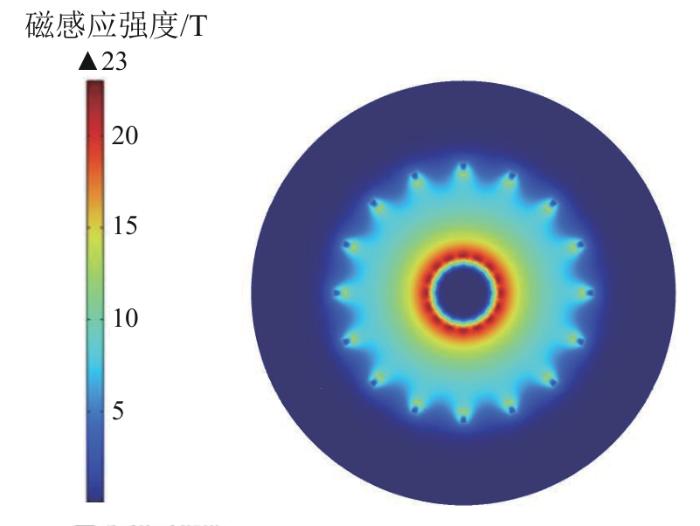
第一类简化模型忽略了CS和PF线圈，仅对TF线圈进行建模分析，所添加的电流驱动与整体分析时相同，由此得到空间中磁场分布情况并对其进行分析。图7展示了TF线圈内部的磁场分布情况。TF线圈的最大磁感应强度为23.5 T，与第2节所提到的23.4 T几乎一致。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 TF线圈磁场分布图

Fig. 7 Magnetic field distribution of TF coil

赤道平面的磁场分布如图8所示。对比图5可以看出，2个模型磁场的数值与分布趋势基本一致，只是整体模型在中心区域考虑了CS线圈的影响后，会出现接近15 T的磁场分布，而只考虑TF线圈的简化模型在此处的磁感应强度接近于0；所关注的等离子区域并未受到影响，简化模型的中心磁感应强度为12.11 T，与整体模型的中心磁感应强度12.16 T相比，误差仅为0.4%。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 TF线圈模型赤道平面磁场分布图

Fig. 8 Magnetic field distribution of TF coil model in the equatorial plane

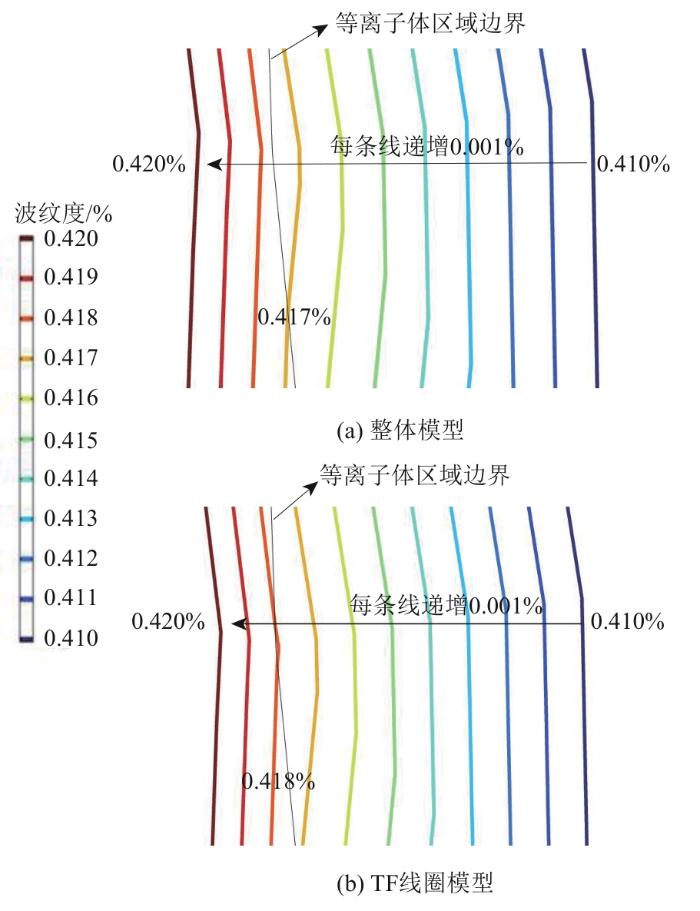
在简化模型中，等离子体区域的波纹度为0.4%，与磁体系统整体模型的计算结果相同，为了体现出两者的区别，图9展示了2个模型放大后的波纹度曲线。与整体模型相比，未考虑CS与PF线圈影响时，等离子体边界的最大波纹度仅从0.417%上升为0.418%。从波纹度的定义式(6)来看：由于CS与PF线圈产生的磁场具有环向对称性，其产生的磁场并不会造成环向磁场的差值变大，而当忽略PF与CS线圈产生的磁场时，在等离子体区域的总体磁场有所减小，导致波纹度变大。但总体来说，波纹度的改变非常小，几乎可以忽略不计。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 放大的波纹度曲线

Fig. 9 Magnified ripple curves

由上述对比结果可知，将PF、CS线圈忽略，对TF线圈内的磁场以及等离子体区域的中心磁场、波纹度的计算结果影响不大，验证了采用此种简化方法的可行性。

3.2 CS与PF线圈电磁分析

CS与PF线圈产生的磁场主要沿极向方向，环向分量为0，而TF线圈产生的环向磁场在其内侧很大，在CS与PF线圈的外侧很小，如图10所示。在磁感应强度较大的CS线圈处，TF线圈产生的最大磁感应强度仅为0.45 T，因此在考虑CS线圈上磁场分布时，可近似忽略TF线圈的影响，将CS与PF线圈模型简化为二维轴对称模型。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 TF线圈产生磁场截面图

Fig. 10 Magnetic field distribution generated by TF coil

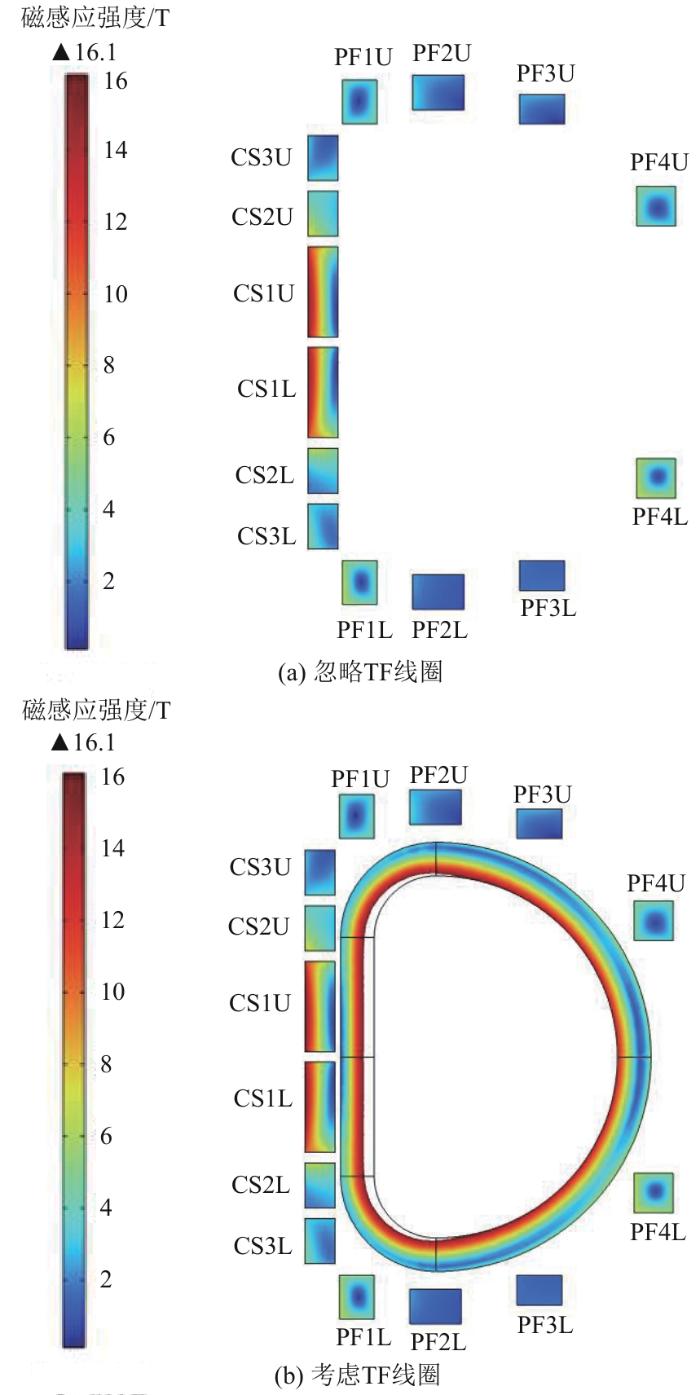
将考虑整个磁体的极向场线圈磁场分布图与不考虑TF线圈的极向场线圈磁场分布图进行对比，结果如图11所示，其中下半部分L线圈与上半部分U线圈关于径向对称。可以看出，TF线圈产生的磁场对PF4U和PF4L的边缘处会造成一定影响，而对CS线圈的影响几乎可以忽略不计。由此可见，忽略TF线圈的简化模型在CS与PF线圈上磁场总体的分布与整体模型基本一致。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 磁场分布环向截面图

Fig.11 Magnetic field distribution in poloidal field coil

4 结合CICC结构的极向场线圈电磁分析

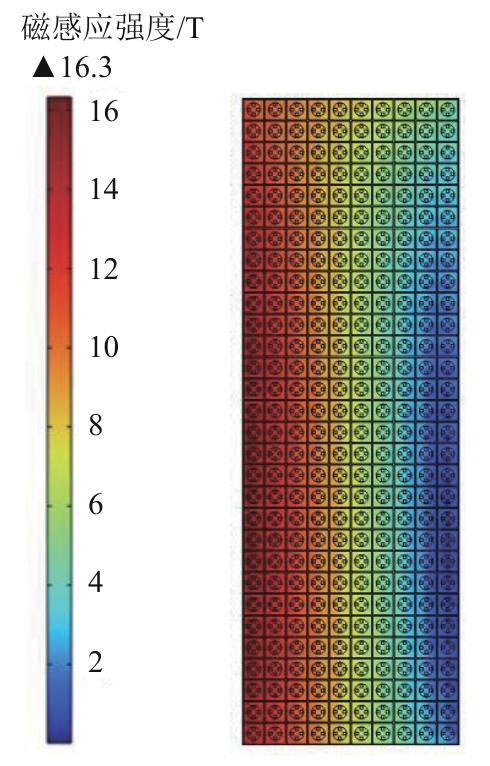
在实际运行过程中，CS与PF线圈处于快速励磁的状态，其运行电流会快速变化，且磁体系统的电磁计算结果显示，CS线圈会处于较大的背景磁场，因此为保证CS线圈有足够的运行安全裕量，确保仿真计算的准确性，需结合CICC的具体结构对磁体系统中的CS线圈进行详细电磁分析。

根据第3节的模型简化结果，为了进一步对CS线圈进行分析，本节的计算模型忽略了TF线圈，只考虑CS与PF线圈，并建立了对应的二维轴对称模型。其中，对通入电流较大、背景场最高的CS1U与CS1L线圈结合CICC结构(见图3)进行详细建模。在详细模型中，对堆叠超导带材和其余未详细建模的CS、PF线圈截面分别添加电流驱动，其在CS1U上产生的磁场如图12所示。其中磁感应强度最大值为16.3 T，这与三维模型下的CS线圈最大磁感应强度16.1 T相比，误差仅为1.24%，且磁场分布情况基本一致。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 CS1U磁场分布图

Fig. 12 Magnetic field distribution of CS1U

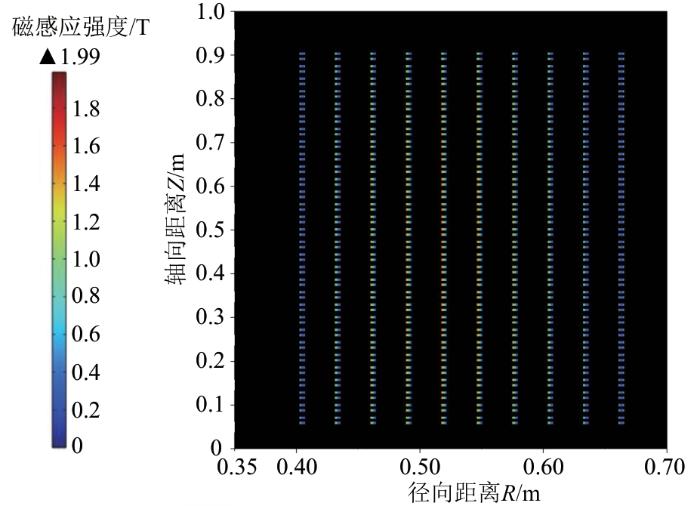
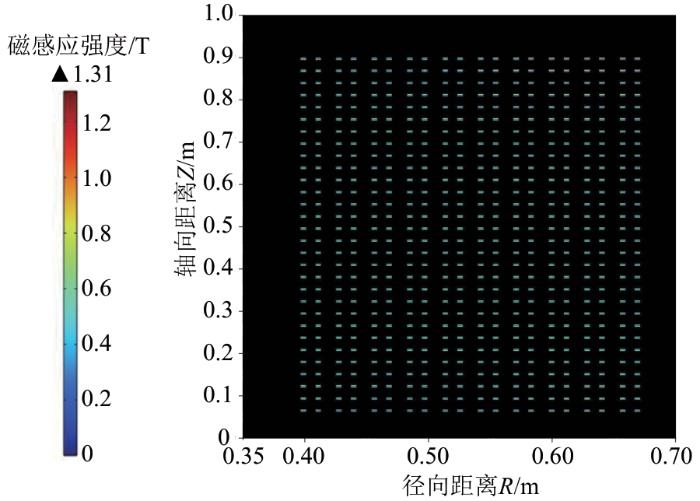
进一步，由于高温超导带材的临界性能有磁场各向异性的特点，且在垂直带材表面方向上临界电流衰减程度最大^[23]，针对高温超导带材临界电流的各向异性，本文对二维电磁仿真结果沿带材垂直方向进行分解。如图3所示，高温超导带材在竖直方向上下堆叠，垂直带材方向沿轴向；其在水平方向左右堆叠，垂直带材方向沿径向。对上下两部分导体的磁场沿轴向分解，左右两部分导体的磁场沿径向分解，并与未进行详细建模的二维模型相应位置的磁场分量进行对比。对于上下排布的高温超导带材，其详细模型中最大垂直磁感应强度为15.72 T，未详细建模的模型最大垂直磁感应强度为14.71 T，同一位置的垂直磁感应强度绝对误差最大可达到1.99 T，如图13所示。对于左右排布的高温超导带材，其详细模型中最大垂直磁感应强度为6.85 T，未详细建模的模型最大垂直磁感应强度为5.95 T，同一位置的垂直磁感应强度绝对误差最大可达到1.29 T，如图14所示。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 上下排布的垂直磁场绝对误差图

Fig. 13 Absolute error of vertical magnetic field in longitudinal arrangement

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 左右排布的垂直磁场绝对误差图

Fig. 14 Absolute error of vertical magnetic field in horizontal arrangement

仿真结果表明，在聚变装置CS线圈的电磁仿真研究中，通过结合无扭转CICC的详细结构，可以有效降低高温超导带材的垂直磁场计算误差，有助于更加精确地分析聚变装置超导磁体系统的临界电流性能。同时，较大的计算误差也表明，仅通过平均电流分布无法准确模拟CS线圈中沿高温超导带材垂直方向的磁场分布情况，需要探索新的仿真方法进行计算模拟。

5 结论

1）通过对线圈截面的平均电流密度分布假设，可以极大降低聚变高温超导磁体系统的电磁仿真模型的复杂度，进一步通过该建模方法可以对TF、CS、PF线圈上的磁场分布以及等离子体区域的中心磁场、波纹度分布情况进行仿真分析。

2）在计算模型的简化方面，当考虑等离子体区域的中心磁场和波纹度时，可以忽略CS与PF线圈的影响，只对TF线圈进行建模、仿真分析。当考虑CS线圈上的磁场分布时，可以忽略TF线圈的影响，将模型简化为二维轴对称模型。结合无扭转CICC详细结构的仿真结果表明，通过施加更加精细的电流分布，可以有效降低高温超导带材垂直磁场的仿真计算误差。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

万宝年，徐国盛．

EAST全超导托卡马克高约束稳态运行实验研究进展

[J]．中国科学(物理学力学天文学)，2019，49(4)：43-55． doi:10.1360/sspma2018-00233