虚拟电厂运行策略及DG分布式控制研究

doi:10.12096/j.2096-4528.pgt.23041

虚拟电厂运行策略及DG分布式控制研究

段贵超, 王恭, 曹生现, 段洁

东北电力大学自动化工程学院，吉林省吉林市 132012

Research on Operation Strategy of Virtual Power Plant and Distributed Control of DG

DUAN Guichao, WANG Gong, CAO Shengxian, DUAN Jie

School of Automatic Engineering, Northeast Electric Power University, Jilin 132012, Jilin Province, China

收稿日期: 2023-04-10 修回日期: 2023-09-12

基金资助:

吉林省科技发展计划项目. 20220203102SF. 20230203177SF

Received: 2023-04-10 Revised: 2023-09-12

作者简介 About authors

段贵超(1996)，男，硕士研究生，主要从事多智能体系统及微电网系统方面的研究，duanguichao@163.com；

王恭(1980)，男，博士，高级实验师，主要从事工业自动化及可再生能源利用方面的研究，本文通信作者，wg_neiep@163.com。

摘要

目的虚拟电厂通常由分布式发电(distributed generator，DG)单元组成，当系统缺少电网支撑时，需要合理的综合运行策略和准确的控制方法保证虚拟电厂平稳运行。方法首先，针对虚拟电网发电问题提出了一种基于功率差余值的运行策略。然后，针对系统中DG的发电控制问题设计了一种有限时间分布式控制器。将电压和频率的幅值在有限时间内调整到标称值，并实现了有功功率在各DG单元间的分配。与传统的集中式控制策略不同，所建立的控制方法基于分布式结构，只需要相邻DG单元之间通过稀疏通信网络进行信息交换。结果通过仿真实验验证了该控制方法的可行性，以及对模型参数不确定性和负载变化的鲁棒性。结论与以往研究相比，所提出的运行策略对系统工况进行了更为详细地划分，有效提高了系统的稳定性和安全性。

关键词： 虚拟电厂 ; 运行策略 ; 初级控制 ; 二级控制 ; 有限时间控制

Abstract

Objectives Virtual power plant is usually composed of distributed generator (DG). When the system lacks power grid support, practical and reasonable comprehensive operation strategies and accurate control methods are needed to ensure the smooth operation of virtual power plant. Methods An operation strategy based on system fluctuation value was proposed. Then, aiming at the problem of generation control of distributed generators in the system, a distributed finite-time controller was designed. The amplitudes of voltage and frequency were adjusted to nominal values within a finite time, and the active power was distributed among each DG unit. Different from the traditional centralized control strategy, the proposed control method is based on distributed junction, which only requires information exchange between adjacent DG units through sparse communication network. Results The feasibility of the proposed control method and its robustness to the uncertainty of model parameters and load variation were verified by simulation experiments. Conclusions Compared with previous studies, the proposed operation strategy divides the system operating conditions in more detail, effectively improving the stability and security of the system.

Keywords： virtual power plant ; operation strategy ; primary control ; secondary control ; finite-time control

PDF (1965KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

段贵超, 王恭, 曹生现, 段洁. 虚拟电厂运行策略及DG分布式控制研究. 发电技术[J], 2024, 45(4): 765-771 DOI:10.12096/j.2096-4528.pgt.23041

DUAN Guichao, WANG Gong, CAO Shengxian, DUAN Jie. Research on Operation Strategy of Virtual Power Plant and Distributed Control of DG. Power Generation Technology[J], 2024, 45(4): 765-771 DOI:10.12096/j.2096-4528.pgt.23041

0 引言

近年来，包含多种分布式电源的虚拟电厂和微电网系统得到了广泛研究^[1-5]。以包含风电和光伏的发电系统为例，世界上许多国家已经建立了相关的实用系统^[6-7]。

一个虚拟电厂系统可分为物理层和控制层。物理层包含系统必要的基础设施，可由光伏、风力涡轮机、分布式发电(distributed generator，DG)单元以及负载组成。控制层内置针对各发电单元的运行策略及控制算法^[8]，如风力发电机和光伏发电设备通常采用最大功率点跟踪控制方法。然而，由于风电和光伏发电的输出具有波动性及间歇性，随着天气条件的变化，系统功率的缺额必须由火电等调峰电源补充。因此，针对DG的控制方法进行研究十分必要。

目前针对DG单元所采用的初级控制常常会导致频率和电压偏差，因此需要采用二级控制来进一步调节^[9-10]。集中式控制方法是二级控制的传统方法，它避免了偏差，但其复杂的信息传输网络结构降低了集中式控制器的可靠性，提高了故障灵敏度^[11-12]。

为了避免上述问题，分布式协同控制策略成为另一种选择。文献[13-14]首次提出了基于分布式协同控制策略的二次控制方法。文献[15]提出了一种基于一致性的两级分布式控制框架。文献[16]实现了加权一致的减载协议，以保持孤岛系统的稳定。文献[17]提出了一种在有限时间内实现频率和电压恢复的二次控制方法。

本文针对虚拟电厂的运行及系统中DG单元控制问题开展研究。首先针对虚拟电网发电问题提出了一种基于功率差余值的运行策略，保证虚拟电网在不同工况下的安全运行。然后针对系统中DG的发电控制问题设计了一种分布式有限时间二级控制方案，在有限时间内消除初级控制偏差，保证频率和电压恢复到标称值并实现了有功功率在各DG单元间的分配。最后，通过仿真实验，验证本文所提控制方法的可行性及其对模型参数不确定性和负载变化的鲁棒性。

1 虚拟电厂运行策略

虚拟电厂中的风力发电机组和光伏发电系统受到天气因素的影响，其出力存在间歇性和随机性等特点，将导致系统功率频繁波动。同时，负载端的需求变化会使得系统中各单元的工作状态频繁改变，严重影响系统的稳定性和安全性。因此，为系统制定合理的运行策略以提高系统的动态稳定性十分必要。

考虑到系统中各供能单元的不同动态调节特性，本研究根据风力发电功率P_wind、光伏发电功率P_pv与负载调度需求功率P_l得到系统功率差余值 $N_{c}$ ：

N_{c} = P_{l} - P_{w i n d} - P_{p v}

(1)

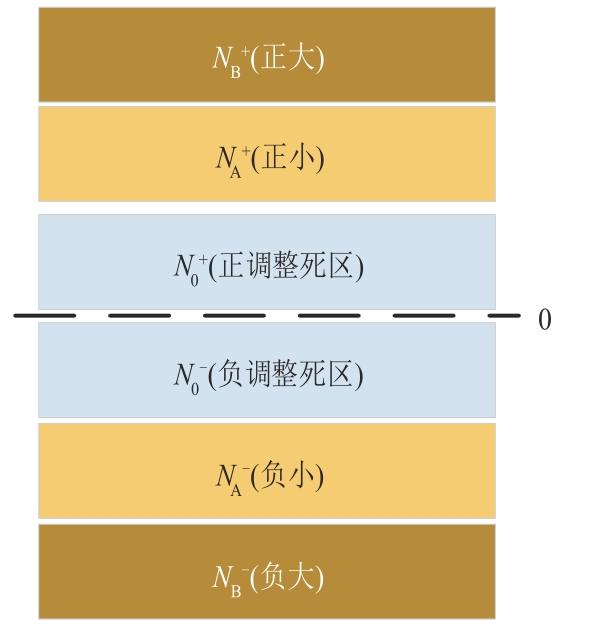
根据图1所示的方法，将系统功率差余值分为6个阈值区间以表示系统不同程度的功率波动情况，分别为N_B⁺(正大)、N_A⁺(正小)、N₀⁺(正调整死区)、N₀^-(负调整死区)、N_A^-(负小)、N_B^-(负大)。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 差余值N_c的区间划分

Fig. 1 Interval partition of N_c

当差余值满足N₀^-≤N_c≤N₀⁺时，表明系统供需失衡程度非常小，系统通过自身惯性即可保证稳定，不需要分布式发电机承担调节波动。

当差余值满足 ${N_{0}}^{+} \leq N_{c} \leq {N_{A}}^{+}$ 时，表明系统供需失衡的程度较高，通过分布式发电机组高功率稳定输出，补充系统功率缺额。

当差余值满足 ${N_{A}}^{+} \leq N_{c} \leq {N_{B}}^{+}$ 时，表明系统出现极端电力缺额。通常情况是负载端出现异常，此时需强制切断运行开关以保证系统各硬件设施安全。

当差余值满足 ${N_{A}}^{-} \leq N_{c} \leq {N_{0}}^{-}$ 时，表明系统中的风电与光电超出负载所需，此时通常采用外接储能单元或并入大电网等方式储存或消耗多余电能。

当差余值满足 ${N_{B}}^{-} \leq N_{c} \leq {N_{A}}^{-}$ 时，表明系统遇到强烈极端天气，此时如果继续运行系统，将会导致系统各零部件受损，因此应切断系统，保证系统中各硬件设施安全。

2 DG单元控制

2.1 初级控制

下垂控制方法作为一种常用的初级控制策略，可以实现各DG单元自主控制。因此，本研究采用下垂控制方法对基于逆变器的可控DG机组进行局部一次控制，在负载变化时局部调整频率和电压幅值，同时根据下垂系数保证DG之间适当的功率共享。

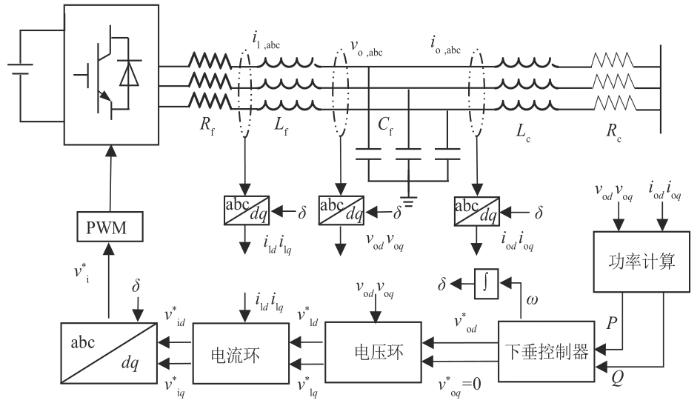
本研究中初级控制的基本原理如图2所示，由功率控制器和电压电流控制器^[6]组成。图中 $δ$ 表示相位角； $i_{l d}$ 、 $i_{l q}$ ， $v_{o d}$ 、 $v_{o q}$ ， $i_{o d}$ 、 $i_{o q}$ 分别为电感电流 $i_{l, a b c}$ 、测量输出电压 $v_{o, a b c}$ 和输出电流 $i_{o, a b c}$ 的分解项。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 初级控制结构

Fig. 2 Structure of primary control

下垂控制器可以表示为

\{\begin{array}{l} ω_{i} = ω_{n i} - m P_{i} \\ v_{o d i}^{*} = V_{n i} - n Q_{i} \\ v_{o q i}^{*} = 0 \end{array}

(2)

式中： $m$ 和 $n_{}$ 分别为频率和电压的下垂系数，通常根据每个逆变器的输出额定功率来确定； $ω_{n i}$ 和 $V_{n i}$ 分别为一次控制的频率和电压幅值设定值； $P_{i}$ 和 $Q_{i}$ 分别为低通滤波器测量的有功功率和无功功率。计算得到的 $ω_{i}$ 和 $v_{o d i}^{*}$ 分别作为参考值送至内部电压/电流控制环。考虑到DG单元的电压可表示为 $V_{i} = \sqrt[]{{v_{o d i}^{*}}^{2} + {v_{o q i}^{*}}^{2}}$ 。因此， $V_{i}$ 可用来代替 $v_{o d i}^{*}$ 。

2.2 二级控制

由于下垂控制存在控制偏差，需要二级控制消除初级控制带来的频率及电压偏差。考虑到DG单元的分布式特点，本文将二级控制问题转化为多智能体同步跟踪问题，利用各DG单元间的信息交互，采用分布式算法实现二次控制^[7]。

2.2.1 图论

DG网络的通信拓扑可以用包含领导者的无向图 $\bar{𝒢} = 𝒢$ ∪ ${0}$ 来表示，其中 $0$ 表示领导者。 $𝒢 = (𝒱, ε, 𝒜)$ 可用于描述追随者之间的信息传递。 $𝒱 = {1,2, \dots, N}$ 是N个agent的非空有限集，每个agent代表一个DG。 $ε \subset 𝒱 \times 𝒱$ 表示边集合，每条边都表示通信链路。( $i, j$ )用于表示从节点 $i$ 开始并结束于节点 $j$ 的边，节点 $j$ 被称为节点 $i$ 的邻居。 $𝒜 = [a_{i j}] \in R^{n \times n}$ 是由图 $𝒢$ 的边权值所构成的关联邻接矩阵，假定边权值都满足非负， $a_{i j}$ 是边( $i, j$ )的权值，若 $(i, j) \in ε$ ，则 $a_{i j} = a_{j i} > 0$ 。入度矩阵为 $D = d i a g {d_{i}} \in R^{N \times N}$ ， $d_{i} = \sum_{j = 1}^{N} a_{i j}$ 。 $𝒢$ 的拉普拉斯矩阵定义为 $L = D - 𝒜$ 。定义邻接矩阵 $B = d i a g {b_{1}, \dots, b_{N}} \in R^{N \times N}$ 来表示领导者和追随者之间的关系，如果节点 $i$ 能够观察领导者，则 $b_{i} > 0$ ，否则 $b_{i} = 0$ 。最后，定义一个矩阵 $H = L + B$ 。

2.2.2 二级控制器设计

为了实现二级控制器设计，首先介绍如下假设和引理。

假设1：至少有一个追随者可以访问领导者所提供的信息，且无向图 $𝒢$ 是连通的。

引理1：如果假设1成立，则 $H$ 是正定的。

引理2^[18]：考虑如下系统

\dot{z} (t) = f (z (t)), z (0) = z_{0}

(3)

式中： $z \in R^{n}$ ； $f (\cdot)$ 为连续函数，满足 $f (0) = 0$ 。考虑连续正定函数 $V (z) : R^{n} \to R_{0}^{+}$ ，常数 $a > 0$ ， $c > 0$ 和 $β \in (0,1)$ 使得

\dot{V} (z) + a [V (z)] + c [V {(z)]}^{β} \leq 0, z \in R^{n} \ {0}

(4)

成立，则称系统原点是快速有限时间稳定的，稳定时间可以表示为

T \leq \frac{1}{a (1 - β)} l n {\frac{a V [z {(0)]}^{1 - β} + c}{c}}

(5)

为了恢复频率并保证功率共享，对下垂方程求导，以频率变化率和有功功率为控制变量，设置辅助控制输入 $K^{ℏ}$ 和 $K^{ƛ}$ ，如下所示：

{\dot{ω}}_{n i} = K^{ℏ} + K^{^{ƛ}}, i = 1,2, 3, \dots, N

(6)

辅助控制被设计为如下的分布式有限时间协议：

K^{ℏ} = - χ ε_{i} - ς s i g {ε_{i}}^{α}

(7)

K^{ƛ} = 𝓁 \sum_{j = 1}^{N} a_{i j} s i g (ϖ_{j} - ϖ_{i})^{α} =

𝓁 \sum_{j = 1}^{N} a_{i j} s i g (ϖ_{j} - ϖ_{i}) {|ϖ_{j} - ϖ_{i}|}^{α}

(8)

式中： $ε_{i} = \sum_{j = 1}^{N} a_{i j} (ω_{i} - ω_{j}) + b_{i} (ω_{i} - ω_{r e f})$ ； $χ > 0$ ； $ς > 0$ ； $α \in (0,1)$ ； $ϖ_{i} = m_{i} P_{i}$ ； $i \in {1,2, \dots, N}$ ； $𝓁$ 表示正控制增益。

定理1：假设1成立，则控制算法(7)和(8)可以实现频率 $ω_{^{r e f}}^{}$ 快速收敛到额定频率，并在有限时间内保持功率共享。

证明：定义错误变量 ${\bar{ω}}_{i} = ω_{i} - ω_{r e f}$ ，可以得到

{\dot{\bar{ω}}}_{i} = - χ ε_{i} - ς s i g {ε_{i}}^{α}

(9)

令 $\bar{ω} = ({\bar{ω}}_{1}, {\bar{ω}}_{2}, \dots, {\bar{ω}}_{N})^{T}$ ，则式(9)的增广系统可表示为

\dot{\bar{ω}} = - χ H \bar{ω} - ς s i g {H \bar{ω}}^{α}

(10)

根据引理1，可以得知 $H$ 是对称正定的。

假设存在一个正交矩阵 $U \in R^{n \times n}$ ，满足 $U H U^{T} = J = d i a g (λ_{1}, λ_{2}, \dots, λ_{N}$ )。

考虑如下李亚普诺夫函数：

V_{ω} = {\bar{ω}}^{T} H \bar{ω}

(11)

令 $\tilde{ω} = U \bar{ω}$ ， $ξ = H \bar{ω}$ ，可得

{\dot{V}}_{ω} = - 2 χ {\bar{ω}}^{T} H^{2} \bar{ω} - 2 ς {\bar{ω}}^{T} H s i g {\{H \bar{ω}\}}^{α} =

- 2 χ {\tilde{ω}}^{T} J^{2} \tilde{ω} - 2 ς ξ^{T} s i g {ξ}^{α} =

- 2 χ \sum_{i = 1}^{N} {λ_{i}}^{2} {ω_{i}}^{2} - 2 ς ξ^{T} s i g {ξ}^{α}

(12)

可以得到

- 2 χ \sum_{i = 1}^{N} {λ_{i}}^{2} {ω_{i}}^{2} \leq - 2 χ {λ^{2}}_{m i n} H \sum_{i = 1}^{N} {ω_{i}}^{2} \leq

\frac{- 2 χ {λ^{2}}_{m i n} H}{λ_{m a x} H} V_{ω}

(13)

- 2 ς ξ^{T} s i g {ξ}^{α} \leq - 2 ς (λ_{m i n} H^{2} {\bar{ω}}^{T} {\bar{ω})}^{\frac{1 + α}{2}} \leq

- 2 ς {(\frac{λ_{m i n} H^{2}}{λ_{m a x} H})}^{\frac{1 + α}{2}} {V_{ω}}^{\frac{1 + α}{2}}

(14)

结合式(13)、(14)，可得

{\dot{V}}_{ω} \leq - \frac{2 χ {λ^{2}}_{m i n} H}{λ_{m a x} H} V_{ω} -

2 ς {(\frac{λ_{m i n} H^{2}}{λ_{m a x} H})}^{\frac{1 + α}{2}} {V_{ω}}^{\frac{1 + α}{2}}

(15)

根据引理2，可知 $\bar{ω} = 0$ 是快速有限时间稳定的，证明完成。辅助控制 $K^{ƛ}$ 的证明方法与上述方法类似。

为消除初级控制引起的电压偏差，对下垂方程求导，以电压变化率为控制变量，设置如下辅助控制 $K^{v}$ ：

K^{v} = - ι ξ_{i} - γ s i g {ξ_{i}}^{α}

(16)

式中： $ξ_{i} = \sum_{j = 1}^{N} a_{i j} (V_{i} - V_{j}) + b_{i} (V_{i} - V_{r e f})$ ； $ι > 0$ ； $γ > 0$ ； $α \in (0,1)$ 。

定理2：假设1成立，则控制算法(16)能在有限时间内实现电压快速收敛到额定电压 $V_{r e f}$ ，且时间满足

T \leq T^{*} ≜ \frac{λ_{m a x} H}{2 (1 - α) ι λ^{2} m i n (H)} \cdot

l n [\frac{ι λ^{2} m i n H}{γ λ_{m a x} H} {(\frac{λ_{m i n} H^{2}}{λ_{m a x} H})}^{\frac{1 + α}{2}} V_{v} {(0)}^{1 - α} + 1]

(17)

证明：定义误差变量 ${\bar{V}}_{i} = V_{i} - V_{r e f}$ 。

令 $\bar{V} = ({\bar{V}}_{1}, {\bar{V}}_{2}, \dots, {\bar{V}}_{N})^{T}$ ，可以得到增广系统

\dot{\bar{V}} = - ι H \bar{V} - γ s i g {H \bar{V}}^{α}

(18)

考虑如下的李雅普诺夫函数：

V_{v} = {\bar{V}}^{T} H \bar{V}

(19)

令 $\tilde{V} = U \bar{V}$ ， $ζ = H \bar{V}$ ，可得

${\dot{V}}_{v} = - 2 ι {\bar{V}}^{T} H^{2} \bar{V} - 2 γ {\bar{V}}^{T} H s i g {H \bar{V}}^{α}$ =

- 2 ι {\tilde{V}}^{T} J^{2} \tilde{V} - 2 γ ζ^{T} s i g {ζ}^{α} =

- 2 ι \sum_{i = 1}^{N} {λ_{i}}^{2} {V_{i}}^{2} - 2 γ ζ^{T} s i g {ζ}^{α}

(20)

与定理1的证明相似，不难得到

{\dot{V}}_{v} \leq - \frac{2 ι {λ^{2}}_{m i n} H}{λ_{m a x} H} V_{v} - 2 γ {(\frac{λ_{m i n} H^{2}}{λ_{m a x} H})}^{\frac{1 + α}{2}} {V_{v}}^{\frac{1 + α}{2}}

(21)

根据引理2， $\bar{V} = 0$ 是快速有限时间稳定的，且收敛时间满足式(17)，证明完成。

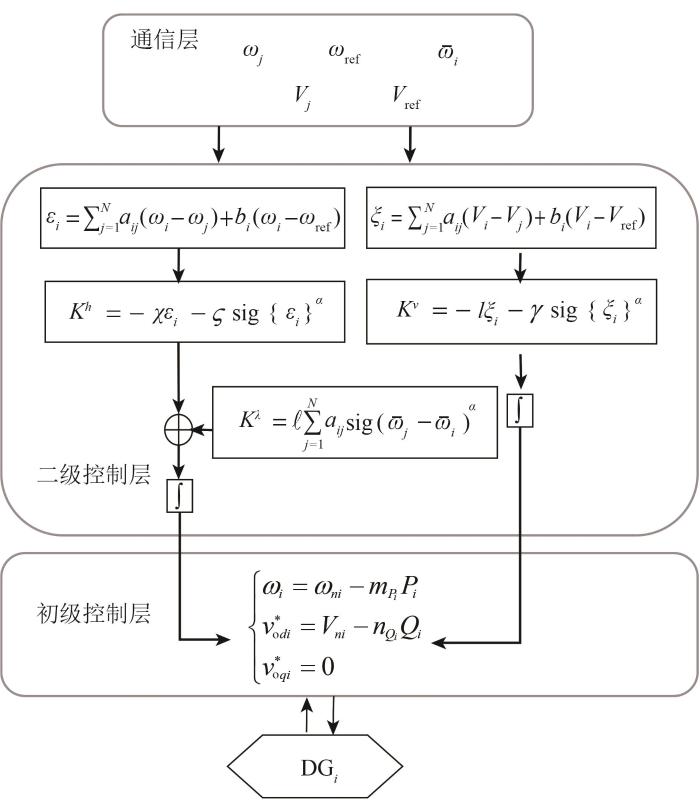
综上所述，分布式二级控制方案如图3所示。DG _i 通过稀疏通信网络从相邻的DG _j 采集频率、电压和有功功率的测量值，通过本研究提出的二级控制策略实现频率、电压的无差调节，并保证各DG单元的有功功率分配。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 二级控制结构

Fig. 3 Structure of secondary control

3 仿真实验

为验证本文所提出的分布式二级控制方法的可行性，并探究其在负荷变化和模型参数不确定情况下的鲁棒性能，本研究搭建了一个包含4个DG单元并联的仿真系统，标准电压设置为380 V，频率为50 Hz，仿真系统中的主要参数如表1所示。

表1 系统参数

Tab. 1 Parameters of the system

参数	数值
参数	DG₁	DG₂	DG₃	DG₄
m	1×10^-5	14×10^-5	1.8×10^-5	2.5×10^-5
n R_f/Ω L_f/mH C_f/F KPV KIV KPC	5×10^-4 1×10^-3 1.4 6×10^-5 0.1 120 7	8×10^-4 1×10^-3 1.4 6×10^-5 0.1 120 7	8×10^-4 1×10^-3 1.4 6×10^-5 0.1 120 7	9×10^-4 1×10^-3 1.4 6×10^-5 0.1 120 7
KIC	20 000	20 000	20 000	20 000

新窗口打开| 下载CSV

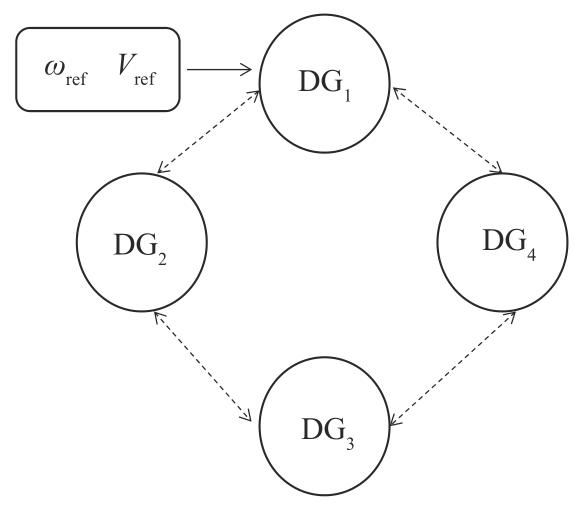
DG单元的通信拓扑结构如图4所示，4个DG单元可两两进行通信，并由DG₁接收虚拟领导者所提供的标准频率和标准电压信息。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 DG单元的通信拓扑结构

Fig. 4 Communication topology of DG

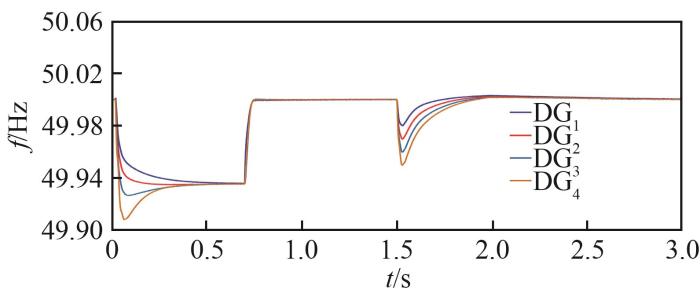
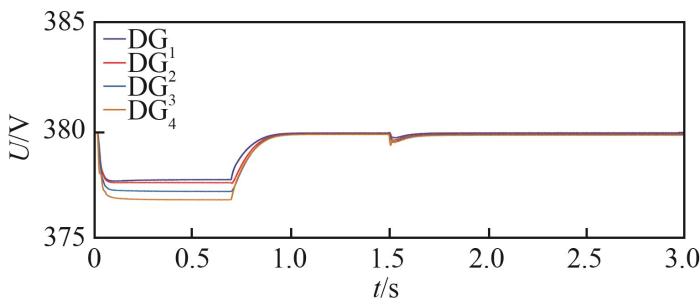
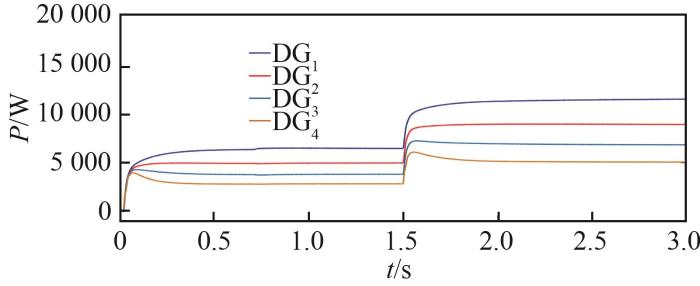
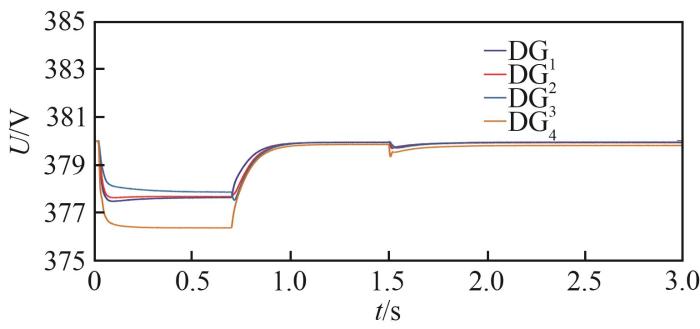
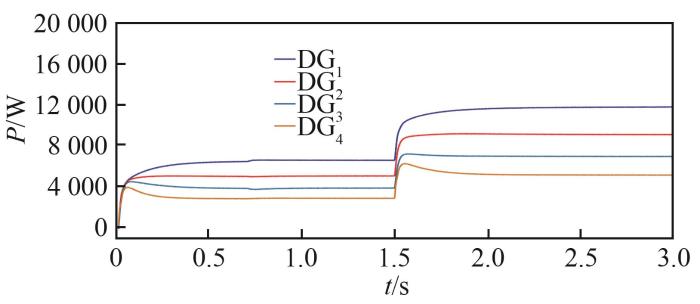
最初，各DG单元仅由初级控制器控制，系统中连接一个20 kW的负载。在t=1 s时采用本研究的分布式二级控制策略。t=1.5 s时负载端增加15 kW负荷。仿真结果如图5—7所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 频率仿真结果

Fig. 5 Simulation results of frequency

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 电压仿真结果

Fig. 6 Simulation results of voltage

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 有功功率仿真结果

Fig. 7 Simulation results of active power

由上述仿真结果可以看出，在仅使用初级控制时，各DG单元的频率和电压会发生偏差。加入分布式二级控制后，频率和电压在很短的时间恢复到额定值。此外，即使负荷发生变化，DG单元的频率和电压也可迅速恢复到预期值并保持有功功率分配，说明该控制方案仍然有效。需要强调的是，由于线路阻抗的存在，系统必然存在一定的消耗。

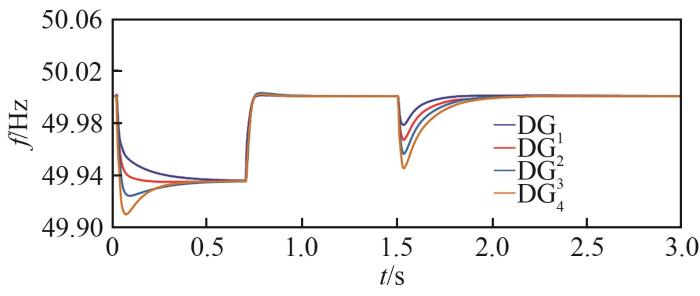
为了进一步检验该方法针对参数扰动下的鲁棒性，在各参数条件保持不变的情况下，将线阻抗调整为10%~30%的随机波动。仿真结果如图8—10所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 扰动下的频率

Fig. 8 Frequency under disturbance

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 扰动下的电压

Fig. 9 Voltage under disturbance

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 扰动下的有功功率

Fig. 10 Active power under disturbance

从仿真结果可以看出，即使存在参数扰动，所提控制方法也能将电压和频率迅速恢复到期望值，并实现有功功率分配，说明所提控制方法对系统扰动具有良好鲁棒性。

4 结论

针对虚拟电厂的运行及系统中DG单元控制问题开展研究，主要结论如下：

1）针对虚拟电厂发电问题，提出了一种基于新能源功率与需求平衡的运行策略。该策略充分考虑到虚拟电厂中各供能单元的不同动态调节特性，根据风力发电功率、光伏发电功率与负载调度需求功率得到系统功率差余值，基于差余值设计了不同工况下的系统运行策略。与以往研究相比，提出的运行策略对系统工况进行了更为详细的划分，有效提高了系统的稳定性和安全性。

2）针对系统中的DG单元，提出了一种分布式有限时间二级控制方案，在有限时间内迅速恢复初级控制所引起的频率和电压偏差，并实现了有功功率共享。与以往的研究相比，所提出的方法仅需要稀疏通信网络，并可在有限时间内恢复频率和电压幅值，具有更好的控制性能。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

宣文博，李慧，刘忠义，等．

一种基于虚拟电厂技术的城市可再生能源消纳能力提升方法

[J]．发电技术，2021，42(3)：289-297． doi:10.12096/j.2096-4528.pgt.20104

[本文引用: 1]

XUAN

W B

， LI

， LIU

Z Y

，et al ．

A method for improving the accommodating capability of urban renewable energy based on virtual power plant technology

[J]．Power Generation Technology，2021，42(3)：289-297． doi:10.12096/j.2096-4528.pgt.20104

[本文引用: 1]

[2]

赵建立，向佳霓，汤卓凡，等．

虚拟电厂在上海的实践探索与前景分析

[J]．中国电力，2023，56(2)：1-13． doi:10.11930/j.issn.1004-9649.202208078

ZHAO

J L

， XIANG

J N

， TANG

Z F

，et al ．

Practice exploration and prospect analysis of virtual power plant in Shanghai

[J]．Electric Power，2023，56(2)：1-13． doi:10.11930/j.issn.1004-9649.202208078

[3]

张天翼，郑凯元，王海风．

聚合相同分布式电源对直流微电网高频振荡稳定性的影响

[J]．中国电力，2021，54(8)：103-108．

ZHANG

T Y

， ZHENG

K Y

， WANG

H F

．

Impact of large number of same aggregated distributed generators on the high-frequency oscillatory stability of a DC microgrids

[J]．Electric Power，2021，54(8)：103-108．

[4]

霍龙，张誉宝，陈欣．

人工智能在分布式储能技术中的应用

[J]．发电技术，2022，43(5)：707-717． doi:10.12096/j.2096-4528.pgt.22109

HUO

， ZHANG

Y B

， CHEN

．

Artificial intelligence applications in distributed energy storage technologies

[J]．Power Generation Technology，2022，43(5)：707-717． doi:10.12096/j.2096-4528.pgt.22109

[5]

李靖，王志和，倪浩．

基于改进下垂控制的直流微网运行研究

[J]．发电技术，2021，42(6)：765-774． doi:10.12096/j.2096-4528.pgt.21003

[本文引用: 1]

， WANG

Z H

， NI

．

Research on DC microgrid operation based on improved droop control

[J]．Power Generation Technology，2021，42(6)：765-774． doi:10.12096/j.2096-4528.pgt.21003

[本文引用: 1]

[6]

王睿，孙秋野，张化光．

微电网的电流均衡/电压恢复自适应动态规划策略研究

[J]．自动化学报，2022，48(2)：479-491．

[本文引用: 2]

WANG

， SUN

Q Y

， ZHANG

H G

．

Research on current sharing/voltage recovery based adaptive dynamic programming control strategy of microgrids

[J]．Acta Automatica Sinica，2022，48(2)：479-491．

[本文引用: 2]

[7]

MEHRJERDI

， HEMMATI

， SHAFIE-KHAH

，et al ．

Zero energy building by multicarrier energy systems including hydro，wind， solar， and hydrogen

[J]．IEEE Transactions on Industrial Informatics， 2021，17(8)：5474-5484． doi:10.1109/tii.2020.3034346

[本文引用: 2]

[8]

杨继鑫，王久和，王勉，等．

基于无源控制的光储直流微网虚拟惯性控制策略研究

[J]．发电技术，2021，42(5)：576-584． doi:10.12096/j.2096-4528.pgt.20080

[本文引用: 1]

YANG

J X

， WANG

J H

， WANG

，et al ．

Research on virtual inertial control strategy of DC microgrid with photovoltaic and storage system based on passivity-based control

[J]．Power Generation Technology，2021，42(5)：576-584． doi:10.12096/j.2096-4528.pgt.20080

[本文引用: 1]

[9]

NIMA

M D

， NASSER

， MOHSEN

．

Fully distributed cooperative secondary frequency and voltage control of islanded microgrids

[J]．IEEE Transactions on Energy Conversion，2017，32(2)：675-685． doi:10.1109/tec.2016.2638858

[本文引用: 1]

[10]

MICHELE

， GIAN

P I

， ANTONELLA

．

Decentralized sliding mode control of islanded AC microgrids with arbitrary topology

[J]．IEEE Transactions on Industrial Electronics，2017，64(8)：6706-6713． doi:10.1109/tie.2017.2694346

[本文引用: 1]

[11]

XIA

S W

， BU

S Q

， WAN

，et al ．

A fully distributed hierarchical control framework for coordinated operation of DERs in active distribution power networks

[J]．IEEE Transactions on Power Systems，2019，34(6)：5184-5197． doi:10.1109/tpwrs.2018.2870153

[本文引用: 1]

[12]

J Y

， BHOWMICK

．

A consensus-based robust secondary voltage and frequency control scheme for islanded microgrids

[J]．IEEE Transactions on Power Systems，2020，116：105575． doi:10.1016/j.ijepes.2019.105575

[本文引用: 1]

[13]

BIDRAM

， DAVOUDI

， FRANK

，et al ．

Secondary control of microgrids based on distributed cooperative control of multi-agent systems

[J]．IET Generation Transmission & Distribution，2013，7(8)：822-831． doi:10.1049/iet-gtd.2012.0576

[本文引用: 1]

[14]

BIDRAM

， DAVOUDI

， FRANK

，et al ．

Cooperative secondary control of microgrids using feedback linearization

[J]．IEEE Transactions on Power Systems，2013，28(3)：3462-3470． doi:10.1109/tpwrs.2013.2247071

[本文引用: 1]

[15]

ZHOU

， TIAN

， MOHAMMAD

，et al ．

Optimal consensus-based distributed control strategy for coordinated operation of networked microgrids

[J]．IEEE Transactions on Power Systems，2020，35(3)：2452-2462． doi:10.1109/tpwrs.2019.2954582

[本文引用: 1]

[16]

XIE

， LIU

C C

， MARINO

，et al ．

Consensus weighting of a multi-agent system for load shedding

[J]．International Journal of Electrical Power & Energy Systems，2020，117：105615． doi:10.1016/j.ijepes.2019.105615

[本文引用: 1]

[17]

Y L

， SUN

H B

， GU

，et al ．

Optimal distributed control for secondary frequency and voltage regulation in an islanded microgrid

[J]．IEEE Transactions on Industrial Informatics，2019，15(1)：225-235． doi:10.1109/tii.2018.2795584

[本文引用: 1]

[18]

KHOO

S Y

， XIE

L H

， ZHAO

S K

，et al ．

Multi-surface sliding control for fast finite-time leader-follower consensus with high order SISO uncertain nonlinear agents

[J]．International Journal of Robust and Nonlinear Control，2014，24(16)：2388-2404． doi:10.1002/rnc.2997

[本文引用: 1]

一种基于虚拟电厂技术的城市可再生能源消纳能力提升方法

2021

... 近年来，包含多种分布式电源的虚拟电厂和微电网系统得到了广泛研究^[1-5].以包含风电和光伏的发电系统为例，世界上许多国家已经建立了相关的实用系统^[6-7]. ...

A method for improving the accommodating capability of urban renewable energy based on virtual power plant technology

2021

虚拟电厂在上海的实践探索与前景分析

2023

Practice exploration and prospect analysis of virtual power plant in Shanghai

2023

聚合相同分布式电源对直流微电网高频振荡稳定性的影响

2021

Impact of large number of same aggregated distributed generators on the high-frequency oscillatory stability of a DC microgrids

2021

人工智能在分布式储能技术中的应用

2022

Artificial intelligence applications in distributed energy storage technologies

2022

基于改进下垂控制的直流微网运行研究

2021

Research on DC microgrid operation based on improved droop control

2021

微电网的电流均衡/电压恢复自适应动态规划策略研究

2022

... 本研究中初级控制的基本原理如图2所示，由功率控制器和电压电流控制器^[6]组成.图中

δ

表示相位角；

i_{l d}

、

i_{l q}

，

v_{o d}

、

v_{o q}

，

i_{o d}

、

i_{o q}

分别为电感电流

i_{l, a b c}

、测量输出电压

v_{o, a b c}

和输出电流

i_{o, a b c}

的分解项. ...

Research on current sharing/voltage recovery based adaptive dynamic programming control strategy of microgrids

2022

... 本研究中初级控制的基本原理如图2所示，由功率控制器和电压电流控制器^[6]组成.图中

δ

表示相位角；

i_{l d}

、

i_{l q}

，

v_{o d}

、

v_{o q}

，

i_{o d}

、

i_{o q}

分别为电感电流

i_{l, a b c}

、测量输出电压

v_{o, a b c}

和输出电流

i_{o, a b c}

的分解项. ...

Zero energy building by multicarrier energy systems including hydro，wind， solar， and hydrogen

2021

... 由于下垂控制存在控制偏差，需要二级控制消除初级控制带来的频率及电压偏差.考虑到DG单元的分布式特点，本文将二级控制问题转化为多智能体同步跟踪问题，利用各DG单元间的信息交互，采用分布式算法实现二次控制^[7]. ...

基于无源控制的光储直流微网虚拟惯性控制策略研究

2021

... 一个虚拟电厂系统可分为物理层和控制层.物理层包含系统必要的基础设施，可由光伏、风力涡轮机、分布式发电(distributed generator，DG)单元以及负载组成.控制层内置针对各发电单元的运行策略及控制算法^[8]，如风力发电机和光伏发电设备通常采用最大功率点跟踪控制方法.然而，由于风电和光伏发电的输出具有波动性及间歇性，随着天气条件的变化，系统功率的缺额必须由火电等调峰电源补充.因此，针对DG的控制方法进行研究十分必要. ...

Research on virtual inertial control strategy of DC microgrid with photovoltaic and storage system based on passivity-based control

2021

Fully distributed cooperative secondary frequency and voltage control of islanded microgrids

2017

... 目前针对DG单元所采用的初级控制常常会导致频率和电压偏差，因此需要采用二级控制来进一步调节^[9-10].集中式控制方法是二级控制的传统方法，它避免了偏差，但其复杂的信息传输网络结构降低了集中式控制器的可靠性，提高了故障灵敏度^[11-12]. ...

Decentralized sliding mode control of islanded AC microgrids with arbitrary topology

2017

A fully distributed hierarchical control framework for coordinated operation of DERs in active distribution power networks

2019

A consensus-based robust secondary voltage and frequency control scheme for islanded microgrids

2020

Secondary control of microgrids based on distributed cooperative control of multi-agent systems

2013

... 为了避免上述问题，分布式协同控制策略成为另一种选择.文献[13-14]首次提出了基于分布式协同控制策略的二次控制方法.文献[15]提出了一种基于一致性的两级分布式控制框架.文献[16]实现了加权一致的减载协议，以保持孤岛系统的稳定.文献[17]提出了一种在有限时间内实现频率和电压恢复的二次控制方法. ...

Cooperative secondary control of microgrids using feedback linearization

2013

Optimal consensus-based distributed control strategy for coordinated operation of networked microgrids

2020

Consensus weighting of a multi-agent system for load shedding

2020

Optimal distributed control for secondary frequency and voltage regulation in an islanded microgrid

2019

Multi-surface sliding control for fast finite-time leader-follower consensus with high order SISO uncertain nonlinear agents

2014

... 引理2^[18]：考虑如下系统 ...

〈

〉