一种新型分布式光伏出力区间预测方法

doi:10.12096/j.2096-4528.pgt.23045

一种新型分布式光伏出力区间预测方法

杨康¹, 李蓝青¹, 李艺丰¹, 宋东阔², 王博仑¹, 陈金², 周霞³, 单宇³

1.国网江苏省电力有限公司，江苏省南京市 210008

2.国电南瑞科技股份有限公司，江苏省南京市 211000

3.南京邮电大学自动化学院/人工智能学院，江苏省南京市 210023

A Novel Distributed Photovoltaic Output Interval Prediction Method

YANG Kang¹, LI Lanqing¹, LI Yifeng¹, SONG Dongkuo², WANG Bolun¹, CHEN Jin², ZHOU Xia³, SHAN Yu³

1.State Grid Jiangsu Electric Power Co. , Ltd. , Nanjing 210008, Jiangsu Province, China

2.Guodian NARI Technology Co. , Ltd. , Nanjing 211000, Jiangsu Province, China

3.College of Automation/College of Artificial Intelligence, Nanjing University of Posts and Telecommunications, Nanjing 210023, Jiangsu Province, China

收稿日期: 2023-04-12 修回日期: 2023-08-25

基金资助:

国家自然科学基金项目. 61933005

Received: 2023-04-12 Revised: 2023-08-25

作者简介 About authors

杨康(1990)，男，硕士，工程师，主要研究方向为电力电子，yangkangtc@163.com；

周霞(1978)，女，博士，副教授，从事电力通信、电力系统分析与控制研究，本文通信作者，zhouxia@njupt.edu.cn。

摘要

目的分布式光伏功率预测对光伏电站运行和调度具有重要意义，针对点预测方法难以全面描绘分布式光伏功率不确定性的问题，提出了一种基于自适应噪声完备集合经验模态分解(complete ensemble empirical mode decomposition with adaptive noise，CEEMDAN)和麻雀搜索算法优化的最小二乘支持向量机(sparrow search algorithm optimized least square support vector machine，SSA-LSSVM)分布式光伏功率区间预测模型。方法首先，通过CEEMDAN将光伏功率序列分解为多个模态分量，再对一次分解得到的高频非平稳分量进行二次分解；其次，采用样本熵(sample entropy，SE)将所有分量重构为趋势分量和振荡分量；然后，通过SSA-LSSVM得到2个分量的点预测值；最后，对振荡分量的点预测误差进行概率密度估计，叠加点预测值得到总体的预测区间结果。结果所提区间预测模型具有更高的区间覆盖率且区间平均宽度更窄。结论在分布式光伏功率数据处理中加入二次模态分解，再结合样本熵对其子序列进行重构，可有效降低原始预测分量的复杂程度，同时提升模型预测准确性。

关键词： 分布式光伏 ; 功率预测 ; 核密度估计 ; 区间预测

Abstract

Objectives Distributed photovoltaic power prediction is of great significance for the operation and scheduling of photovoltaic power plants. Point prediction methods are difficult to comprehensively describe the uncertainty of distributed photovoltaic power. This article proposed a distributed photovoltaic power interval prediction model based on complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) and sparrow search algorithm optimized least squares support vector machine (SSA-LSSVM). Methods Firstly, the photovoltaic sequence was broken down into multimodal components through CEEMDAN, and then the high-frequency non-stationary components obtained from the first decomposition were decomposed twice. Secondly, sample entropy (SE) was used to reconstruct all components into trend and oscillation components. Then, the point prediction values of the two components were obtained through SSA-LSSVM. Finally, the probability density estimation was performed on the point prediction error of the oscillation component, and the stacked point prediction value was used to obtain the overall prediction interval result. Results The interval prediction model proposed in this paper has higher interval coverage and narrower average interval width. Conclusions Adding secondary modal decomposition to distributed photovoltaic power data processing and combining sample entropy to reconstruct its sub-sequences can effectively reduce the complexity of the original prediction components and improve the accuracy of model prediction.

Keywords： distributed photovoltaic ; power prediction ; kernel density estimation ; intervel prediction

PDF (3317KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

杨康, 李蓝青, 李艺丰, 宋东阔, 王博仑, 陈金, 周霞, 单宇. 一种新型分布式光伏出力区间预测方法. 发电技术[J], 2024, 45(4): 684-695 DOI:10.12096/j.2096-4528.pgt.23045

YANG Kang, LI Lanqing, LI Yifeng, SONG Dongkuo, WANG Bolun, CHEN Jin, ZHOU Xia, SHAN Yu. A Novel Distributed Photovoltaic Output Interval Prediction Method. Power Generation Technology[J], 2024, 45(4): 684-695 DOI:10.12096/j.2096-4528.pgt.23045

0 引言

分布式光伏发电的出力预测是光伏电站运行和调度的重要组成部分^[1-6]，对于提高光伏电站的发电量、降低发电成本具有重要意义。然而，分布式光伏发电因受天气和环境等因素的影响，导致光伏发电出力存在一定的波动性和不确定性^[7-8]。基于此，为了确保电网运行的安全性，提高电网的经济性，国内外学者已经提出了多种将不确定性因素纳入其中的电网规划和调度方法^[9-10]。近年来，光伏发电的点预测模型成为研究的热点。从预测方法上讲，点预测方法主要分为物理研究法^[11]和统计研究法。物理法主要是将数值天气预报信息和分布式光伏电站详细的地理地貌信息相结合，预测精确度主要受天气预报准确性的影响。文献[12]将气象信息的时间变化纳入到时间序列中，提出了一种新的混合预测方法。统计法是建立在对光伏发电的历史统计数据的基础上，通过数据训练、曲线拟合等方法构建光伏发电系统和影响因素的关系。常见的方法有神经网络法^[13]、支持向量机^[14]、时间序列预测法^[15]等。然而，由于光伏功率受气象因素影响导致的波动性和不平稳性，点预测模型难以全面描绘功率变化特征。

为了对电网调度、可靠性评估等决策提供理论依据，同时为光伏出力的波动性提供新的定量分析，研究者们日益关注区间预测方法。区间预测是一种对光伏发电不确定性造成的预测结果偏差进行量化的强大工具，它在给出点预测结果的同时，还勾勒出了光伏发电功率波动的区间。文献[16]对时间序列数据二次分解处理后再进行预测，提升了一次分解中高频部分的预测准确率，但是所产生的子分量数目太多，单独进行预测所需的时间比较长。文献[17]提出了一种利用极限学习机与蒙特卡洛方法相结合的风力发电功率区间预测方法，取得了较好的预测效果。文献[18]提出一种基于信息熵变权区间组合和边界逼近的短期光伏功率区间预测方法。然而在不同的情形下，光伏出力的真实概率分布形状会有很大的差别，因此仅仅使用固定形状的先验分布很难达到精确建模。文献[19]提出一种将二次模态分解和深度学习相结合的短期风电功率区间预测方法，通过预测结果对比，说明完备集合经验模态分解比变分模态分解在功率信号分解上更有优势。文献[20-22]从不同的研究角度，对光伏功率区间预测的方法进行了研究，但是鲜有针对降低原始光伏功率序列的波动性、随机性来提升光伏功率区间预测的精准度的方法。

鉴于以上方法的不足，本文提出了一种基于自适应噪声完备集合经验模态分解(complete ensemble empirical mode decomposition with adaptive noise，CEEMDAN)和麻雀搜索算法优化的最小二乘支持向量机(sparrow search algorithm-least square support vector machine，SSA-LSSVM)分布式光伏功率区间预测模型。通过实例验证，本文所提区间预测模型相比其他多个方法具有更高的预测准确性。

1 光伏功率分解和重构

1.1 光伏历史出力数据相关性分析

为了从历史数据中抽取出所需的输入特性，在进行预测之前，必须先对这些数据进行相关性分析。文中所讨论的相关系数主要指在某个时间点上的输出功率与前若干天的同一时间点上的输出功率和当天前若干时间点上的输出功率之间的关系。因为本区域一整年的电力有效输出时段为08:00—18:00，共计11 h。所以，在分析数据时，只讨论这一时期的功率关系。本文选择了2018年6月1日到2018年6月31日的光伏功率历史数据，在每天的08:00—18:00，以15 min为间隔，对功率数据进行采样，获得了41个样本的功率值。

1）水平相关性

水平相关指要预测的功率点与前若干天同一时间的功率点之间的关系。将第 $i$ 天的功率值记为 $W_{i}$ ，第 $j$ 天的功率值记为 $W_{j}$ ，采用皮尔逊相关系数法，则任意2列的功率值的相关性计算公式为

P (W_{i}, W_{j}) = \frac{C o v (W_{i}, W_{j})}{σ_{W_{i}} σ_{W_{j}}} .

(1)

式中： $C o v (W_{i}, W_{j})$ 表示第 $i$ 天与第 $j$ 天功率的协方差； $σ_{W_{i}}$ 和 $σ_{W_{j}}$ 分别为各自功率的方差。

需要计算的水平相关性流程如下：

\{\begin{matrix} W = (W_{1}, W_{2}, \dots, W_{i}, \dots, W_{n})_{41 \times 365} \\ r_{i} = p_{i - s, i}, \dots, p_{i - 1, i}, i = 1, \dots, 365 \\ R = (r_{1}, r_{2}, \dots, r_{i}, \dots, r_{n - s})_{(365 - s) \times 5}^{T} \\ \bar{R_{j}} = \sum_{i = 1}^{365 - s} \frac{r_{i j}}{365 - s}, j = 1, \dots, s \end{matrix}

(2)

式中： $W_{i}$ 为41×1的向量；n为一年的天数，即365天；p_i_,_j 为任意2列数据的相关性大小； r_i 为第i天与前s天同一时刻功率的相关性向量。

2）垂直相关性

垂直相关分析指的是被预测的功率点与当天前若干时间点上的输出功率之间的关系，一天中一共有41个样本。按照天数排序，总共365天。第i列即为41个采样点中第i个采样点共计365天的数据，将 W 矩阵进行转置即可得到所需分析的数列 W_TRS。则垂直相关性的计算公式如下：

\{\begin{matrix} W_{T R S} = (W_{1}, W_{2}, \dots, W_{i}, \dots, W_{n})_{365 \times 41}^{T} \\ m_{i} = (o_{i - s, i}, \dots, o_{i - 1, i}), i = 1, \dots, 41 \\ R_{c} = (m_{1}, m_{2}, \dots, m_{i}, \dots, m_{41 - s})_{(41 - s) \times s}^{T} \\ \bar{R_{j}} = \sum_{i = 1}^{n - s} \frac{m_{i j}}{41 - s}, j = 1, \dots, s \end{matrix}

(3)

式中 m_i 为第i时刻与当天前s个时刻功率的相关性向量。

1.2 基于CEEMDAN和变分模态分解的光伏功率序列模态分解

1.2.1 CEEMDAN分解算法

考虑到经验模态分解(empirical mode decom-position，EMD)存在模态混叠的因素，CEEMDAN是在EMD法的基础上对其进行改进，并借鉴了EEMD法中加入高斯型噪声及采用多次迭加求平均的方法消除噪声的思路。相比集合经验模态分解(ensemble empirical mode decomposition，EEMD)算法，自适应噪声完备集合经验模态分解有效地减少了信号重建的误差并使分解的效率得到改善。CEEMDAN具体流程如下：

1）将待分解信号 $X (t)$ 添加k次均值为0的高斯白噪声，构造共k次实验的待分解序列 $X_{i} (t)$ ，其中i=1,2,3,…,k。

X_{i} (t) = X (t) + ε δ_{i} (t)

(4)

式中： $ε$ 为高斯白噪声权值系数； $δ_{i} (t)$ 为第i次处理时产生的高斯白噪声。

2）对上述序列 $X_{i} (t)$ 进行EMD分解，分解得到第1个模态分量(intrinsic mode functions，IMF)并取其均值作为CEEMDAN分解得到的第1个IMF。

\{\begin{array}{l} {I_{M F}}_{1} (t) = \frac{1}{k} \sum_{i = 1}^{k} I_{M F}_{1}^{i} (t) \\ r_{1} (t) = X (t) - {I_{M F}}_{1} (t) \end{array}

(5)

式中： ${I_{M F}}_{1} (t)$ 为CEEMDAN分解得到的第1个模态分量； $r_{1} (t)$ 为第1次分解后的余量信号。

3）将分解后得到的第j阶段余量信号添加特定噪声后，继续进行EMD分解。

\{\begin{array}{l} {I_{M F}}_{j} (t) = \frac{1}{k} \sum_{j = 1}^{k} E_{1} {r_{j - 1} (t) + ε_{j - 1} E_{j - 1} [δ_{1} (t)]} \\ r_{j} (t) = r_{j - 1} (t) - {I_{M F}}_{j} (t) \end{array}

(6)

中： $E_{j - 1} (\cdot)$ 表示对序列进行EMD分解后的第j-1个IMF分量； $ε_{j - 1}$ 表示CEEMDAN对第j-1阶段余量信号加入噪声的权值系数。

4）如果满足EMD停止条件，第n次分解的余量信号r_n (t)为单调信号，则迭代停止，CEEMDAN算法分解结束。

1.2.2 变分模态分解算法

由于CEEMDAN分解得到的IMF分量中存在高频非平稳分量，若对此分量直接进行预测会产生较大的误差，二次分解将一次分解得到的高频非平稳分量分解为具有周期性、较为平稳的分量，有助于改善其平稳度，提升预测精度。各分量的样本熵越大，表示信号越不平稳，对熵值最大的分量进行二次分解。

在变分模态分解(variational mode decomposition，VMD)中，泛函指的是VMD约束变分模型，而要求的极值就是每个模态分量中心频率的带宽之和最小。

构造出来的VMD约束变分模型如下：

\{\begin{array}{l} \underset{{u_{k}}, {w_{k}}}{m i n} {\sum_{k} {‖\partial_{t} {[δ (t) + \frac{j}{π t}] * u_{k} (t)} e^{- j w_{k} t}‖}_{2}^{2}} \\ s . t . \sum_{k} u_{k} = f \end{array}

(7)

式中：{u_k }与{w_k }分别为VMD分解出来的k个子模态分量集合和其对应的中心频率集合； $\partial_{t}$ 为偏导运算符； $*$ 为卷积运算符； $δ (t)$ 为单位脉冲函数；f为待分解的信号。

加入惩罚项α、拉格朗日乘法算子λ，转变为非约束变分问题：

\begin{matrix} L = ({u_{k}}, {w_{k}}, λ) = \\ α \sum_{k} {‖\partial_{t} [(δ (t) + \frac{j}{π t}) * u_{k} (t)] e^{- j w_{k} t}‖}_{2}^{2} + \end{matrix}

{‖f (t) - \sum_{k} u_{k} {(t)}_{}^{2}‖}_{2}^{2} + [λ (t), f (t) - \sum_{k} u_{k} (t)]

(8)

采用交替方向乘子法对{u_k }与{w_k }寻优，达到所需精度则输出分解分量。

1.3 基于SE样本熵的光伏功率分量重构

样本熵是在近似熵的基础上改进得到的一种用于分析时间序列数据的统计量，用来描述时间序列的不规则度和复杂度，样本熵值越大，表示时间序列自身相似度越大，其复杂性随之越小。其计算公式为

S_{E} (m, r, N) = - l n [\frac{C_{m} (r, N)}{C_{m + 1} (r, N)}]

(9)

式中：m为嵌入维数，一般取1或者2；r为相似容限，通常取待计算数据方差的0.1~0.25倍，本文选择0.25倍； $C_{m} (r, N)$ 和 $C_{m + 1} (r, N)$ 分别为序列在相似容限r下匹配m和m+1个点的概率。

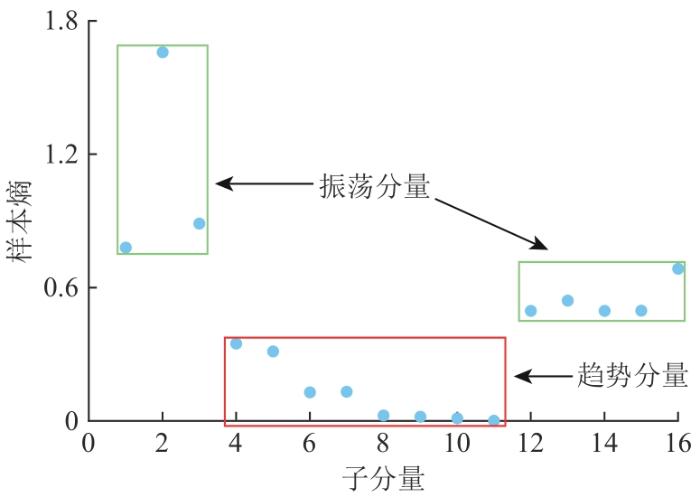
计算各分量的样本熵，将熵值大小划定范围并分类为趋势分量和振荡分量2类，最后分别对2类分量进行预测再相加得到最终预测值。趋势分量和原始分量波动规律十分贴近，包含了原始分量的绝大多数信息。振荡分量为一系列非平稳高频信号的叠加。通过分类能减少预测运行时间，提升预测精度。

2 基于SSA-LSSVM的优化预测模型

2.1 LSSVM模型

LSSVM是一种基于SVM的方法，它用等式约束来代替最优问题中的不等式约束，通过解决等式约束和最小二乘问题，可以进一步简化问题，提高问题的求解效率。

给定一组输入输出测试样本 $(x_{i}, y_{i}}_{i = 1}^{N}$ ,i=1, 2,…, N，其中 $x_{i} \in R$ 为输入， $y_{i} \in R$ 为输出。其回归函数为

y (x) = ω^{T} φ (x) + b

(10)

式中： $ω$ 为权值向量； $b$ 为偏差； $φ (x)$ 为对训练样本的非线性变换。

针对局部特异点的问题，对每个样本引入一个误差变量 $e_{i}$ ，并将该误差变量的正则项添加到原函数中。于是，关于LSSVM的最优解问题变为

\{\begin{array}{l} \underset{ω, b, e}{m i n} J (ω, e) = \frac{1}{2} ω^{T} ω + \frac{λ}{2} \sum_{i = 1}^{N} e_{i}^{2} \\ s . t . y_{i} = ω^{T} φ (x_{i}) + b + e_{i} \end{array}

(11)

式中 $λ$ 为正则化系数。

列出拉格朗日函数，则原问题可以转化为对拉格朗日乘数 $α_{i}$ 求极值的问题：

L (ω, b, e, α) = J (ω, e) - \sum_{i = 1}^{N} α_{i} [ω^{T} φ (x_{i}) + b + e_{i} - y_{i}]

(12)

对式(12)中参数 $ω, b, e_{i}, α_{i}$ 分别进行偏微分处理，使其为0，解方程组可得其回归函数为

y = \sum_{i = 1}^{N} α_{i} k (x_{i}, x) + b

(13)

其中 $k (x_{i}, x)$ 为核函数，其公式为

k (x_{i}, x) = e x p (- \frac{x_{i} - x_{j}}{2 σ^{2}})

(14)

核函数 $σ$ 和正则化系数 $λ$ 是LSSVM的重要参数，关系到模型的抗干扰和泛化能力，本文采用SSA来对这2个参数进行寻优。

2.2 麻雀搜索算法

在SSA算法中，一般会把种群中的麻雀分成2类：一类是探索者，另一类是追随者，这两类麻雀的地位是不断改变的。另外，麻雀会根据初始位置和适应度值在迭代中更新自己的位置和身份。

2.2.1 探索者位置更新

在觅食的同时，所有个体均会对周围环境保持警惕以防天敌的到来。探索者会根据预警值 $R_{2}$ 和报警值 $S_{T}$ 来改变自己的位置。

X_{i, D}^{t + 1} = \{\begin{array}{l} X_{i, D}^{t} \cdot e x p (\frac{- i}{α \cdot N}), R_{2} < S_{T} \\ X_{i, D}^{t} + Q \cdot L, R_{2} \geq S_{T} \end{array}

(15)

式中： $X_{i, D}^{t + 1}$ 为第i只麻雀在D维中的位置； $t$ 为目前迭代次数； $N$ 为最大迭代次数； $α \in [0,1]$ ； $R_{2} \in [0,1]$ ； $S_{T} \in [0,1]$ ； $Q$ 为服从正态分布的随机数； $L$ 为一个 $1 \times D$ 的矩阵，其中每个元素均为1。当 $R_{2} < S_{T}$ 时，意味着周围没有天敌，探索者可以进行全局搜索；当 $R_{2} \geq S_{T}$ 时，说明有天敌在附近，他们必须去其他地方寻找食物。

2.2.2 追随者位置更新

在觅食过程中，一些追随者会时刻监视着探索者，它们会与监视者争夺食物。其位置更新方式如下：

X_{i, j}^{t + 1} = \{\begin{array}{l} Q \cdot e x p (\frac{X_{w o r s t}^{t} - X_{i, j}^{t}}{i^{2}}), i > \frac{n}{2} \\ X_{p}^{t + 1} + |X_{i, j}^{t} - X_{p}^{t + 1}| \cdot A^{+} \cdot L, 其他 \end{array}

(16)

式中： $X_{p}^{t + 1}$ 为第 $t$ +1次迭代时最优探索者的位置； $X_{w o r s t}^{t}$ 为第 $t$ 次迭代时全局最差位置； $n$ 为种群规模； $A^{+}$ 为一个 $1 \times D$ 的矩阵，每个元素随机幅值为1或-1。当 $i > \frac{n}{2}$ 时，表明适应度值较低的第 $i$ 个追随者状态较差，需要飞往其他地方觅食。

2.2.3 警戒者位置更新

警戒者时刻关注着周围情况，其位置更新方式为

X_{i, j}^{t + 1} = \{\begin{array}{l} X_{b e s t}^{t} + β \cdot |X_{i, j}^{t} - X_{b e s t}^{t}|, f_{i} > f_{g} \\ X_{i, j}^{t} + K (\frac{|X_{i, j}^{t} - X_{w o r s t}^{t}|}{(f_{i} - f_{w}) + ε}), f_{i} = f_{g} \end{array}

(17)

式中： $X_{b e s t}^{t}$ 为第 $t$ 次迭代时全局最优位置； $β$ 为步长控制参数，其值为服从均值为0、方差为1的正态分布的随机数； $K$ 为 $[- 1,1]$ 内一随机数； $f_{i}$ 为麻雀个体适应度值， $f_{g}$ 、 $f_{w}$ 分别为当前最优、最差适应度值；当 $f_{i} > f_{g}$ 时，表示此麻雀处于群体边缘，为躲避危险会向种群中心集中；当 $f_{i} = f_{g}$ 时，说明种群中的麻雀对威胁有所警觉，为了躲避天敌，它们必须和同伴靠近以避免危险。

采用SSA对LSSVM的超参数进行优化，提升模型运行速度，具体预测步骤如下：

1）初始化SSA算法的参数：麻雀种群数量、探索者和追随者之间比例、优化变量大小的上下限、最大迭代次数等。

2）输入数据集，划分训练集和测试集，计算SSA算法个体适应度，保存最优个体及最优位置。

3）若在满足了终止迭代条件的情况下，可以确定最优解，退出程序；否则返回步骤2）。

4）将寻优得到的参数重新赋值给LSSVM，对网络进行训练，得到优化后的结果。

3 基于核密度估计的分布式光伏出力区间预测

3.1 核密度估计

核密度估计(kernel density estimation，KDE)作为一种非参数估计方法，无需使用历史数据已知的分布，并对数据的分布进行假设，可以直接从数据自身取样获取对应的预估周期的分布。核密度估计的计算公式为

\hat{f_{d}} (x) = \frac{1}{N d} \sum_{i = 1}^{N} K (\frac{T_{i} - x}{d})

(18)

式中： $d$ 为带宽； $N$ 为分位数总数； $T_{i}$ 为由条件分位数构成的数据集； $K (\cdot)$ 为核函数； $\overset{\land}{f_{d}} (x)$ 为带宽为 $d$ 时的核密度表达式。

由于核函数的选择会对估计结果产生一定的影响，本文采用gaussian核函数，此函数均方误差较小，预测精度较高，公式为

K (x; h) = e x p (- \frac{x^{2}}{2 h^{2}})

(19)

通过核密度估计方法计算得到振荡分量的误差概率密度函数，对其求积分，得到 $\hat{F_{d}} (x)$ 概率分布函数。在显著性水平为 $α$ 下，若误差样本落入误差区间 $[ε_{l o w}, ε_{h i g h}]$ 的概率不低于 $1 - α$ ，则把区间 $[ε_{l o w}, ε_{h i g h}]$ 称为置信度为 $1 - α$ 的置信区间。将振荡分量的误差置信区间与趋势分量和振荡分量的点预测值进行叠加，得到最终的预测区间，计算公式如下：

p_{u b} = \{\begin{array}{l} p_{p r e} + ε_{h i g h}, p_{p r e} + ε_{h i g h} < p_{e} \\ p_{e}, p_{p r e} + ε_{h i g h} \geq p_{e} \end{array}

(20)

p_{l b} = \{\begin{array}{l} p_{p r e} + ε_{l o w}, p_{p r e} + ε_{l o w} > 0 \\ 0, p_{p r e} + ε_{l o w} \leq 0 \end{array}

(21)

式中： $p_{u b}$ 为预测区间上限； $p_{l b}$ 为预测区间下限； $p_{p r e}$ 为趋势分量和振荡分量叠加的点预测值； $p_{e}$ 为光伏额定功率。

3.2 分布式光伏出力点预测模型

传统的点预测方法总会与真实值之间产生差异，然而分布式光伏发电系统的功率输出有着明显的概率分布特征。光照强度对光伏发电功率有直接的影响，比如在晴天、多云、阴天、雨雪4种典型的天气状态下，光伏出力有着显著的差别。

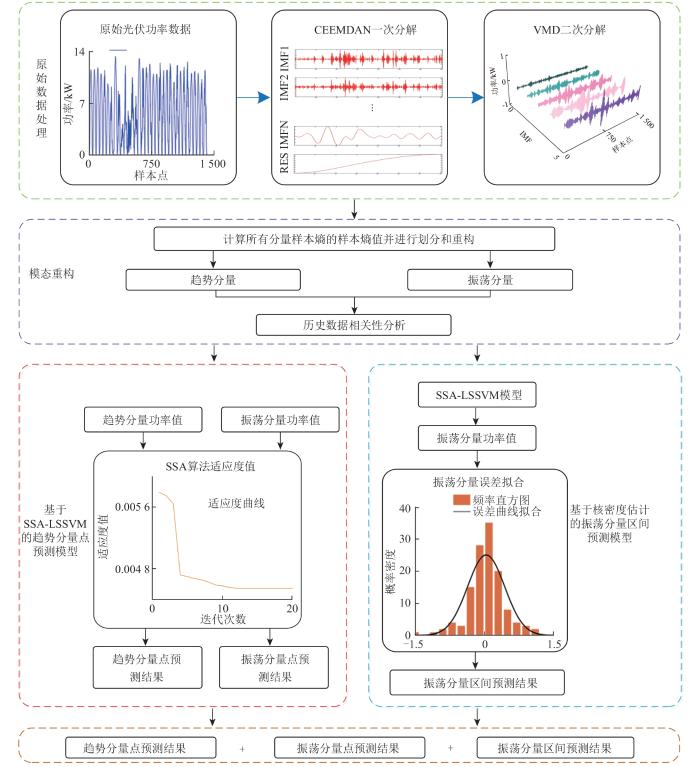
本文将CEEMDAN模态分解算法与LSSVM模型相结合，提出了一种基于CEEMDAN-SSA-LSSVM的分布式光伏功率点预测模型。具体预测流程如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 区间预测方法流程图

Fig. 1 Flow chart of interval prediction method

1）功率数据预处理，首先提取08:00—18:00有出力功率时段的数据，然后再排除不正常的数据，补全缺失的数据等，最后对历史数据进行相关性分析，得到模型的输入特征。

2）采用CEEMDAN算法将光伏功率序列进行分解，得到共计K个具有不同特征、频率互异的 $I M F$ 分量。

3）通过计算各 $I M F$ 分量的样本熵值，将样本熵值最大，即频率最高、最不稳定分量二次分解为N个子分量。

4）根据样本熵值的大小，熵值大小相近的聚为一类，将多个 $I M F$ 分量重构为振荡分量和趋势分量。

5）整理LSSVM预测模型的输入输出序列，并划分训练集和测试集；初始化SSA算法的参数，包括种群个数、探索者与追随者之间比例、迭代次数。对LSSVM的2个参数(核函数和正则化系数)进行寻优，并重新赋值给LSSVM模型。

6）利用寻优好的LSSVM模型分别对趋势分量和振荡分量进行预测，2组预测结果叠加得到最终点预测结果。

3.3 分布式光伏出力区间预测模型结构

针对不同天气因素影响所带来的功率波动以及单一的点功率预测模型不能反映功率波动的局限性，本文在点预测模型的基础上加入核密度估计方法，提出一种基于CEEMDAN-SSA-LSSVM的分布式光伏功率区间预测模型。此模型可有效提升预测的可靠性，反映预测算法的全面性，在一定程度上能提升功率预测精度，减少人工寻优时间。

首先，在分布式光伏出力点预测阶段，采用寻优能力强、收敛速度快的SSA对LSSVM模型进行优化，得到趋势分量和振荡分量点预测值；然后，在分布式光伏出力区间预测阶段，采用KDE对振荡分量的点预测误差进行概率密度估计，得到误差置信区间。振荡分量区间预测结果与趋势分量和振荡分量点预测值叠加，得到整体的区间预测结果。

4 算例分析

4.1 数据处理与误差评价指标

4.1.1 输入特征选取

本文基于江苏省某地2018年6月1日到6月31日的历史光伏数据进行算例分析。考虑到全年光伏有明显出力时段为08:00—18:00，以15 min为间隔，对功率数据进行采样，并对异常数据进行剔除以及补充缺失数据。

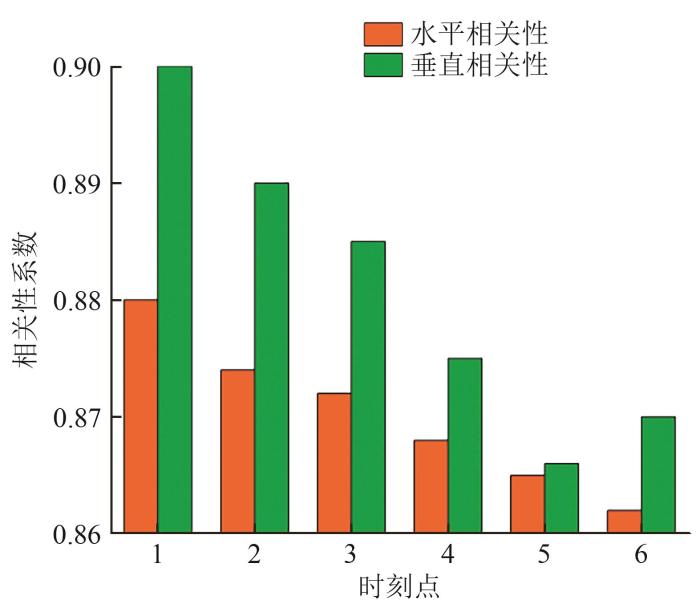
通过水平相关性和垂直相关性计算公式，分别得到某时刻的输出功率与前6天同一时间点上的输出功率和当天前6个时间点上的输出功率之间的相关性，如图2所示。可以看出，某时刻的功率与历史时刻的功率之间存在着很强的关联度，相关性系数均在0.86以上，且在水平和垂直方向上与最近的3个时间点关联程度较大。根据综合考虑，添加前3天的 $t - 3 、 t - 2 、 t - 1 、 t$ 时刻功率，当天 $t - 3 、 t - 2 、 t - 1$ 时刻功率共计15个特征作为输入。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 水平和垂直相关性系数

Fig. 2 Horizontal and vertical correlation coefficient

4.1.2 点预测误差评价指标

本文采用不同指标对模型性能从多方面进行评价，包括均方根误差(root mean square error，RMSE)、均方误差(mean square error，MSE)、平均绝对误差(mean absolute error，MAE)、平均绝对百分比误差(mean absolute percentage error，MAPE)、拟合优度R²。前4个变量越接近0，第5个变量越接近1，表示预测效果越好。具体公式如下：

\{\begin{array}{l} e_{R M S E} = \sqrt[]{\frac{1}{m} \sum_{i = 1}^{m} [h (x_{i}) - y_{i}]^{2}} \\ e_{M S E} = \frac{1}{m} \sum_{i = 1}^{m} [(h (x_{i}) - y_{i}]^{2} \\ e_{M A E} = \frac{1}{m} \sum_{i = 1}^{m} |h (x_{i}) - y_{i}| \\ e_{M A P E} = \frac{100 %}{m} \sum_{i = 1}^{m} |\frac{h (x_{i}) - y_{i}}{y_{N}}| \\ R^{2} = 1 - \frac{\sum_{i = 1}^{m} [h (x_{i}) - y_{i}]^{2}}{\sum_{i = 1}^{m} (y_{i} - y_{m})^{2}} \end{array}

(22)

式中： $h (x_{i})$ 为模型预测值； $y_{i}$ 为真实值； $y_{N}$ 为额定装机容量； $y_{m}$ 为测试集数据平均值； $m$ 为测试集样本数量。

4.1.3 区间预测误差评价指标

预测区间覆盖率 $ε_{P I C P}$ 和预测区间平均宽度 $ε_{P I N A W}$ 是评估区间预测方法的重要指标。预测区间覆盖率表现为预测区间所能包含实际功率点的个数。当预测区间宽度足够宽时，区间覆盖率会产生全覆盖的情况，这样并不能对分布式光伏功率进行合理的预测。通过引入预测区间平均宽度能够保证模型的有效性。具体公式如下：

ε_{P I C P} = \frac{f}{m} \times 100 %

(23)

ε_{P I N A W} = \frac{1}{m} \sum_{i = 1}^{m} \frac{p_{u b} - p_{l b}}{y_{m a x} - y_{m i n}}

(24)

式中： $f$ 为实际值在预测区间内的数目； $y_{m a x}$ 为测试集数据最大值； $y_{m i n}$ 为测试集数据最小值。

4.2 功率序列模态分解与重构结果

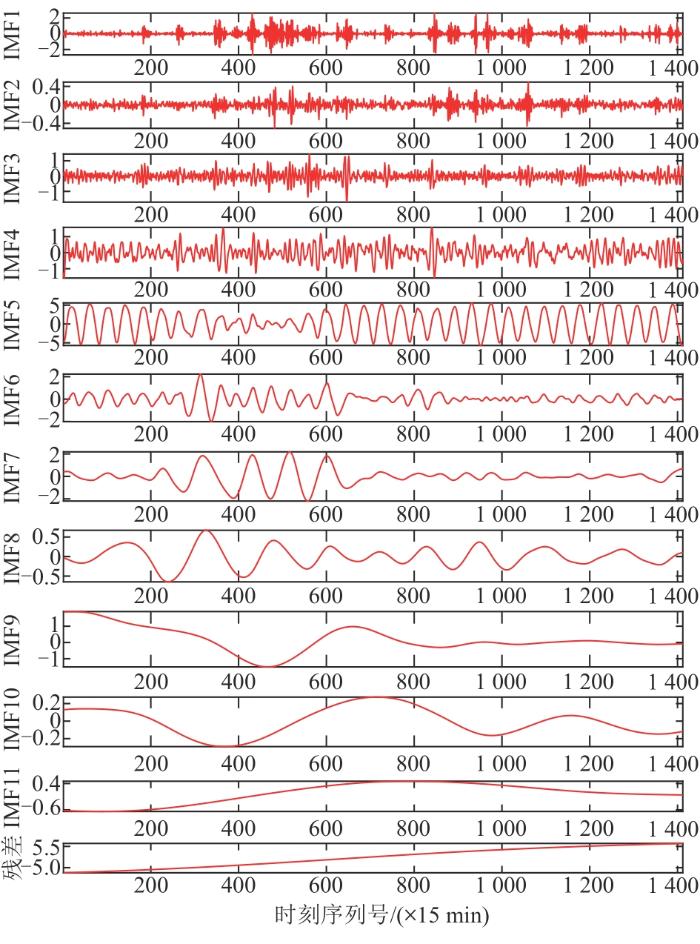
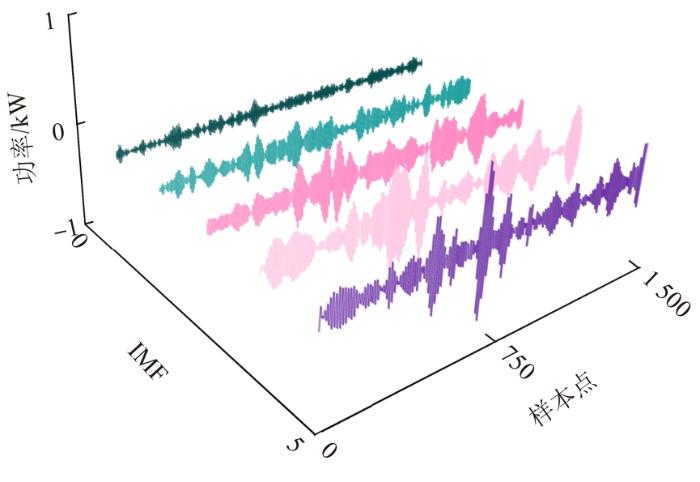
利用CEEMDAN对原有的分布式光伏出力数据进行分解，得到11个固定模式的子成分和1个残差成分，分解结果如图3所示。通过对这12个子项进行样本熵的计算，分析它们的复杂度。采用VMD对熵值最大的分量3(IMF3)进行二次分解，得到5个固定模态子分量和1个残差分量，5个固定模态子分量分解结果如图4所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 CEEMDAN一次分解结果图

Fig. 3 CEEMDAN single decomposition result chart

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 VMD二次分解结果图

Fig. 4 VMD secondary decomposition result diagram

2次分解得到的16个分量的样本熵值如图5所示，可知，子分量4—11的样本熵值较为接近，且熵值均分布在0~0.5，分量较为平稳，可以将其重构为一个分量来进行预测。这些分量重构得到的分量能大致反映原始序列的波动趋势，故称此重构的分量为趋势分量。同理，子分量1—3、12—16样本熵值较为接近，将其重构为振荡分量，重构结果如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 样本熵重构结果

Fig. 5 Sample entropy reconstruction results

4.3 点功率预测结果

对趋势分量和振荡分量分别进行预测，最后叠加得到模型预测结果。实验中，SSA-LSSVM模型的最优超参数设置如下：麻雀种群数量为10，最大迭代次数为50次，核函数 $σ$ 和正则化系数 $λ$ 的寻优范围均设置为[1, 10 000]，适应度目标函数为均方误差最小值。采用SSA优化，最终得到LSSVM的最优参数为σ=360，λ=1 286。

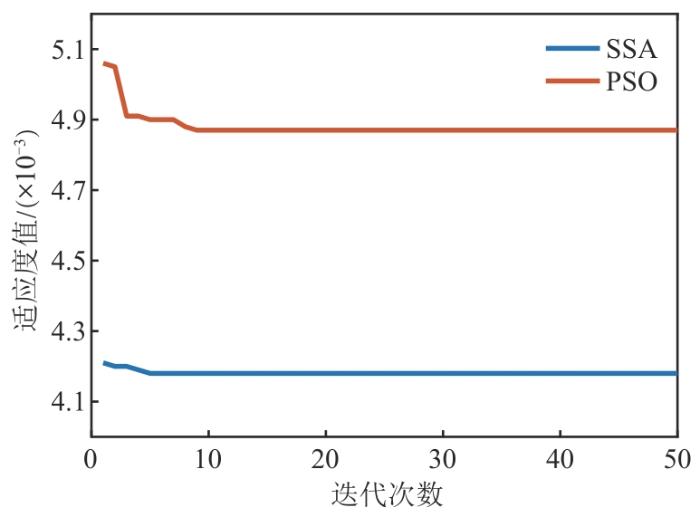
分别选取粒子群优化(particle swarm optimization，PSO)算法和SSA算法对LSSVM参数进行寻优，2种算法分别运行50次后的平均适应度曲线如图6所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 PSO与SSA迭代收敛对比图

Fig. 6 Comparison chart of PSO and SSA iteration convergence

从图6可知，SSA算法的平均最优适应度值收敛速度更快，模型运行时间更短。

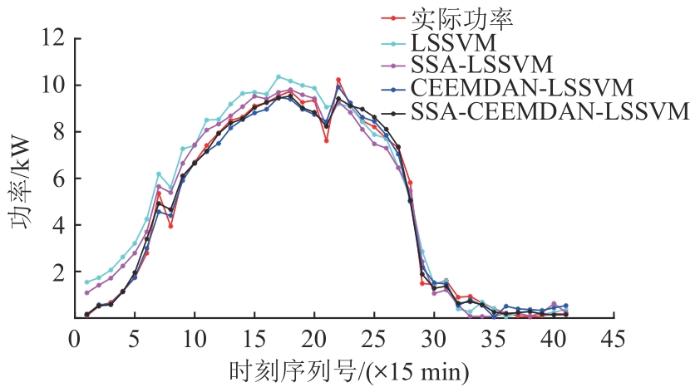
本文以前21天、前26天、前29天和前30天的数据作为训练集，将后10天、后5天、后3天和后1天的数据作为测试集进行仿真模拟。为凸显本文所提方法的预测效果，将LSSVM、SSA-LSSVM和CEEMDAN-LSSVM这3种方法与本文方法进行对比，利用RMSE、MSE、MAE、MAPE、R² 这5个指标进行综合评价。因为机器学习算法具有随机性，为了提高模型可信度，分别对以上4种模型进行5次预测仿真，取5次实验的平均值作为最终结果，4种模型的预测结果对比如图7、8所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 不同模型的点预测结果

Fig. 7 Point prediction results of different models

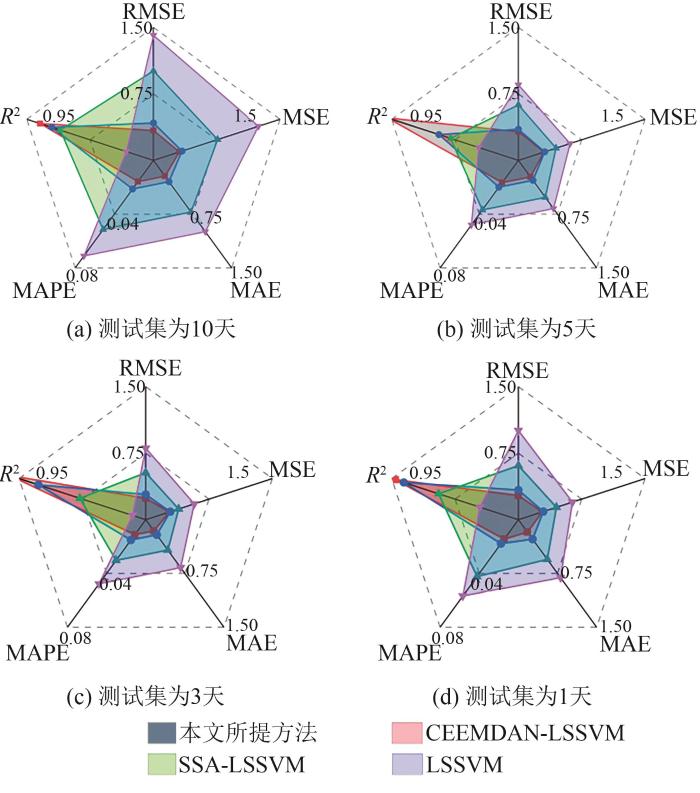
从图7可以看出，与其他预测模型相比，CEEMDAN-SSA-LSSVM模型的预测效果更好，预测曲线与真实值最为接近。由图8可以更直观地发现，相较于其他的预测模型，CEEMDAN-SSA-LSSVM模型的各项误差评价指标都优于其他模型。以测试集为1天的结果为例，相较于CEEMDAN-LSSVM、SSA-LSSVM、LSSVM方法，本文方法的RMSE分别降低了20.4%、66.69%、76.15%；MSE分别降低了36.63%、88.9%和94.3%；MAE分别降低了26.1%、69.49%和77.89%；MAPE分别降低了0.556%、3.571%和5.536%。本文方法拟合优度 $R^{2}$ 高达0.993 5，均优于其他3个模型。实验结果表明，本文所提方法预测效果极佳，具有较高的预测精度。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 不同测试集下各类模型预测指标雷达图

Fig. 8 Radar chart of various model prediction indicators under different test sets

4.4 区间功率预测结果

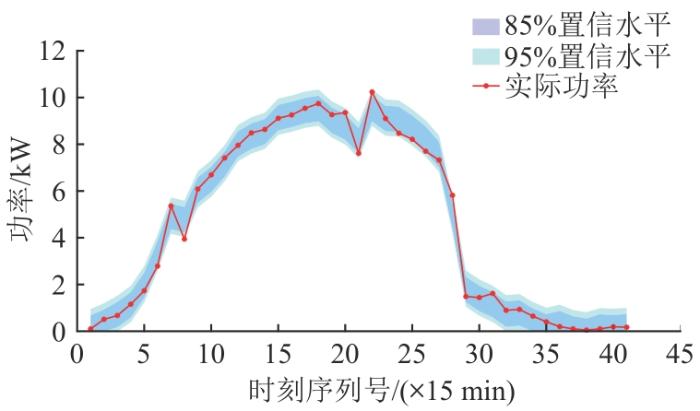
利用CEEMDAN-SSA-LSSVM的点预测结果，将振荡分量的预测值与真实值作差得到预测误差功率序列。通过核密度估计方法拟合预测误差序列，得到误差累计概率密度分布函数，给定置信度，与点预测结果结合得到区间预测结果。不同置信水平下的预测结果如图9所示。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 2种置信水平下光伏功率区间预测结果

Fig. 9 Prediction results of photovoltaic power interval under two confidence levels

由图9的结果可以得出，在置信度为95%时，光伏功率实际值有39个点落入置信区间内，说明本文所提方法在一定程度上可以提高区间预测的可靠性。

为了检验核密度估计对误差分布拟合的准确性，分别计算出CEEMDAN-SSA-LSSVM模型与蒙特卡洛法、Bootstrap重采样法结合后的预测区间覆盖率和预测区间平均宽度。表1为3种方法区间预测指标对比结果。

表1 不同方法区间预测指标对比

Tab.1 Comparison of interval prediction indicators using different methods

算法	置信度/%	$ε_{P I C P}$ /%	$ε_{P I N A W}$
Bootstrap	85	82.93	1.33
Bootstrap	95	87.80	1.71
蒙特卡洛法	85	85.36	1.231
蒙特卡洛法	95	90.24	1.667
本文方法	85	87.80	1.092 8
本文方法	95	95.12	1.554 0

新窗口打开| 下载CSV

从表1可以看出，在相同置信度下，相较于其他2种方法，本文所提CEEMDAN-SSA-LSSVM的区间预测模型，能够密切跟踪光伏功率序列的变化，并能够获得更高的预测区间覆盖率和更窄的预测区间平均宽度。在置信度为95%时，本文方法的预测区间覆盖率相较于其他2种方法分别提升了7.32%和4.88%；预测区间平均宽度也为最小，相较于其他2种方法分别降低了0.156和0.113。

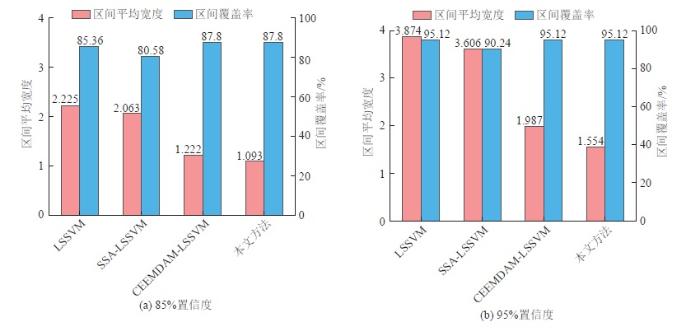
为了进一步证明本文提出模型的有效性，将本文区间预测方法与LSSVM、SSA-LSSVM和CEEMDAN-LSSVM方法进行对比，结果如图10所示。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 不同算法区间预测指标对比

Fig. 10 Comparison of interval prediction indicators for different algorithms

由图10可以发现，本文方法的在不同置信度下的准确度、可靠度都较为出色，预测区间均能得到较窄的区间宽度和较高的区间覆盖率。

5 结论

1）在分布式光伏功率数据处理中加入二次模态分解，再结合样本熵对其子序列进行重构，可有效降低原始预测分量的复杂程度的同时提升模型预测准确性。

2）所提核密度估计区间预测方法可以有效实现光伏功率区间预测，相较于其他传统预测模型，能够提升预测区间覆盖率的同时降低预测区间平均宽度。在置信度为95%时，所提方法的预测区间覆盖率相较于其他2种方法分别提升了7.32%和4.88%，预测区间分别降低了0.156和0.113。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

张汀荟，谢明成，王蓓蓓，等．

分布式光伏的共享价值及其对配电网影响的系统动力学仿真

[J]．电力系统自动化，2021，45(18)：35-44．