基于改进模糊C-均值聚类的陆上风电场集电线路回路划分与拓扑结构优化

doi:10.12096/j.2096-4528.pgt.23040

基于改进模糊C-均值聚类的陆上风电场集电线路回路划分与拓扑结构优化

易海¹, 吕宙安¹, 张伶俐¹, 陈希¹, 柳典¹, 黄雨薇², 韩星星², 许昌²

1.中国三峡新能源(集团)股份有限公司, 北京市西城区 101100

2.河海大学能源与电气学院, 江苏省南京市 211100

Onshore Wind Farm Collector Circuit Division and Topology Optimization Based on Improved Fuzzy C-Means Clustering

YI Hai¹, LÜ Zhouan¹, ZHANG Lingli¹, CHEN Xi¹, LIU Dian¹, HUANG Yuwei², HAN Xingxing², XU Chang²

1.China Three Gorges Renewables (Group) Co. , Ltd. , Xicheng District, Beijing 101100, China

2.College of Energy and Electrical Engineering, Hohai University, Nanjing 211100, Jiangsu Province, China

收稿日期: 2023-12-04 修回日期: 2024-02-20

基金资助:

国家自然科学基金项目.  52106238
三峡新能源科技项目.  2021-491
政府间双边创新合作项目.  BZ2021019

Received: 2023-12-04 Revised: 2024-02-20

作者简介 About authors

易海(1985)，男，高级工程师，主要从事新能源发电项目集电线路与送出线路工程优化设计及技术研究工作，yi_hai@ctg.com.cn；

许昌(1985)，男，博士，教授，主要从事风电场设计和运行优化方面的研究工作，本文通信作者，zhuifengxu@163.com。

摘要

目的在“双碳”目标以及我国能源结构加速转型的双重驱动下，风电产业规模不断快速增长，亟须降本增效以应对平价上网压力。集电线路的造价在投资中占比较大，存在可观的优化空间。为了降低投资成本，提出了一种改进模糊C-均值(fuzzy C-means，FCM)聚类算法。方法利用改进FCM聚类算法对陆上风电场集电线路回路进行划分。该算法综合考虑了方位角与欧式距离，以保障回路间线路不交叉，并使相邻机组聚集到同一回路；引入机位到聚类中心距离的修正因子，通过调节其数值限制回路容量。在回路划分的基础上，利用动态Prim算法对各回路进行集电线路优化选线。最后，通过某陆上风电场算例验证方法的有效性。结果与只考虑方位角的聚类方法相比，考虑方位角和间距的改进FCM算法优化效果更好，单回、双回连接对应的集电线路总造价分别降低了2.6%和5.4%。结论所提算法能够有效降低集电线路的总造价，具有一定的应用价值，可为风电场集电线路设计提供参考。

关键词： 陆上风电场 ; 集电线路 ; 拓扑结构优化 ; 模糊C-均值(FCM)聚类算法 ; 动态Prim算法

Abstract

Objectives Driven by the dual carbon goal and the accelerated transformation of China’s energy structure, the scale of the wind power industry continues to grow rapidly, and there is an urgent need to reduce costs and increase efficiency to cope with the pressure of grid parity. The cost of collector lines accounts for a relatively large proportion of investment, and there is considerable space for optimization. In order to reduce the investment cost, an improved fuzzy C-means (FCM) clustering algorithm was proposed. Methods The improved FCM clustering algorithm was used to divide the collector circuit of onshore wind farm. The algorithm comprehensively considered the azimuth angle and the Euclidean distance to ensure that the lines between the circuits were not crossed, and the adjacent units were gathered to the same circuit. The correction factor of the distance from the machine position to the cluster center was introduced, and the circuit capacity was limited by adjusting the distance correction factor. On the basis of circuit division, the dynamic Prim algorithm was used to optimize the line selection of each circuit. Finally, the effectiveness of the method was verified by an example of an onshore wind farm. Results Compared with the clustering method only considering the azimuth angle, the improved FCM algorithm considering azimuth angle and spacing has better optimization effect. The total cost of single-circuit and double-circuit collection lines is reduced by 2.6% and 5.4%, respectively. Conclusions The proposed algorithm can effectively reduce the total cost of collector lines, and has certain application value. It can provide a reference for the design of wind farm collector lines.

Keywords： onshore wind farm ; collector line ; topology optimization ; fuzzy C-means (FCM) clustering algorithm ; dynamic Prim algorithm

PDF (2581KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

易海, 吕宙安, 张伶俐, 陈希, 柳典, 黄雨薇, 韩星星, 许昌. 基于改进模糊C-均值聚类的陆上风电场集电线路回路划分与拓扑结构优化. 发电技术[J], 2024, 45(4): 675-683 DOI:10.12096/j.2096-4528.pgt.23040

YI Hai, LÜ Zhouan, ZHANG Lingli, CHEN Xi, LIU Dian, HUANG Yuwei, HAN Xingxing, XU Chang. Onshore Wind Farm Collector Circuit Division and Topology Optimization Based on Improved Fuzzy C-Means Clustering. Power Generation Technology[J], 2024, 45(4): 675-683 DOI:10.12096/j.2096-4528.pgt.23040

0 引言

在“碳达峰”和“碳中和”目标的促进下，我国风电产业持续蓬勃发展，亟须提高风电场设计和运维水平，以应对风电平价上网压力^[1-2]。集电线路的造价在发电成本中占比较大，为风电场总造价的15%~30%^[3]。作为风电场设计的重要组成部分，风电场集电线路拓扑结构优化设计对降低风电场投资、提升整体收益具有显著作用^[4]。传统的集电线路设计方法，一般是由设计人员根据经验确定风电机组间及其与升压站连接的拓扑结构并选择导线型号。该过程耗时长，设计效率低，在调整过程中需要反复计算集电线路造价，难以进行拓扑优化，其经济性无法保障。为了降低投资成本，应对风电平价上网压力，开展风电场集电线路拓扑结构优化研究具有重要意义。

风电场集电线路拓扑结构优化，一般是指在集电线路输送容量不超限、线路不交叉等约束条件下，确定合适的连接关系，用导线将机组所发电力输送到升压站，使集电线路造价达到最低。风电场集电线路拓扑结构优化属于非确定性多项式(non-deterministic polynomial，NP)问题，无法在多项式时间内给出精确的最优解，只能通过进化算法获取近似的优化解^[5-6]。为此，研究者采用遗传算法和粒子群等进化算法来优化风电场集电线路拓扑结构。符杨等^[7]以电缆造价最低为目标，建立经济性优化模型，采用单亲遗传算法对模型进行求解，以实际案例对放射形、环形2类结构的经济性进行优化，从中选取2种最优结构进行可靠性评估，结合经济性及可靠性的定量分析数据，给出每种方案的适用范围。Fischetti等^[8]提出基于混合整数线性规划的风电场集电线路设计方法，其中包括一个基本的混合整数线性规划模型和3种扩展模型，以提高风电场的经济效益。Dutta等^[9]提出一种聚类算法，与传统的径向或链式电缆布局方法相比，该算法降低了集电系统的功率损耗，提高了风电场的发电可靠性。然而，对于机组数目众多的大型风电场，上述算法所需计算量大，计算效率较低。

为了降低计算量，提高计算效率，Hou等^[10]将集电线路的拓扑结构视作动态最小生成树问题，利用集电线路单位造价随拓扑结构变化的特点，设计了一种动态Prim算法进行线路路径优化。该方法既可与回路划分方法相结合^[11-12]，也可单独使用^[13-14]。在与回路划分方法相结合时，为保障回路间线路不交叉，通常以机位到升压站的方位角作为回路划分的依据，采用聚类算法划分回路。这种方法忽略了机位间距对造价的影响，可能导致相距较远的2台机组因方位角较近而划分到同一回路，使集电线路造价提高。而在单独使用动态Prim算法时，为避免回路容量超限或线路交叉，其优化的结果可能出现以下问题：1）一部分风电机组因规避线路交叉或者容量超限而无法接入回路中；2）当回路容量已满，距离该回路较近的风电机组未被分配进去，而被分配到较远的回路，导致造价提高；3）当风电机组数目较多时，所有机位同时优化，导致优化算法运行时间较长。由此可见，动态Prim算法作为贪婪算法，在不预先划分回路时，其优化结果容易出现“短视”现象。

针对上述问题，本文基于模糊C-均值(fuzzy C-means，FCM)聚类算法^[15]进行改进，达到回路间集电线路不交叉、回路内部机位聚集不分散的目的，实现回路最大容量限制。在上述回路划分的基础上，考虑集电线路单位长度造价随集电线路拓扑结构改变而动态变化的特性，引入动态Prim启发式算法，实现经济性目标优化。最后通过算例验证，得出算法的适用条件，为工程应用提供参考。

1 基于改进FCM算法和动态Prim算法的陆上风电场集电线路优化方法

1.1 陆上风电场集电线路导线截面选型

陆上风电场集电线路的导线一般为架空线型式，按照经济电流密度来选择导线的截面^[16-17]：

S_{j} \geq \frac{P}{\sqrt[]{3} U I_{j} c o s ϕ}

(1)

式中：S_j为导线截面积；P为集电线路中风电机组的单机额定功率；U为集电系统的电压等级；I_j为经济电流密度； $c o s ϕ$ 为功率因素。

当集电线路的载流量超限时，选择允许载流量更大的集电线路型号。

1.2 基于方位角和欧式距离的改进FCM回路划分方法

由于传统的聚类方法计算距离时一般采用欧式距离，因此，只能获得空间上距离相近的块状结果，而非设计人员期望的以升压站为中心的放射状聚类结果，如图1所示。对此，可引入FCM聚类算法，以机位到升压站的方位角作为聚类依据，将回路划分成以升压站为中心的放射状分布型式^[18]。单纯按方位角聚类划分回路，可能会将距离回路内其他机位较远的机位划分到本回路，导致集电线路路径长度增加，从而提高集电线路造价。此外，在具体实现过程中，并没有对每个回路的风电机组容量进行明确限制，也没有明确的容量限制方法来解决聚类结果存在单条回路载流量超限的问题^[18]。

图1

新窗口打开| 下载原图ZIP| 生成PPT

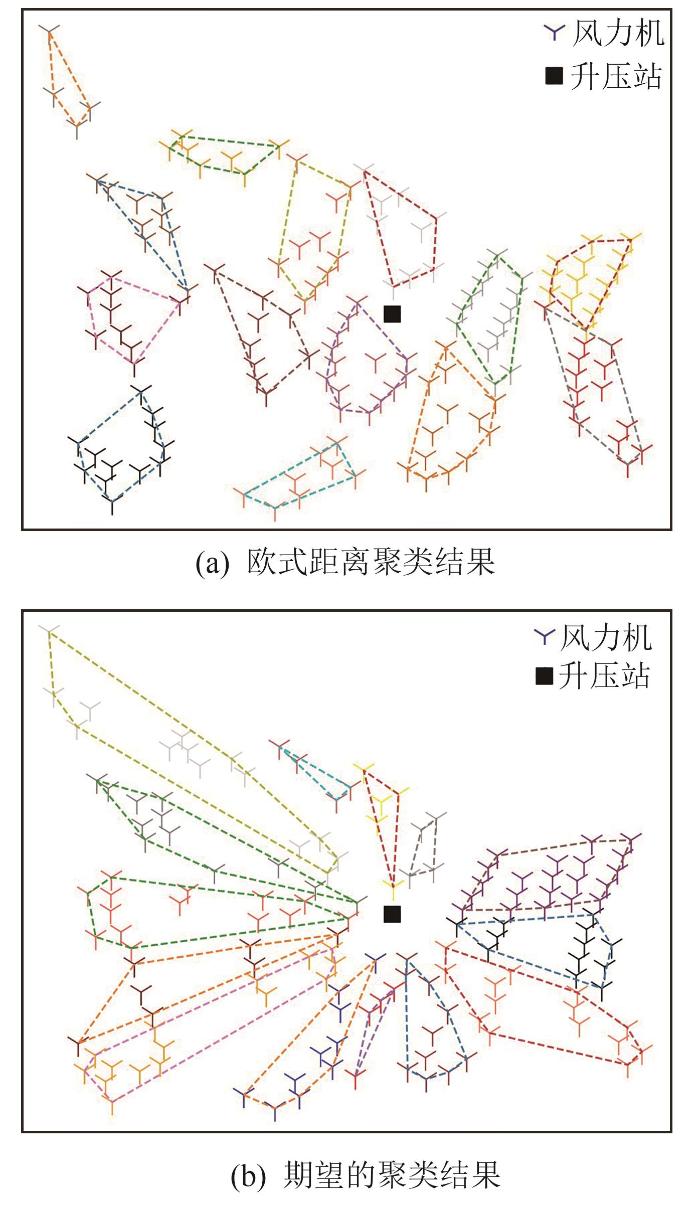
图1 欧式距离聚类结果和期望聚类结果对比

Fig. 1 Comparison of clustering results of Euclidean distance and expected clustering results

基于此，本文综合考虑方位角、机位与聚类中心的欧式距离，并引入聚类中心距离修正因子限制回路容量，提出基于方位角和欧式距离的改进FCM算法。与其他利用聚类划分回路的方法相比，该算法的优点在于：1）兼顾回路内机组方位角和间距，在保障回路间线路不交叉的前提下，使相邻机组划分到同一回路内，避免出现回路内机组间距过大的情况；2）引入聚类中心距离修正因子，用于修正回路内机组间距，在回路容量超限时，增加该修正因子，从而扩大回路内机组间距，使回路内部分机位在迭代过程中合并到其他回路，达到限定回路容量的目的。

FCM算法通过隶属度矩阵进行聚类，矩阵中元素值取0~1，表征机组归属于某个聚类中心的可能性。FCM算法的目标函数是使各台风电机组到各自聚类中心的综合距离加权和最小。聚类的过程是最小化目标函数的过程，当目标函数收敛时，即得到最终的聚类结果。目标函数表示如下：

J = \sum_{i = 1}^{N} \sum_{j = 1}^{C} u_{i j}^{m} d (x_{i}, c_{j})

(2)

式中：N为风电机组台数；C为划分的回路数； $d (x_{i}, c_{j})$ 表示各台风电机组到其聚类中心的方位角度差与欧式距离的加权综合距离； $c_{j}$ 表示第j个聚类中心； $x_{i}$ 表示第i台风电机组的坐标； $u_{i j}$ 表示风电机组 $x_{i}$ 对聚类中心 $c_{j}$ 的隶属度(即 $x_{i}$ 属于 $c_{j}$ 的概率，取值0~1)；m为隶属度矩阵的指数值，一般取常数2。

FCM算法的终止条件为前后2次隶属度 $u_{i j}$ 最大变化量的绝对值小于误差阈值 $σ$ ：

m a x | u_{i j}^{t} - u_{i j}^{t - 1} | < σ

(3)

式中：t为当前迭代步数； $σ$ 为一个很小的正数。

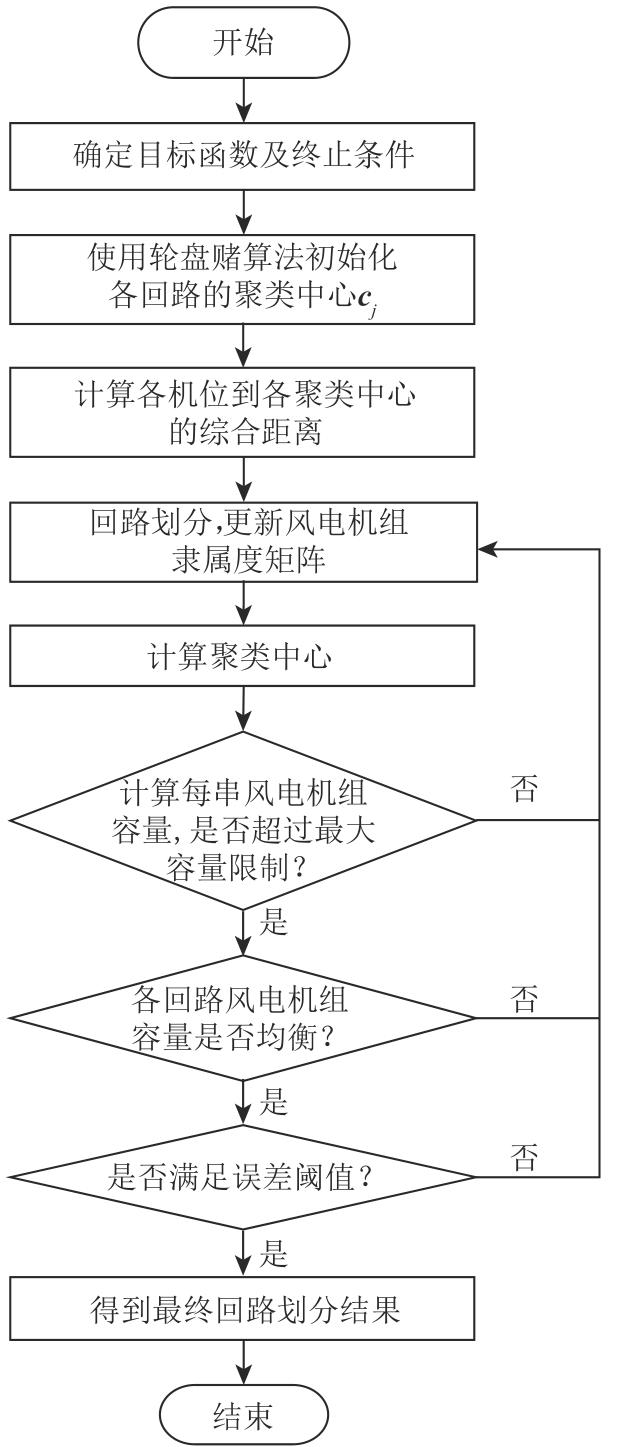
基于方位角和欧式距离的改进FCM回路划分算法流程如图2所示，具体步骤如下。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 考虑方位角和间距的改进FCM回路划分算法流程

Fig. 2 Improved FCM circuit division algorithm flow considering azimuth and spacing

1）使用不放回随机抽样方法，选择C个机位点经小距离随机偏移 $ε$ 后作为回路聚类中心 $c_{j}$ ，以使聚类中心均匀随机分布：

c_{j} = x_{i} + ε

(4)

2）计算各台机组到各聚类中心的综合距离：

d_{i j} = F_{j} \sqrt[]{k \cdot Δ θ_{i j}^{2} + (1 - k) {(\frac{‖ x_{i} - c_{j} ‖}{1.2 L_{r e f}})}^{2}} + ε_{1}

(5)

式中：F_j 为聚类中心距离修正因子，初始值为1；k为方位角与欧式距离的加权因子，其值在0~1，数值越大，说明方位角的占比越大； $Δ θ_{i j}$ 为机组-升压站-聚类中心的方位角夹角； $‖ x_{i} - c_{j} ‖$ 为机组 $x_{i}$ 到聚类中心 $c_{j}$ 的欧式距离； $L_{r e f}$ 为风电场机组间的参考距离，以机组 $x_{i}$ 到机组 $x_{j}$ 的直线段为边，生成连接各台机组的最小生成树，取最小树各边长的平均值(见图3)； $ε_{1}$ 是一个非常小的长度，防止聚类中心与某个机组重合，导致计算中分母出现0值。

图3

新窗口打开| 下载原图ZIP| 生成PPT

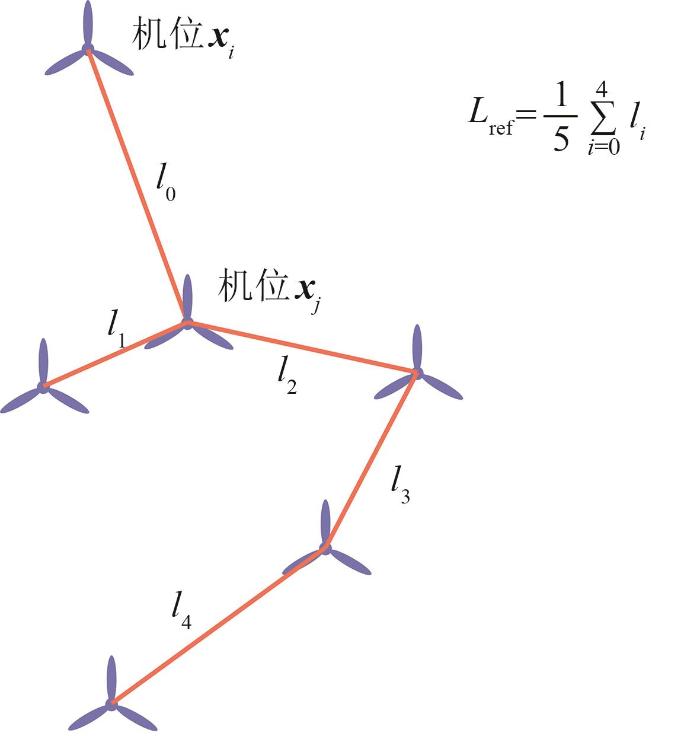
图3 连接各机组的最小生成树及机组参考间距

Fig. 3 Minimum spanning tree connecting each turbine and reference spacing between turbines

本文中方位角度差通过适用于方向数据的距离计算方法(见图4)^[19]得到，计算公式如下：

图4

新窗口打开| 下载原图ZIP| 生成PPT

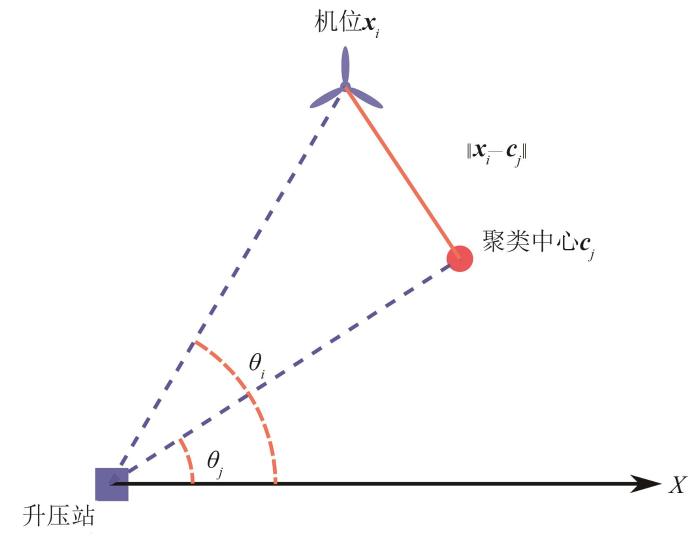
图4 适用于方向数据的距离计算方法示意图

Fig. 4 Schematic diagram of the distance calculation method suitable for direction data

Δ θ_{i j} = [(θ_{i} - θ_{j} + π) m o d (2 π)] - π

(6)

式中： $m o d (\cdot)$ 为求余函数； $θ_{i}$ 和 $θ_{j}$ 为需要计算的2个角度值，以升压站位置为极点，以正东方向引一条射线为极轴，取逆时针为正方向。

3）更新隶属度矩阵，将风电机组划分到与其相关最大隶属度对应的聚类中心。隶属度的计算公式如下：

u_{i j} = \frac{1}{\sum_{k = 1}^{C} {(\frac{d_{i j}}{d_{i k}})}^{\frac{2}{m - 1}}}

(7)

4）计算聚类中心：

c_{j} = \frac{\sum_{i = 1}^{N} u_{i j}^{m} x_{i}}{\sum_{i = 1}^{N} u_{i j}^{m}}

(8)

5）通过聚类中心距离修正因子F_j 对聚类结果进行容量过载检测。在每次迭代时，计算出每个回路连接的机组容量。如果回路中的风电机组容量超过最大容量，则增加距离修正因子F_j，使各机组到该聚类中心距离增大，降低该回路中机组的隶属度。当回路容量超限时，重复上述迭代过程，直到所有回路都没有出现过载现象为止。具体计算公式如下：

{F_{j}}^{t} = F_{j}^{t - 1} + \frac{C_{c l u s t e r}}{C_{m a x}}

(9)

式中： ${F_{j}}^{t}$ 、 $F_{j}^{t - 1}$ 分别为前后2次迭代所更新的距离修正因子； $C_{c l u s t e r}$ 为回路中的风电机组容量； $C_{m a x}$ 为回路最大允许容量。

6）判断前后2次隶属度最大变化值是否小于误差阈值 $σ$ 。如果小于 $σ$ ，则聚类结束，返回风电机组回路划分结果；否则返回步骤2），重新进行回路划分计算。

1.3 基于动态Prim算法的集电线路优化算法

风电场集电线路的拓扑结构对应一棵有向树T，树的顶点表示风电机组或升压站，树的边是连接风电机组与升压站的集电线路，边的方向为电能输送方向。由于集电线路单位长度的造价与其输送容量有关^[20]，在这棵树的生成过程中，每当向树中加入一条新边时，引入新边的顶点到升压站路径上各边的输送容量及其对应的线路造价可能会发生变化。集电线路造价与回路输送容量的关系^[20]如表1所示。表1中24 MW和48 MW分别为35 kV陆上风电场架空线(最大导线截面积为240 mm²)按经济电流密度计算时，单回路和双回路的最大允许输送容量。

表1 集电线路造价

Tab. 1 Collector line construction cost

输送容量/MW	≤8	≤16	≤24	≤48
造价/(万元/km)	25	30	35	45

新窗口打开| 下载CSV

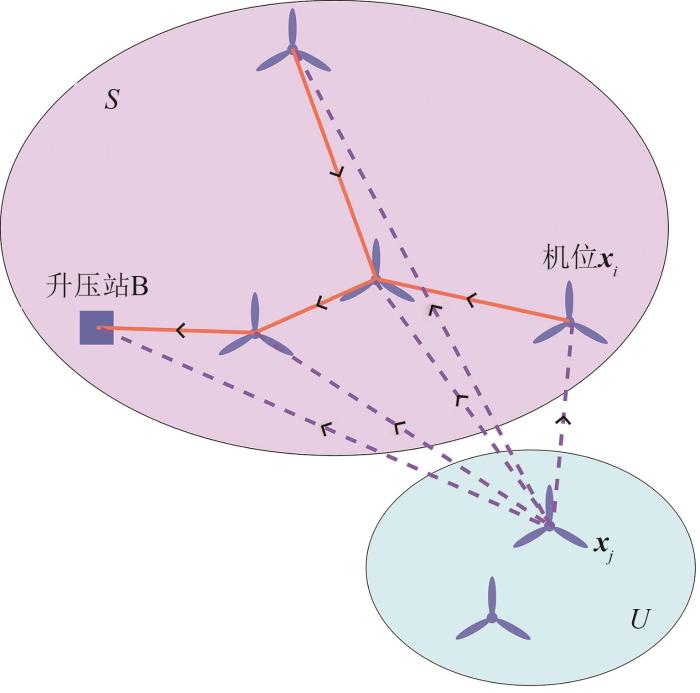
传统Prim算法设定树的边造价为固定值，未考虑树的拓扑结构改变时边造价的动态变化，对集电线路拓扑结构优化效果不佳。对此，本文引入动态Prim算法实现回路划分后风电场集电线路优化设计。以集合S表示有向树T的顶点集，集合E表示T的边集，集合U表示尚未加入T的机组集。采用动态Prim算法生成集电线路拓扑结构，如图5所示，具体步骤如下：

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 动态Prim算法生成集电线路拓扑结构示意图

Fig. 5 Schematic diagram of topological structure of collector lines generated by dynamic Prim algorithm

1）初始化。设置集合S中只包含升压站， $E = \emptyset$ ，机组编号组成集合U。

2）从集合U中任取一个顶点j与S中的任一点i相连，计算出连接i、j后生成树的新增造价 $C_{i j}$ 。在连接i、j时需确保连线不会与E中的边交叉，且连接后回路容量不超限，否则不进行新增造价。如果已经预先划分回路，则回路内只允许一台机组连接到升压站：当i表示升压站时，需判断升压站是否已与其他机组相连，如果相连，则不连接i、j。在本步骤中，若因线路交叉、超出容量限制等而无法产生新增造价 $C_{i j}$ ，则退出T的生成，返回当前T。

由于 $x_{j}$ 加入回路后，只影响其到升压站B最短路径( $p_{s} (x_{j} \to B)$ )中的边，因此可按式(10)计算新增造价：

\begin{matrix} Δ C_{i j} = \sum_{k = 1}^{K} l (e_{k}) \cdot c [P (e_{k}) + P] - \sum_{k = 1}^{K} l (e_{k}) \cdot \\ c [P (e_{k})] + ‖x_{i} - x_{j}‖ c P \end{matrix}

(10)

式中： ${e_{k} | k = 1,2, \dots, K}$ 为顶点i所在回路的边集， $e_{k} \in p_{s} (x_{j} \to B)$ ； $l (e_{k})$ 和 $P (e_{k})$ 分别表示边 $e_{k}$ 的长度以及其所承载的容量； $P$ 为 $x_{j}$ 所在机组的额定功率； $c$ 为集电线路造价(按表1设定)。

3）选择新增造价最小的边 $C_{i j}$ 加入生成树，将j从U中移除，移入S。

4）重复2）、3），直至无法向T中加入新边为止，返回最终的T。

2 风电场集电线路优化设计案例

2.1 优化案例参数

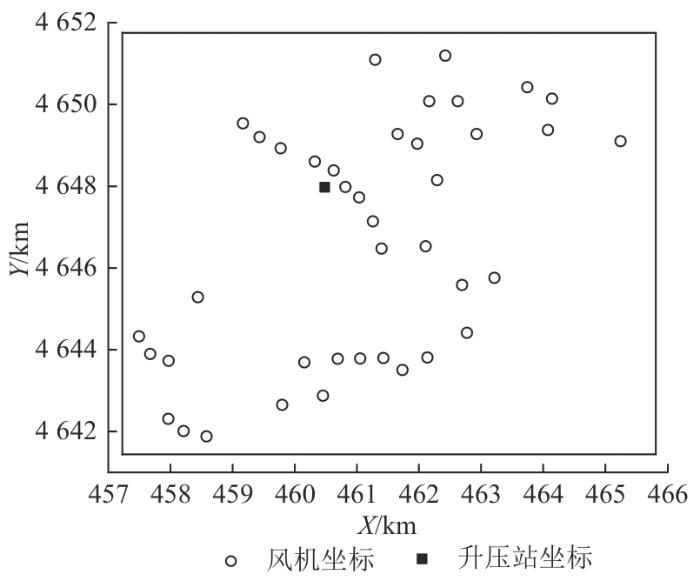
以辽宁某陆上风电项目为例，风电场大小为9 km×10.4 km，布置40台2.5 MW的风电机组。该风电场机组与升压站分布如图6所示，其中，黑色实线围成的矩形表示该风电场的边界。本文以人工经验设计作为对照，采用动态Prim算法、考虑方位角的FCM方法结合动态Prim算法，以及综合考虑方位角、间距的FCM方法结合动态Prim算法3种方法，对该风电场的集电线路进行优化设计，分析各方法的适用场景，并评估其优化效果。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 某已建成风电场机组与升压站分布图

Fig. 6 A completed wind farm machine and booster station distribution map

2.2 优化结果分析

1）人工经验设计

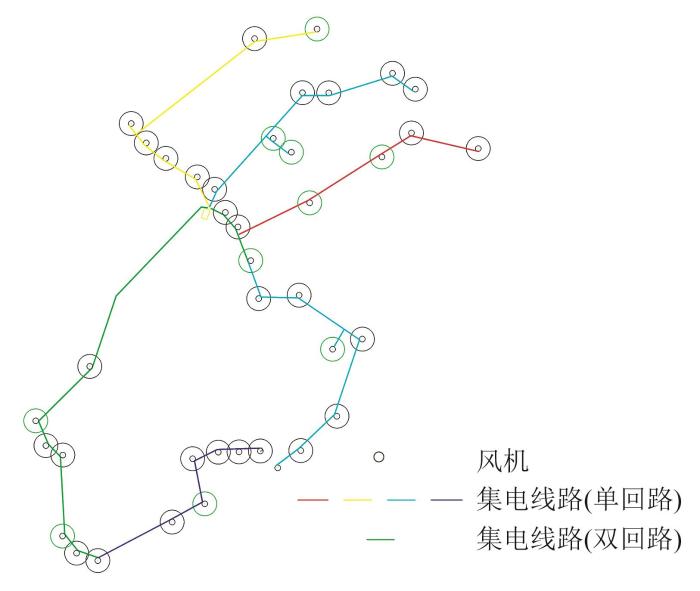
该方法主要根据升压站的位置以及风电机组分布情况手动布置集电线路，在保证不超出回路容量限制和线路不交叉的约束下手动划分回路，从风电场外围开始顺着机群走向连接机组，最终汇入升压站。人工经验设计的线路拓扑结构如图7所示。根据人工设计方案，本风电场采用单、双回路混合架设，线路路径全长约34 km，其中单回路线路路径长约23 km，双回路线路路径长约11 km，集电线路总造价约1 300万元。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 人工经验设计的线路拓扑结构

Fig. 7 Line topology designed by artificial experience

2）动态Prim算法

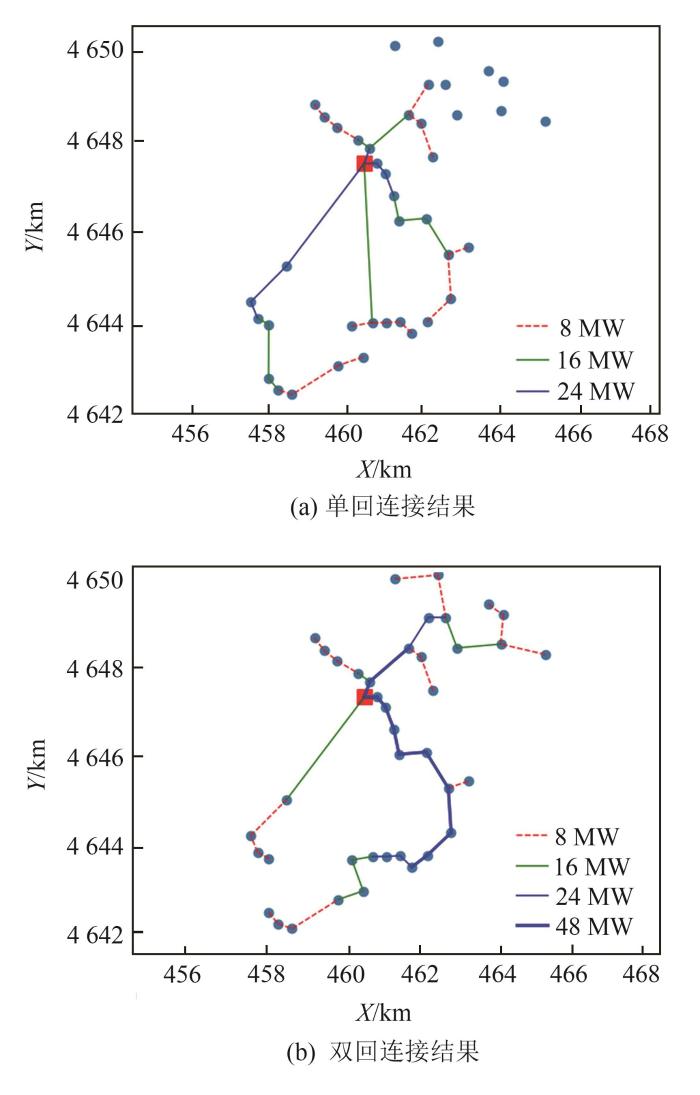
图8为采用动态Prim算法优化的线路拓扑结构。在采用单回连接方式，直接使用动态Prim算法优化集电线路拓扑结构时，有部分风电机组无法连接到回路中，变成“孤立状态”，明显不符合设计要求。在采用双回连接方式时，回路容量上限提高到48 MW，所有机组都能连接到回路中，经计算，此时线路造价为1 005.44万元。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 采用动态Prim算法优化的线路拓扑结构

Fig. 8 Line topology optimized by dynamic Prim algorithm

3）考虑方位角的FCM方法+动态Prim算法

采用只考虑方位角的FCM算法(加权因子k=1)对风电场回路进行划分，并结合动态Prim算法对各回路进行集电线路优化设计。根据回路容量限制的要求，本风电场回路数量在单回连接时设为5，在双回连接时设为3。采用该方法优化的集电线路拓扑结构如图9所示，单回、双回连接对应的集电线路系统总造价分别为1 079.30万元和1 122.04万元。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 考虑方位角的FCM方法优化的线路拓扑结构

Fig.9 Line topology optimized by FCM method considering azimuth angle

4）综合考虑方位角和间距的FCM方法+动态Prim算法

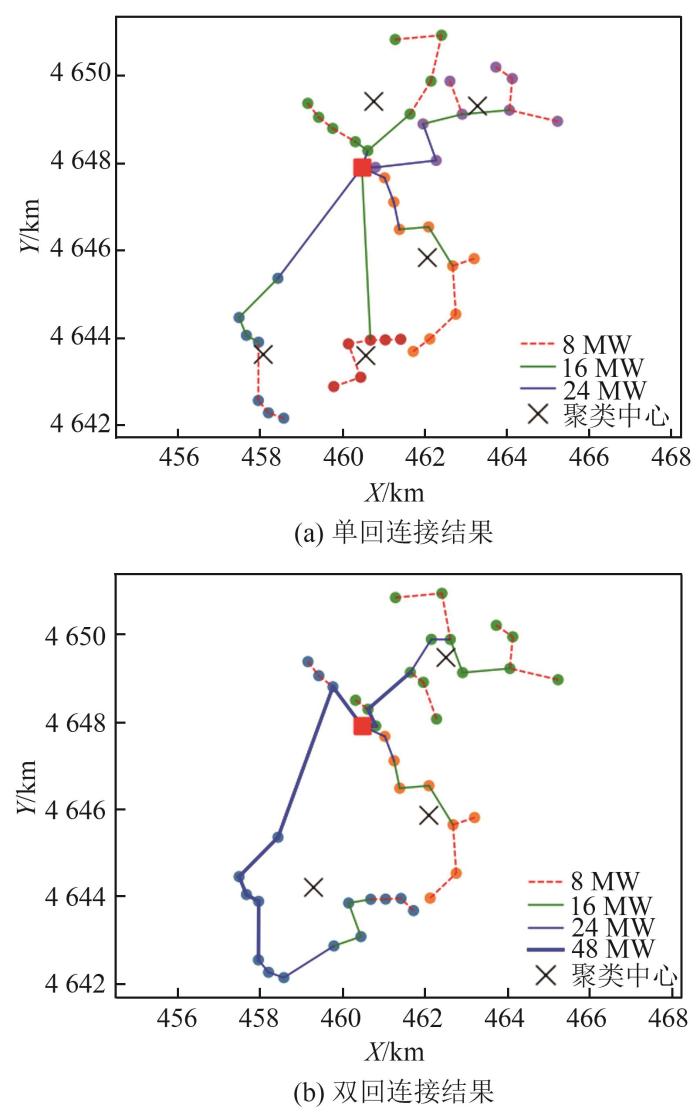
通过计算测试发现，方位角与欧式距离的加权因子k在单回连接取0.98、双回连接取0.89时，线路造价最低。采用该方法优化的集电线路拓扑结构如图10所示，单回、双回连接对应的集电线路系统总造价分别为1 050.86万元和1 061.09万元。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 综合考虑方位角和间距的FCM方法优化的线路拓扑结构

Fig. 10 Line topology optimized by FCM method considering azimuth angle and distance

采用上述4种方法得到的集电线路总造价对比如表2所示。可以看出，使用人工经验设计方法是4种方法中成本最高、效率最低的。使用动态Prim算法得到的双回集电线路系统是4种方法中造价最低的，但该方法在使用单回接线时，存在部分风电机组无法连接到回路的问题。2种先使用FCM方法划分回路再结合动态Prim算法的优化方法，都能保证所有机组接入到回路中，且得到的风电机组数量在各回路中分布较均衡，比较符合工程实际。与只考虑方位角的改进FCM算法相比，考虑方位角和间距的改进FCM算法优化效果更好，单回、双回连接对应的集电线路总造价分别降低了2.6%和5.4%。

表2 不同方法得到的集电线路总造价对比

Tab. 2 Comparison of total cost of collector lines obtained by different methods

方法	单回集电线路总造价/万元	双回集电线路总造价/万元
人工经验设计	—	1 300.00
动态Prim算法	—	1 005.44
考虑方位角的FCM算法+动态Prim算法	1 079.30	1 122.04
综合考虑方位角和间距的FCM算法+动态Prim算法	1 050.86	1 061.09

新窗口打开| 下载CSV

综上可知，在进行集电线路拓扑结构优化时，可以考虑先使用动态Prim算法，在其结果存在“孤立”机组时，再采用考虑方位角和间距的改进FCM算法，并结合动态Prim算法迭代出最优k值。

3 结论

提出了一种基于方位角和欧式距离的改进FCM回路划分方法，结合动态Prim算法对案例风电场进行集电线路拓扑结构优化，并与其他优化方法进行对比，得到如下结论：

1）各种优化算法得到的方案成本都低于人工设计方案，可见使用适当的方法进行集电线路拓扑结构优化，能够有效降低集电线路总造价。

2）在不预先划分回路时，动态Prim算法可能无法生成满足回路容量限制和线路不交叉等约束条件的风电场集电线路方案；如果能产生满足要求的方案，则其总造价在所有对比方案中最低。

3）对于预先划分回路的方案，所提方法兼顾方位角和机组间距，其优化方案总成本比只考虑方位角的方案降低了2.6%~5.4%。

4）所提方法能够给出合理优化的机组回路划分方案，从而降低集电线路总造价，具有一定的工程应用价值。下一步，将围绕回路间容量均衡和k值进一步优化该方法。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

李铮，郭小江，申旭辉，等．

我国海上风电发展关键技术综述

[J]．发电技术，2022，43(2)：186-197． doi:10.12096/j.2096-4528.pgt.22028