高风电渗透率下液流电池储能系统调峰优化控制策略

doi:10.12096/j.2096-4528.pgt.23025

高风电渗透率下液流电池储能系统调峰优化控制策略

李军徽¹, 陈国航¹, 马腾², 李翠萍¹, 朱星旭¹, 贾晨³

1.现代电力系统仿真控制与绿色电能新技术教育部重点实验室(东北电力大学), 吉林省吉林市 132012

2.国网山东省电力公司超高压公司, 山东省济南市 250118

3.国网辽宁省电力有限公司电力科学研究院, 辽宁省沈阳市 110006

Optimal Control Strategy of Peak Shaving of Flow Battery Energy Storage System Under High Wind Power Permeability

LI Junhui¹, CHEN Guohang¹, MA Teng², LI Cuiping¹, ZHU Xingxu¹, JIA Chen³

1.Key Laboratory of Modern Power System Simulation and Control & Renewable Energy Technology, Ministry of Education (Northeast Electric Power University), Jilin 132012, Jilin Province, China

2.State Grid Shandong Electric Extrahigh Voltage Company, Jinan 250118, Shandong Province, China

3.Electric Power Research Institute of State Grid Liaoning Electric Power Co. , Ltd. , Shenyang 110006, Liaoning Province, China

收稿日期: 2023-09-06 修回日期: 2023-12-10

基金资助:

国家电网有限公司科技项目. 5108-202299257A-1-0-ZB

Received: 2023-09-06 Revised: 2023-12-10

作者简介 About authors

李军徽(1976)，男，博士，教授，研究方向为新能源发电联网运行关键技术和储能技术的应用，lijunhui@neepu.edu.cn；

陈国航(1994)，男，硕士研究生，研究方向为储能技术在新能源发电中的应用，guohangchen163@163.com。

摘要

目的在“双碳”目标背景下，解决高风电渗透率系统建设带来的调峰安全性和经济性问题。方法采用电池储能系统削峰填谷的解决方案，提出了一种兼顾技术及经济性的锌溴液流电池(zinc-bromine flow battery，ZBB)储能的调峰优化控制方法。根据实际电池装置，对ZBB储能进行结构解析及数学模型构建。考虑调峰技术性效果，以调峰后的负荷曲线标准差最小为目标函数，提出一种考虑调峰效果的储能双向寻优控制策略。在此基础上，依据电网分时(time of use，TOU)电价政策，以技术性及经济性最优为目标函数，提出一种基于TOU电价机制的储能调峰经济模型，得出储能优化功率时序结果。最后，以东北某地区负荷及风电数据为例，对比验证所提策略的有效性。结果所提策略相较于原负荷，在日均负荷峰谷差、峰谷差率指标上分别降低了35.973%和34.205%，在调峰经济性优化方面提高了5.582%，且合并缓解了电网弃风消纳问题。结论所提策略在达到一定调峰效果的同时，在其全寿命周期内仍保持较好的调峰经济性。

关键词： 储能 ; 风电 ; 液流电池 ; 调峰 ; 双向寻优 ; 优化控制

Abstract

Objectives Under the background of the “dual carbon” target, the safety and economic problems of peak shaving caused by the construction of high wind power penetration system are urgent to be solved. Methods By using the solution of peak shaving and valley filling of battery energy storage system, a peak shaving optimization control method for zinc-bromine flow battery (ZBB) energy storage taking into account both technology and economy was proposed. According to the actual battery device, the structure analysis and the mathematical model construction of ZBB energy storage were carried out. Considering the technical effects of peak shaving, and taking the minimum standard deviation of load curve after peak shaving as the objective function, a bidirectional optimization control strategy for energy storage considering peak shaving effects was proposed. On this basis, according to the time of use (TOU) policy of the power grid, taking the technical and economic optimization as the objective function, an economic model of energy storage peak shaving based on the TOU price mechanism was proposed, and the optimal power timing results for energy storage were obtained. Finally, taking the load and wind power data of a certain area in Northeast China as an example, the effectiveness of the proposed strategy was verified by comparison. Results Compared with the original load, the proposed strategy reduces the daily average load peak-valley difference and peak-valley difference rate by 35.973% and 34.205%, respectively, and improves the peak shaving economic optimization by 5.582%. In addition, the problem of wind curtailment in the power grid is alleviated. Conclusions The proposed strategy achieves a certain peak shaving effect while maintaining a good peak shaving economy throughout its life cycle.

Keywords： energy storage ; wind power ; flow battery ; peak shaving ; bidirectional optimization ; optimal control

PDF (3305KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

李军徽, 陈国航, 马腾, 李翠萍, 朱星旭, 贾晨. 高风电渗透率下液流电池储能系统调峰优化控制策略. 发电技术[J], 2024, 45(3): 434-447 DOI:10.12096/j.2096-4528.pgt.23025

LI Junhui, CHEN Guohang, MA Teng, LI Cuiping, ZHU Xingxu, JIA Chen. Optimal Control Strategy of Peak Shaving of Flow Battery Energy Storage System Under High Wind Power Permeability. Power Generation Technology[J], 2024, 45(3): 434-447 DOI:10.12096/j.2096-4528.pgt.23025

0 引言

为应对能源危机和响应“双碳”目标，以风电为代表的可再生能源发展迅速^[1-2]，截至2022年10月底，风电装机容量约3.5亿kW，同比增长16.6%，占全国累计发电装机容量的14.0%^[3]。由于风电自身具有随机性、波动性及间歇性的特点，高比例风电并网势必给系统源荷供需平衡及安全稳定运行带来调峰等一系列问题^[4-6]。而利用电池储能系统(battery energy storage system，BESS)可以实现电能的时空平移，且具有综合效率高、设置灵活等优势^[7-9]。目前，国内外已建有多项调峰电站示范工程，很多学者对BESS在电网调峰的应用进行了深入研究^[10]。如何制定BESS调峰控制策略，使其达到经济平衡点，并在其全寿命周期内获取最大效益的同时实现良好的调峰效果，是当前研究的主要问题之一。

针对风电并网所带来的电网调峰问题，一些学者针对锂离子电池参与电网调峰的控制策略进行了研究。文献[11]在新能源规模化并网和电网调峰压力日益加剧的背景下，对锂离子电池储能进行了经济性分析，认为其可作为促进新能源消纳和降低电网峰谷差的重要调节资源。文献[12]采用磷酸铁锂BESS，在系统优化调度中嵌入储能模型，求解得到储能最优运行方式和各电源出力。可见，随着近年来锂离子电池的技术突破和价格下降，其商业化发展与技术应用研究逐渐受到关注，但随之而来的储能事故(如北京4·16储能电站事故)引起的相关政策调整，也对锂离子电池储能的大规模应用带来了巨大挑战^[13]。

相比之下，液流电池储能具有更高的安全性、较长时间大容量充放电的储能特性及长循环寿命，面对未来高风电渗透率下巨大的调峰需求，其在储能市场中占有重要地位，尤其是发展较为成熟的全钒液流电池。但全钒液流电池目前受制于高额的钒价格和较高的运维成本，并且其在能量转换效率、能量密度和工作温度等方面仍存在不足^[14]。然而作为同样具有规模化优势的锌溴液流电池(zinc-bromine flow battery，ZBB)技术，与全钒液流电池相比，具有更高的能量密度、安全稳定性、绿色环保性，以及更低的材料成本，其在未来发展前景上更适用于调峰辅助场景的条件需求^[15-17]。

一些学者针对参与调峰的ZBB储能建模及控制策略进行了研究。在电池储能建模方面，文献[18-19]通过数学模型来预测电池反应特性、电流分布，以计算各种充放电条件下的电流、电压和能量效率。文献[20]则更直观地考虑电堆、储液罐等不同部件的特性，并进行数学建模分析。但对于侧重于长时间、大容量运行环境的调峰场景下的ZBB数学模型，在电池组成结构特性、放电深度(depth of discharge，DOD)、循环寿命等模型重要参数方面还有待完善。

在电池储能调峰控制策略方面，文献[21]以负荷曲线方差最小为目标函数，引入储能循环次数和放电深度限制等约束条件，提出一种实时修正调峰控制策略。文献[22-23]以削峰填谷效果最好为目标，提出一种储能调峰变功率控制策略，可有效缓解电网峰谷差过大的问题。文献[24]基于典型日负荷曲线，以经济价值最大为目标函数，考虑储能投资成本、运维成本、环境效益等经济性因素，提出一种电池储能调峰控制策略和配置方案。

然而，上述研究均单独以调峰技术效果或储能经济性为目标，从实际运行及研究价值来看，综合统筹技术及经济性具有重要意义。文献[25]针对兆瓦级电池储能，建立恒功率削峰填谷充放电优化策略，以经济与技术目标函数实时切换的模式运行，但在储能全寿命时间尺度下计算量较大。文献[26-27]综合考虑储能调峰技术及经济性指标，提出兼顾两者的组合调峰优化策略，具有重要借鉴意义，但对于技术性方面的储能电量均衡处理、经济性方面的分时(time of use，TOU)电价主导因素分析及其优化措施还有待完善。

为此，本文从储能参与调峰的技术及经济性角度出发，在设计储能动作策略时，考虑储能系统容量、功率、充放电均衡等约束，以储能经济性最优为目标，求取不同时段充放电量，在此基础上，以调峰效果和经济性综合最优为目标，设计储能系统不同时段充放电功率，进而确定储能系统的控制策略。最后，以东北某地区实际数据为例，对所提方法的有效性进行验证。

1 风电并网对电网调峰需求的影响

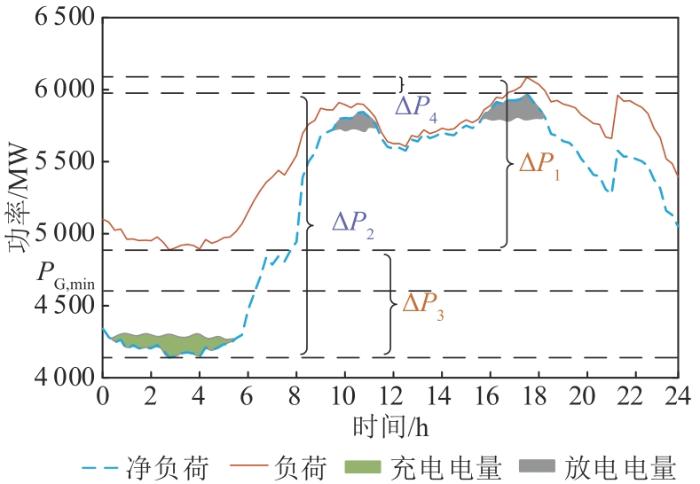
在电力系统中，负荷具有明显的峰谷波动，而调峰的核心就是需要根据负荷需求调节电源出力，保证系统在任何时刻下的源荷供需平衡关系，而风电出力大概率呈现反调峰特性，其大规模并网将会加重调峰负担。为了与传统火电等可控电源进行区分，根据风电历史数据所代表的风力发电能力，将风电作为负的电源，与负荷曲线叠加，即可得风电接入后的电网“净负荷”。

图1分析了典型日风电反调峰对电网调峰需求的影响，其中：ΔP₁=1 198.4 MW，为负荷峰谷差值；ΔP₂=1 833.4 MW，为净负荷峰谷差值；ΔP₃=746.97 MW，为负荷谷值与净负荷谷值之差；ΔP₄=111.99 MW，为负荷峰值与净负荷峰值之差。可以看出，净负荷峰谷差值比负荷峰谷差值高出52.98%，而净负荷谷值比负荷谷值低746.97 MW。因此，高比例风电并网严重增加了调峰机组压力，而这一压力主要体现在负荷低谷时段。为满足向下调峰需求，火电机组必须要降低出力，当超出系统调节能力 $P_{G, m i n}$ 时，系统的源荷供需不再平衡，为保证系统安全稳定运行，被迫采取“弃风限电”的措施，但会导致风资源的大量浪费。而采用布置在电网侧的BESS，发挥其双向调节作用，即在低谷负荷时作为负荷充电，在高峰负荷时作为电源放电，可以实现提高系统调峰能力和风电消纳水平的目的。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 风电反调峰对电网调峰需求的影响

Fig. 1 Impact of wind power reverse peak shaving on peak shaving demand of power grid

2 BESS结构解析及模型构建

2.1 ZBB简析

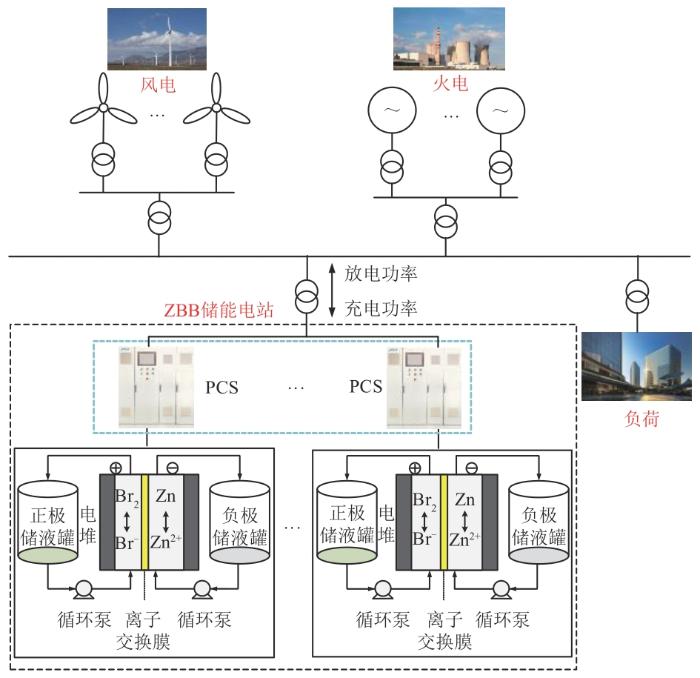
由于ZBB模型对储能经济性分析影响较大，因此需对其内部结构进行分析。图2为ZBB储能系统在电网中的结构，通过调度中心的控制，可以使系统实现调峰作用。ZBB储能系统在建模中可以看作由多个单独运行的电池经过并联组成的电池组，通过功率转换系统(power conversion system，PCS)与电网连接起来。ZBB储能系统结构较为复杂，主要由电堆、储液罐、PCS、循环泵等部分构成。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 ZBB储能系统在电网中的结构

Fig. 2 Structure of ZBB energy storage system in power grid

ZBB储能系统将具有不同价态的离子溶液分别作为正极和负极的活性物质，储存在各自的储液罐中。以溴化锌溶液为反应基底，在对电池进行充放电时，电解液通过循环泵的作用，由外部储液罐分别循环流经电池电堆，并在离子交换膜表面发生氧化和还原反应，实现电池充放电。ZBB充放电时的电化学反应表示如下。

负极：

Z n^{2 +} + 2 e^{-} \underset{放电}{\overset{充电}{⇌}} Z n

(1)

正极：

2 B r^{-} \underset{放电}{\overset{充电}{⇌}} B r_{2} + 2 e^{-}

(2)

最终总的电池反应：

Z n^{2 +} + 2 B r^{-} \underset{放电}{\overset{充电}{⇌}} Z n + B r_{2}

(3)

2.2 BESS数学模型构建

参与调峰的BESS数学模型主要包括储能能量转换效率模型、功率-容量模型、荷电状态(state of charge，SOC)模型以及考虑全寿命周期的模型修正部分。

2.2.1 储能能量转换效率模型

充放电过程中，ZBB的主要损耗包括散热系统所需的风扇供电、控制电解液流向的阀门供电、维持电解液循环的循环泵供电及电堆内反应过程中损失的电量。本文假定每个ZBB储能单元各具有一套散热风扇、电磁阀、循环泵与电堆。

风扇供电损失电量表示为

E_{F} = \sum_{n = 1}^{N} \int_{t_{0}}^{t_{e}} P_{n} d t

(4)

式中： $t_{0}$ 为风扇启动时间； $t_{e}$ 为风扇停止时间； $P_{n}$ 为n号风机的额定功率；N为电池组数。

电磁阀与循环泵损失电量表示为

E_{V} = \sum_{n = 1}^{N} \int_{t_{s}}^{t_{f}} (P_{s} + P_{p}) d t

(5)

式中： $t_{s}$ 为ZBB启动时间； $t_{f}$ 为ZBB关闭时间； $P_{s}$ 为电磁阀额定功率； $P_{p}$ 为循环泵额定功率。

充、放电时的电堆反应损失电量分别表示如下：

\{\begin{array}{l} E_{R c} = η_{c} \sum_{n = 1}^{N} \int_{t_{s}}^{t_{f}} P_{c} d t \\ E_{R d} = η_{d} \sum_{n = 1}^{N} \int_{t_{s}}^{t_{f}} P_{d} d t \end{array}

(6)

式中：η_c、η_d分别为充、放电时的电堆损电率；P_c、P_d分别为充、放电时的电堆实际功率。

综上，针对储能充电后因自放电而引起存储期间电量减小的问题，引入自放电率系数 $r_{d}$ 进行修正，得到BESS的充、放电效率：

\{\begin{array}{l} η_{e, i} = {1 - [(E_{F} + E_{V} + E_{R c}) / E_{r a t e} + r_{d}]} \times 100 % \\ η_{e, o} = [1 - (E_{F} + E_{V} + E_{R d}) / E_{r a t e}] \times 100 % \end{array}

(7)

式中 $E_{r a t e}$ 为BESS的额定容量。

2.2.2 储能功率-容量模型

受PCS限制，BESS充放电功率约束如下：

0 \leq s_{e} (t) P_{B E S S} (t) \leq P_{r a t e}

(8)

s_{e} (t) = \{\begin{array}{l} 1, P_{B E S S} (t) \geq 0 \\ - 1, P_{B E S S} (t) < 0 \end{array}

(9)

式中： $P_{B E S S} (t)$ 为BESS的充放电功率； $P_{r a t e}$ 为BESS额定充放电功率； $s_{e} (t)$ 为充放电标志位，充电时 $s_{e} (t) = 1$ ，放电时 $s_{e} (t) = - 1$ 。

根据BESS充放电功率，可以确定在t到t+1时段内BESS的电量变化情况：

E_{e} (t + 1) = \{\begin{array}{l} E_{e} (t) + \int_{t}^{t + 1} s_{e} (t) P_{B E S S} (t) η_{e, i} d t, P_{B E S S} (t) \geq 0 \\ E_{e} (t) - \int_{t}^{t + 1} s_{e} (t) P_{B E S S} (t) / η_{e, o} d t, P_{B E S S} (t) < 0 \end{array}

(10)

式中 $E_{e} (t)$ 、 $E_{e} (t + 1)$ 分别为BESS在t、t+1时段的电量。

2.2.3 储能SOC模型

在一日T时段内，BESS的截止SOC表示为

S_{O C, e} (t) = S_{O C, s} (t) + \sum_{t = 1}^{T} \frac{E_{e} (t)}{E_{r a t e}}

(11)

式中 $S_{O C, s} (t)$ 为当日BESS的起始SOC。

2.2.4 基于全寿命周期的模型修正

结合现有研究对ZBB不断进行充放电循环实验，得出放电深度 $d_{D}$ 及循环次数/寿命 $N_{c y c}$ 的关系：

N_{c y c} = λ_{0} + λ_{1} d_{D} + λ_{2} d_{D}^{3} + λ_{3} d_{D}^{5}

(12)

式中 $λ_{0}$ 、 $λ_{1}$ 、 $λ_{2}$ 和 $λ_{3}$ 为拟合系数。

对于电解液离子相互转化实现电能储存和释放的液流电池，考虑运行过程中的副反应、离子迁移互串及电池内阻变化等影响因素，对储能 $E_{r a t e}$ 和 $η_{e, i}$ 、 $η_{e, o}$ 进行如下修正：

\{\begin{matrix} E_{r a t e}^{'} = γ \times \sum_{k = 1}^{K} \frac{1}{N_{c y c} (k)} \times E_{r a t e} \\ η_{e, i}^{'} = (1 - \frac{ω}{E_{r a t e}^{'}}) \times η_{e, i} \\ η_{e, o}^{'} = (1 - \frac{ω}{E_{r a t e}^{'}}) \times η_{e, o} \end{matrix}

(13)

式中： $E_{r a t e}^{'}$ 、 $η_{e, i}^{'}$ 和 $η_{e, o}^{'}$ 分别为储能额定容量、充电效率和放电效率修正后的量； $γ$ 、 $ω$ 分别为储能容量、效率修正系数； $N_{c y c} (k)$ 为第k次循环充放电时的储能剩余循环次数；K为总循环次数。

3 高风电渗透率下储能调峰优化控制策略

3.1 考虑调峰效果的BESS双向寻优控制策略

对于已经确定的预测负荷曲线，首先寻找其谷值 $P_{l o a d, m i n}$ 及峰值 $P_{l o a d, m a x}$ ，以其为基准，分别建立填谷功率/电量匹配模型、削峰功率/电量匹配模型和功率/电量均衡调度模型。

1）填谷功率/电量匹配模型

从负荷功率谷值 $P_{l o a d, m i n}$ 开始，以迭代步长 $Δ P$ 向已知负荷功率平均值方向迭代，寻求BESS工作区间，形成上端填谷功率线 $L_{1} = P_{l o a d, m i n} + n_{1} Δ P$ ，与已知预测负荷曲线相交于两点，即( $t_{i}$ _{, $P_{l o a d, m i n} + n_{1} Δ P$ )与( $t_{j}$ _{, $P_{l o a d, m i n} + n_{1} Δ P$ )，求取此时BESS填谷匹配功率 $P_{c}^{m} (t)$ 、填谷匹配电量 $E_{c}^{m} (t)$ 及填谷动作时间区间[ $t_{i}$ _{, $t_{j}$ ]，若不满足式(14)所示约束条件，则继续以步长 $Δ P$ 向上迭代，直至满足约束条件。填谷功率/电量匹配模型以填谷后的负荷曲线标准差最小值 $Δ f_{g}$ 为目标函数，尽可能产生更大的填谷接纳空间，如式(15)所示。}}}

s . t . \{\begin{array}{l} 0 \leq P_{c}^{m} (t) \leq P_{r a t e} \\ 0 \leq P_{d}^{m} (t) \leq P_{r a t e} \\ 0 \leq E_{d}^{m} (t) \leq E_{c}^{m} (t) < E_{r a t e} \\ S_{O C, m i n} \leq S_{O C, e} (t) \leq S_{O C, m a x} \end{array}

(14)

\{\begin{matrix} m i n Δ f_{g} = m i n {\int_{t_{i}}^{t_{j}} [P_{l o a d}^{'} (t) - P_{l o a d, a v g}^{'} {(t)]}^{2} d t / T_{1}}^{1 / 2} \\ P_{c}^{m} (t) = (P_{l o a d, m i n} + n_{1} Δ P) - P_{l o a d} (t) \\ P_{l o a d}^{'} (t) = P_{l o a d} (t) + P_{c}^{m} (t) \\ E_{c}^{m} (t) = \int_{t_{i}}^{t_{j}} P_{c}^{m} (t) η_{e, i} d t \end{matrix}

(15)

式中： $P_{d}^{m} (t)$ 为BESS削峰匹配功率； $E_{d}^{m} (t)$ 为BESS削峰匹配电量； $S_{O C, m a x}$ 、 $S_{O C, m i n}$ 分别为BESS荷电状态上、下限值； $P_{l o a d} (t)$ 为负荷功率； $P_{l o a d}^{'} (t)$ 为储能填谷后的负荷功率； $P_{l o a d, a v g}^{'} (t)$ 为储能填谷后的负荷功率平均值； $T_{1}$ 为填谷动作时段； $n_{1}$ 为填谷迭代次数。

2）削峰功率/电量匹配模型

从负荷功率峰值 $P_{l o a d, m a x}$ 开始，以迭代步长 $Δ P$ 向已知负荷功率平均值方向进行迭代，形成下端削峰功率线 $L_{2} = P_{l o a d, m a x} - n_{2} Δ P$ ，与已知预测负荷曲线相交于两点，即( $t_{i}^{'}$ _{, $P_{l o a d, m a x} - n_{2} Δ P$ )与( $t_{j}^{'}$ _{, $P_{l o a d, m a x} - n_{2} Δ P$ )，求取 $P_{d}^{m} (t)$ 、 $E_{d}^{m} (t)$ 以及削峰动作时间区间[ $t_{i}^{'}$ _{, $t_{j}^{'}$ ]，若不满足式(14)所示约束条件，则继续以步长 $Δ P$ 向下迭代，直至满足约束条件。削峰功率/电量匹配模型以削峰后的负荷曲线标准差最小值 $Δ f_{f}$ 为目标函数，尽可能产生更大的削峰释放空间，如式(16)所示。}}}

\{\begin{matrix} m i n Δ f_{f} = m i n {\int_{t_{i}^{'}}^{t_{j}^{'}} [P_{l o a d}^{″} (t) - P_{l o a d, a v g}^{″} {(t)]}^{2} d t / T_{2}}^{1 / 2} \\ P_{d}^{m} (t) = P_{l o a d} (t) - (P_{l o a d, m a x} - n_{2} Δ P) \\ P_{l o a d}^{″} (t) = P_{l o a d} (t) - P_{d}^{m} (t) \\ E_{d}^{m} (t) = \int_{t_{i}^{'}}^{t_{j}^{'}} P_{d}^{m} (t) / η_{e, o} d t \end{matrix}

(16)

式中： $P_{l o a d}^{″} (t)$ 为储能削峰后的负荷功率； $P_{l o a d, a v g}^{″} (t)$ 为储能削峰后的负荷功率平均值； $T_{2}$ 为储能削峰动作时段； $n_{2}$ 为削峰迭代次数。

3）功率/电量均衡调度模型

为保证BESS在削峰和填谷双向寻优过程中的充放电功率/电量平衡，规定在一日内BESS的充放电功率/电量一致。由于填谷、削峰功率/电量匹配模型每经过一次迭代均要得到新的 $P_{c}^{m} (t)$ 、 $E_{c}^{m} (t)$ 及 $P_{d}^{m} (t)$ 、 $E_{d}^{m} (t)$ ，因此针对以上4个迭代结果对应设置4个均衡判断因子 $α_{P_{c}^{m} (t)}$ 、 $β_{E_{c}^{m} (t)}$ 及 $α_{P_{d}^{m} (t)}$ 、 $β_{E_{d}^{m} (t)}$ ，均衡判据 $φ$ 取4个均衡判断因子中的最小值，且只有其小于设定的允许值 $ε$ 时，才运行均衡调度方法，如式(17)、(18)所示。

\{\begin{matrix} α_{P_{c}^{m} (t)} = P_{r a t e} - P_{c}^{m} (t) \\ α_{P_{d}^{m} (t)} = P_{r a t e} - P_{d}^{m} (t) \\ β_{E_{c}^{m} (t)} = E_{r a t e}^{″} - E_{c}^{m} (t) \\ β_{E_{d}^{m} (t)} = E_{r a t e}^{″} - E_{d}^{m} (t) \\ E_{r a t e}^{″} = E_{r a t e} (S_{O C, m a x} - S_{O C, m i n}) \end{matrix}

(17)

φ = m i n {α_{P_{c}^{m} (t)}, α_{P_{d}^{m} (t)}, β_{E_{c}^{m} (t)}, β_{E_{d}^{m} (t)}} < ε

(18)

式中 $E_{r a t e}^{″}$ 为储能容量迭代阈值。

对均衡调度方法进行如下解析：

①当 $φ = α_{P_{c}^{m} (t)}$ 时，表明 $P_{c}^{m} (t)$ 先达到迭代阈值，而此时 $E_{c}^{m} (t)$ 未达到迭代阈值 $E_{r a t e}^{″}$ ，存在未利用容量，因此应调用填谷功率/电量匹配模型，继续增大向上迭代次数 $n_{1}$ ，在约束条件下，得出新的 $P_{c}^{m} (t)$ 及[ $t_{i}$ _{, $t_{j}$ ]，直至 $E_{c}^{m} (t)$ 达到限值时，方可结束填谷模型迭代。此时， $P_{d}^{m} (t)$ 和 $E_{d}^{m} (t)$ 未达到限值，调用削峰功率/电量匹配模型，继续增大向下迭代次数 $n_{2}$ ，得出新的 $P_{d}^{m} (t)$ 及[ $t_{i}^{'}$ _{, $t_{j}^{'}$ ]。若 $P_{d}^{m} (t)$ 先达到限值，则继续增大向下迭代次数 $n_{2}$ ；而若 $E_{d}^{m} (t)$ 先达到限值或两者同时达到限值，则结束削峰模型迭代。}}

②当 $φ = β_{E_{c}^{m} (t)}$ 时，表明 $E_{c}^{m} (t)$ 先达到迭代阈值，结束填谷模型迭代。此时， $P_{d}^{m} (t)$ 和 $E_{d}^{m} (t)$ 未达到限值，之后的处理方法与 $φ = α_{P_{c}^{m} (t)}$ 时相同。

③当 $φ = α_{P_{d}^{m} (t)}$ 时，表明 $P_{d}^{m} (t)$ 先达到迭代阈值，而此时 $E_{d}^{m} (t)$ 未达到迭代阈值 $E_{r a t e}^{″}$ ，存在未利用容量，故应调用削峰功率/电量匹配模型，继续增大向下迭代次数 $n_{2}$ ，在约束条件下，得出新的 $P_{d}^{m} (t)$ 及[ $t_{i}^{'}$ _{, $t_{j}^{'}$ ]，直至 $E_{d}^{m} (t)$ 达到限值时，方可结束削峰模型迭代。此时， $P_{c}^{m} (t)$ 和 $E_{c}^{m} (t)$ 未达到限值，调用填谷功率/电量匹配模型，继续增大向上迭代次数 $n_{1}$ ，得出新的 $P_{c}^{m} (t)$ 及[ $t_{i}$ _{, $t_{j}$ ]。若 $P_{c}^{m} (t)$ 先达到限值，则继续增大向上迭代次数 $n_{1}$ ；而若 $E_{c}^{m} (t)$ 先达到限值或两者同时达到限值，则结束填谷模型迭代。}}

④当 $φ = β_{E_{d}^{m} (t)}$ 时，表明 $E_{d}^{m} (t)$ 先达到迭代阈值，结束削峰模型迭代。此时， $P_{c}^{m} (t)$ 和 $E_{c}^{m} (t)$ 未达到限值，之后的处理方法与 $φ = α_{P_{d}^{m} (t)}$ 时相同。

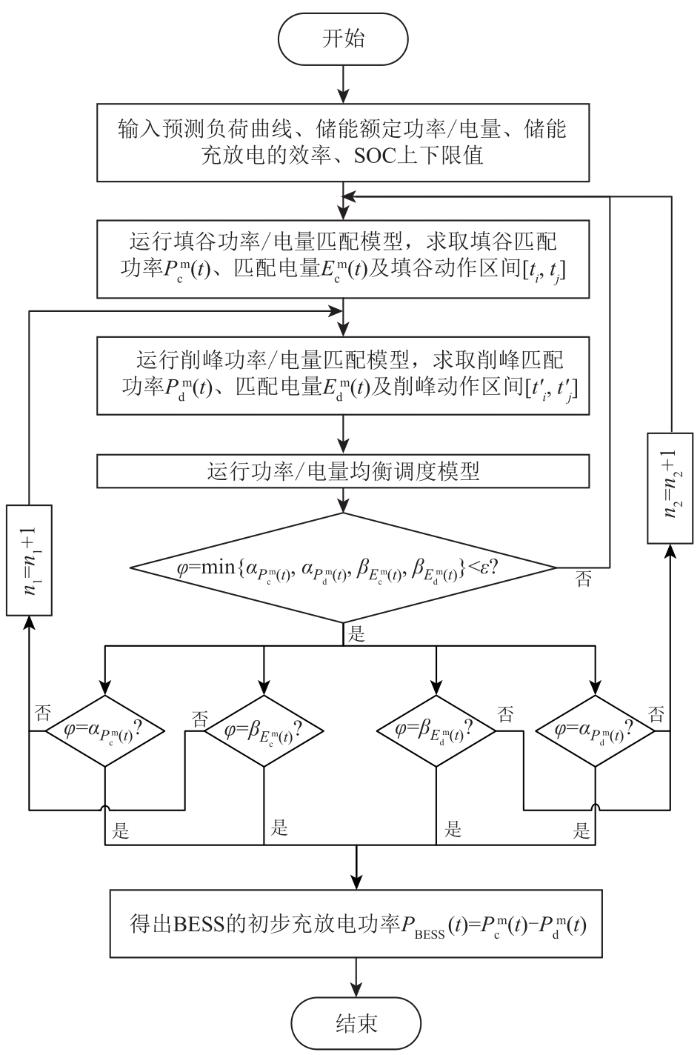
通过填谷功率/电量匹配模型、削峰功率/电量匹配模型及功率/电量均衡调度模型构成的双向寻优控制策略分析，可得出充放电功率 $P_{B E S S} (t)$ 和储能调峰后的负荷功率 $P_{l o a d, t f} (t)$ ，分别如式(19)、(20)所示。BESS的控制策略流程如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 考虑调峰效果的BESS双向寻优控制策略流程图Fig. 3 Flow chart of BESS bidirectional optimization control strategy considering peak shaving effect

P_{B E S S} (t) = P_{c}^{m} (t) - P_{d}^{m} (t)

(19)

P_{l o a d, t f} (t) = P_{l o a d}^{'} (t) + P_{l o a d}^{″} (t)

(20)

3.2 考虑调峰经济性的BESS运行策略

3.2.1 BESS调峰经济评价指标

参与电网调峰的BESS调峰经济评价指标模型构建需考虑收益因素与成本因素，其中：收益因素包括运行收益、补偿收益、环境收益；成本因素包括BESS的建设成本、运行维护成本、废弃回收成本。

1）收益分析

①BESS运行收益

“低储高发”的运行方式获得的收益为BESS运行收益，可表示为

I_{r u n} = \sum_{t = 1}^{T} [P_{d}^{m} (t) P_{p r i c e} (t) - P_{c}^{m} (t) P_{p r i c e} (t)] Δ t

(21)

式中： $I_{r u n}$ 为BESS日运行收益，元； $P_{p r i c e} (t)$ 为t时段峰谷电价，元/(kW⋅h)； $Δ t$ 为数据采样时间步长。

②BESS补偿收益

本文采用调峰电量补偿方法进行补偿，获得的BESS补偿收益表示为

I_{c o m} = \sum_{t = 1}^{T} P_{c o m} [P_{c}^{m} (t) + P_{d}^{m} (t)] Δ t

(22)

式中： $I_{c o m}$ 为BESS日补偿收益，元； $P_{c o m}$ 为单位电量补偿价格，元/(kW⋅h)。

③BESS环境收益

环境收益是指其通过多接纳风电来减少煤炭燃烧获得的节煤效益及减少环境污染获取的社会效益，可表示为

I_{e n v} = \sum_{d = 1}^{D} E_{p m, d} \times (p_{e n} + p_{s c})

(23)

式中： $E_{p m, d}$ 为第d日通过储能系统多接纳的风电量，MW⋅h； $p_{e n}$ 为火电机组产生单位电量所造成的环境污染治理费用，元/(MW⋅h)； $p_{s c}$ 为风电单位节煤效益，元/(MW⋅h)；D为储能系统寿命，d。

在负荷低谷时段，风电接纳量受火电机组出力下限、风电出力情况及BESS电量、功率的影响，表达式如下：

P_{w i n d}^{j n k j} (t) = P_{l o a d} (t) - P_{G, m i n}

(24)

P_{w i n d, b w} (t) = \{\begin{matrix} P_{w i n d}^{j n k j} (t), & P_{w i n d} (t) > P_{w i n d}^{j n k j} (t) \\ P_{w i n d} (t), & P_{w i n d} (t) \leq P_{w i n d}^{j n k j} (t) \end{matrix}

(25)

P_{w i n d}^{B E S S} (t) = P_{l o a d} (t) + P_{B E S S} (t) - P_{G, m i n}

(26)

P_{w i n d, b w}^{B E S S} (t) = \{\begin{matrix} P_{w i n d}^{B E S S} (t), & P_{w i n d} (t) > P_{w i n d}^{B E S S} (t) \\ P_{w i n d} (t), & P_{w i n d} (t) \leq P_{w i n d}^{B E S S} (t) \end{matrix}

(27)

E_{p m} = \sum_{t = 1}^{T} [P_{w i n d, b w}^{B E S S} (t) - P_{w i n d, b w} (t)] Δ t

(28)

式中： $E_{p m}$ 为通过BESS作用多接纳的风电量； $P_{w i n d}^{j n k j} (t)$ 、 $P_{w i n d, b w} (t)$ 分别为t时段不含储能的风电功率接纳空间和风电并网功率； $P_{w i n d}^{B E S S} (t)$ 、 $P_{w i n d, b w}^{B E S S} (t)$ 分别为t时段含储能的风电功率接纳空间和风电并网功率； $P_{w i n d} (t)$ 为t时段总风电功率。

2）成本分析

①BESS建设成本

建设成本是指BESS建设时的初始一次投资，主要包括电量成本与功率成本，考虑资金的时间价值，对储能建设成本进行修正，可表示为

C_{C I} = (E_{r a t e} \times C_{E} + P_{r a t e} \times C_{P}) \times \frac{r {(1 + r)}^{y}}{{(1 + r)}^{y} - 1}

(29)

式中： $C_{E}$ 为储能电量成本单价，元/(kW⋅h)； $C_{P}$ 为储能功率成本单价，元/kW； $r$ 为基准折现率； $y$ 为储能系统寿命年限，a。

②BESS运行维护成本

运行维护成本是指BESS在寿命期内充放电运行的过程中，因进行维护检修、更换损坏及老化零件等产生的费用，主要与充放电次数、深度有关，可表示为

C_{R M} = \sum_{t = 1}^{T} C_{M} [P_{c}^{m} (t) + P_{d}^{m} (t)] Δ t

(30)

式中： $C_{R M}$ 为BESS日运行维护成本： $C_{M}$ 为单位运维成本，元/(kW⋅h)。

③BESS废弃回收成本

废弃回收成本是指BESS在其寿命终结后无污染处理电池的费用与回收电池中的可利用金属价格之差，可表示为

C_{R E} = \sum_{i = 1}^{m} (p_{h} - p_{m, i} α_{m, i}) θ_{b e s s} E_{r a t e}

(31)

式中： $m$ 为BESS中金属种类总数； $p_{h}$ 为废弃BESS所需费用，元/t； $p_{m, i}$ 为BESS中金属 $i$ 的单价，元/t； $α_{m, i}$ 为BESS中金属 $i$ 的质量，t； $θ_{b e s s}$ 为BESS能重比，t/(MW⋅h)。

3.2.2 基于TOU电价机制的BESS调峰经济模型

鉴于不同时段的电价差异，需要考虑不同时段电价及BESS的SOC状态来设置其运行策略。环境收益主要是由BESS多接纳的风电量来决定，运行收益主要是由峰时段放电量来决定，而补偿收益主要受负荷谷时段火电机组出力达下限后其充电量的影响。根据当前研究及政策导向，储能的运营模式及收益组成主要与峰谷平的分时电价机制有关。在明确储能调峰收益的主要影响因素基础上，根据东北某区域电网2021年的分时电价政策，将一天24 h划分为3个平值时段、2个峰值时段与1个谷值时段，如表1所示。

表1 负荷峰平谷时段划分标准

Tab. 1 Time division criteria for peak load, flat load and valley load

峰值时段	谷值时段	平值时段
T_p，1：09:00—12:00	T_v，1：23:00—06:00	T_f，1：06:00—09:00
T_p，2：17:00—21:00	—	T_f，2：12:00—17:00
—	—	T_f，3：21:00—23:00

新窗口打开| 下载CSV

为兼顾调峰经济性与技术性指标，以调峰后负荷标准差改善量及储能净收益标幺值之和最大为总优化目标函数，进行经济性时段优化匹配。

调峰后负荷标准差改善量 $S_{D}$ 为原负荷标准差 $S_{D_{1}}$ 与储能调峰后负荷标准差 $S_{D_{2}}$ 之差，表示如下：

S_{D_{1}} = \sqrt[]{\sum_{t = 1}^{T} [P_{l o a d} (t) - P_{l o a d, a v g} {(t)]}^{2} / T}

(32)

S_{D_{2}} = \sqrt[]{\sum_{t = 1}^{T} [P_{l o a d, t f} (t) - P_{l o a d, t f, a v g} {(t)]}^{2} / T}

(33)

S_{D} = S_{D_{1}} - S_{D_{2}}

(34)

式中： $P_{l o a d, a v g} (t)$ 为原负荷功率平均值； $P_{l o a d, t f} (t)$ 为储能调峰后的负荷功率； $P_{l o a d, t f, a v g} (t)$ 为储能调峰后的负荷功率平均值。

结合储能调峰经济评价指标模型，储能调峰净收益 $I_{I}$ 为各收益组成与各成本组成之差，即

I_{I} = I_{e n v} + I_{r u n} + I_{c o m} - C_{C I} - C_{R M} - C_{R E}

(35)

对调峰后负荷标准差改善量及储能净收益进行如下标幺化处理：

{S_{D}}^{*} = S_{D} / S_{D_{1}}

(36)

{I_{I}}^{*} = I_{I} / (I_{e n v} + I_{r u n} + I_{c o m})

(37)

最终形成总优化目标函数 $F$ ：

m a x F = {I_{I}}^{*} + {S_{D}}^{*}

(38)

结合以上分析，按照表1中峰值、平值、谷值时段，对考虑调峰效果的储能双向寻优控制策略时序结果进行划分，导入基于TOU电价机制的BESS调峰经济模型中进行优化计算，此模型包含以下3个部分。

1）谷值充电功率分配模型

谷值充电功率主要与环境收益、补偿收益有关，因此希望储能尽量在谷值电价时段充电，峰值电价时段坚决不充电，平值电价时段适当充电。依据此分配原则，若充电功率均发生在T_v,1时段，表明充电成本最小，模型不动作；若不满足，则调用双向寻优策略的填谷模型削减T_f,1、T_f,2和T_f,3范围内的充电功率，并同时增加T_v,1时段的充电功率，以建立新的匹配时段，若此时缓解弃风问题，则优先匹配选择，以增加环境收益，否则保留平值范围动作时段。

2）平值充放电功率分配模型

平值充放电功率与环境收益、运行收益、补偿收益呈弱相关，因此其作为中间枢纽，调用双向寻优策略的均衡模型，将来自谷值和峰值的充/放电时序功率存放到T_f,1、T_f,2和T_f,3时段。

3）峰值放电功率分配模型

峰值放电功率主要与运行收益有关，因此希望储能尽量在峰值电价时段放电，在谷值电价时段坚决不放电，在平值电价时段适当放电。因此，如果放电功率均发生在T_p,1和T_p,2时段，表明放电收益最大，模型不动作；如果不满足，则调用双向寻优策略的削峰模型削减T_f,1、T_f,2和T_f,3范围内的放电功率，并同时增加T_p,1和T_p,2时段的放电功率，以建立新的匹配时段，若此时满足削减弃风条件，则优先匹配选择，否则保留平值范围动作时段。

3.3 评价指标

兼顾调峰技术经济性的控制策略评价指标主要由负荷峰谷差、负荷峰谷差率、弃风电量以及储能系统净收益率4个指标组成。

1）负荷峰谷差

负荷峰谷差 $α$ 定义为系统在一个调度日内的最大负荷与最小负荷之差，其表达式为

α = P_{l o a d, m a x} - P_{l o a d, m i n}

(39)

2）负荷峰谷差率

负荷峰谷差率 $β$ 定义为系统在一个调度日内的峰谷差与最大负荷的比值，其表达式为

β = \frac{P_{l o a d, m a x} - P_{l o a d, m i n}}{P_{l o a d, m a x}} \times 100 %

(40)

3）弃风电量

当某一时段的风电功率超出储能系统及火电机组提供的风电接纳空间时，就会有弃风产生，弃风电量 $E_{w i n d, q f}$ 的表达式如下：

E_{w i n d, q f} = \sum_{t = 1}^{T} P_{w i n d, q f} (t)

(41)

P_{w i n d, q f} (t) = P_{w i n d} (t) - P_{w i n d, b w}^{B E S S} (t)

(42)

式中 $P_{w i n d, q f} (t)$ 为t时段的弃风功率。

4）储能系统净收益率

储能系统净收益率 $I$ 定义为储能系统在其全寿命周期内，通过参与调峰辅助服务获得的净收益 $I_{I}$ 与总成本之比，用于衡量不同成本储能的运营收益情况，其表达式为

I = \frac{I_{I}}{C_{C I} + C_{R M} + C_{R E}} \times 100 %

(43)

4 算例分析

4.1 算例参数

1）BESS计算参数设置

本算例储能系统应用于发电侧，采用集中式ZBB以大规模应用于调峰场景，储能配置采用目前规模最大的200 MW/800 MW⋅h液流电池，储能初始电量为80 MW⋅h。表2为BESS计算参数。

表2 BESS计算参数

Tab. 2 BESS calculation parameters

参数	数值
循环次数(100% DOD)	14 000
$p_{e n}$ /[元/(MW⋅h)]	230
$p_{s c}$ /[元/(MW⋅h)]	205
$C_{E}$ /[元/(kW⋅h)]	5 000
$C_{P}$ /(元/kW)	2 000
$C_{M}$ /[元/(kW⋅h)]	0.1
$p_{m, i}$ /(万元/t)	1.6
$α_{m, i}$ /t	0.15
$p_{h}$ /(万元/t)	3.5
$θ_{b e s s}$ /[t/(MW⋅h)]	33

新窗口打开| 下载CSV

储能调峰补偿价格按照东北电力辅助市场规则设置单价 $P_{c o m}$ =0.7元/(kW⋅h)；储能SOC上、下限值分别为 $S_{O C, m a x}$ =0.9， $S_{O C, m i n}$ =0.1；基准折现率 $r$ =6%。本文假定储能采用单日一充一放工作制，由表2可知储能寿命D为14 000 d。

2）火电机组计算参数设置

火电机组装机容量为8 700 MW，由于本文主要针对参与调峰的储能系统全寿命周期的技术性及经济性进行分析，故假定火电机组可通过常规调峰(最小技术出力50%)、深度调峰(最小技术出力30%)满足系统负荷供需平衡。

3）仿真分析数据

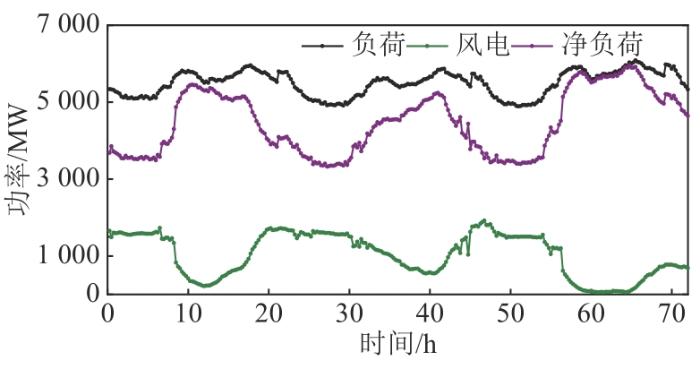
以东北某地区一个月风电及负荷数据为例进行分析，数据采样时间间隔为15 min，风电装机容量为2 000 MW，负荷峰、谷值分别为6 441.5、3 706.8 MW，并采用风电出力测算方法构建高风电渗透率场景，日风电渗透率为20%~50%，以预测未来高风电渗透率对调峰情况的影响。为便于对比分析结果，选取该地区3日典型风电及负荷数据进行分析，如图4所示，风电渗透率为30%，风电并网单价为0.375元/(kW⋅h)，选取迭代步长 $Δ P$ =0.01 MW。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 3日风电及负荷出力曲线

Fig. 4 Three-day wind power and load output curves

为体现本文所提策略在提高BESS参与电网调峰的技术性和经济性方面的作用，对比分析了3种不同调度策略下的调峰情况：策略1采用BESS在任意时刻均以恒定功率进行削峰填谷的恒功率储能控制策略^[25]；策略2仅以调峰后的负荷曲线标准差最小为目标函数，实现BESS调峰效果最大化，不考虑全寿命周期内储能调峰经济性及运行寿命；策略3为本文所提策略。

4.2 算例结果分析

4.2.1 ZBB数学模型效果分析

在MATLAB仿真软件中搭建全寿命周期ZBB数学模型，结合文献[18-22]中电池模型参数，在储能额定功率运行下，设置整体散热风扇、电磁阀和循环泵均随储能工作时运行，各额定功率分别为 $P_{n}$ =8.0 MW， $P_{s}$ =4.5 MW， $P_{p}$ =7.5 MW，充放电时的电堆损电率η_c=η_d=5%，并考虑0.1%的日自放电率，计算得到储能充、放电效率分别为84.9%、85%。另外，储能工作中的功率、容量及SOC值均可满足模型约束条件。

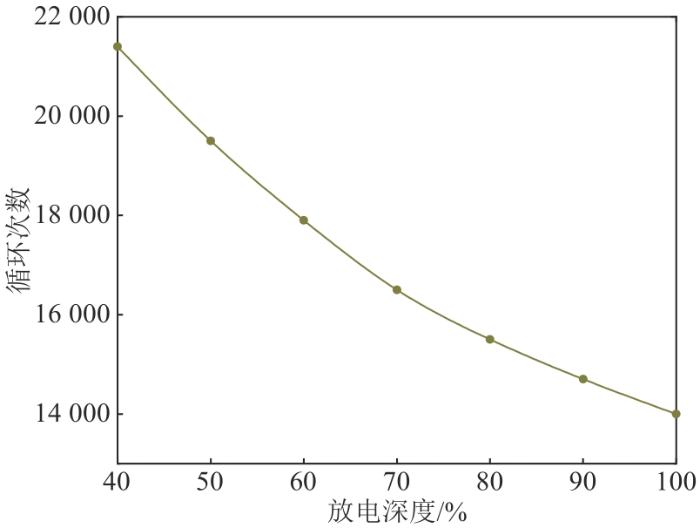
在储能全寿命周期模型推算中，设置循环次数与放电深度的拟合系数分别为 $λ_{0}$ =31 276.596， $λ_{1}$ =-26 585.106， $λ_{2}$ =13 186.809， $λ_{3}$ =-3 878.298，得到ZBB循环次数与放电深度的关系曲线如图5所示。可以看出，随着放电深度增大，储能的循环次数呈非线性下降趋势，证明所建模型有效。考虑储能SOC上下限值，算例采用80%DOD对应的储能循环次数15 500，寿命约为42 a。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 ZBB循环次数与放电深度的关系曲线

Fig. 5 ZBB cycle number and DOD relationship curve

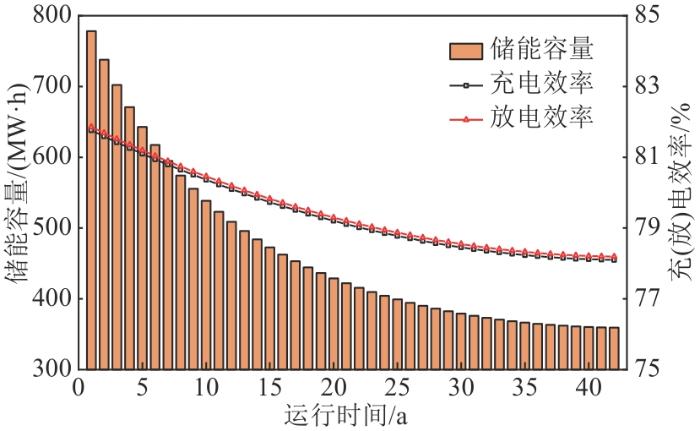
基于上述条件，设定储能容量、效率修正系数分别为 $γ$ =9.897 $\times$ 10⁷， $ω$ =28.775，计算得到ZBB储能容量及效率运行衰减情况，如图6所示。可以看出，随着运行时间的增加，储能容量及效率呈非线性衰减趋势，将不同控制策略下的功率代入此储能衰减模型中，即可推算出全寿命周期调峰情况。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 ZBB储能容量及效率运行衰减情况

Fig. 6 ZBB energy storage capacity and efficiency operating attenuation situation

4.2.2 储能调峰控制策略效果分析

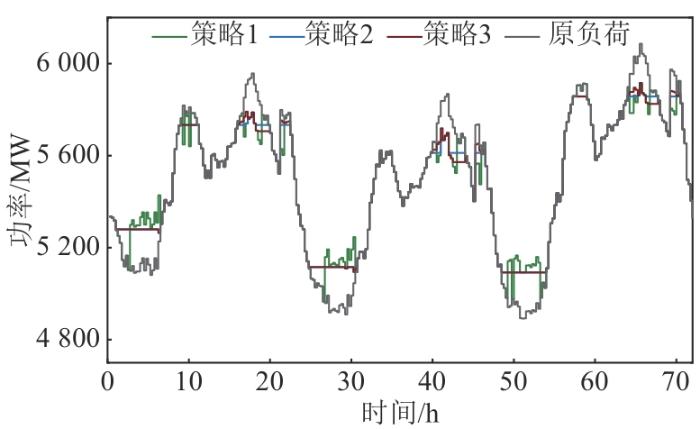
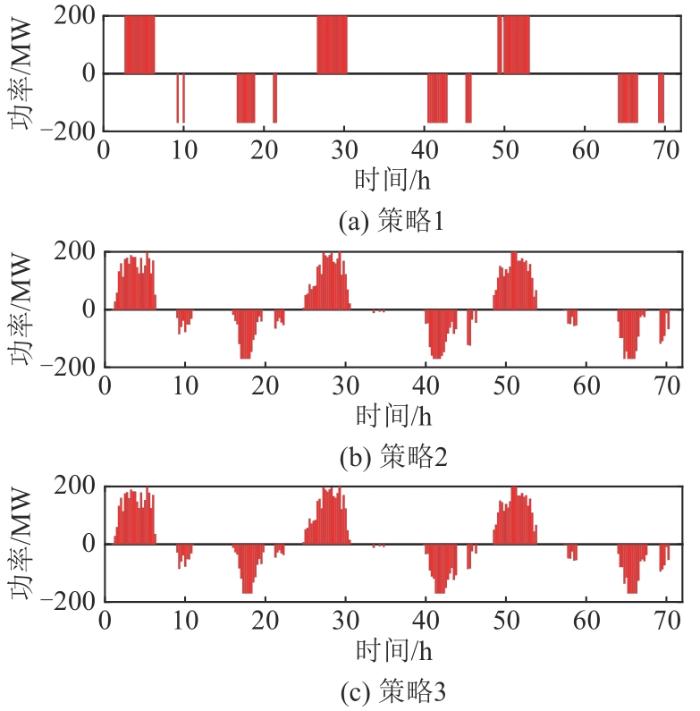
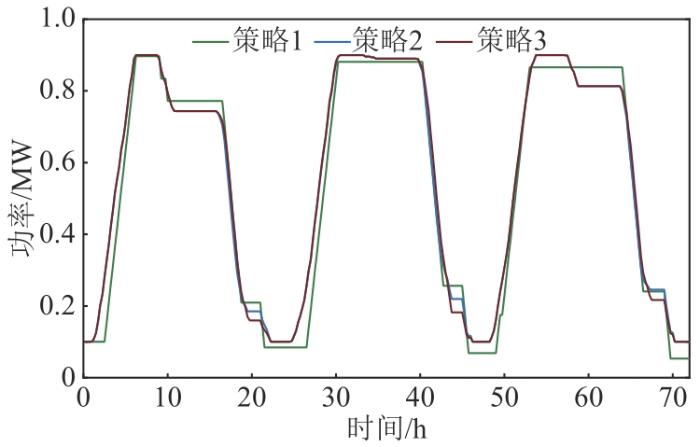
参与调峰的3种不同储能系统控制策略下的负荷曲线、储能充放电功率和储能SOC结果对比分别如图7—9所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 不同策略下储能调峰优化后的负荷曲线

Fig. 7 Load curves after energy storage peak shaving optimization under different strategies

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 不同策略下储能充放电功率对比

Fig. 8 Comparison of energy storage charge and discharge power under different strategies

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 不同策略下储能SOC对比

Fig. 9 Comparison of energy storage SOC under different strategies

由图7可见，策略2、3的调峰效果均明显优于策略1。通过数据分析可知，与原负荷曲线相比，策略1峰谷差改善量为219.958 MW；策略2、3的峰谷差改善量分别为369.228、350.918 MW，分别比策略1提高了67.863%和59.539%。之所以策略1调峰效果较差，是因为其充放电功率的硬性恒定限制条件，导致与迭代得到的允许充放电时段存在不均衡分配，并易受到负荷最值所处时段位置限制，故不能灵活优化负荷曲线。但就全考虑调峰技术性的策略2而言，策略3的峰谷差改善量占其95.041%，因此其在调峰优化后的负荷曲线调峰效果上仍具有一定的优势。

由图8、9可以看出，具有含均衡判断因子的功率/电量均衡调度模型的策略2、3可通过控制削峰及填谷模型的双向迭代，达到均衡寻优的目的，而策略1则对储能充放电的协调处理欠优。图9表明，除初始SOC为定值外，策略1在每日充放电中均出现了最小值SOC越限、最大值SOC未达限的情况，并且失衡问题呈逐日累加趋势，直至第3 日，最小值SOC仅为0.053，严重不满足0.1的约束限值，同时其储能充放电次数也要多于策略2、3，如此发展会对BESS的循环寿命造成影响，损害储能全寿命周期内的调峰经济性。此外，通过对比策略2、3可以看出，经过基于TOU电价机制经济分配的储能充放电策略在日放电末端的曲线较为平缓，因此两者在相同的放电深度下，策略3指导下的储能放电速率较小，储能老化速度较慢，更有利于延长电池寿命。

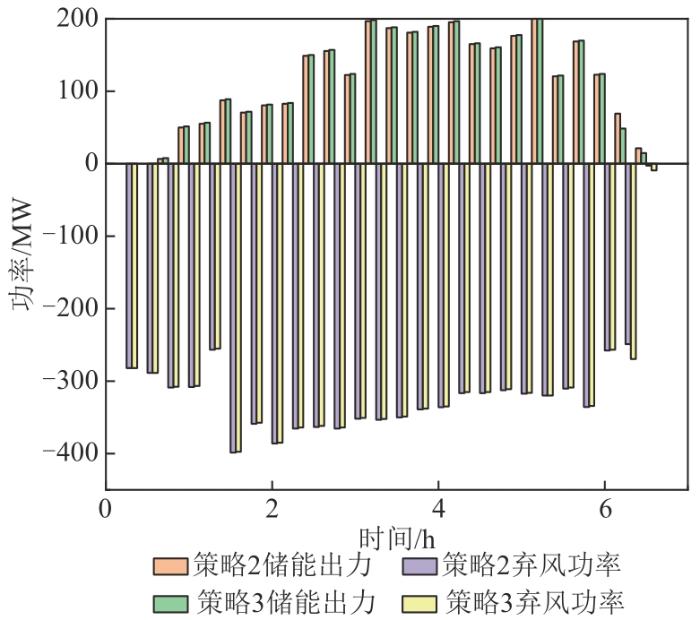
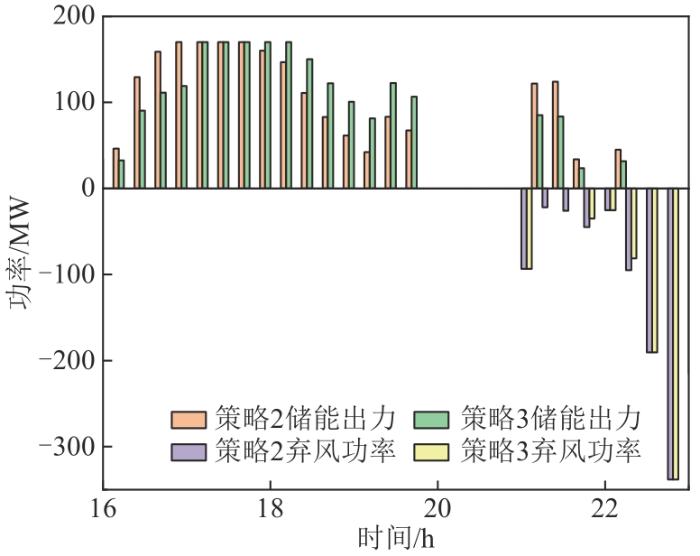
为进一步凸显策略3在调峰经济性方面的贡献，分别对策略2、3下储能削峰填谷时的充放电出力及对应的弃风情况进行对比分析。策略2、3下储能充电与弃风情况如图10所示，可以看出，策略3可通过分时电价区间进行储能功率再分配，在尽量不增加弃风电量的前提下提升储能调峰经济性。策略2、3下储能放电与弃风情况如图11所示，可以看出，相比于策略2，策略3削减了低放电电价时段的储能出力，提高了高放电电价时段的储能功率，在提升调峰经济性的同时增大了风电并网空间，有效缓解甚至消除了弃风问题。数据分析结果显示，仅在第2日策略3比策略2降低了17.775 MW⋅h的弃风电量，提升了0.667万元的风电并网收益，表明策略3在均衡调峰技术及经济性的同时，也有利于提升风电消纳能力。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 策略2、3下储能充电与弃风情况对比

Fig. 10 Comparison of energy storage charging and wind curtailment under strategy 2 or 3

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 策略2、3下储能放电与弃风情况对比

Fig. 11 Comparison of energy storage discharge and wind curtailment under strategy 2 or 3

根据典型日3种策略的分析结果，结合该地区一个月风电及负荷计算数据，并根据储能时序功率及表3所示分时电价，评估储能全寿命周期内的经济性。各控制策略评价指标如表4所示。

表3 分时电价参数

Tab. 3 Time-of-use electricity price parameters

分时电价	单价/[元/(kW⋅h)]	时段
谷值电价	0.414	23:00—06:00
平值电价	0.782	06:00—09:00，12:00—17:00，21:00—23:00
峰值电价	1.149	09:00—12:00，17:00—21:00

新窗口打开| 下载CSV

表4 各控制策略评价指标

Tab. 4 Evaluation indicators of each control strategy

控制策略	日均负荷峰谷差/MW	日均负荷峰谷差率/%	日均负荷标准差改善量/MW	储能净收益率/%	日均弃风电量/(MW⋅h)
无储能调节	972.311	16.287	—	—	6 216.138
策略1	760.814	13.105	69.124	10.445	4 964.578
策略2	603.470	10.397	73.537	10.626	4 942.015
策略3	622.537	10.716	73.164	11.028	4 936.140

新窗口打开| 下载CSV

由表4可见，3种控制策略均提升了调峰效果，相较于原负荷，策略1、2、3的日均负荷峰谷差分别降低了21.752%、37.934%和35.973%，日均负荷峰谷差率分别降低了19.555%、36.164%和34.205%，并且策略2、3在调峰技术性的改善效果上更为明显，这一结论从日均负荷标准差改善量上也能够体现。

在调峰经济性方面，从净收益上来看，策略3控制下的储能净收益率最高，分别较策略1、2提高了5.582%、3.783%。各控制策略下储能收益如表5所示。在运行收益和环境收益方面，策略2较策略1分别提升了2.177%和2.651%，策略3较策略2则分别提升了9.048%和0.673%，这是因为策略3进行了基于TOU电价机制的调峰经济优化，明显提升了作为经济主导的运行收益。而在补偿收益方面，由于策略2、3均具有电量均衡模型，故在相同充/放电电量下得到的补偿收益持平，均比策略1提升了1.473%。

表5 各控制策略储能收益万元

Tab. 5 Energy storage benefits of each control strategy

控制策略	日均运行收益	日均补偿收益	日均环境收益
策略1	159.556	156.569	55.837
策略2	163.029	158.875	57.317
策略3	177.780	158.875	57.703

新窗口打开| 下载CSV

综上，策略3在策略2的基础上进行了调峰经济性优化及技术、经济权衡，虽然在负荷峰谷差、峰谷差率和标准差改善量等调峰技术性指标上稍逊于策略2，但其兼顾储能调峰技术性及经济性，并有助于缓解弃风消纳问题。策略3在日均弃风电量上相较于策略2减少了5.875 MW⋅h，增加了0.220万元的日风电收益，表明在达到一定调峰效果的同时，在其全寿命周期内仍保持较好的调峰经济性。综上可知，策略3更具优势。

为了比较同等规模的液流电池与锂电池储能调峰情况，同时也为验证本文优化策略在不同类型电池储能下的通用性和有效性，在策略3下对2种电池储能调峰情况进行对比分析，结果如表6所示。

表6 在策略3下ZBB与锂电池评价指标对比

Tab. 6 Comparison of ZBB and lithium battery evaluation index under strategy 3

类型	日均负荷峰谷差/MW	日均负荷峰谷差率/%	日均负荷标准差改善量/MW	储能净收益率/%	日均弃风电量/(MW⋅h)
无储能调节	972.311	16.287	—	—	6 216.138
ZBB	622.537	10.716	73.164	11.028	4 936.140
锂离子电池	596.620	10.314	74.784	7.710	5 029.286

新窗口打开| 下载CSV

由表6可知，锂电池储能在日均负荷峰谷差、峰谷差率及标准差改善量指标上均优于液流电池，这是因为锂电池的充放电效率高于液流电池，使其在高峰时段的放电功率较大，削峰效果更好；但同时锂电池的大功率放电也进一步挤占了风电并网空间，造成弃风电量增加了1.887%，风电并网收益损失3.493万元，并且在储能净收益率上降低了30.087%，弱于液流电池。

综上可知，锂电池储能在调峰技术性方面存在性能优势，但也因此增大了弃风电量，由于循环寿命短，在参与调峰的全寿命经济性方面存在劣势。

5 结论

1）在调峰技术性优化方面，所提策略相较于原负荷，在日均负荷峰谷差、峰谷差率指标上分别降低了35.973%和34.205%，相较于策略1分别优化提升了14.221%和14.650%，表明该策略进一步提升了调峰效果。

2）在调峰经济性优化方面，所提策略控制下的储能净收益率最高，分别较策略1、2提高了5.582%、3.783%，在具体收益上，以作为经济主导的运行收益提升效果最佳，分别较策略1、2提高了11.422%、9.048%，且合并缓解了电网弃风消纳问题，在达到一定调峰效果的同时，在其全寿命周期内仍保持较好的调峰经济性。

3）在辅助电网调峰场景下，虽然锂电池储能在技术上存在一定的性能优势，但是液流电池因具有更高的安全性和更长的循环寿命，在全寿命周期内表现出良好的经济性，故在储能市场上仍不可或缺。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

姜红丽，刘羽茜，冯一铭，等．

碳达峰、碳中和背景下“十四五”时期发电技术趋势分析

[J]．发电技术，2022，43(1)：54-64． doi:10.12096/j.2096-4528.pgt.21030