0 引言
笔者采用有限元软件ANSYS对NREL 5 MW单桩式海上风电机组进行整体建模,模拟分析塔筒在不同风速下的动力响应。在建立风电机组塔筒结构三维实体模型的基础上,同时施加了叶轮旋转作用与土构耦合作用。为全面考察不同叶轮转速对运行中机组塔筒动力响应的影响,选取6种风速工况,以及与之对应的叶轮转速进行分析,定量研究不同风速对塔筒动力学行为的影响。
1 风电机组计算模型
1.1 NREL 5 MW单桩式海上风电机组模型
图1
图1
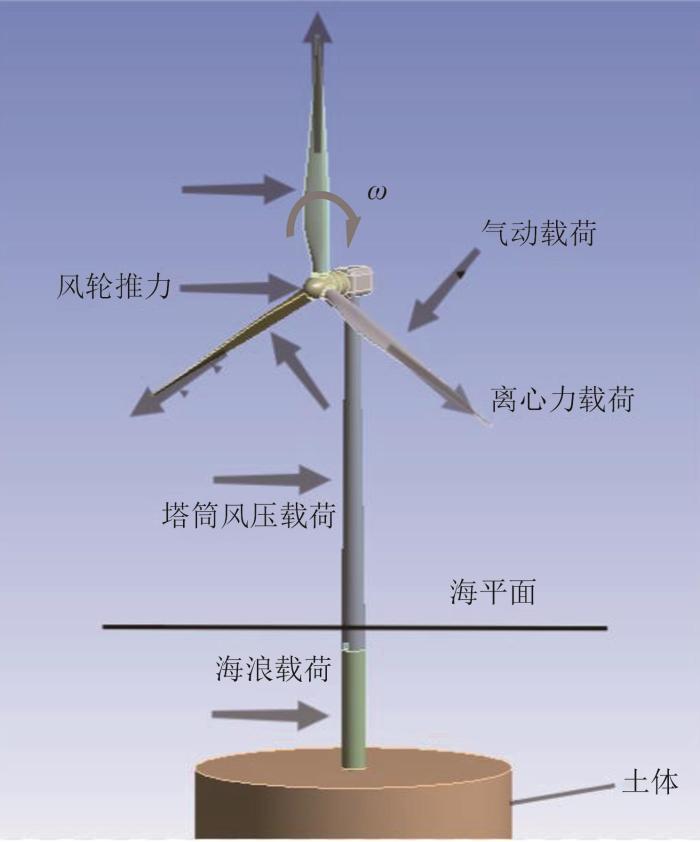
单桩式海上风电机组三维实体模型
Fig. 1
Three-dimensional solid model of monopile offshore wind turbine
表1 风电机组结构材料属性
Tab. 1
| 结构名称 | 密度/(kg/m3) | 杨氏模量/GPa | 泊松比 |
|---|---|---|---|
| 叶片 | 1 850 | 38 | 0.3 |
| 塔筒 | 7 850 | 210 | 0.3 |
| 单桩 | 7 850 | 210 | 0.3 |
表2 NREL 5 MW单桩式海上风电机组主要参数
Tab. 2
| 项目 | 参数 | 数值 |
|---|---|---|
| 基础描述 | 额定功率/MW | 5 |
| 切入、额定风速/( | 3、11.4 | |
| 额定转速/(r/min) | 12.1 | |
| 转子配置 | 3叶片 | |
| 叶片 | 转子直径/m | 126 |
| 轮毂高度/m | 100 | |
| 轮毂直径/m | 3 | |
| 叶片长度/m | 61.5 | |
| 塔筒 | 塔筒高度/m | 90 |
| 塔顶、塔底外径/m | 3.87、6 | |
| 塔顶、塔底壁厚/m | 0.027、0.054 | |
| 单桩 | 单桩长度/m | 75 |
| 单桩外径/m | 6 | |
| 单桩壁厚/m | 0.054 |
1.2 不同工况选取
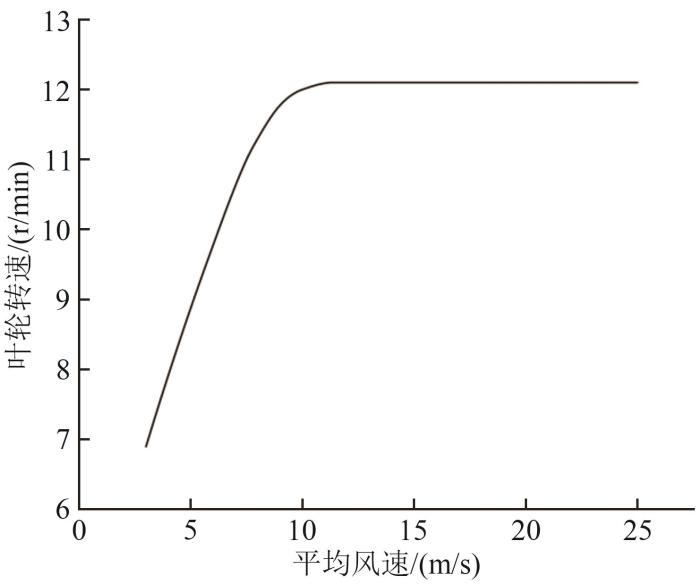
本文从NREL 5 MW风电机组切入风速3 m/s与切出风速25 m/s区间内,选取6种平均风速及与之对应的叶轮转速作为模拟工况,见表3,其中工况3为风电机组额定工况。风速与转速之间关系由
表3 6种模拟工况
Tab. 3
| 参数 | 工况1 | 工况2 | 工况3 | 工况4 | 工况5 | 工况6 |
|---|---|---|---|---|---|---|
| 平均风速/( | 3.0 | 7.2 | 11.4 | 16.0 | 20.4 | 25.0 |
| 叶轮转速/(r/min) | 6.9 | 9.6 | 12.1 | 12.1 | 12.1 | 12.1 |
式中:
图2
图2
平均风速与叶轮转速关系曲线
Fig. 2
Curve of relationship between average wind speed and impeller speed
由于实际风电机组有变桨系统,使得叶轮转速不会超过额定转速12.1 r/min,为使模拟结果接近工程实际,设置风速大于额定风速11.4 m/s的工况,即工况4—6中,叶轮转速保持为12.1 r/min。
1.3 单桩式海上风电机组结构运动数学模型
单桩式海上风电机组结构运动微分方程[15]表达式为
式中:
式中:
对系统进行模态分析时,视结构做无阻尼自由振动,方程
设方程
式中:
将
考虑叶轮旋转产生的动力刚化效应,需要通过静力计算向模态分析施加预应力:
将得到的刚度矩阵施加于模态分析微分方程,
式中结构整体刚度矩阵
这就是考虑叶轮旋转产生动力刚化效应的结构模态分析微分方程。同理,机组结构运动微分方程可以表示为
1.4 叶轮旋转作用的施加
风电机组运行时,叶轮的旋转与变形会导致叶片刚度增大,出现动力刚化效应。不同的叶轮转速对塔筒振动特性带来的影响也会有所区别[16]。将叶轮旋转产生的离心力作为预应力形成离心刚度矩阵,在进行有限元模拟时,将其叠加到机组模态和瞬态刚度矩阵上,以此来考虑叶轮旋转对塔筒动态特性产生的影响。
在叶轮以一定速度旋转时,叶片的应变张量 ε 为:
式中
动力刚化效应下的应力-应变关系[16]为
式中:
叶片在旋转过程中产生的离心力总和为
式中:r为叶片i点到转轴中心的距离,m;m(r)为单位长度质量,kg;
由叶片旋转引起的刚度矩阵表示为:
式中
为尽量提高模拟结果的真实度,在有限元模型中赋予叶片与轮毂2个部件初始旋转状态,而机舱、塔筒与单桩等结构由于在真实情况下并不旋转,因此没有考虑这些结构所形成的几何刚度矩阵。
1.5 土构耦合作用的施加
表4 海上风场土质实测参数
Tab. 4
| 参数 | 淤泥质粉质黏土 | 粉砂 | 粉质黏土 |
|---|---|---|---|
| 有效重度/( | 7.6 | 9.6 | 9.9 |
| 剪切波速/( | 110.0 | 190.0 | 210.0 |
| 剪切模量/MPa | 21. 7 | 70. 8 | 97. 2 |
| 弹性模量/MPa | 56. 4 | 184 | 252. 7 |
| 泊松比 | 0.3 | 0.3 | 0.3 |
桩土接触底部采用硬接触形式,侧向采用摩尔库伦摩擦罚函数形式,通过摩擦系数定义接触面关系,表述为
式中:
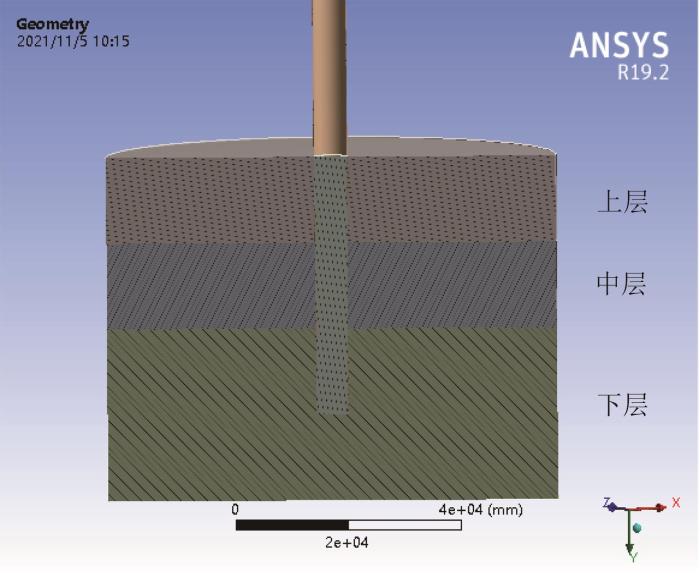
土体边界条件为:底边三向固定约束,外侧径向位移约束。模型中将单桩内部填充物考虑为混凝土。土体与单桩模型内部截面示意图如图3所示。
图3
图3
土体与单桩模型内部截面示意图
Fig. 3
Schematic diagram of the internal cross-section of the soil and monopile model
由于三维模型本身没有重力作用,土体模型内没有任何应力,并非现实中的初始状态。为减小模拟计算误差,在进行动态分析之前对土体模型进行初始的应力平衡。
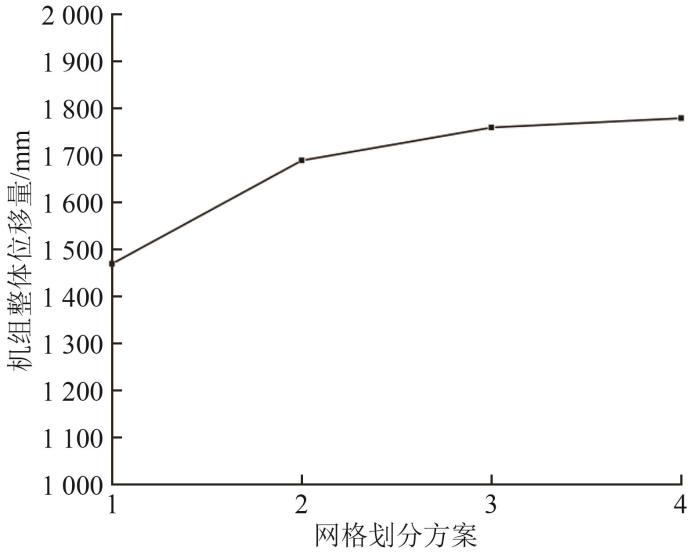
1.6 模型网格划分
为保证计算结果精度与计算效率,网格选择占用计算资源较少的四面体网格和质量较高的六面体网格相结合,在单桩与土体接触处细化网格[18]。由于土体模型结构简单、尺寸较大,且本文着重分析塔筒性能,因此设置土体模型网格尺寸大于机组结构网格尺寸。
表5 网格划分方案
Tab. 5
| 参数 | 方案1 | 方案2 | 方案3 | 方案4 |
|---|---|---|---|---|
| 机组网格尺寸/mm | 1 000 | 750 | 500 | 500 |
| 土体网格尺寸/mm | 2 000 | 2 000 | 2 000 | 1 000 |
| 总单元数 | 359 320 | 408 432 | 534 033 | 2 794 423 |
| 总节点数 | 515 230 | 593 260 | 805 936 | 3 868 600 |
| 平均元素质量 | 0.824 9 | 0.803 03 | 0.851 31 | 0.878 21 |
| 平均Skewness值 | 0.232 54 | 0.263 09 | 0.209 1 | 0.188 38 |
图4
2 载荷计算模型
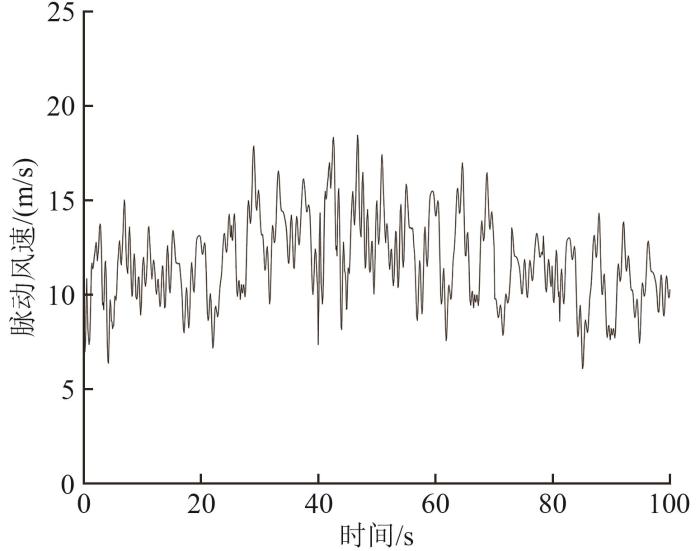
2.1 脉动风载荷
图5
图5
平均风速11.4 m/s时 100 s脉动风速分布图
Fig. 5
100 s distribution diagram of fluctuating wind speed when the average wind speed is 11.4 m/s
作用在风电机组上的风载荷值按式(
风剪切采用指数模型:
式中:Vh 为距地面h米处风速,m/s;
作用在塔筒的风压载荷[20]:
式中:
风轮水平轴向推力:
式中:
叶片气动载荷切向力:
式中
叶轮旋转力矩:
式中:
叶轮俯仰力矩:
式中:
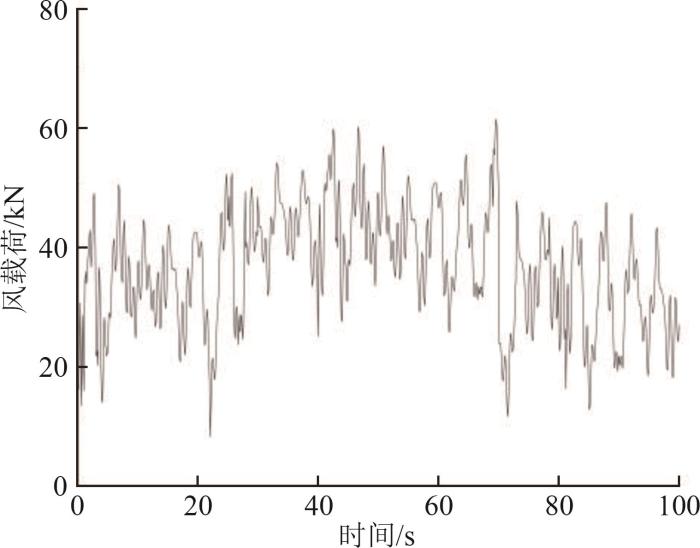
设置所有载荷总时长100 s,步长为0.1 s。由于篇幅限制,在此展示额定风速11.4 m/s下塔筒顶部脉动风载荷100 s时程曲线,如图6所示。
图6
图6
额定风速下塔筒顶部脉动风载荷100 s时程曲线
Fig. 6
100 s time history curve of fluctuating wind load at the top of the tower under rated wind speed
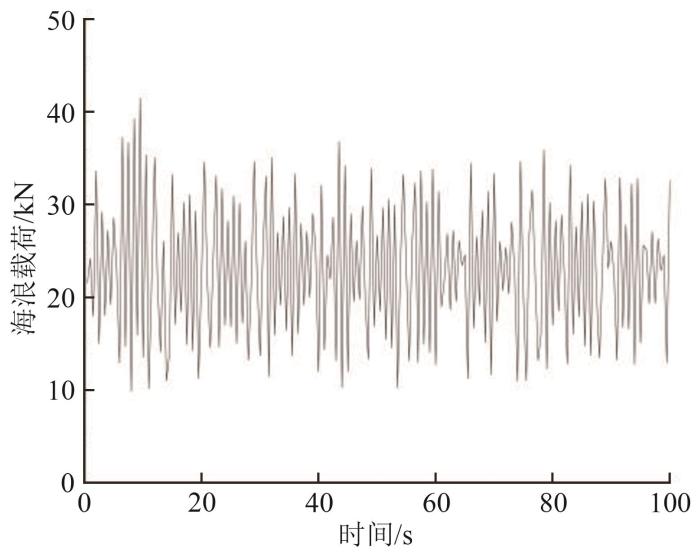
2.2 海浪载荷
式中:
由于单桩式海上风电机组是典型的高耸柔性结构,其自身的变形与位移会影响海浪中水质点的速度与加速度,因此要对式(
式中:
海浪载荷100 s时程曲线如图7所示。在本文模拟计算中,海浪载荷的施加位置在单桩高于海床之上的部分,即单桩结构在土体模型之上的部分。
图7
3 不同工况塔筒动态特性分析
3.1 模态特性分析
通过ANSYS Workbench软件Modal模块进行机组结构模态分析。施加不同转速的叶轮旋转初始状态,将旋转产生的离心力作为模态分析的预应力,然后形成离心刚度矩阵并将其叠加到模态刚度矩阵上,以此来考虑叶轮旋转产生的动力刚化效应对塔筒模态特性的影响。
由于工况3以后叶轮转速不再变化,动力刚化效应产生的刚度矩阵也不会变化,因此工况4、5、6下模态情况不予考虑。通过有限元计算,得到前3种工况下塔筒前六阶模态频率值,见表6。
表6 前3种工况下塔筒结构模态频率值
Tab. 6
| 模态阶数 | 叶片静止工况/Hz | 工况1计算值/Hz | 变化率/% | 工况2计算值/Hz | 变化率/% | 工况3计算值/Hz | 变化率/% |
|---|---|---|---|---|---|---|---|
| 一阶频率 | 0.154 92 | 0.159 51 | 2.966 | 0.163 74 | 5.697 | 0.169 28 | 9.27 |
| 二阶频率 | 0.158 08 | 0.162 62 | 2.869 | 0.166 67 | 5.431 | 0.172 36 | 9.03 |
| 三阶频率 | 0.643 33 | 0.646 74 | 0.531 | 0.648 99 | 0.880 | 0.649 57 | 0.97 |
| 四阶频率 | 0.735 98 | 0.740 37 | 0.597 | 0.742 10 | 0.832 | 0.743 50 | 1.02 |
| 五阶频率 | 0.890 43 | 0.902 10 | 1.310 | 0.911 10 | 2.321 | 0.954 75 | 7.22 |
| 六阶频率 | 1.364 94 | 1.410 45 | 3.334 | 1.421 00 | 4.107 | 1.437 70 | 5.33 |
由表6可知,在工况1下,塔筒前两阶固有频率增幅约为2.966%和2.869%;在工况2与工况3下,塔筒前两阶固有频率增幅便分别达到5.697%、5.431%、9.27%、9.03%。风速与转速的增加使塔筒结构模态频率与增幅都逐渐变大。这是因为叶片旋转产生了动力刚化效应,并且通过塔筒与叶片的耦合作用影响了固有频率,因此对塔筒动力特性进行分析时需要充分考虑风速与转速的影响。
3.2 位移响应特性分析
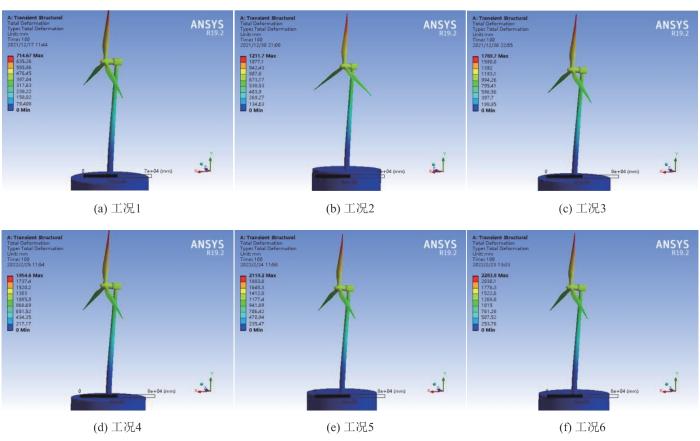
风电机组塔筒位移量是对其进行安全监测与评估分析的重要参量。通过Transient Structure模块进行机组结构瞬态位移响应分析。首先施加脉动风载荷与海浪载荷,进行静力学分析,然后通过APDL命令流将预应力几何刚度矩阵叠加到瞬态分析刚度矩阵上。得到不同工况下机组整体瞬态响应位移云图,如图8所示。
图8
图8
不同工况下机组整体瞬态响应位移云图
Fig. 8
Cloud diagram of the total displacement of the transient response of the overall unit under different simulation conditions
由图8可知,机组整体位移最大值出现在叶尖处,塔筒前后方向位移(x方向)与侧向位移(z方向)最大位移量均出现在塔筒顶部,下文着重分析顶部位移量。
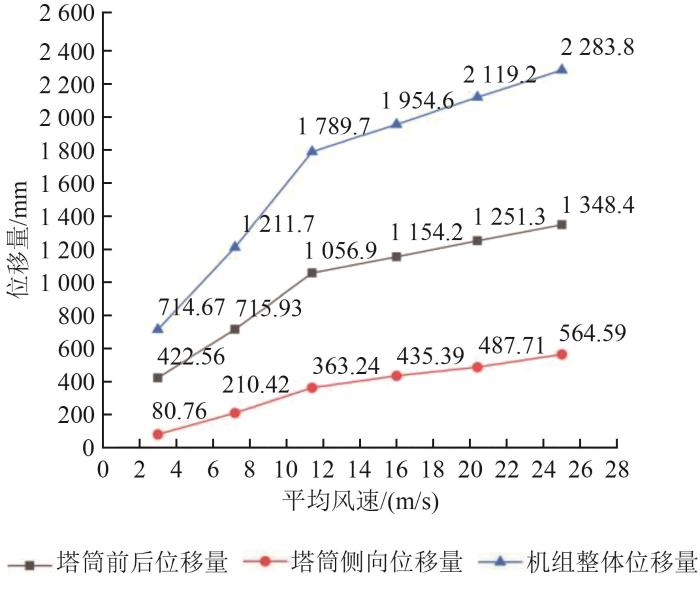
6种工况下位移量如图9所示。可以看出机组整体位移量与塔筒前后方向、侧向位移量都受风速和叶轮转速变化影响,随着风速与转速增加,位移量峰值增大,但增幅减小,位移量呈非线性增长趋势。
图9
图9
塔筒瞬态响应位移量随平均风速变化曲线
Fig. 9
Variation curve of tower transient response displacement with average wind speed
由图9可知,机组整体位移量变化最为明显,工况1到工况2位移量变化值为497.03 mm,增幅为69.55%;工况2到工况3位移量变化值为578 mm,增幅为47.7%;而在工况3之后位移变化量和增幅明显减小,位移量分别是164.9、164.6、164.6 mm,增幅分别减小为9.21%、8.42%、7.77%。
塔筒顶部前后方向瞬态响应位移量在工况1到工况2变化值为293.37 mm,增幅为69.43%;工况2到工况3位移量变化值为340.97 mm,增幅为47.63%;而在工况3之后位移变化量和增幅同样明显减小,位移量分别是97.3、97.1、97.1 mm,增幅分别减小为9.2%、8.41%、7.76%。塔筒顶部前后方向的位移量增幅与机组整体位移量增幅基本一致。
塔筒顶部侧向瞬态响应位移量在工况1到工况2变化值为129.66 mm,增幅为160.55%;工况2到工况3位移量变化值为152.82 mm,增幅为72.63%;而在工况3之后位移变化量分别为72.15、52.32、76.88 mm,增幅分别减小为19.86%、12.02%、15.76%。这说明叶片旋转速度与风速的变化会对塔筒顶部侧向瞬态响应位移量产生较大影响,但拟合曲线表明总体增长趋势与机组整体位移量、塔筒前后方向位移量基本相似。
3.3 等效应力响应特性分析
图10
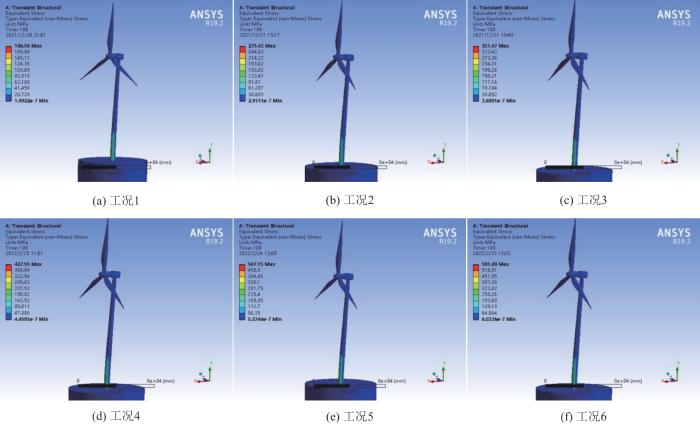
图10
不同工况下塔筒结构瞬态响应等效应力云图
Fig. 10
Equivalent stress cloud diagram of tower structure transient response under different working conditions
图11
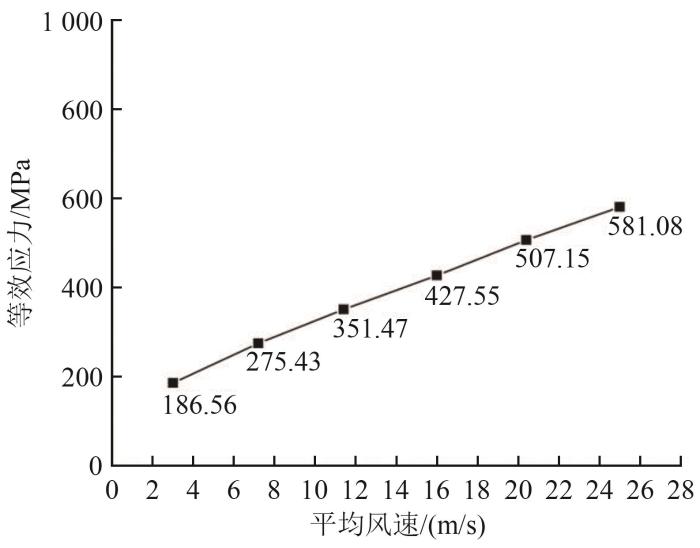
图11
塔筒瞬态响应等效应力值随平均风速变化曲线
Fig. 11
Variation curve of equivalent stress value of tower transient response with average wind speed
由图10可知,最大等效应力出现在塔筒底部与单桩处,此处为风电机组运行时较为危险的部位,在进行状态监测时应重点关注此处。
由图11可知,塔筒等效应力值随风速与转速的增加逐渐增大。但与塔筒位移量增长趋势不同,等效应力数值大致为线性增长,这说明风速对其变化起主要作用,而叶轮转速对其影响不大。这是由于在模拟叶轮旋转工况时赋予叶片与轮毂2个部件初始旋转状态,而叶轮旋转工况需要通过与塔筒结构的相互作用才能影响到塔筒的动态特性。因此叶轮旋转工况对塔筒顶部的位移量变化影响较大,而对等效应力值的影响会被塔筒这个高柔性结构减弱。
3.4 疲劳损伤特性分析
图12
图13
图13
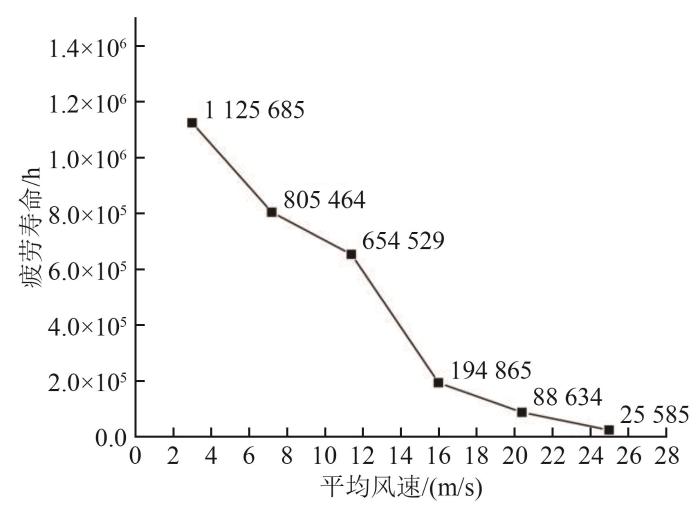
塔筒结构疲劳寿命随平均风速变化曲线
Fig. 13
Variation curve of fatigue life of tower structure with average wind speed
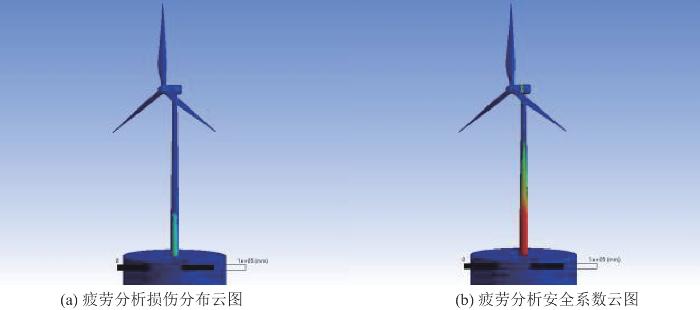
额定工况下塔筒疲劳损伤分布云图与疲劳安全系数云图如图14所示。可以看出,疲劳损伤与安全系数危险值主要分布在塔筒底部与单桩处,与最大等效应力分布位置吻合。
图14
图14
塔筒结构疲劳损伤分布与安全系数云图
Fig. 14
Fatigue damage distribution and safety factor cloud map of tower structure
4 结论
通过有限元模拟,在考虑桩基土构耦合作用下,分析研究了不同转速工况对单桩式海上风电机组塔筒振动特性的影响,其中包括塔筒模态特性、机组整体瞬态响应总位移量、塔筒瞬态响应前后方向与侧向位移量,以及等效应力值。模拟分析得到结论如下:
1)风速与叶轮转速的增加会使塔筒自振频率逐渐增大,且增幅也有所增加,其中最为明显的是前两阶模态频率,先前忽略风速变化的研究可能会导致模态频率结果不够准确;在进行机组设计时应考虑塔筒自振频率的增大,避开共振区域。
2)随着风速和叶轮转速的增加,结构位移量峰值增大,但增幅减小,位移量变化曲线总体呈非线性增长趋势;叶轮转速的变化对塔筒动态特性影响要大于风速的变化。
3)随着风速和叶轮转速的增加,等效应力值的峰值逐渐增大,但增幅并未与位移量增幅一致,等效应力数值大致为线性增长;最大等效应力出现在塔筒底部与单桩处,针对此应力集中现象,可以进行结构优化,以减小应力、位移,使结构的应力分布更加均匀,增加结构稳定性,在进行机组状态监测时应重点关注此处。
4)随着风速和叶轮转速的增加,塔筒疲劳寿命大幅下降,但都远超实际工作时长;塔筒结构疲劳损伤与安全系数最大值主要分布在塔筒底部与单桩处,与最大应力分布位置吻合,在设计时应优化此处结构疲劳强度。
参考文献
我国海上风电发展关键技术综述
[J].
Review on key technologies of offshore wind power development in China
[J].
半潜式海上风力机流固耦合特性分析
[J].
Analysis of fluid-structure coupling characteristics of semi-submersible offshore wind turbine
[J].
海上风电的发展现状与前景展望
[J].
Development status and prospect of offshore wind power
[J].
气动力和离心力对风力机叶片应力影响研究
[J].
Effect of aerodynamic force and centrifugal force on wind turbine blade stress
[J].
大型风力发电机旋转叶片结构动力特性分析
[J].
Analysis of dynamic characteristics of rotating blade structure of large wind turbine
[J].
基于VMD方法的海上风力机结构TMD抗震
[J].
TMD seismic resistance of offshore wind turbine structure based on VMD Method
[J].
MW级风电机组钢筋混凝土塔筒稳定性分析
[J].
Stability analysis of reinforced concrete tower for MW wind turbine
[J].
Application of differential transformation method for free vibration analysis of wind turbine
[J].
基于TMD的风力机塔筒振动控制研究
[J].
Vibration control of wind turbine tower based on TMD
[J].
Aerodynamics of leading-edge protection tapes for wind turbine blades
[J].
Modal decomposition of the dynamic response of wind turbine during one year of continuous monitoring
[J].
考虑土-结构动力相互作用的冷却塔地震响应分析
[J].
Seismic response analysis of Cooling tower considering soil-structure dynamic interaction
[J].
考虑土-结相互作用大型风力发电结构风致响应分析
[J].
Wind-induced response analysis of large wind power generation structure considering soil-junction interaction
[J].
Dynamic analyses of operating offshore wind turbines including soil structure interaction
[J].
基于等效梁基础模型的海上风机基础动力响应研究
[D].
Research on dynamic response of offshore fan foundation based on equivalent beam foundation model
[D].
考虑叶片旋转及土-结构相互作用对风电结构动力特性影响的研究
[J].
Study on effects of blade rotation and soil-structure Interaction on dynamic characteristics of wind power structures
[J].
基于精确桩土模型的桁架式大型海上风力机地震动力学响应分析
[J].
Seismic dynamic response analysis of trussed large offshore wind turbine based on precise pile-soil model
[J].
风力发电塔架的动态响应分析
[D].
Dynamic response analysis of wind power tower
[D].
大型风力发电机组塔筒载荷特性分析
[D].
Analysis of load characteristics of large wind turbine tower
[D].
波浪与地震荷载共同作用下桩的动力响应
[J].
Dynamic response of piles under wave and seismic loads
[J].
The force exerted by surface waves on piles
[J].
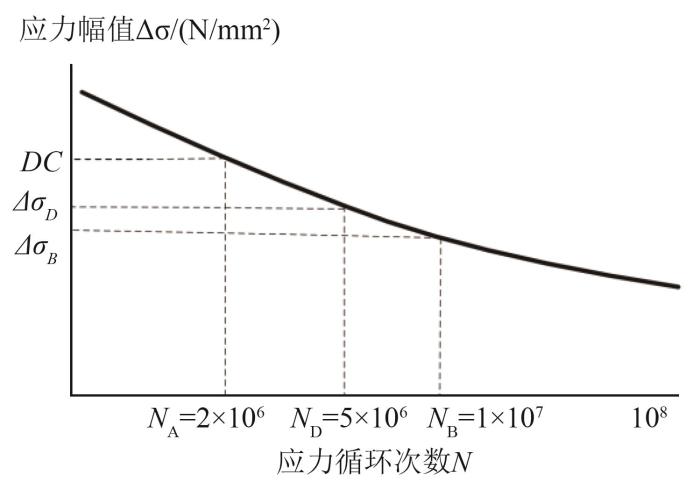
Recommendations for fatigue design of welded joints and components
[J].