考虑经济性和可靠性的抗灾型骨干网架规划方法

doi:10.12096/j.2096-4528.pgt.21013

考虑经济性和可靠性的抗灾型骨干网架规划方法

罗春辉¹, 邹同华¹, 瞿纲举¹, 汤涛²

1.湖南省送变电工程有限公司, 湖南省长沙市 410015

2.智能电网运行与控制湖南省重点实验室(长沙理工大学), 湖南省长沙市 410114

A Planning Method for Anti-disaster Backbone Grid Considering Economy and Reliability

LUO Chunhui¹, ZOU Tonghua¹, Gangju QU¹, TANG Tao²

1.Hunan Electric Power Transmission and Transformation Engineering Co. , Ltd. , Changsha 410015, Hunan Province, China

2.Hunan Province Key Laboratory of Smart Grids Operation and Control (Changsha University of Science and Technology), Changsha 410114, Hunan Province, China

收稿日期: 2022-11-26

基金资助:

国家自然科学基金项目.  51737002
湖南省自然科学基金项目.  2020JJ5584
湖南省教育厅创新平台开放基金项目.  19K003

Received: 2022-11-26

作者简介 About authors

罗春辉(1991)，男，硕士，工程师，研究方向为电网差异化规划、电动汽车入网(V2G)关键技术、面向园区微网的综合能源系统运行规划、电力经济与电力市场，chluo@hnu.edu.cn；

邹同华(1994)，男，硕士，助理工程师，主要研究方向为输变电工程项目管理、电力系统规划与可靠性，zouth@hnu.edu.cn；

瞿纲举(1975)，男，教授级高级工程师，研究方向为面向大电网安全的系统保护、阻断连锁故障蔓延的故障预警和主动保护、电力线路故障测距与定位，285727525@qq.com；

汤涛(1989)，男，博士，讲师，研究方向为小电流接地系统故障选线与定位、智能配电网单相接地故障保护，ttqzh0102@163.com。

摘要

建设抗灾型骨干网架对增强极端自然灾害下电力系统的供电能力具有重要意义。为此，提出一种兼顾经济性和可靠性的抗灾型骨干网架规划方法。首先，采用全寿命周期内的加固成本和减损效益来表征规划方案的经济性和可靠性，以骨干网架单位加固成本对原始网架产生的单位减损效益最大为目标函数，并以网络拓扑连通性和系统安全运行为刚性约束，构建抗灾型骨干网架优化模型。其次，通过改进的纵横交叉优化(improved crisscross optimization，ICSO)算法求解该模型，寻求最优规划方案。最后，通过IEEE 30节点系统的仿真分析验证了所提方法的有效性。

关键词： 电网规划 ; 抗灾型骨干网架 ; 全寿命周期成本 ; 纵横交叉优化(CSO)

Abstract

The construction of anti-disaster backbone grid is of great significance to enhance the power supply capacity of power system under extreme natural disasters. Comprehensively considering economy and reliability, a planning method for anti-disaster backbone grid was proposed. The economy and reliability of the planning scheme were expressed as the strengthened cost and the benefit from loss reduction in life cycle. The objective function was to maximize the unit benefit from loss reduction of the original grid caused by the unit strengthened cost of backbone grid. Taking the network connectivity and safe operation of power system into account, a planning model for anti-disaster backbone grid was established. The model was solved by the improved crisscross optimization (ICSO) algorithm to find the optimal planning scheme. Finally, the effectiveness of the proposed method was verified by the simulation analysis of the IEEE 30-bus system.

Keywords： power grid planning ; anti-disaster backbone grid ; life cycle cost ; crisscross optimization (CSO)

PDF (2035KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

罗春辉, 邹同华, 瞿纲举, 汤涛. 考虑经济性和可靠性的抗灾型骨干网架规划方法. 发电技术[J], 2023, 44(3): 425-430 DOI:10.12096/j.2096-4528.pgt.21013

LUO Chunhui, ZOU Tonghua, Gangju QU, TANG Tao. A Planning Method for Anti-disaster Backbone Grid Considering Economy and Reliability. Power Generation Technology[J], 2023, 44(3): 425-430 DOI:10.12096/j.2096-4528.pgt.21013

0 引言

近年来，我国电网屡次因冰冻、地震、山火、台风等极端自然灾害遭受破坏，造成了严重的国民经济损失和社会影响^[1]。如2008年初的南方冰灾在全国范围内造成了大面积变电站和线路停运以及输电线路铁塔倒塌，直接经济损失超过1 500亿元^[2]。电力元件的设防标准无法抵御灾害强度，是极端自然灾害导致大停电事故的主要原因。因此，从电网规划的角度提高骨干网架的抗灾标准，确保极端灾害发生时骨干网架正常运行，从而保障关键负荷持续供电，对当前建设坚强智能电网具有重要的现实意义。如何合理规划抗灾型骨干网架，是目前我国电网亟待解决的关键问题之一。

目前，国内外学者均对抗灾型骨干网架的规划问题进行了相关研究。文献[3]提出了评价电网中重要元件的关键环节辨识方法，该方法对规划骨干网架具有指导意义。文献[4]为提高灾害情况下电网的容灾能力，从指导原则、优化模型、求解方法和实施步骤等方面提出了完整的规划流程。文献[5-6]对抗灾型骨干网架规划的经济效益进行了量化研究，研究结果对差异化规划的经济性评估具有一定参考意义。文献[3-6]对抗灾型电网差异性规划的经济性和可靠性各有侧重。文献[7]在抗灾规划的效益评估中计及了极端灾害对缺电成本的影响和线路故障后的维修成本，可有效兼顾经济性与可靠性。然而上述研究均忽视了设备的使用寿命，不具备电网常规性规划的全寿命周期特点，难以保证规划后电网长时间尺度的经济性和可靠性折中最优。

由于要综合考虑网络拓扑连通性约束、潮流约束、系统安全运行约束，抗灾型骨干网架的寻优属于非线性离散优化问题。数学优化方法在大电网的分析计算中往往存在维数灾问题，计算量大，速度慢，且对初始解较敏感，不利于搜索全局最优解。智能算法因其独特智能特性，在求解此类电力系统优化问题中应用广泛^[8-9]。纵横交叉优化(crisscross optimization，CSO)算法是近些年发展起来的一种智能算法，与其他智能算法相比，在全局收敛能力和收敛速度方面优势明显，目前已应用于多种电力系统优化问题，如经济调度^[10]、故障定位^[11]等，但也存在收敛精度不够的缺陷。

本文提出一种考虑经济性和可靠性的抗灾型骨干网架规划方法，构建了抗灾型骨干网架优化模型，采用改进的CSO (improved CSO，ICSO)算法求解该模型，寻求最优规划方案。最后，通过IEEE 30节点系统的算例仿真验证该方法的可行性和有效性。

1 全寿命周期成本效益评价指标

本文着眼于抗灾型骨干网架规划的长时间尺度，考虑网架规划全寿命周期的经济性和可靠性，并借鉴灾害经济学中“有无对比”计算原理，提出抗灾型骨干网架规划全寿命周期成本效益评价指标，以表征规划方案的经济性和可靠性。

1.1 经济性指标

抗灾型骨干网架规划的经济性方面主要考虑提高电网设防标准后的加固成本，即骨干网架全寿命周期的投资、运维和报废成本。其中：投资成本为提高骨干网架设计标准在规划初期增加的一次性投入成本；运维成本为电网运行阶段产生的人工费用及能源损耗等；报废成本为电力元件寿命周期结束时的处理成本和残值^[12]。考虑资金的时间价值，将投资成本和报废成本按等年值法进行计算。本文建立的经济性指标可表示为

\begin{array}{l} C_{L C C} = \frac{r {(1 + r)}^{N}}{r {(1 + r)}^{N} - 1} \sum_{i \in Ω} k_{i} x_{i} l_{i} + λ_{1} \sum_{i \in Ω} k_{i} x_{i} l_{i} + \\ \frac{r}{r {(1 + r)}^{N} - 1} [λ_{2} - \frac{1}{{(1 + s)}^{N}}] \sum_{i \in Ω} k_{i} x_{i} l_{i} \end{array}

(1)

式中：C_LCC为提高电网设防标准后的加固成本；Ω为规划范围内的线路集合；k_i 为第i条线路的投切状态，1表示投入，0表示切除；x_i 为第i条线路一次性投入的单位成本；l_i 为第i条线路的长度； $λ_{1}$ 为运维成本相对于一次性投入成本的折算系数； $λ_{2}$ 为处理成本和残值相对于一次性投入成本的折算系数；s为年均折旧系数；N为规划周期；r为资金年利率。式(1)等号右边3项依次为按等年值法折算后的投资成本、运维成本和报废成本。

1.2 可靠性指标

抗灾型骨干网架规划的可靠性方面主要考虑发生极端自然灾害时，规划抗灾型骨干网架后电网的坚强程度。与规划前的电网相比，在极端自然灾害发生时的减损效益越大，表明电网的可靠性越高。减损效益包含直接效益和间接效益，其中：直接效益主要由减免灾况抢修费用、关键负荷和普通负荷的保障效益、电网公司向发电公司支付因非计划停机而产生的违约费构成；间接效益主要由社会救援费、重要负荷赔偿和隐形社会效益构成，间接效益可按直接效益乘以系数进行估算^[13]。本文建立的可靠性指标可表示为

\begin{array}{l} D_{L C C} = \sum_{i \in Ω} k_{i} y_{i} l_{i} + (P_{1} + P_{2}) g T + λ_{3} (P_{1} + P_{2}) g T + \\ (δ_{1} P_{1} + δ_{2} P_{2}) g T \end{array}

(2)

式中：D_LCC为骨干网架加固后极端灾害场景下的减损效益；y_i 为未加强建设标准时抢修在灾害中受损的重要电力线路i的单位费用； $λ_{3}$ 为电网公司向发电公司支付因非计划停机产生的违约费折算系数； $δ_{1}$ 和 $δ_{2}$ 分别为关键负荷和普通负荷的保障系数；P₁和P₂分别为灾害导致的关键负荷与普通负荷损失量；g为电网公司的售电电价与发电公司的上网电价之差；T为故障恢复时间。式(2)等号右边4项依次为抢修费用、各类负荷保障效益、电网公司赔偿费用和间接效益。

2 抗灾型骨干网架规划模型

抗灾型骨干网架规划采用全寿命周期内的加固成本和减损效益来表征规划方案的经济性和可靠性，以骨干网架的单位加固成本对原始网架产生的单位减损效益最大为目标函数，并将网络拓扑连通性和系统安全运行作为刚性约束，筛选出需要保留的线路和节点。因此，抗灾型骨干网架规划的数学模型表示为

\{\begin{array}{l} m a x F = (D_{L C C} / b_{0}) / (C_{L C C} / b_{1}) \\ s . t . b_{0} = \sum_{i = 1}^{n_{v}} k_{i} l_{i} \\ b_{1} = \sum_{i = 1}^{n_{w}} k_{i} l_{i} \\ ϕ (k) = 1 \\ g (x, S_{G L}) = 0 \\ h (x, S_{G L}) \leq 0 \end{array}

(3)

式中： $b_{0}$ 和 $b_{1}$ 分别为原始网架和骨干网架的线路总长； $n_{v}$ 和 $n_{w}$ 分别为原始网架和规划骨干网架的线路数； $k$ 为线路投入和切除的状态向量， $ϕ (k)$ 为拓扑连通性判别函数， $ϕ (k) = 1$ 表示所有子网络无孤立节点； $x$ 为系统运行状态向量； $S_{G L}$ 为节点注入功率向量； $g (x, S_{G L})$ 反映了系统的潮流约束； $h (x, S_{G L})$ 反映了系统的安全运行约束。

式(3)即考虑经济性和可靠性的抗灾型骨干网架规划的完整数学模型，该模型属于非线性离散优化问题，本文采用ICSO算法进行求解，以寻求最优的抗灾型骨干网架规划方案。

3 基于ICSO算法的骨干网架搜索

3.1 CSO算法基本原理

CSO算法作为群智能算法的一种，其具有横向交叉与纵向交叉呈链式反应的双搜索机制，与其他群智能优化算法的单搜索机制相比，在解决复杂优化问题(如含众多局部最优点的多模问题等)时，全局收敛能力和收敛速度优势明显^[14]。

1）横向交叉操作

\begin{array}{l} M_{h c} (j_{1}, d) = μ_{1} X (j_{1}, d) + (1 - μ_{1}) X (j_{2}, d) + \\ η_{1} [X (j_{1}, d) - X (j_{2}, d)] \end{array}

(4)

\begin{array}{l} M_{h c} (j_{2}, d) = μ_{2} X (j_{2}, d) + (1 - μ_{2}) X (j_{1}, d) + \\ η_{2} [X (j_{2}, d) - X (j_{1}, d)] \end{array}

(5)

式中：j₁和j₂为种群中的相异个体；d为解向量维度； X 和 M_hc分别为父种群和子种群； $μ_{1}$ 和 $μ_{2}$ 为区间[0,1]上均匀分布的随机数； $η_{1}$ 和 $η_{2}$ 为区间[-1,1]上的随机数。

2）纵向交叉操作

M_{v c} (j_{1}, d_{1}) = μ_{3} X (j_{1}, d_{1}) + (1 - μ_{3}) X (j_{1}, d_{2})

(6)

式中： $M_{v c}$ 为纵向交叉后的子种群； $d_{1}$ 、 $d_{2}$ 为解向量的不同维度； $μ_{3}$ 为区间 $[0,1]$ 上均匀分布的随机数。

横向交叉操作利于种群进化的多样性，纵向交叉操作可有效避免寻优过程陷入局部最优。但交叉操作缺少寻优方向引导，搜索效率有待提高；另外，恒定的纵向交叉因子不利于充分影响个体的自我认知行为，对种群信息的态势感知能力差。

3.2 CSO算法的改进

1）改进横向交叉操作

\{\begin{array}{l} X_{c o n, j}^{t + 1} = X_{c o n, j}^{t} + ω_{j}^{t} (X_{c o n, b}^{t} - X_{c o n, j}^{t}) \\ ω_{j}^{t} = ω_{m i n} + (ω_{m a x} - ω_{m i n}) \frac{f_{b}^{t} - f_{j}^{t}}{f_{b}^{t} - f_{w}^{t}} \end{array}

(7)

式中： $X_{c o n, b}^{t}$ 和 $X_{c o n, j}^{t}$ 分别为 $t$ 代种群中最优个体和个体 $j$ 的矢量； $ω_{m a x}$ 和 $ω_{m i n}$ 分别为扰动因子 $ω_{j}^{t}$ 的上、下限； $f_{j}^{t}$ 为 $t$ 代种群中个体 $j$ 的适应度； $f_{b}^{t}$ 和 $f_{w}^{t}$ 分别为 $t$ 代种群中的最优和最劣适应度。差分矢量 $X_{c o n, b}^{t} - X_{c o n, j}^{t}$ 对交叉操作的寻优方向具有较好的方向引导作用。

2）改进纵向交叉操作

\{\begin{array}{l} Z_{v c}^{t} = Z_{v c, m a x} + γ^{t} (Z_{v c, m a x} - Z_{v c, m i n}) \\ γ^{t} = \{\begin{array}{l} \frac{| f_{j_{1}}^{t} - \frac{1}{G - 1} \sum_{j_{2} = 1, j_{2} \neq j_{1}}^{G} f_{j_{2}}^{t} |}{f_{w}^{t} - f_{b}^{t}}, f_{w}^{t} - f_{b}^{t} \neq 0 \\ γ^{t - 1} μ_{4}, f_{w}^{t} - f_{b}^{t} = 0 \end{array} \end{array}

(8)

式中： $Z_{v c}^{t}$ 为纵向交叉因子； $γ^{t}$ 为自适应调整参数； $Z_{v c, m a x}$ 和 $Z_{v c, m i n}$ 分别为纵向交叉因子的最大值和最小值；G为种群规模； $μ_{4}$ 为区间 $[0,1]$ 上均匀分布的随机数。

纵向交叉操作的关键影响因素为纵向交叉因子 $Z_{v c}^{t}$ ，其直接决定参与纵向交叉的维数，其值应随种群信息自适应变化。

3.3 基于ICSO算法的骨干网架搜索步骤

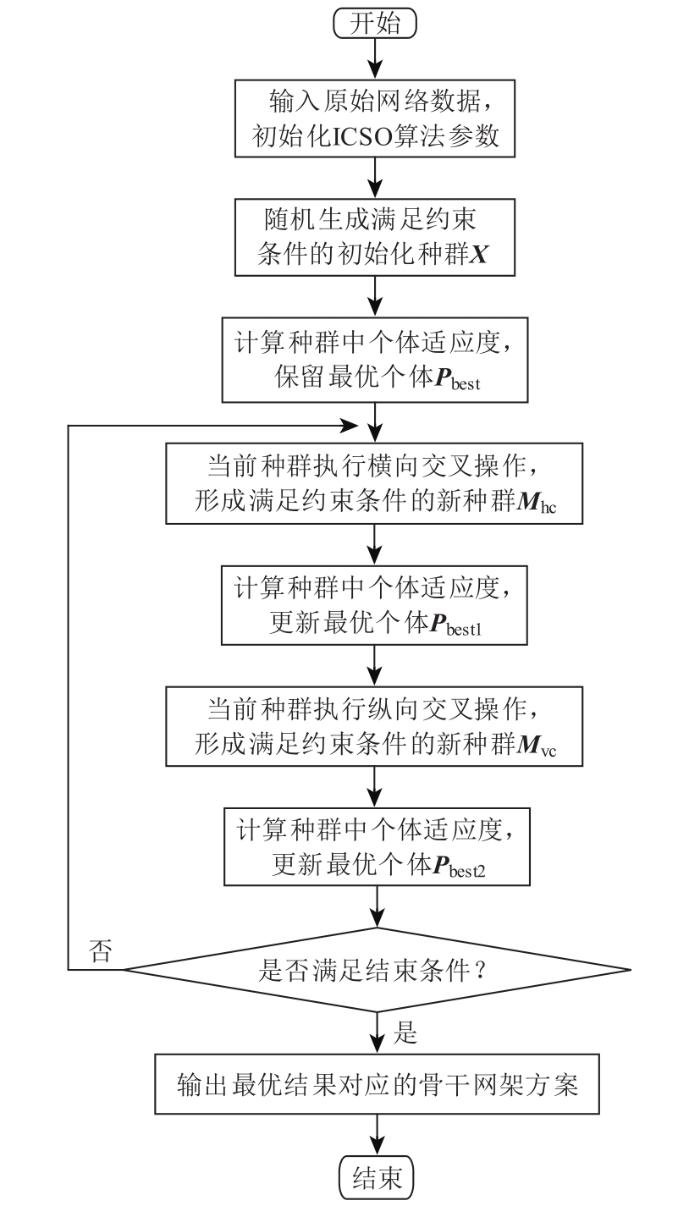
以式(3)中目标函数值的倒数1/F作为ICSO算法中的f，线路的投切状态向量 k 作为解向量，基于ICSO算法的骨干网架搜索流程如图1所示。具体步骤如下：

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 基于ICSO算法的骨干网架搜索流程

Fig. 1 Backbone network search process based on ICSO algorithm

1）输入所规划网架的各节点注入功率、线路参数等原始数据，初始化ICSO算法参数，生成满足约束条件的初始种群 X。

2）计算种群中的个体适应度，保留个体适应度最小值对应的解 P_best，即最优个体。

3）对当前种群执行横向交叉操作，如有个体不满足约束条件，则重新生成该个体，直至满足约束条件，计算该个体适应度，当得到所有个体满足约束条件的新种群 M_hc时，更新最优解 P_best1。

4）对当前种群执行纵向交叉操作，如有个体不满足约束条件，则重新生成该个体，直至满足约束条件，计算该个体适应度，当得到所有个体满足约束条件的新种群 M_vc时，更新最优解 P_best2。

5）若程序满足优化结束条件，则输出最优结果对应的骨干网架方案，优化过程结束，否则返回执行步骤3）。

4 算例分析

为验证所提方法的有效性，结合湖南地区的极端自然灾害发生情况和区域电网的网架特征，主要考虑冰灾影响，针对IEEE 30节点系统，考虑经济性和可靠性，基于ICSO算法进行骨干网架规划。

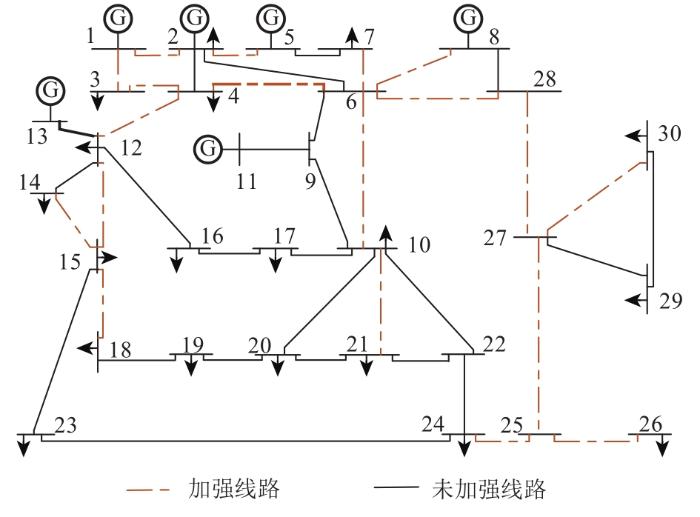
该系统含30个节点和41条支路，其中包含6个发电机节点，假定负荷节点中除节点16、17、19、20、22、23、25、26、29、30为普通负荷外，其余节点均为关键负荷。由于算例的原始数据中无线路长度，而线路电抗值与线路长度成正比，因此将线路总长度等效为线路总电抗值的标幺值，以便进行方案对比。设r=0.05，g=500元/(MW·h)， $λ_{1}$ =0.11， $λ_{2}$ =0.04，s=0.1， $δ_{1}$ =100， $δ_{2}$ =10， $λ_{3}$ =0.5。骨干网架的抗灾规划标准由30年一遇提高至50年一遇，根据工程经验，线路的单位造价约提高至312.57万元/km，增幅达200%^[15]。

仿真环境：系统软件Windows10 x64，内存8 GB，CPU为Intel Core i7，主频1.8 GHz，采用MATLAB R2010b编程。ICSO算法参数设置：种群规模为100，横向交叉因子为1，扰动因子上、下限分别为0.7和0.1，自适应纵向交叉因子上、下限分别为0.8和0.2，迭代次数为100。

图2为IEEE 30节点系统采用本文方法规划后的方案图。该骨干网架方案由19个节点和19条支路构成，其中包含4个发电机节点和17个关键负荷节点。规划后的电网灾后所能保留的负荷中85%为关键负荷，15%为普通负荷。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 IEEE 30节点系统骨干网架最优规划方案

Fig. 2 Optimal planning scheme of IEEE 30-bus backbone network

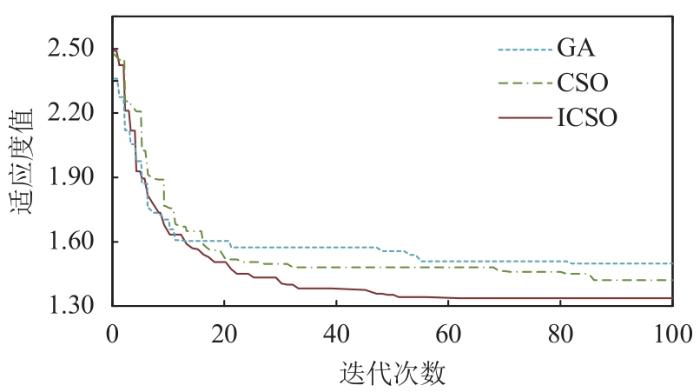
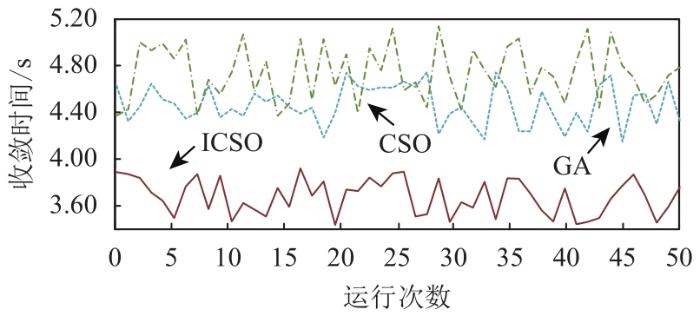
为验证ICSO算法的优越性，采用遗传算法(genetic algorithm，GA)和基本CSO算法分别进行骨干网架寻优。3种算法的种群规模和最大迭代次数设置一致，均独立运行50次，各自最优收敛曲线见图3，获得最优解的收敛时间如图4所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 不同算法最优方案的收敛曲线比较

Fig. 3 Convergence curve comparison of optimal schemes of different algorithms

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 不同算法最优方案的收敛时间比较

Fig. 4 Convergence time comparison of optimal schemes of different algorithms

由图3、4可知，ICSO算法比另2种算法收敛性更优，体现在获得最优解的适应度值更小和收敛时间更短2个方面，尤其是相比于基本CSO算法，改进的横向交叉操作和自适应纵向交叉因子使算法的寻优效率和全局寻优能力得到明显提升。随着计算规模增大，该方法的优越性将更加突出。

5 结论

1）基于抗灾型骨干网架规划的经济性和可靠性指标，构建了网架规划优化模型，该模型能够较好兼顾网架构建的经济性和可靠性，为抗灾型骨干网架规划提供了合理方案。

2）通过改进横向交叉操作和纵向交叉因子来增强ICSO算法对最优规划方案的搜索能力，与GA算法和基本CSO算法的寻优对比分析结果表明，采用ICSO算法求解网架规划优化模型具有更高的收敛效率和全局收敛能力。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

卢赓，邓婧，王渝红，等．

电力系统受极端天气的影响分析及其适应策略

[J]．发电技术，2021，42(6)：751-764． doi:10.12096/j.2096-4528.pgt.21059