基于主成分分析和深度神经网络的声学层析成像温度分布重建

doi:10.12096/j.2096-4528.pgt.21084

基于主成分分析和深度神经网络的声学层析成像温度分布重建

张立峰, 李晶, 王智

华北电力大学自动化系，河北省保定市 071003

Reconstruction of Temperature Distribution by Acoustic Tomography Based on Principal Component Analysis and Deep Neural Network

ZHANG Lifeng, LI Jing, WANG Zhi

Department of Automation, North China Electric Power University, Baoding 071003, Hebei Province, China

收稿日期: 2022-01-10

基金资助:

国家自然科学基金项目. 61973115

Received: 2022-01-10

作者简介 About authors

张立峰(1979)，男，博士，副教授，主要研究方向为火电厂先进测量技术，lifeng.zhang@ncepu.edu.cn；

李晶(1995)，女，硕士研究生，主要研究方向为声学层析测温；

王智(1998)，男，硕士研究生，主要研究方向为深度学习及其应用。

摘要

为快速准确地获取火电厂锅炉炉膛温度场在线监测信息，提出了一种基于深度神经网络(deep neural network，DNN)的声学层析成像(acoustic tomography，AT)温度场重建算法。对测量值进行归一化处理后，结合主成分分析(principal component analysis，PCA)降维，构建全连接网络区别峰型，分别搭建DNN与BP神经网络对归一化慢度值及其最值进行预测，最后重建温度场分布。采用该方法对4种典型的温度场模型进行了仿真，结果表明：DNN算法的重建质量优于Tikhonov正则化算法与共轭梯度算法，重建图像的平均相对误差和均方根误差分别小于0.36%和0.85%。

关键词： 火电厂 ; 电站锅炉 ; 温度场 ; 声学层析成像(AT) ; 深度神经网络(DNN) ; 主成分分析(PCA)

Abstract

In order to obtain the online monitoring information of boiler furnace temperature field in thermal power plant quickly and accurately, a temperature field reconstruction algorithm of acoustic tomography (AT) based on deep neural network (DNN) was proposed. After normalizing the measured values, combined with principal component analysis (PCA) dimension reduction, a fully connected network was constructed to distinguish the peak type. Moreover, DNN and BP neural network were built to predict the normalized slowness value and its maximum value, respectively. Finally, the temperature field distribution was reconstructed. Four typical temperature field models were simulated by using this method. The results show that the reconstruction quality of DNN algorithm is better than that of Tikhonov regularization algorithm and conjugate gradient algorithm. In addition, the average relative error and root mean square error of reconstructed image are less than 0.36% and 0.85% respectively.

Keywords： thermal power plant ; power plant boiler ; temperature field ; acoustic tomography (AT) ; deep neural network (DNN) ; principal component analysis (PCA)

PDF (1804KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

张立峰, 李晶, 王智. 基于主成分分析和深度神经网络的声学层析成像温度分布重建. 发电技术[J], 2023, 44(3): 399-406 DOI:10.12096/j.2096-4528.pgt.21084

ZHANG Lifeng, LI Jing, WANG Zhi. Reconstruction of Temperature Distribution by Acoustic Tomography Based on Principal Component Analysis and Deep Neural Network. Power Generation Technology[J], 2023, 44(3): 399-406 DOI:10.12096/j.2096-4528.pgt.21084

0 引言

实现电站锅炉炉膛温度的准确监测对火电厂的安全生产与稳定运行具有重要意义^[1-3]。受锅炉尺寸、炉内环境恶劣等因素影响，传统测温方法(如热电阻测温、热电偶测温及激光法测温等)难以准确实现炉内温度分布检测，因此，亟须寻求一种精度高、成本低、响应快的方法来实现炉内温度分布测量^[4-5]。

声学层析成像(acoustic tomography，AT)具有可在线测量、测温范围广、非侵入等优点，且适用于大尺度空间检测，是一种有效的温度分布可视化测量方法，具有广阔的发展前景^[6-7]。近年来，很多学者对声学测温进行了相关研究，如：文献[8]对声学传感器阵列进行了优化设计，并通过仿真实验验证了其有效性；文献[9]使用代数重建算法对声波飞行时间矩阵反演，重建了待测区域温度分布；文献[10]提出了一种结合同时代数重建算法与高斯过程回归的重建方法，通过数值仿真验证了算法的有效性与可行性，并进行了实验验证；文献[11]提出了一种基于超声慢度差的反涂抹代数重建算法，获得了较高的重建精度。

AT测量方法的成功应用在一定程度上取决于重建算法的精度，通过适当的算法从声波飞行时间重建出待测温度场分布，其实质是求解一个病态反问题。深度神经网络(deep neural network，DNN)是一种求解病态反问题的有效方法，在很多领域得到了成功应用^[12-13]。本文提出了一种基于DNN的AT温度场重建算法来改善重建质量，采用主成分分析(principal component analysis，PCA)对测量值进行降维处理，构建全连接网络区别峰型，并搭建DNN与BP神经网络预测归一化慢度值及其最值，重建温度场分布。最后，通过数值仿真验证算法的有效性。

1 声学层析测温原理

理想气体条件下，介质温度与声波的传播速度具有如下函数关系：

C = \sqrt[]{(γ \cdot R \cdot T) / M}

(1)

式中：T为介质温度； $γ$ 为气体定压热容与定容热容之比；C为超声波传播速度；R为气体普适常量；M为气体分子质量。

通过在被测区域周围安装收发一体的声波探头对，已知声波传播路径d，通过测量出声波在2个探头对之间的飞行时间t_f，利用声波传播速度C与介质温度T之间的单值函数关系，即可确定该收发器对所在路径的气体介质温度T^[14]：

Z = \sqrt[]{(γ \cdot R) / M}

(2)

t_{f} = \int (1 / C) d l

(3)

T = [d / (t_{f} {\cdot z)]}^{2}

(4)

式中： $γ$ 、R、M为已知量，则可将Z视为常量；l为超声波发射器与接收器之间的路径；当气体环境为空气时，z常取20.05^[15]。

在温度重建过程中，需要对被测区域进行网格离散化^[16-17]。将温度场划分为h个网格，网格内温度值不同，则声波在该区域的传播速度也不同。声波在每一条路径总的传播时间为其在各个小区域内传播时间之和，若预先求出每一条声波路径穿过每个网格的长度W_ij，就可以通过数值计算求出其在每个小网格内的平均速度。假设声波在每个网格内的速度近似相同，则可求出每个网格的温度^[18-19]。用矩阵的形式表达为

[\begin{matrix} w_{11} & \dots & w_{1 h} \\ ⋮ & ⋮ \\ w_{m 1} & \dots & w_{m h} \end{matrix}]

[\begin{matrix} α_{1} \\ ⋮ \\ α_{h} \end{matrix}] = [\begin{matrix} t_{1} \\ ⋮ \\ t_{m} \end{matrix}]

(5)

即

W α = t

(6)

式中：α_i 为第i (i=1, 2,…, h)个网格真实声速的倒数，即慢度；t_k 为第k (k=1, 2,…, m)条超声波路径的渡越时间； W 为距离系数矩阵； α 为声速系数矩阵； t 为超声传播时间系数矩阵。

2 重建方法及原理

2.1 重建方法

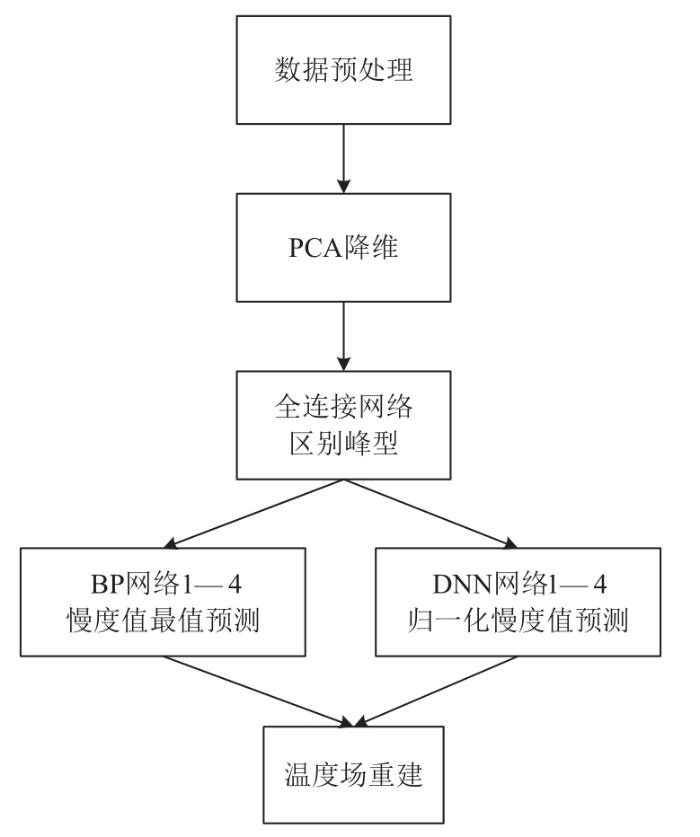
重建算法的步骤如下：对仿真生成的声速传播时间数据进行离差标准化处理，映射到[0,1]区间，将归一化结果经PCA降维处理后，输入全连接网络以区别峰型，分别构建4个DNN网络与BP神经网络对归一化慢度值及其最值进行预测，通过最值将DNN结果反归一化，得到真实慢度值，最后重建温度场。温度场重建流程如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 温度场重建流程图

Fig. 1 Flow chart of temperature field reconstruction

2.2 PCA

原始数据中部分内容价值较低，会影响算法性能，因此需要对测量数据进行降维处理。PCA是一种被广泛使用的数据降维算法，其主要思想是将m维特征映射到n维上，以得到全新的正交特征，即主成分。假设一共有N个样本，给定样本 Q $N \times m$ = ( q₁, q₂,…, q_N )^T，降维后结构为 A_N_×_n，其中n<m，则PCA的数学表达为

A_{N \times n} = Q_{N \times m} B_{m \times n}

(7)

计算平均值：

\bar{q} = \frac{1}{N} \sum_{k = 1}^{N} q_{k}

(8)

计算差值：

e_{k} = q_{k} - \bar{q}

(9)

构建协方差矩阵：

S = \frac{1}{N} \sum_{k = 1}^{N} e_{k} {e_{k}}^{T}

(10)

求解协方差矩阵的特征值和特征向量，选出最大的n个特征值所对应的特征向量，构成主成分分析的解 B $m \times n$ = ( b₁, b₂,…, b_n )。

2.3 全连接网络

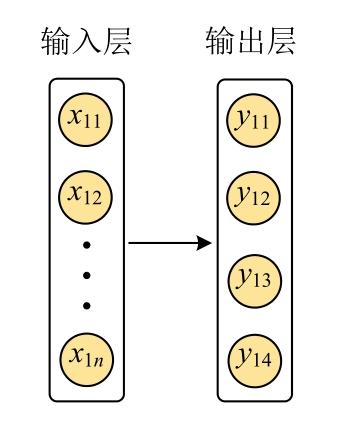
全连接网络相当于一个非线性回归模型，结构简单，没有隐藏层，仅由输入层和输出层构成。本文搭建的全连接网络结构如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 全连接网络结构图

Fig. 2 Structure diagram of fully connected network

输入量 X₁是经PCA降维处理后的 t 值，输出量 Y₁= (y₁₁, y₁₂, y₁₃, y₁₄)表示4种峰型，输出层激活函数为softmax函数。

选用Adam (adaptive moment estimation)优化器训练网络，这种优化算法依靠梯度一阶矩估计与二阶矩估计来动态调整网络参数学习率，与传统算法相比，可使网络参数变化较为平稳。损失函数选择均方误差(mean square error，MSE)函数。

2.4 DNN

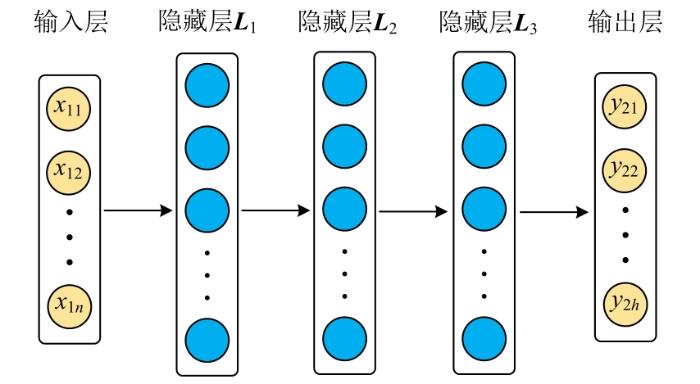
DNN源于早期的人工神经网络，具有更深的网络结构，以及更强的非线性拟合能力、特征提取能力、容错能力、高维度数据处理能力，其由一个输入层、多个隐藏层以及一个输出层构成，每层都含有若干个神经元，不同层神经元之间存在连接权重。本文采用5层DNN对归一化慢度值进行预测，其网络结构如图3所示，其中箭头表示全连接。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 DNN结构图

Fig. 3 Structure diagram of DNN

DNN网络由输入量 X₁到输出量 Y₂的推导过程如下：

隐藏层 L₁、 L₂、 L₃和输出层的输出量分别表示为

L₁=f ( W₁X₁+ b₁)(11)

L₂=f ( W₂L₁+ b₂)(12)

L₃=f ( W₃L₂+ b₃)(13)

Y₂=f ( W₄L₃+ b₄)(14)

式中： b₁、 b₂、 b₃、 b₄为神经元偏置向量； W₁、 W₂、 W₃、 W₄为权重矩阵；f (·)是sigmoid激活函数。DNN网络训练选用Adam优化器，损失函数设置为MSE函数。

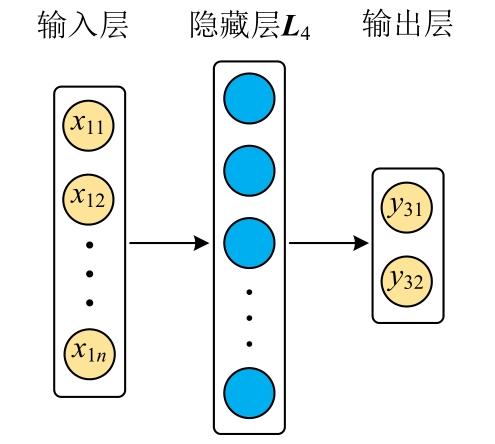
2.5 BP神经网络

BP神经网络是指用BP算法训练的多层前馈神经网络，是应用最广泛的神经网络^[20]。BP算法是一种应用较为广泛的参数学习算法，即误差逆传播算法，其基本思想是梯度下降法，利用梯度搜索技术，使网络的实际输出值和期望输出值的均方误差最小，基本BP算法包括信号的前项传播和误差的反向传播2个过程。BP神经网络由输入层、隐藏层和输出层构成，本文搭建的BP神经网络如图4所示。由输入量 X₁到输出量 Y₃=(y₃₁, y₃₂)的计算过程如下：

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 BP神经网络结构图

Fig. 4 Structure diagram of BP neural network

隐藏层 L₄的输出量为

L₄=f ( W₅X₁+ b₅)(15)

输出层的输出量为

Y₃=f ( W₆L₄+ b₆)(16)

式中： b₅、 b₆是偏置向量； W₅、 W₆是权重矩阵。BP网络优化器与损失函数选择同DNN。

3 数值仿真及分析

通过Matlab R2016b和Python进行数值仿真实验，对4种不同峰型的温度场进行重建，以验证DNN算法的可行性及有效性，并将其与Tikhonov正则化、共轭梯度算法的重建结果进行对比，通过向测量数据添加噪声来验证算法的鲁棒性。

3.1 样本生成

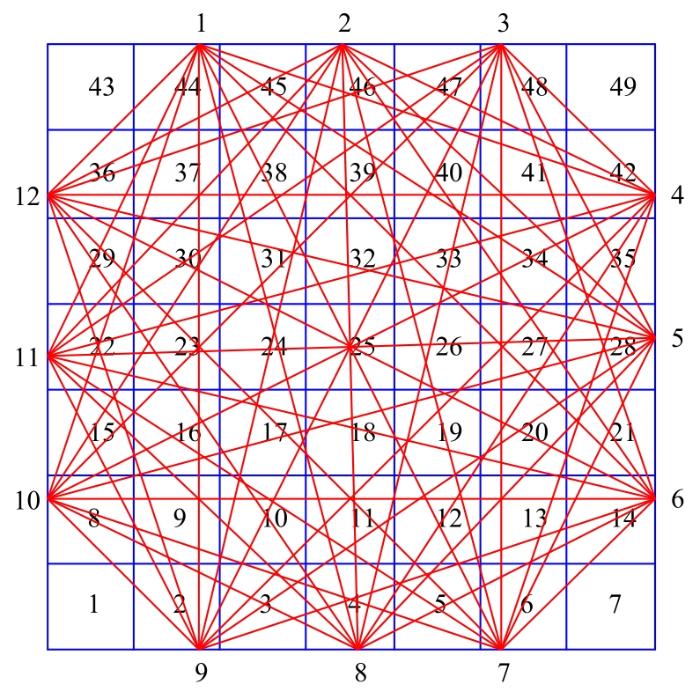
针对10 m×10 m的正方形待测温区域进行仿真实验。一般情况下，温度场重建精度与划分网格数目成正相关，但网格划分数目过多会导致部分网格未被声波传播路径经过，反而会降低重建精度，减缓重建速度。综合考虑，将待测区域划分为7×7的正方形网格，网格划分如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 网格划分示意图

Fig. 5 Schematic diagram of grid division

等距布置12个声波收发器，考虑到收发器在同侧之间不会产生明显的有效信号，因此除去自身及同侧的收发器影响，共形成54条有效声学传播路径。

根据图5所示网格构建单峰、双峰、三峰、四峰4种典型温度分布模型，对于网格中采样点(x, y)处的温度值计算如下：

T_{s} = T_{1} \cdot e^{- a \cdot [(x - x_{1}) + (y - y_{1})]} + 800

(17)

\begin{array}{l} T_{d} = T_{1} \cdot e^{- a \cdot [(x - x_{1}) + (y - y_{1})]} + \\ \begin{matrix} T_{2} \cdot e^{- a \cdot [(x - x_{2}) + (y - y_{2})]} + \end{matrix} 800 \end{array}

(18)

\begin{array}{l} T_{t} = T_{1} \cdot e^{- a \cdot [(x - x_{1}) + (y - y_{1})]]} + \\ \begin{matrix} T_{2} \cdot e^{- a \cdot [(x - x_{2}) + (y - y_{2})]} + \end{matrix} \\ \begin{matrix} T_{3} \cdot e^{- a \cdot [(x - x_{3}) + (y - y_{3})]} + \end{matrix} 800 \end{array}

(19)

\begin{array}{l} T_{f} = T_{1} \cdot e^{- a \cdot [(x - x_{1}) + (y - y_{1})]} + \\ \begin{matrix} T_{2} \cdot e^{- a \cdot [(x - x_{2}) + (y - y_{2})]} + \end{matrix} \\ \begin{matrix} T_{3} \cdot e^{- a \cdot [(x - x_{3}) + (y - y_{3})]} + \end{matrix} \\ \begin{matrix} T_{4} \cdot e^{- a \cdot [(x - x_{4}) + (y - y_{4})]} \end{matrix} + 800 \end{array}

(20)

式中：T₁、T₂、T₃、T₄为600~700的随机数，不同的样本取值不同；a为0.53~0.80的随机数；x₁、y₁，x₂、y₂，x₃、y₃，x₄、y₄反映了峰值位置，不同的样本取值不同，且其值在网格范围内选取。

依据式(17)—(20)随机生成16 600个样本，其中单峰5 000个、双峰2 000个、三峰3 200个、四峰6 400个，选取80%样本作为网络训练集，20%样本作为测试集。

3.2 PCA对网络性能的影响

对训练集归一化 t 值进行PCA降维处理，保留99.9%的贡献率，54维数据被降至50维，保存矩阵 B 并利用其对测试集数据降维。为验证PCA的有效性，分别将PCA处理前后的数据 t 作为峰型判别网络的输入，分析其对网络性能的影响。结果发现：PCA处理前，网络需要训练1 400次才达到稳定，且此时测试集分类准确率仅为94.8%；PCA处理后，网络训练220次即可达到稳定，且测试集分类准确率为100%。

同样将PCA处理前后的数据 t 作为归一化慢度值预测网络的输入，分析PCA对网络性能的影响，其对训练次数的影响如表1所示。

表1 PCA对DNN网络训练次数影响

Tab. 1 Influence of PCA on DNN network training times

峰型	训练次数
峰型	PCA处理后	PCA处理前
单峰	60	100
双峰	140	200
三峰	60	140
四峰	100	200

新窗口打开| 下载CSV

由表1可知，输入数据经PCA处理后，单峰、双峰、三峰、四峰的归一化慢度值预测网络训练次数分别降低了40、60、80、100。可见，数据经PCA处理后可使网络训练更快，还可得到相对更小的损失函数值，使网络模型预测更加准确。

3.3 温度场重建

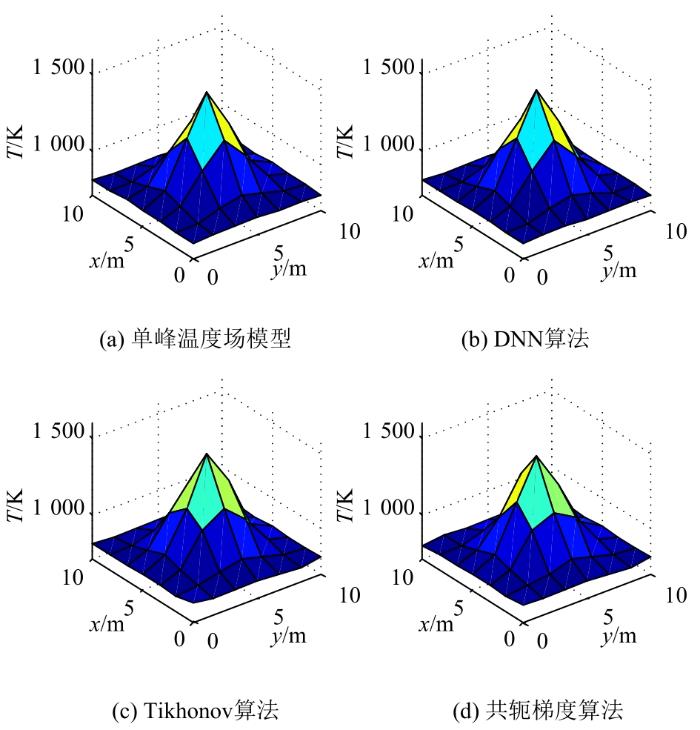
3.3.1 单峰温度场重建

采用DNN算法对单峰温度场模型进行重建，并将Tikhonov正则化算法(正则化参数为0.000_{2)与共轭梯度算法(迭代60次)作为对比，重建结果如图6所示。}

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 单峰温度场重建结果

Fig. 6 Reconstruction results of single peaktemperature field

由图6可以看出，3种算法都可重建出温度场峰型的位置特征，但DNN算法相对于其他2种算法在峰值与温度变化趋势上都有更好的重建精度。为定量评价温度分布重建效果，采用平均相对误差E_ARE及均方根误差E_RMSE作为评价指标，其计算公式分别如下：

E_{A R E} = \frac{1}{h} \sum_{i = 1}^{h} | \frac{\hat{T} (i) - T (i)}{T (i)} |

(21)

E_{R M S E} = \frac{\sqrt[]{\frac{1}{h} \sum_{i = 1}^{h} [\hat{T} (i) - T {(i)]}^{2}}}{T_{m e a n}}

(22)

式中： $\hat{T} (i)$ 为网格中的重建温度值；T(i)为该网格中的模型温度值；T_mean为模型平均温度值。E_ARE、E_RMSE越小，则重建精度越高。

单峰温度场的重建误差如表2所示。由表2可见，DNN算法的重建精度最高，相对于Tikhonov正则化算法，其平均相对误差、均方根误差分别降低了0.37%、1.03%；相对于共轭梯度算法，其平均相对误差、均方根误差分别降低了0.39%、1.33%。

表2 单峰温度场重建误差

Tab. 2 Reconstruction error of single peaktemperature field

重建算法	平均相对误差/%	均方根误差/%
DNN	0.33	0.47
Tikhonov	0.70	1.50
共轭梯度	0.72	1.80

新窗口打开| 下载CSV

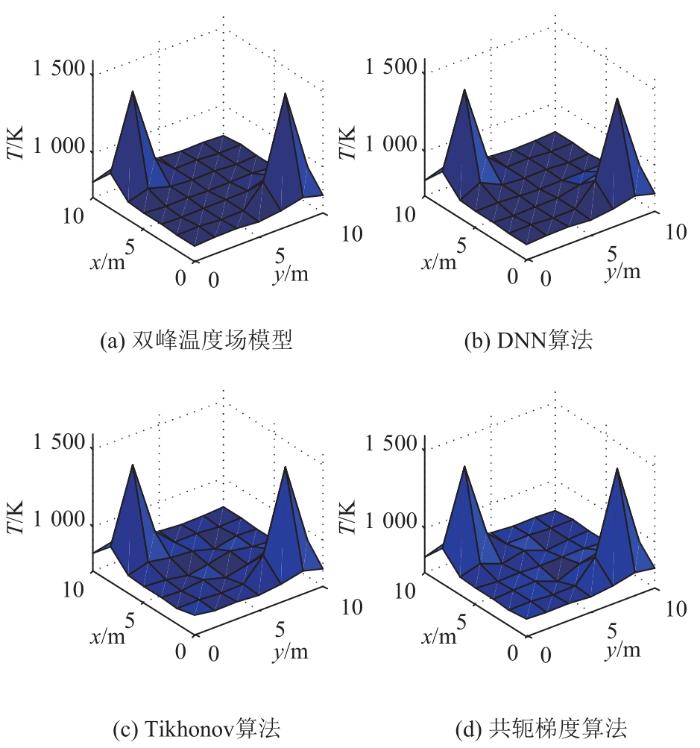
3.3.2 双峰温度场重建

分别采用DNN、Tikhonov正则化及共轭梯度算法对双峰温度场进行重建，2种对比算法参数保持不变，重建结果如图7所示，重建误差如表3所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 双峰温度场重建结果

Fig. 7 Reconstruction results of twin-peaktemperature field

表3 双峰温度场重建误差

Tab. 3 Reconstruction error of twin-peaktemperature field

重建算法	平均相对误差/%	均方根误差/%
DNN	0.36	0.85
Tikhonov	0.62	0.97
共轭梯度	0.59	1.04

新窗口打开| 下载CSV

由表3可见，DNN算法相对于Tikhonov正则化算法，其平均相对误差、均方根误差分别降低了0.26%、0.12%；相对于共轭梯度算法，其平均相对误差、均方根误差分别降低了0.23%、0.19%。这表明DNN算法可以应用于AT重建。

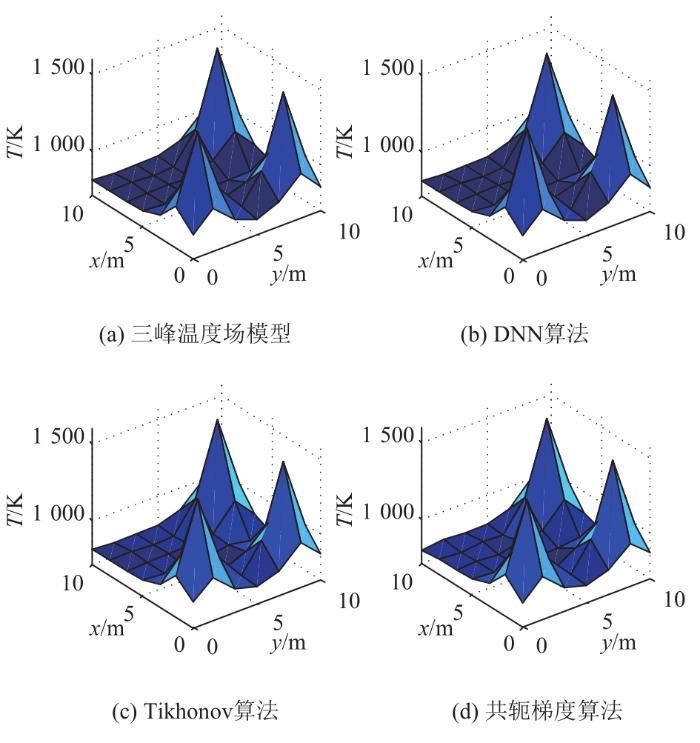
3.3.3 三峰温度场重建

同样采用3种算法对三峰温度场进行重建，观察峰数较多时DNN网络的重建效果。图8为三峰温度场的重建结果，表4为其对应的重建误差。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 三峰温度场重建结果

Fig. 8 Reconstruction results of three-peaktemperature field

表4 三峰温度场重建误差

Tab. 4 Reconstruction error of three-peaktemperature field

重建算法	平均相对误差/%	均方根误差/%
DNN	0.31	0.67
Tikhonov	0.62	0.94
共轭梯度	0.51	0.86

新窗口打开| 下载CSV

由表4可见，DNN算法相对于Tikhonov正则化算法，其平均相对误差、均方根误差分别降低了0.31%、0.27%；相对于共轭梯度算法，其平均相对误差、均方根误差分别降低了0.20%、0.19%。这表明峰数较多时，DNN算法仍能保持较高的重建精度。

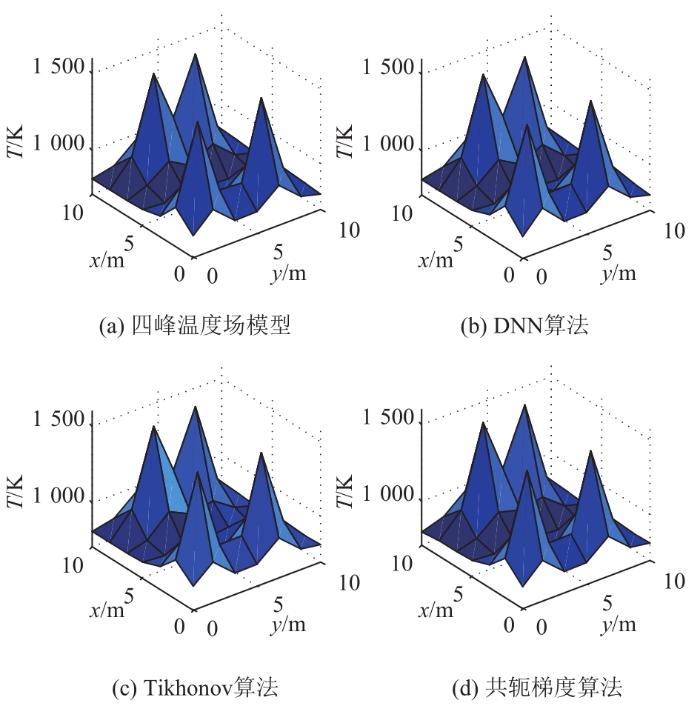
3.3.4 四峰温度场重建

进一步增加峰数，采用3种算法对四峰温度场进行重建，其重建结果如图9所示，重建误差如表5所示。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 四峰温度场重建结果

Fig. 9 Reconstruction results of four-peaktemperature field

表5 四峰温度场重建误差

Tab. 5 Reconstruction error of four-peaktemperature field

重建算法	平均相对误差/%	均方根误差/%
DNN	0.36	0.62
Tikhonov	0.64	0.98
共轭梯度	0.50	0.89

新窗口打开| 下载CSV

由表5可见，DNN算法相对于Tikhonov正则化算法，其平均相对误差、均方根误差分别降低了0.28%、0.36%；相对于共轭梯度算法，其平均相对误差、均方根误差分别降低了0.14%、0.27%。在多峰情况下DNN算法的重建精度仍能优于传统的重建算法，这充分验证了本文方法的有效性。

另外，通过对比3种算法的运行时间可知，DNN、Tikhonov正则化及共轭梯度算法的平均重建时间分别为0.015、0.013、0.016 s，其重建耗时仍在同一数量级上，并无显著区别。

3.4 抗噪性验证

通过对声波飞行时间测量值 t 添加噪声，测试算法的抗噪性能，将噪声等级 $η$ 定义为：

η = \frac{‖t - t_{o}‖}{‖t‖} \times 100 %

(23)

t_{o} = t + λ σ

(24)

式中： t_o 为添加噪声后的声波飞行时间数据； $λ$ 为系数； $σ$ 为满足均值为0、标准差为1的正态分布随机数矩阵。

噪声水平设置为0.5%，采用DNN、Tikhonov正则化及共轭梯度算法分别对图6—9的4种温度场进行重建，其平均相对误差如图10所示。

图10

新窗口打开| 下载原图ZIP| 生成PPT

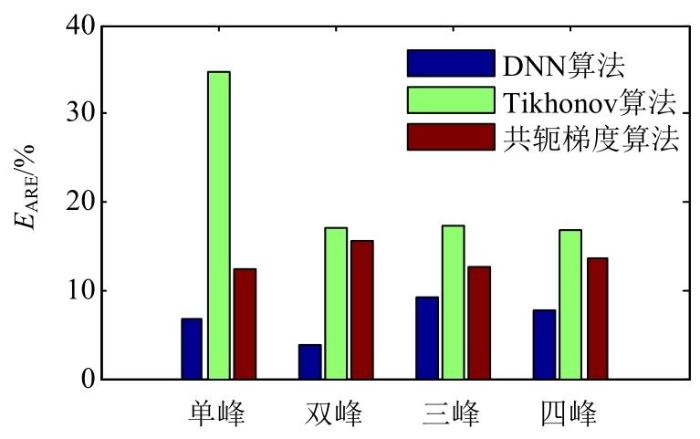
图10 噪声水平为0.5%时温度分布重建平均相对误差

Fig. 10 Average relative error of temperature distribution reconstruction when the noise level is 0.5%

由图10可见，在测量数据噪声水平为0.5%时，DNN算法重建结果的平均相对误差最小，共轭梯度算法次之，Tikhonov算法的平均相对误差最大，表明DNN算法具有较好的鲁棒性。

4 结论

1）多种火电厂锅炉炉膛温度场分布模型的仿真结果表明，DNN算法的重建质量优于Tikhonov正则化算法与共轭梯度算法，证实了DNN算法在炉膛温度分布重建上的可行性与有效性。

2）对于不含噪声的测量数据，DNN算法重建结果平均相对误差、均方根误差分别小于0.36%和0.85%，可以有效重建待测区域温度场分布。

3）当测量数据噪声等级为0.5%时，DNN算法对4种炉膛温度场模型重建结果的平均相对误差均小于Tikhonov正则化算法与共轭梯度算法，表现出良好的鲁棒性。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

刘厦，刘石，任婷．

基于SA-ELM的声学层析成像温度分布重建算法

[J]．化工学报，2017，68(6)：2434-2446． doi:10.11949/j.issn.0438-1157.20161597