基于数据驱动的NO x 稳定性评价

doi:10.12096/j.2096-4528.pgt.21139

基于数据驱动的NO _x 稳定性评价

彭家琪¹, 肖海平¹, 董竹雨¹, 孙保民¹, 白翎², 孙志春²

1.华北电力大学能源动力与机械工程学院, 北京市昌平区 102206

2.北京国电电力有限公司, 北京市朝阳区 100176

Data-driven NO _x Stability Evaluation

PENG Jiaqi¹, XIAO Haiping¹, DONG Zhuyu¹, SUN Baomin¹, BAI Ling², SUN Zhichun²

1.School of Energy, Power and Mechanical Engineering, North China Electric Power University, Changping District, Beijing 102206, China

2.Beijing Guodian Power Corporation, Chaoyang District, Beijing 100176, China

收稿日期: 2022-04-27

基金资助:

国家重点研发计划项目. 2018YFB060420103

Received: 2022-04-27

作者简介 About authors

彭家琪(1998)，男，硕士研究生，主要从事电力大数据研究，st_pengjiaqi@126.com；

肖海平(1978)，男，博士，副教授，主要从事基于大数据的锅炉设备优化、脱硫脱硝系统优化等方面的研究，本文通信作者，xiaohaiping@ncepu.edu.cn；

孙志春(1974)，男，博士，教授级高级工程师，主要从事发电企业安全生产管理方面的工作，16010068@chnenergy.com.cn。

摘要

燃煤机组烟气NO _x 浓度的稳定性影响脱硝系统的运行性能。通过构建稳定性评估模型，实现对NO _x 浓度大数据分布的量化评价。构建了K均值聚类与3σ准则相结合的原始大数据清洗方法，通过滑动窗格法划分不同工况数据。基于最小二乘回归，建立了NO _x 浓度基准值模型。基于偏离程度，构建了偏离度函数和稳定系数函数，归一化处理后得到稳定性评分函数，从而实现全负荷NO _x 稳定性定量评价。利用该模型对某660 MW燃煤机组NO _x 数据进行评估，结果表明：NO _x 浓度分布整体集中度高，与负荷率呈正相关，变负荷工况稳定性得分比稳定工况低2.35%左右；将负荷率从50%提升至100%，稳定性得分提升了21.28%，说明所构建的模型能有效评价NO _x 分布的稳定性，为机组对标评价提供了依据。

关键词： 燃煤机组 ; NO _x 稳定性 ; 数据清洗 ; 最小二乘回归 ; 稳态检测

Abstract

The stability of NO _x concentration in a coal-fired unit affects the operation performance of denitrification system. By constructing the stability evaluation model, the quantitative evaluation of the big data distribution of NO _x concentration was realized. The original big data cleaning method combining K-means clustering and 3σ criterion was constructed, and the data of different working conditions were divided by the sliding window method. A NO _x concentration reference value model was established based on the least-squares regression method. Based on the deviation degree, the deviation degree function and the stability coefficient function were constructed, and the stability scoring function was obtained after normalization, so as to realize the quantitative evaluation of the stability of full load NO _x . The model was used to evaluate NO _x data from a 660 MW coal-fired unit. The results show that the overall concentration of NO _x concentration distribution is high and positively correlated with load rate. The stability score of variable load condition is about 2.35% lower than that of stable condition. When the load rate is increased from 50% to 100%, the stability score is increased by 21.28%. It shows that the model can effectively evaluate the stability of NO _x_{distribution and provide a basis for benchmarking coal-fired units.}

Keywords： coal-fired unit ; NO _x stability ; data cleaning ; least-squares regression ; steady state detection

PDF (6423KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

彭家琪, 肖海平, 董竹雨, 孙保民, 白翎, 孙志春. 基于数据驱动的NO _x 稳定性评价. 发电技术[J], 2023, 44(2): 163-170 DOI:10.12096/j.2096-4528.pgt.21139

PENG Jiaqi, XIAO Haiping, DONG Zhuyu, SUN Baomin, BAI Ling, SUN Zhichun. Data-driven NO _x Stability Evaluation. Power Generation Technology[J], 2023, 44(2): 163-170 DOI:10.12096/j.2096-4528.pgt.21139

0 引言

燃煤过程中生成的NO _x 严重污染大气环境，燃煤机组普遍使用选择性催化还原(selective catalytic reduction，SCR)高效脱除烟气NO _x^[1]。由于浓度场不均匀、工况波动频繁等因素，SCR入口NO _x 浓度稳定性差，造成氨逃逸概率提高^[2-3]。逃逸的氨气与烟气中三氧化硫反应生成硫酸氢铵，使下游设备堵塞、沾污、腐蚀问题加剧。因此，评价SCR入口NO _x 浓度分布稳定性，有利于指导机组低NO _x 燃烧运行优化和高效实施精准喷氨，对电力生产具有重要意义。

针对SCR入口NO _x 浓度分布稳定性差的问题，许多学者进行了研究。文献[4-6]基于仿真软件，模拟了喷嘴、混合器等系统设备对流场均匀性的影响。文献[7-9]则引入神经网络算法、遗传算法等机器学习方法，建立了NO _x 浓度预测模型并分析了NO _x 浓度分布。然而，目前研究缺少NO _x 浓度分布稳定性评价指标与模型，无法定量评价NO _x 浓度的波动特性。

通过建立机组评价模型、量化机组性能指标，有利于推进系统优化，增加机组竞争力。当前研究主要集中在机组经济性^[10-12]、安全性^[13-14]、环保性^[15-16]评价方面，评价指标采用数据集的标准差、相关系数、熵值等进行构造。部分研究者^[17-21]则使用层次分析法、模糊评价法等综合评价方法对机组进行总体评价。这些研究应用数学模型量化机组性能指标，用数学语言表述机组关键参数变化趋势，并反映机组对关键参数的控制质量。

借鉴上述机组评价指标构造方法，本文基于最小二乘回归，建立NO _x 稳定性评价模型，按不同工况定量评价NO _x 稳定性，为脱硝系统优化控制提供数据支持。

1 稳定性评价模型

1.1 预处理环节

1.1.1 NO _x 浓度折算

根据大气污染物排放标准^[22]，实测得到的火电厂烟尘、二氧化硫、氮氧化物等大气污染物排放质量浓度必须折算为基准氧含量下的污染物排放质量浓度，即

ρ = ρ^{'} \times \frac{21 - φ (O_{2})}{21 - φ^{'} (O_{2})}

(1)

式中： $ρ$ 为在基准氧含量下的大气污染物排放质量浓度，mg/m³； $ρ^{'}$ 为实测大气污染物排放质量浓度，mg/m³； $φ^{'} (O_{2})$ 为实测氧体积分数，%； $φ (O_{2})$ 为基准氧体积分数，%。对于燃煤锅炉，基准氧体积分数为6%。

1.1.2 数据清洗

根据数据特点，主要处理原始数据中的离散值。离散值也称逸出值，与其他数据相比，通常差异较大。离散值处理方法主要包括统计分布法(如拉依达准则(3σ准则^[23])、格拉布斯准则)和自学习方法(如聚类算法、回归算法)。

其中，由于3σ准则计算简单，被广泛应用于异常值剔除。准则内容如下：对于正态分布的数据对象，样本某一数据 $x_{i}$ 与样本均值 $\bar{x}$ 的残差要小于3倍样本标准差σ，该数据才能通过检测，即满足

ν_{i} = |x_{i} - \bar{x}| < 3 σ

(2)

对于SCR入口NO _x 浓度数据，数据集正态性较差，无法直接使用3σ准则。因此，需先对原始样本集按不同负荷水平进行分类，之后分别对每一簇数据使用3σ准则。

本文选取K均值聚类算法对样本集进行分类。K均值聚类算法采用迭代求解方式，随机选取K个初始聚类中心，计算每个样本与初始聚类中心的距离(一般指欧式距离)，将各样本划归最近的聚类中心所属类别，每一类样本的均值将作为新的聚类中心。通过反复迭代，直至满足收敛条件，最终实现数据分类。

对于数据处理结果，本文采用变异系数反映清洗前后的数据离散情况。变异系数C_V表示为

C_{V} = σ / μ

(3)

式中μ为样本的均值。变异系数越小，则数据的离散程度越小。

1.1.3 稳态检测

对于燃煤机组，关键参数在稳定负荷与变负荷下运行规律不同。因此，只有通过稳态检测区分稳态与过渡态数据，才能有效分析系统稳定性。

本文中采用普适性较强的滑动窗格法^[24]对数据进行稳态检测。对于时间序列连续的数据集，按需设定窗口大小与标准差阈值R。沿着时间序列滑动窗口，求取窗口内数据的标准差S_t，若满足条件

S_{t} < |R \times M|

(4)

则表示窗口内数据段处于稳定状态。式中M表示窗口内数据的平均值。

本文将采取“试凑法”设定窗口大小与标准差阈值，即先取一段典型稳定负荷数据，把这段数据的标准差作为初始标杆，之后不断调整，直至标准差阈值R能够区分稳定阶段与变负荷阶段的节点。

1.1.4 数据预处理结果

1）数据清洗情况

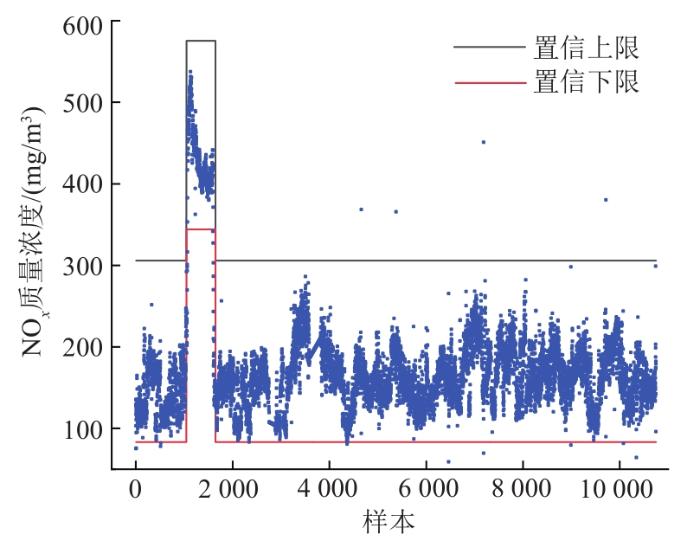
图1为部分NO _x 浓度数据的清洗效果。采用K均值聚类与3σ准则相结合的数据清洗方法确定置信区间，剔除坏值。NO _x 浓度密集区域反映NO _x 浓度随时间变化的大致趋势，偏离密集区域较大的离散点即为异常值。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 数据清洗结果

Fig. 1 Data cleaning results

经折算后，NO _x 浓度数据被K均值聚类算法分为2簇，分别计算2个区间内数据的置信区间，置信上、下限如图1所示。2条折线段之外的数据即被准则判定为粗大误差，予以剔除。由此可见，置信区间能够显著区分密集区域与离散点，实现异常值剔除。

2簇数据集经清洗后，数据剔除率均不足0.6%，但变异系数下降率却超过1.74%，说明剔除的是偏离程度较高的离散值，清洗效果明显。

结合K均值聚类与3σ准则，剔除了明显偏离置信区域的数据，提高了数据质量，并使3σ准则适用于负荷频繁波动的工况。

2）稳态检测结果

代入某660 MW燃煤机组数据，以某段典型工况下标准差为标杆，不断增加阈值，直至稳态与过渡态间的节点能被明显识别，最终确定窗口大小为10，标准差阈值R=3。再基于变负荷速率，分离升降负荷过程的数据。其中，稳定负荷数据约占总体的89.19%，升负荷过程占比4.53%，降负荷过程占比6.28%。

1.2 稳定性评价方法

1.2.1 稳定系数模型

目前，数据稳定性评价方法主要有极差法、方差法、偏差程度法、假设检验p值法、变异系数法和信息熵法。大部分方法基于数据集的方差、均值计算数据稳定性，一部分方法根据样本概率密度计算数据稳定性。

借鉴偏差程度^[25]思想，定义数据偏离度δ为

δ = \frac{x_{i} - x_{o}}{x_{o}} \times 100 %

(5)

式中： $x_{i}$ 为在工况i下的测量值； $x_{o}$ 为在相同工况下的标准值。

基于偏离度定义稳定系数S，对某一阶段内数据稳定性进行量化计算：

S = \frac{\sum_{i = 1}^{n} |δ_{i}|}{n}

(6)

式中： $δ_{i}$ 为在工况i下的数据偏离度； $n$ 为该阶段内的样本数量。

稳定系数S为无量纲数，且S ≥0。S越小，表示该阶段内数据越接近标准值，运行越稳定。当NO _x 浓度处于理想稳定状态时，稳定系数S =0。

基于稳定系数S，采用归一化方法定义稳定性得分G，折算为百分制：

G = \frac{100}{S_{L} - S_{H}} (S - S_{H})

(7)

式中： $S_{H}$ 为稳定系数上限； $S_{L}$ 为稳定系数下限。

只需确定稳定系数上、下限，即可将稳定性得分G变成稳定系数S的单值函数。

除了采用稳定系数S与稳定性得分G外，本文还采用直方图以及概率密度曲线直观地反映NO _x 偏离度δ的分布情况。直方图是用一系列宽度相等、高度不等的长方形柱体来表示数据分布特征的图形，其宽度代表组距，高度代表指定组距内数据的频数。概率密度函数f (x)是累计分布函数F(x)的导数，满足

F (x) = \int_{- \infty}^{t} f (t) d t

(8)

则偏离度δ概率密度曲线上的点表示偏离度δ在某个值附近的可能性，同样可以展现偏离度δ分布情况。

通过概率密度曲线了解偏离度δ的变化趋势，通过直方图则可以直接反映偏离度δ在某个区间内的频率。

1.2.2 基准值模型

本文将基于最小二乘回归算法，拟合求解NO _x 浓度随负荷变化的基准值曲线。最小二乘法基本原理如下：

对于给定数据集

D = {(x_{1}, y_{1}), (x_{2}, y_{2}), \dots, (x_{m}, y_{m})}

(9)

回归模型满足：

f (x_{i}) = w X (x_{i}) + b

(10)

并使 $f (x_{i})$ 趋向于 $y_{i}$ ，即误差最小化。式中： w 为待求解的权重矩阵； $X (x_{i})$ 为自变量矩阵；b为偏置系数。

其中，以欧式距离为误差标准，基于均方误差最小化的求解模型为最小二乘法。则回归问题可简化为由函数组 $φ = s p a n {φ_{0} (x), φ_{1} (x), \dots, φ_{n} (x)}$ 构造的目标函数：

S (x_{i}) = \sum_{j = 0}^{n} α_{j} φ_{j} (x_{i})

(11)

对于m组数据，需满足误差 $δ_{i} = S^{*} (x_{i}) - y_{i}$ 平方和最小化：

{‖δ‖}_{2}^{2} = \sum_{i = 0}^{m} δ_{i}^{2} = \sum_{i = 0}^{m} [S^{*} (x_{i}) - y_{i}]^{2} = m i n \sum_{i = 0}^{m} [S (x_{i}) - y_{i}]^{2}

(12)

函数组 $φ$ 线性无关，根据数据变化的特点确定。但拟合数据往往是离散的，无法确定数据变化的特点。普遍采用多项式 $φ = s p a n {1, x, \dots, x^{n}}$ ，满足哈尔条件，方程存在唯一解。

对于稳定性计算模型，基准值曲线的物理意义为：某一负荷x_i 处附近，NO _x 浓度测量值y出现频率最高位置在拟合值S(x_i )附近。这并不代表机组在负荷等于x_i 处的标准NO _x 浓度等于拟合值S(x_i )。但在拟合值S(x_i )附近，最有可能实现NO _x 浓度的高稳定性。

同时，将拟合函数看作NO _x 浓度随负荷变化的基准值曲线，可以减弱煤种变化、设备状态变化等因素产生的影响，具有较强的普适性，并且可以削弱离散点的影响，提高预测准确性。

2 NO _x 浓度分布稳定性评价

2.1 NO _x 浓度偏离度全负荷分布情况

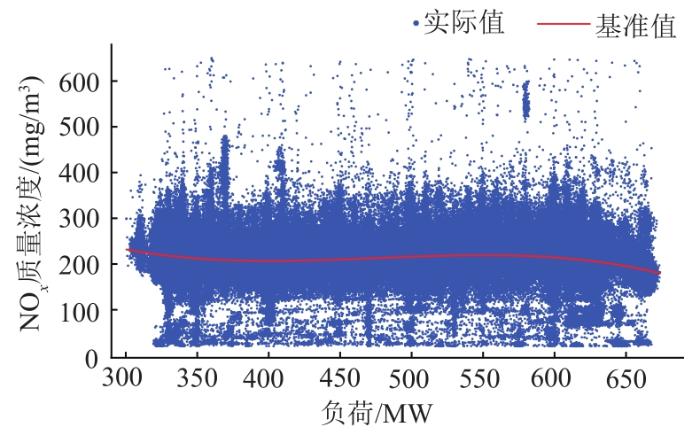
本文对50万条原始数据进行预处理，如图2所示，NO _x 质量浓度实际值在100~350 mg/m³(标准状态下)内分布最密集，在其他区域NO _x 浓度基本呈离散分布。选用最高次幂为3的多项式作为目标函数基底，基于最小二乘法构建NO _x 浓度分布稳定性计算模型。基准值曲线表达式为

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 NO _x 浓度实际值与基准值对比

Fig. 2 Comparison of the actual value of NO _x concentration with the reference value

f (x) = - 7.6 \times 10^{- 6} x^{3} + 0.01 x^{2} - 5.04 x + 937.48

(13)

从图2可以看出，NO _x 基准值随着负荷的增加而缓慢下降，整体平稳，当从50%负荷升至100%负荷时，NO _x 基准值仅下降了11.70%。低负荷时，出于稳燃目的，烟气含氧量较高，NO _x 浓度基准值较高。随着负荷增加，烟气含氧量下降，NO _x 浓度基准值也随之下降。

但实际值数据量过大，基准值曲线附近出现数据堆叠，掩盖了部分工况下的数据特征。为有效分析系统稳定性，本文将全负荷拆分为稳定负荷阶段、升负荷阶段与降负荷阶段，分段进行分析，具有针对性。不同工况下NO _x 浓度偏离度分布如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

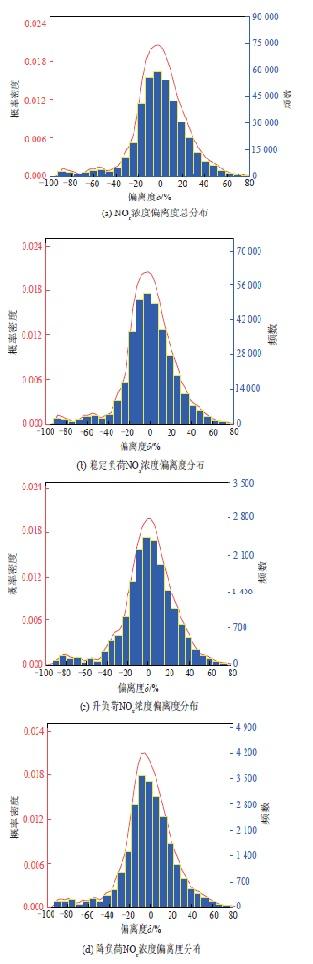
图3 不同工况下NO _x 浓度偏离度分布

Fig. 3 Distribution of NO _x concentration deviation under different working conditions

在全负荷下，NO _x 浓度偏离度δ概率密度曲线类似于正态分布曲线，偏离度δ关于中轴线呈对称分布。经过稳态检测后，3种工况下NO _x 浓度偏离度δ概率密度曲线与直方图高度相似。概率密度曲线峰值均在0.020左右，且在偏离度-80%附近皆存在小波峰。结果表明，在海量数据样本下，稳定负荷与升、降负荷下的NO _x 浓度分布具有相似规律，本模型能够准确评价全负荷下NO _x 浓度分布的稳定性。

根据质量控制原则，当生产过程满足产品质量时，样本规格的残差会被控制在3σ以内。如表1所示，稳态负荷数据集中度高于变负荷过程，但NO _x 浓度偏离度δ占比差距均不到2.0%，与变负荷过程具有相同的偏离度δ分布规律。

表1 NO _x 浓度偏离度在不同区间内占比

Tab. 1 NO _x concentration deviation proportion in different intervals

工况	区间占比/%
工况	$\|δ\| < σ$	$\|δ\| < 2 σ$	$\|δ\| < 3 σ$
全负荷	78.34	94.10	98.29
稳负荷	78.49	94.10	98.29
升负荷	76.73	94.39	98.59
降负荷	77.33	93.67	98.14

新窗口打开| 下载CSV

由表1可见，各工况下NO _x 浓度偏离度δ在3σ内占比均高于98%，数据集中度高，NO _x 稳定性好，说明本模型能准确评价全负荷下NO _x 浓度分布的稳定性。

2.2 稳定负荷中典型工况分析

为提高对脱硝系统的管理能力，需对机组负荷进行更精细的划分，便于机组对标评价。因此需针对机组特点，分离并分析几个典型工况。本文选取了100%稳定负荷、70%稳定负荷、50%稳定负荷3段样本进行分析，结果如图4和表2所示。可以看出，随着负荷率增大，概率密度曲线峰值逐渐增加，到100%负荷时峰值达到0.028；随着负荷升高，两侧直方柱体也会向中心集中，说明NO _x 浓度分布更加集中，稳定性增强。

图4

新窗口打开| 下载原图ZIP| 生成PPT

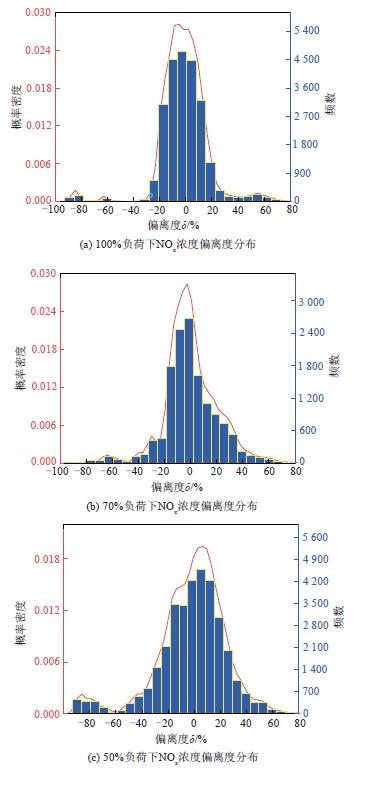
图4 不同负荷稳定工况下NO _x 浓度偏离度分布

Fig. 4 Distribution of NO _x concentration deviation in stable conditions under different loads

表2 3种典型工况下NO _x 浓度偏离度分布

Tab. 2 Distribution of NO _x concentration deviation under three typical working conditions

工况	区间占比/%
工况	$\|δ\| < σ$	$\|δ\| < 2 σ$	$\|δ\| < 3 σ$
100%负荷	88.23	96.46	98.51
70%负荷	78.47	95.34	99.10
50%负荷	77.84	94.44	97.52

新窗口打开| 下载CSV

由表2可以看出，在不同负荷率下 $|δ| < 3 σ$ 的比例均高于97%，数据集中度较高，且NO _x 浓度数据集中度与负荷率呈正相关，稳定性也随着负荷的增加而增强。尤其是在100%负荷下， $|δ| < σ$ 的比例要明显高于其他工况，NO _x 分布稳定性最好，说明本模型能够准确评价不同负荷率下NO _x 浓度分布的稳定性。

2.3 NO _x 浓度分布稳定性对标评价

基于燃煤机组对标评价需求，在某660 MW燃煤机组应用所建模型，将NO _x 浓度稳定性转化为无量纲分数，结果如表3、4所示。

表3 不同工况下NO _x 稳定性分数

Tab. 3 NO _x stability grade under different working conditions

工况	全负荷	稳负荷	升负荷	降负荷
得分	89.00	89.09	87.80	88.68

新窗口打开| 下载CSV

表4 不同负荷率稳负荷下NO _x 稳定性分数

Tab. 4 NO _x stability grade under steady load at different load rates

负荷率/%	100	70	50
得分	98.78	94.03	87.50

新窗口打开| 下载CSV

机组不同状态下呈现NO _x 分布规律基本一致，变负荷工况下稳定性分数G仅比稳定工况下低2.35%左右。但负荷对NO _x 稳定性影响较大，且NO _x 稳定性会随着负荷的升高而增强。在50%负荷下，稳定性分数G仅为87.50，甚至低于机组平均水平，但升至100%负荷时稳定性分数G提升了21.28%，说明稳定性分数模型能够有效分析不同工况下NO _x 浓度分布稳定性变化规律。

3 结论

1）构建了K均值聚类与3σ准则相结合的数据清洗方法，能够有效剔除异常值，适用于机组运行全负荷工况。

2）通过滑动窗格法实现不同机组状态的数据分离，有利于对不同机组状态下NO _x 浓度稳定性的精准分析。

3）基于最小二乘回归算法和物理偏离度，构建了NO _x 浓度基准值模型和稳定系数函数，耦合形成稳定性评分函数，实现了机组全负荷NO _x 稳定性评价。该模型有利于量化NO _x 浓度工程控制质量，为脱硝系统优化控制提供数据支持。

4）应用模型分析某660 MW机组数据，全负荷范围内NO _x 浓度偏离度δ在3σ内占比均高于98%，整体稳定性强；NO _x 浓度分布规律高度相似，均类似于正态分布；随着负荷升高，NO _x 浓度分布集中度明显提高；变负荷工况下稳定性得分比稳定工况下低2.35%左右；当负荷率从50%升至100%时，稳定性得分提升了21.28%。由此说明，本模型能够准确评价不同工况下NO _x 浓度分布稳定性。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

黄权浩，赵光耀，兰艳旭，等．

脱硝系统流场优化在330 MW机组上的实践

[J]．浙江电力，2021，40(8)：102-106．