基于双层规划的碳减排配煤优化方法研究

doi:10.12096/j.2096-4528.pgt.22012

基于双层规划的碳减排配煤优化方法研究

陈思勤¹, 朱伊囡², 李晓辰¹, 王学海¹

1.华能国际电力股份有限公司上海石洞口第二电厂, 上海市宝山区 200942

2.上海电力大学自动化工程学院, 上海市浦东新区 201306

Research on Optimization Method of Coal Blending for Carbon Emission Reduction Based on Bi-level Programming

CHEN Siqin¹, ZHU Yinan², LI Xiaochen¹, WANG Xuehai¹

1.Shanghai Shidongkou Second Power Plant, Huaneng Power International, Inc. , Baoshan District, Shanghai 200942, China

2.School of Automation Engineering, Shanghai University of Electric Power, Pudong New District, Shanghai 201306, China

收稿日期: 2022-05-20

基金资助:

上海市“科技创新行动计划”高新技术领域资助项目.  19511101600
上海市科学技术委员会工程技术研究中心资助项目.  14DZ2251100
中国华能集团有限公司2020年度科技项目.  HNKJ-F2002

Received: 2022-05-20

作者简介 About authors

陈思勤(1970)，女，硕士，正高级工程师，主要从事电厂生产过程自动化和智能化研究工作，chensiqin36881@hotmil.com；

朱伊囡(1998)，女，硕士研究生，从事火电厂配煤掺烧技术研究工作，zyn1998921@163.com；

李晓辰(1985)，男，高级工程师，从事电厂运行管理研究工作；

王学海(1985)，男，硕士，工程师，从事电厂运行管理研究工作。

摘要

随着“双碳”目标升级为国家战略，煤电作为发电行业减碳的重中之重，燃煤电厂在碳排放量的限制上面临巨大的考验。运用双层规划的方法，考虑政府管理部门碳排放配额与电厂配煤掺烧相结合，建立了火电机组低碳配煤优化模型，模型上层为政府管理部门目标，追求既定碳排放总量下电厂减排成本最小化；下层为电厂部门目标，追求配煤成本和碳排放成本最小化。采用混沌粒子群优化(chaotic particle swarm optimization，CPSO)算法求解该模型，计算结果为政府管理部门碳排放配额分配和电厂运行人员煤炭掺配提供一定参考，具有较好的应用价值与指导作用。

关键词： 碳排放配额 ; 双层规划模型 ; 配煤优化 ; 混沌粒子群优化(CPSO)算法

Abstract

As the “dual carbon” goal has been upgraded to a national strategy, coal-fired power plants are the top priority for carbon reduction in the power generation industry, and coal-fired power plants are facing a huge challenge in limiting carbon emissions. Using the method of bi-level programming model, this paper established a low-carbon coal blending optimization model for thermal power units by considering the combination of carbon emission quotas for regulatory agencies and coal blending in power plants. The upper layer is the goal of the government management department, which seeks to minimize the cost of emission reduction of power plants under the given total carbon emissions. The lower layer is the goal of the power plant sector, pursuing the minimization of coal blending cost and carbon emission cost. The chaotic particle swarm optimization (CPSO) algorithm was used to solve the model. The calculation provides a certain reference for the allocation of carbon emission quotas for regulatory agencies and coal blending for power plant operators, and has good application value and guiding role.

Keywords： carbon emission quota ; bi-level programming model ; coal blending optimization ; chaotic particle swarm optimization (CPSO) algorithm

PDF (1489KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

陈思勤, 朱伊囡, 李晓辰, 王学海. 基于双层规划的碳减排配煤优化方法研究. 发电技术[J], 2023, 44(2): 155-162 DOI:10.12096/j.2096-4528.pgt.22012

CHEN Siqin, ZHU Yinan, LI Xiaochen, WANG Xuehai. Research on Optimization Method of Coal Blending for Carbon Emission Reduction Based on Bi-level Programming. Power Generation Technology[J], 2023, 44(2): 155-162 DOI:10.12096/j.2096-4528.pgt.22012

0 引言

“碳达峰、碳中和”目标的落实将对燃煤发电行业产生深刻影响，而电煤作为连接煤炭、电力两大能源行业的纽带，将受到更为深远的影响^[1-5]。目前我国已经成为全球第一大温室气体排放国，而我国的能源结构决定了燃煤发电是我国排放CO₂主要污染源之一。随着电力需求的不断增加，煤炭消耗量也会越来越多，煤炭的燃烧进一步加剧了燃煤电厂排放的环境污染，在“双碳”政策的压力下，燃煤电厂的碳减排行动迫在眉睫。

配煤掺烧，即对多种煤种进行混配，以确保挥发分、发热量、灰分、硫含量和水分满足发电用煤的需求，已被证明可以有效控制污染排放。然而，想要配煤达到锅炉燃烧需求，必须克服2个主要障碍。第一个障碍是需要保证混煤特性在燃烧特性的目标范围内。Wu等人^[6]采用专家控制策略来计算不同煤种配比，结合了神经网络、数学模型和规则模型方法，确保配煤后煤种特性在目标范围内；黄海东等人^[7]以混煤与锅炉目标煤的煤质偏差作为目标函数，调节混煤成分与目标煤的接近程度，实现配煤优化；夏季等人^[8]运用模糊数学的方法建立了适用于电站锅炉的基于正交遗传算法的智能配煤模型。第2个障碍是从经济性、环保性和安全性等多角度出发，确定最佳配煤比，因此需要进行多目标寻优。Shih等人^[9]通过煤炭成本、配煤成本、硫排放成本和硫排放标准差建立多目标机会约束优化模型，以优化排放性能来降低配煤成本。王英敏等人^[10]采用K均值聚类算法和专家规则对进厂煤种进行智能储煤，采用多目标优化方法对制粉系统进行优化管理，得到合理配煤比例，使混煤掺烧达到安全、经济和环保的作用，并设计掺烧收益模块，进行经济性分析。张宇等人^[11]基于污染物的生成、排污罚款和污染物控制设备等因素，采用支持向量机建立了锅炉污染物生成预测模型，并以最低运行成本为目标，对配煤模型进行优化，从而减少了减排费用、氨耗成本、脱硫脱硝等成本。

以往对配煤优化的研究只考虑了单一的决策者问题，也就是说，电厂是唯一考虑的决策者。然而，在实际运营中，考虑降低环境污染的计划时，往往有多个利益相关者，特别是政府管理部门与电厂之间有相互冲突的目标。例如，地方当局最关心的是环境污染排放问题，而电厂则希望追求更高的收益。LÜ等人^[12]采用平衡策略的配煤方法，能够减少多种污染物排放的同时达到不同利益者之间的权衡。

因此，本文将双层规划模型融入配煤方法中，在低碳约束下，既做到政府管理部门基于碳排放配额目标下追求的减排成本最小化，也做到电厂部门配煤综合成本最小化，寻找两者之间的最佳平衡点，并引入混沌粒子群优化(chaotic particle swarm optimization，CPSO)算法求解该双层规划模型，辅助运行管理人员做出最优配煤决策方案，智能化地指导电厂进行精准化配煤掺烧。

1 双层规划模型框架

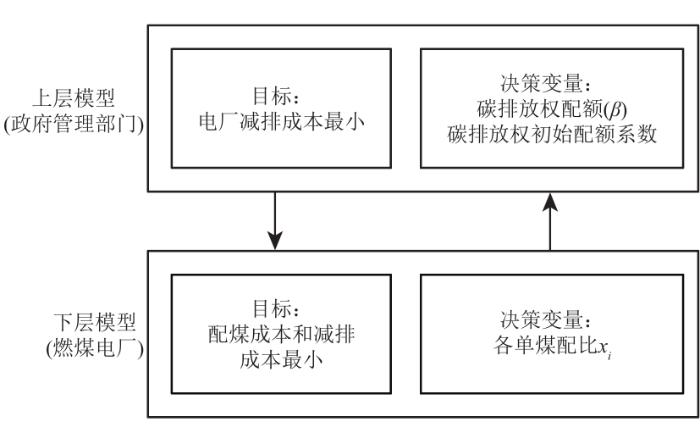
在制定配煤掺烧计划的过程中，政府管理部门和电厂燃料部门都要参与决策。而政府管理部门具有更高的优先权，希望在一定碳排放总量的前提下使当前电厂减排成本最小，这会影响当前电厂的配煤生产计划和碳减排决策。电厂根据政府管理部门的决策来制定当前的煤炭掺烧发电计划，希望使其成本最小。然而，电厂也会反过来影响政府管理部门，使政府管理部门重新考虑最初的决策，并对其制定的计划进行调整。这种政府部门与发电企业的决策交互会不断更迭，直到找到双方满意的解决方案，这被表述为双层规划模型^[13-14]，其结构如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 双层规划模型结构图

Fig. 1 Structure diagram of bi-level programming model

政府管理部门根据生产计划为电厂分配碳排放配额，为控制碳排放量，政府管理部门必须确保分配量达到减排目标，进而达到减排成本最小的目的。而电厂生产排放必须更加环保才能争取到更多的碳排放配额，更多的碳排放配额意味着电厂将有更高的产量和更好的经济效益。所以，在当前配额分配机制下，电厂追求更高的排放绩效，以达到清洁环保型电厂。对环保性而言，煤的含碳量越高，不能燃烧的杂质含量越低，挥发分就越少，排放的污染物气体越少。因此，优质煤成为达到环保要求的首选煤种，但煤的成本也会增加，这就导致如果电厂只依赖于优质煤种，排放性能会有所提高，但导致净收益下降，而选择多煤种掺烧的方式是解决这一困境的有效手段。

2 模型的建立

2.1 上层规划模型

政府管理部门的目标是在确保碳排放分配量达到减排目标不超过碳排放配额总量的前提下，实现电厂减排成本最低。因此，政府管理部门面临的优化问题是如何合理分配碳排放权初始配额，使得电厂减排成本达到最小。因此，上层模型构建需基于碳排放配额总量前提下的电厂减排成本最小化函数。

目标函数

m i n S = Z - k δ^{2} n^{2}

(1)

式中： $S$ 为电厂减排成本； $Z$ 为碳减排固定投入金额； $k$ 为可变减排成本系数； $δ$ 为单位发电量对应的最优碳排放配额； $n$ 为电厂单位时间内的发电量。

约束条件

0 < δ < m a x δ

(2)

式(2)表示政府管理部门分配的碳排放权初始配额不得超过区域内电厂最大单位碳排放强度。

2.2 下层规划模型

如何合理地在碳减排决策的约束下使得电厂综合成本最小化，是电厂部门追求的目标。因此，在满足配煤质量指标的前提下，考虑混煤的发热量、排放特性、煤质特性等因素，以配煤成本和碳排放成本最低为目标来构建下层规划模型。

2.2.1 下层规划目标函数

m i n J = \sum_{i = 1}^{q} P_{i} \times x_{i} + c_{c} (δ^{*} n - δ n)

(3)

式中： $J$ 为配煤成本和碳排放成本之和，若碳排放成本>0，表示碳排放配额不足，需在市场买入。若碳排放成本<0，表示碳排放配额有剩余，可从中获利； $P_{i}$ 为单煤的价格； $x_{i}$ 为单煤的掺配比例； $c_{c}$ 为碳交易配额价格； $δ^{*}$ 为电厂单位电量的碳排放强度。

2.2.2 下层规划约束条件

本文从锅炉燃烧、安全、污染物排放及锅炉设计指标建立混煤煤质约束条件。若混煤煤质波动大，将引起运行参数调整难度增加，给机组安全运行带来隐患^[15]，会严重影响锅炉稳定性，甚至会导致严重事故。为确保锅炉的长期安全稳定运行，必须考虑燃料特性。发热量指标对煤粉稳定燃烧有着很大影响，灰分关系着混煤的结渣特性，硫分的含量关系着混煤污染物排放中产生的SO₂，因此，可通过约束混煤煤质特性和调整实际工况来达到锅炉对燃烧、安全及污染物排放指标的要求。

约束条件如式(4)—(9)所示。其中，式(4)—(8)以锅炉的燃烧特性、排放特性、混煤煤质参数作为约束条件，式(9)为单煤比例约束。

发热量：

Q_{m i n} \leq f_{Q} (Q_{i}, x_{i}) \leq Q_{m a x}

(4)

挥发分：

V_{m i n} \leq f_{V} (V_{i}, x_{i}) \leq V_{m a x}

(5)

灰分：

A_{m i n} \leq f_{A} (A_{i}, x_{i}) \leq A_{m a x}

(6)

水分：

M_{m i n} \leq f_{M} (M_{i}, x_{i}) \leq M_{m a x}

(7)

硫分：

S_{m i n} \leq f_{S} (S_{i}, x_{i}) \leq S_{m a x}

(8)

单煤比例之和：

\sum_{i = 1}^{q} x_{i} = 1

，且

x_{i} \geq 0

(9)

式中： $Q_{m i n}$ , $V_{m i n}$ , $A_{m i n}$ , $M_{m i n}$ , $S_{m i n}$ 分别为发热量、挥发分、灰分、水分、硫分的最小值； $Q_{m a x}$ , $V_{m a x}$ , $A_{m a x}$ , $M_{m a x}$ , $S_{m a x}$ 分别为发热量、挥发分、灰分、水分、硫分的最大值。

2.3 双层规划模型

通过式(1)—(9)制定全局优化模型，该模型的优化过程可以概述为：根据历史数据和自身需求目标，政府管理部门决定初始碳排放分配方案。将分配方案下发电厂后，电厂制定配煤计划，将锅炉的燃烧特性、排放特性、混煤煤质要求作为限制条件。当所有参与者都试图根据自身目标制定计划时，就会出现冲突。然而，每一方的决定都会影响双方的决策。电厂的配煤计划提交到政府管理部门后，政府管理部门再根据电厂的排放绩效对其碳排放分配方案进行调整改进。电厂再次根据新的配额重新考虑之前的配煤计划，并向管理部门提交改进的配煤计划。重复这个过程，直到所有利益相关者达成共识后，就形成了均衡的解决方案。

本文建立针对碳减排配煤优化问题的双层规划模型：

\{\begin{array}{l} m i n S = Z - k δ^{2} n^{2} \\ m i n J = \sum_{i = 1}^{q} P_{i} x_{i} + c_{c} (δ^{*} n - δ n) \\ s . t . 0 < δ < m a x δ \\ Q_{m i n} \leq f_{Q} (Q_{i}, x_{i}) \leq Q_{m a x} \\ V_{m i n} \leq f_{V} (V_{i}, x_{i}) \leq V_{m a x} \\ A_{m i n} \leq f_{A} (A_{i}, x_{i}) \leq A_{m a x} \\ M_{m i n} \leq f_{M} (M_{i}, x_{i}) \leq M_{m a x} \\ S_{m i n} \leq f_{S} (S_{i}, x_{i}) \leq S_{m a x} \\ \sum_{i = 1}^{q} x_{i} = 1 \end{array}

(10)

建立上述双层规划模型目的是确定电厂配煤掺烧工作的最优配煤比、减少配煤成本和减排成本。为了增强该模型在类似情况下的适用性，提出以下建议：

1）在该双层规划模型中，减排系数k是由政府部门控制的参数。采用调整控制参数的方法，可以使管理部门决策更加灵活，可确定令人满意的决策方案。

2）可通过更改、增加目标函数，使该模型适用范围更广泛。例如，当政府管理部门注重从碳排放配额分配中获得税收和财政收入时，可增加目标函数，使政府部门财政收入最大化。

3）可通过更改、增加或删除一些约束条件使其更有针对性。例如，对于对煤炭质量要求(即污染物特性、燃烧特性等)较严格的电厂，可添加特定约束条件，使该模型与实际情况相匹配。

3 求解算法

针对上述双层规划模型的目标函数和各种约束条件，在使用标准粒子群优化(particle swarm optimization，PSO)算法进行优化求解时，在寻优过程中极易陷入局部最优解的问题，因此，本文将混沌思想引入粒子群算法中对该规划模型进行寻优。

3.1 混沌粒子群算法优化

粒子群算法是用于解决全局优化问题的模拟鸟群捕食行为的一种群智能进化算法^[16]。粒子群算法简单，易于求解优化问题，然而优化性能很大程度上由其参数所决定，容易出现陷入局部最优解、进化速度较慢等现象。因此，引入基于logistic方程的混沌粒子群优化方法，来解决陷入局部最优的问题。通过混沌扰动避免出现局部最优，并采用自适应惯性权重来加快收敛速度，混沌粒子群的随机性和遍历性克服了传统粒子群算法的不足，可对规划模型进行优化求解。在混沌局部搜索过程中，使用了以下logistic有限差分方程：

w_{j + 1} = μ w_{j} (1 - w_{j})

(11)

式中： $μ$ 为控制参数，通常将 $μ$ 设为4； $w_{j}$ 表示第j个混沌变量，其输出[0, 1]范围内的随机变量，遍历区间[0, 1]的每个不重复的数。

3.2 混沌粒子群算法求解

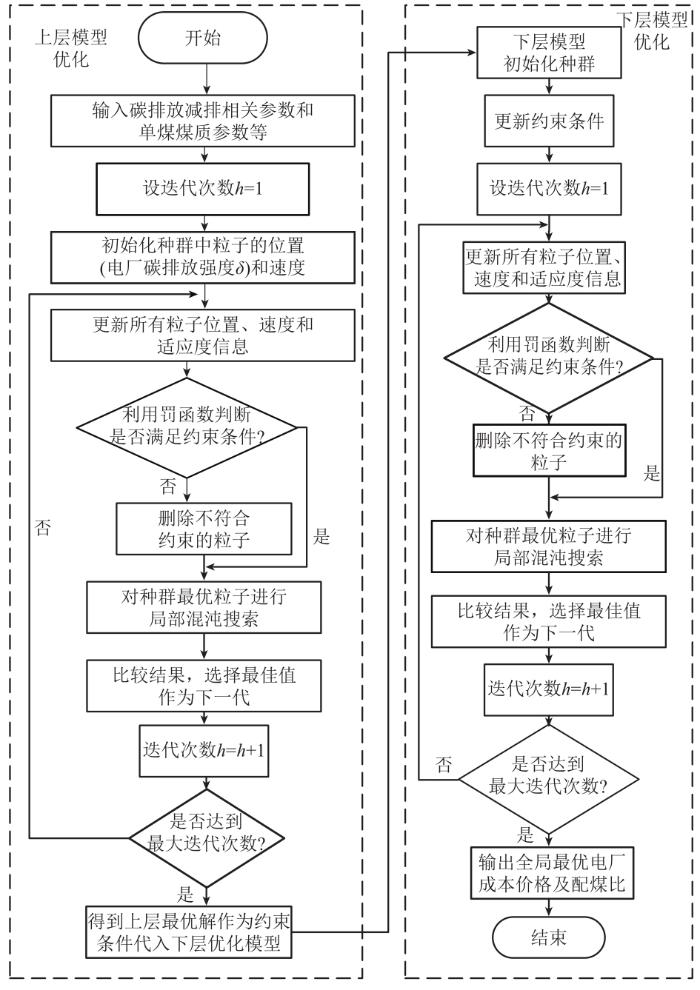
通过两阶CPSO算法之间的协同迭代，实现同步优化双层规划的上下层。将上层的解代入下层模型，通过下层的目标函数和约束条件，在一定范围内求得一个最优解。将结果反馈给上层，上层在下层优化的基础上，根据目标函数和约束条件求得整体最优解。两层之间相互迭代，求得全局近似最优解。混沌粒子群算法求解双层规划模型的流程图如图2所示，基本步骤如下。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 CPSO求解双层规划模型流程图

Fig. 2 Flow chart of CPSO solving bi-level programming model

Step1：初始化CPSO算法中的参数，设置学习因子C₁、C₂，粒子数、迭代次数、混沌步数等参数，随机产生上层模型约束条件的初始解，随机初始化粒子的位置 $p_{i}$ 和速度 $v_{i}$ ， $i \in [1, N]$ ，N为粒子的个数。

Step2： $x_{B e s t}$ 是第 $i$ 个粒子的当前位置， $z_{B e s t}$ 为初始种群粒子的最佳位置。

Step3：对种群中的所有粒子，执行如下操作。

① 更新粒子位置和速度，通过罚函数对约束条件进行限制。

② 将上层模型的解粒子 $i$ 的位置 $p_{i}$ (即碳排放强度)代入下层模型，采用CPSO算法求解下层模型的最优解 $y_{i}$ 。

③ 将 $(p_{i}, y_{i})$ 代入上层规划的目标函数，计算出函数值，即粒子 $i$ 的适应度 $F (p_{i}, y_{i})$ 。

④ 如果更新后的适应度比 $x_{B e s t}$ 的适应度高，则用 $p_{i}$ 代替 $x_{B e s t}$ ，对应的 $x_{B e s t}$ 的下层模型最优解 $y_{i}$ 替代 $y x_{B e s t}$ 。

⑤ 如果更新后的适应度比 $z_{B e s t}$ 的适应度高，则用 $p_{i}$ 代替 $z_{B e s t}$ ，对应的 $z_{B e s t}$ 的下层模型最优解 $y_{i}$ 替代 $y z_{B e s t}$ 。

Step4：对种群的最优粒子进行局部混沌搜索。

Step5：更新下一代粒子的个体极值和种群极值。

Step6：若此时函数已收敛并达到最优解，跳转到Step8，否则转Step7。

Step7：更新 $z_{B e s t}$ ，采用CPSO算法求初下层模型的最优解 $y z_{B e s t}$ ，并转Step3。

Step8：输出双层规划模型的最优解 $z_{B e s t}$ 和 $y z_{B e s t}$ ，求出上下层规划的目标函数最优解。

4 实例分析

4.1 算例介绍

基于上述所建立的模型和算法，选用某电厂常用的10种单煤煤种^[17-18]进行掺烧优化研究，各单煤煤质参数如表1所示，锅炉设计煤种参数如表2所示。

表1 单煤数据库

Tab. 1 Single coal database

编号	M_ar/%	A_ar/%	V_ar/%	S_ar/%	Q/(MJ⋅kg^-1)	P/(元/t)
M1	1.14	30.58	11.05	0.4	20.69	638.29
M2	2.09	36.28	7.61	0.72	18.38	487.47
M3	1.82	33.24	22.83	3.66	16.78	405.54
M4	2.39	29.52	6.25	0.42	21.04	494.00
M5	0.76	24.71	12.72	0.35	23.09	624.00
M6	0.51	32.27	14.96	2.99	20.28	515.14
M7	1.72	38.88	7.83	0.57	18.50	506.00
M8	0.94	28.98	12.23	1.24	21.29	734.08
M9	2.07	47.23	9.98	1.14	15.16	409.86
M10	3.23	33.49	9.04	1.91	18.45	519.53

注：M_ar为收到基水分；A_ar为收到基灰分；V_ar为收到基挥发分；S_ar为收到基硫分；Q为热值；P为价格。

新窗口打开| 下载CSV

表2 锅炉设计煤种参数值

Tab. 2 Boiler design coal parameter value

煤质特性	M_ar/%	A_ar/%	V_ar/%	S_ar/%	Q/(MJ⋅kg^-1)
设计值	1.42	26.4	17.1	0.8	21.35

新窗口打开| 下载CSV

上海某电厂单位时间内平均发电量 $n$ 为510 MW⋅h，在不失一般性的前提下，假设电厂投入的碳减排固定资本投入 $Z$ 为12 000元，选取可变碳减排成本系数 $k$ 为0.025，单位碳排放强度 $δ^{*}$ 参考文献[19]，选取0.82 t/(MW⋅h)，参考上海火电上网电价碳配额价格， $c_{c}$ 选取40元/t。

4.2 计算结果与分析

将4.1节的参数代入本文所构建的双层规划模型中，利用CPSO算法进行求解，算法参数设置如下：C₁=C₂=2，粒子数为200，h=200，混沌搜索最大步数为50，仿真用MatlabR2017b实现。

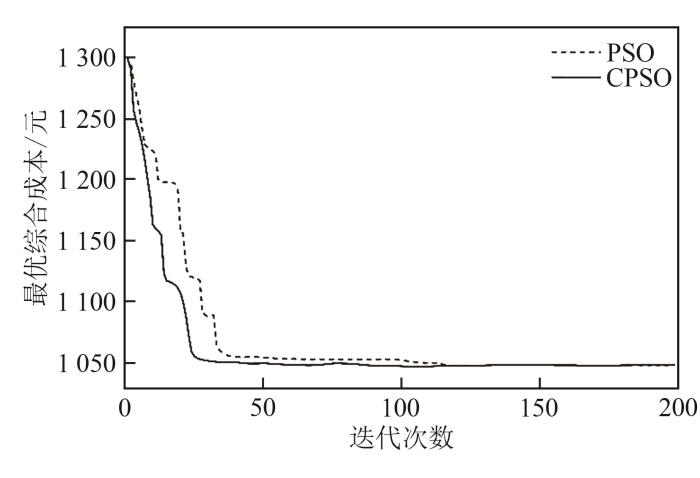
为验证CPSO算法的优越性，本文将其和PSO算法进行寻优求解对比，2种算法的迭代过程如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 2种算法迭代过程对比图

Fig. 3 Comparison diagram of iterative process of two algorithms

通过图3结果可以看出，在2种算法寻优结果相同的前提下，CPSO算法收敛速度较快、波动较小，收敛寻优效果更好，由此可以得出CPSO算法相较于普通PSO算法在解决该问题上具有一定的优越性。故根据CPSO算法求解该模型，运用MATLAB求解得到最优配煤比例为17%M7、12%M4、71%M9，将3种煤种进行掺配，可得到最优配煤成本为436.3元/t，比大部分单煤单价要低。

同时，计算得到与最优配煤比对应的最优碳排放配额δ，最优碳排放配额下的最小减排成本、碳排放成本和综合成本，结果如表3所示。

表3 最优配煤比下发电机组相关结果

Tab.3 Related results of generator set under optimal coal blending ratio

参数	碳排放配额/[t/(MW⋅h)]	减排成本/元	碳排放成本/元	综合成本/元
数值	0.79	7 941.79	612	1 048.3

新窗口打开| 下载CSV

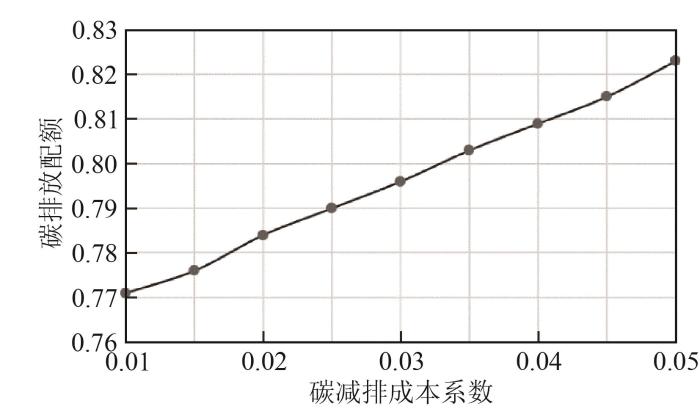
进一步分析，由于碳减排系数是可变的，故由碳减排函数与碳排放配额的关系(图4)可以看出，在其他参数不变的情况下，碳排放配额随着碳减排系数增加而增加，两者呈正相关关系。而碳减排系数的增加意味着有更低的碳减排和碳排放成本，这需要电厂有相对更好的排放表现来争取到更多的配额。尽管这种行为会导致单位生产成本的增加，但对电厂而言，恰恰可以通过合理调整配煤比例来改善排放性能，控制生产成本，使得总排放量减小。对政府管理部门而言，碳排放配额设置越宽松，减排成本越高，故政府管理部门应同步缩紧碳排放配额管控力度。但为了鼓励经济发展，政府管理部门可以在开始设定相对宽松的减排目标，一段时间后，可通过收紧碳减排系数来达到严格的环保要求。这一结果对今后政府管理部门合理调整碳排放配额和电厂制定配煤计划具有现实指导意义。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 碳减排系数与碳排放配额的关系

Fig. 4 Relationship between carbon emission reduction coefficient and carbon emission quota

5 结论

提出了一种基于双层规划的碳减排配煤优化方法，以实现燃煤电厂的碳排放控制和配煤优化，所得结论如下：

1）通过双层规划模型的方式既考虑到政府管理部门的碳减排目标，又考虑到燃煤电厂的配煤和碳排放成本，两者可以互相协调，并实现电厂配煤优化和掺烧方案的选择。

2）利用混沌粒子群算法求解双层规划模型，与普通粒子群算法相比具有更好的收敛效果，在求解该问题上具有一定的优越性。

3）当面临碳排放配额限制时，配煤掺烧的方法可以帮助电厂优化其发电计划，进而优化碳排放配额的分配机制，为实现“碳中和、碳达峰”目标提供一种思路。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

刘志强，潘荔，赵毅，等．

“十四五”时期我国火电行业节能潜力分析与建议

[J]．中国能源，2021，43(4)：12-18．