0 引言
随着“2030年碳达峰、2060年碳中和”能源发展目标的提出,能源转型加速推进,综合能源系统因其在促进清洁能源消纳、提升能源利用率和降低用能成本方面的显著作用,已成为满足多能供需的新的能源利用实现方式。从地理范围上讲,综合能源系统可以划分为局域级[1 -4 ] (如楼宇、社区、工厂等)、区域级[5 -8 ] (如城区)和广域级[9 -10 ] (如城市、跨区域、跨国等)。园区综合能源系统(community integrated energy system,CIES)[11 -13 ] 作为典型的局域级综合能源系统,通过建立电力、天然气、可再生能源等多种能源之间的耦合利用关系,可以显著提高能源综合利用效率、降低用能成本和减少碳排放量,为实现低碳园区建设提供了一种有效途径。因此,开展CIES规划研究具有重要意义。
现有CIES规划的研究主要集中于能源站内设备选型和定容,大致可以划分为2个阶段。第一个阶段为单纯的规划模型优化研究阶段,如:文献[14 ]中以电-气综合能源系统作为研究对象,通过建立电气耦合模型优化得到能源站容量配置;文献[15 ]中同时对多个能源站进行规划,充分考虑能源站内不同形式能源耦合和不同能源站间的互联关系,优化得到各能源站的容量配置;文献[16 ]中建立了综合能源系统主要设备的能量流模型,并在此基础上利用改进Kriging模型对系统进行规划优化,计算得到系统最佳规划方案等。以上文献虽对综合能源系统进行规划,但都是只考虑系统的规划优化,未涉及系统运行优化。
第二个阶段为协同规划优化研究阶段,在进行规划的同时考虑系统运行经济性、环保性等,使得规划的结果更具实用性,如:文献[17 ]考虑站-网协同,构建了CIES双层规划优化模型,上层规划求解能源站数量、位置和容量,下层通过建立多能源站规划运行联合优化模型对系统运行进行优化,优化结果返回上层进行更新;文献[18 ]考虑源-荷互动,建立了CIES站-网协同双层规划优化模型,规划结果相较于文献[16 ]更加经济合理;文献[19 ]对多区域综合能源系统规划进行研究,提出了一种两阶段优化方法,通过优化系统的经济和环境成本求解各区域能源容量配置。上述文献在进行系统规划的同时考虑了系统运行优化,但也存在一定的局限性,如规划模型建模普遍简单,为单目标优化问题;系统供能结构单一,候选设备类型较少;普遍只考虑了系统运行时的经济性和环保性,而对于系统运行时的其他重要因素(如负荷供给可靠性)考虑较少等。
针对现有CIES规划研究存在的不足,本文充分考虑系统运行时多项因素(经济性、环保性、负荷供给的可靠性),建立了CIES两阶段优化模型。第一阶段研究了能源站设备类型及定容问题,第二阶段研究了系统运行优化问题。第一阶段利用带精英保留策略的二代非支配排序遗传算法(non-dominated sorting genetic algorithm II,NSGA-II),分别以系统规划年经济成本和年环境成本最小为优化目标,规划求解系统设备类型及容量;第二阶段主要针对第一阶段得到的多组帕累托前沿解,以系统运行经济和环境总成本最低为优化目标,利用混合整数线性规划(mixed integer linear programming,MILP)优化求解各规划方案对应系统运行时设备出力及运行成本;在此基础上,针对不同规划方案计算其负荷供给可靠性指标,最终实现计及负荷供给可靠性的系统协同规划优化。
1 CIES两阶段协同规划优化模型
1.1 模型结构
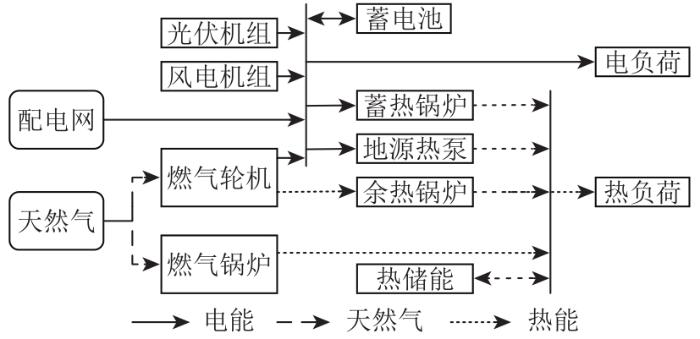
本文以河北雄安新区某园区冬季供暖期为例,进行CIES协同规划优化研究。园区所在位置附近建有1座220 kV变电站可为其供电,霸保管线是目前新区的主要天然气管线设施,可为园区供气,同时雄安地区具有较好的中深层地热资源,可用于园区供热系统,太阳能和风能资源条件中等,可与园区其他能源耦合互补。园区供暖期系统供能结构如图1 所示。在供电系统中,除直接从外部购电外,园区可以利用热电联产装置(combined heat and power,CHP)、光伏(photovoltaic,PV)、风机(wind turbin,WT)联合互补运行供电,保障供电稳定性;在供热系统中,电力可用于蓄热电锅炉(electric boiler,EB)和地源热泵(ground source hear pump,GSHP)实现电、地热供热,天然气可用于CHP和燃气锅炉(gas boiler,GB),实现燃气供热,通过电、气联供供热保障园区供热的可靠性;同时,通过安装电储(electric storage,ES)和热储(heat storage,HS)实现用能低谷时存储、用能高峰时释放的功能,提高系统的经济性和灵活性。
图1
图1
园区供暖期系统供能结构图
Fig. 1
Structure diagram of community energy supply in the heating period
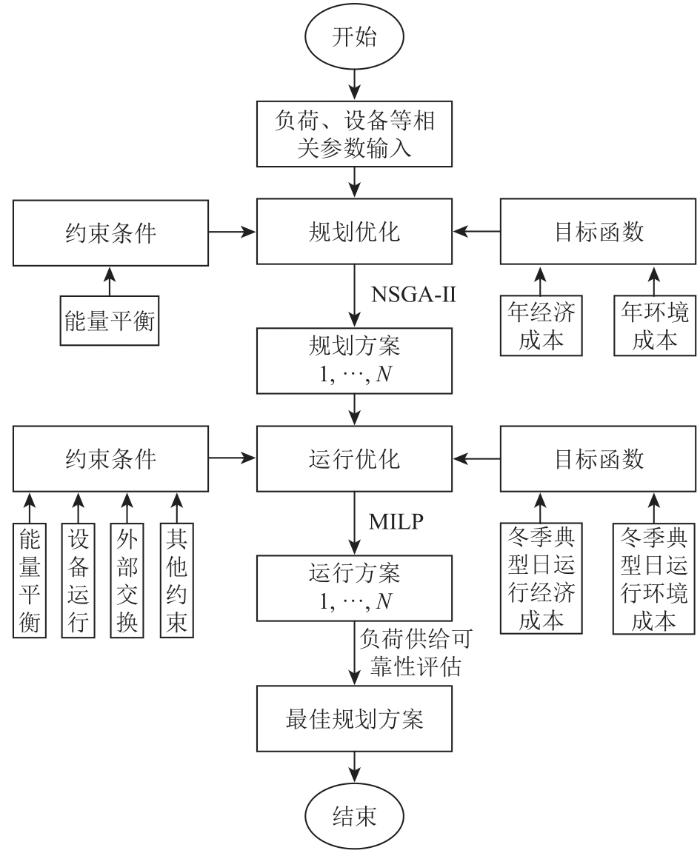
针对上述园区供暖期供能结构,本文采用两阶段优化方法进行规划优化,同时考虑系统运行的经济性、环保性和负荷供给的可靠性,以使得规划结果更加符合实际情况。系统优化流程如图2 所示:第一阶段为系统规划优化阶段,决策变量为园区综合能源站设备类型及容量,以能量平衡为约束条件,目标是使能源站的投资维护成本和环境成本最小;第二阶段为系统运行优化阶段,决策变量为能源站各设备出力及与外部电网交互功率,以能量平衡、设备运行、外部交换功率等为约束条件,目标是使系统运行的经济性和环保性最优,同时以系统运行时负荷供给的可靠性作为重要指标,并将计算结果反馈至第一阶段,作为确定系统最佳规划方案的重要参考。
图2
图2
园区供暖期系统优化流程图
Fig. 2
System optimization flow chart in the community heating period
1.2 第一阶段规划优化模型
1.2.1 目标函数
第一阶段规划优化模型为多目标函数优化模型,目标函数包括年经济成本和年环境成本。年经济成本主要由能源站年投资成本和年能源消费成本组成,即
m i n f 1 = m i n ( C i n v + C e n e ) (1)
C i n v = ∑ i C i n v , i C R F n , i (2)
C R F n = r ( 1 + r ) n ( 1 + r ) n - 1 (3)
C e n e = ∑ d ∑ t τ d [ π e l e , t P g r i d , t + π g a s , t ( P c h p , t + P g b , t ) ] (4)
式中:f 1 表示能源站年经济成本;C inv 表示能源站年投资成本;C ene 表示年能源消费成本;C i n v , i i 的年投资成本;C R F n r 表示资本年利率;τ d d 的数量;π e l e , t π g a s , t t 时刻的电价和气价;P g r i d , t P c h p , t P g b , t t 时刻消耗的电、热和天然气功率。
m i n f 2 = m i n C e n v (5)
C e n v = ∑ j ∑ d ∑ t τ d θ j [ P g r i d , t w g r i d , j + w g a s , j ( P c h p , t + P g b , t ) ] (6)
式中:f 2 为系统年环境成本;C e n v θ j j 类污染物排放成本;w g r i d , j w g a s , j j 类污染物单位排放系数。
1.2.2 约束条件
针对图1 中供能结构,第一阶段规划优化模型中的约束条件主要为系统能量平衡。园区供暖季典型日电、热能量平衡约束为:
P p v , t + P w t , t + P g r i d , t + P c h p , t η c h p , e + P e s d , t = P e l e , t + P e s c , t + P e b , t + P h b , t (7)
P c h p , t η c h p , h + P g b , t η g b , h + P e b , t η e b , h + P h b , t η c o p , h + P h s d , t = P h , t + P h s c , t (8)
式中:P p v , t P w t , t P e s d , t t 时刻光伏、风机发电功率和蓄电池放电功率;η c h p , e P e l e , t t 时刻电负荷;P e s c , t P e b , t P h b , t t 时刻蓄电池充电、蓄热电锅炉和地源热泵的耗电功率;η c h p , h η g b , h η e b , h η c o p , h P h s d , t t 时刻热储能放热功率;P h , t t 时刻热负荷;P h s c , t t 时刻热储能储热功率。
1.3 第二阶段运行优化模型
1.3.1 目标函数
第二阶段运行优化模型从系统运行层面出发,以电交易、系统运维和污染物排放最少为优化目标建立函数优化模型,即
m i n f 3 = m i n ( C e n + C o p + C e v ) (9)
C e n = ∑ t π e l e , t P g r i d , t + π g a s , t ( P c h p , t + P g b , t ) (10)
C o p = ∑ i ∑ t π i P i , t (11)
C e v = ∑ j ∑ t θ j [ P g r i d , t w g r i d , j + w g a s , j ( P c h p , t + P g b , t ) ] (12)
式中:f 3 为系统总运行成本;C e n C o p C e v π i i 单位运行成本;P i , t t 时刻设备i 的出力。
1.3.2 约束条件
能量平衡约束指系统运行时供、需能量平衡,具体约束条件与1.2.2节相同。
设备运行约束指设备运行过程中的一些约束条件,如设备最大出力约束、设备最多启停次数等。基于图1 中供暖期系统供能结构图,设备运行约束条件如下:
P p v , t = I s , t S p v N p v η p v (13)
式中:P p v , t t 时刻功率;I s , t t 时刻光照强度;S p v N p v η p v
0 ≤ S p v N p v ≤ S p v , m a x (14)
0 ≤ P w t , t ≤ P w t , m a x N w t (15)
式中:P w t , m a x N w t
蓄电池采用通用储能模型,约束条件主要包括能量平衡约束、存储能量上下限约束以及充放功率约束,具体如下:
P e s , t + 1 = P e s , t + ( P e s c , t η e s c - P e s d , t η e s d ) Δ t (16)
P e s , m i n N e s ≤ P e s , t ≤ P e s , m a x N e s (17)
0 ≤ P e s c , t ≤ P e s c , m a x N e s (18)
0 ≤ P e s d , t ≤ P e s d , m a x N e s (19)
式中:P e s , t t 时刻蓄电池储电量;η e s c η e s d N e s P e s , m i n P e s , m a x P e s c , m a x P e s d , m a x
0 ≤ P c h p , t η c h p , e ≤ P c h p , m a x N c h p (20)
0 ≤ P c h p , t η c h p , h ≤ H c h p , m a x N c h p (21)
式中:P c h p , m a x H c h p , m a x N c h p
0 ≤ P g b , t η g b , h ≤ H g b , m a x N g b (22)
式中:H g b , m a x N g b
0 ≤ P e b , t η e b , h ≤ H e b , m a x N e b (23)
式中:H e b , m a x N e b
0 ≤ P h b , t η c o p , h ≤ H h b , m a x N h b (24)
式中:H h b , m a x N h b
热储能同样采用通用储能模型,约束条件主要包括能量平衡约束、存储能量上下限约束以及充放功率约束,具体如下:
P h s , t + 1 = P h s , t + ( P h s c , t η h s c - P h s d , t η h s d ) Δ t (25)
P h s , m i n N h s ≤ P h s , t ≤ P h s , m a x N h s (26)
0 ≤ P h s c , t ≤ P h s c , m a x N h s (27)
0 ≤ P h s d , t ≤ P h s d , m a x N h s (28)
式中:P h s , t t 时刻热储能装置储热量;η h s c η h s d N h s P h s , m i n P h s , m a x P h s c , m a x P h s d , m a x
P g r i d , t ≤ P g r i d , m a x (29)
式中P g r i d , m a x
1.3.3 考虑设备变工况特性
考虑到系统设备实际运行时受环境等多种因素影响,上述优化模型在构建时对系统关键设备的变工况特性进行充分考虑。其中,CHP机组和燃气锅炉受环境温度影响较小,其运行工况主要受负载率影响,设备实际运行效率与负载率的关系可以表示为
η x = η x r a t e d ∑ k = 0 n a x , k N x k (30)
式中:η x η x r a t e d a x , k N x
地源热泵温变特性明显,其运行受负载率影响较小,实际运行效率与温度的关系为
η c o p = η c o p r a t e d ∑ k = 0 n b h b , k τ k (31)
式中:η c o p r a t e d b h b , k τ
1.4 供能可靠性评估指标
除了经济性和环保性,进行容量优化配置时还应考虑系统的供能能力,即负荷供给可靠性。本文通过评估能源供应和负荷需求的匹配程度来度量系统的负荷供给可靠性,设计了平均负荷偏差率作为评估指标,具体如下:
L e l e , t = P e l e , t - P w t , t - P p v , t - P c h p , t η c h p , e (32)
L h , t = P h , t - P e b , t η e b , h - P h b , t η c o p , h - P g b , t η g b , h - P c h p , t η c h p , h (33)
L R e l e = 1 T ∑ t = 1 T L e l e , t P e l e , t × 100 % (34)
L R h = 1 T ∑ t = 1 T L h , t P h , t × 100 % (35)
L R = 1 2 ( L R e l e + L R h ) (36)
式中:L e l e , t L h , t t 时刻系统电、热负荷供给偏差量;L R e l e L R h T 时间段内系统电、热负荷供给平均偏差率;L R
2 模型求解算法
第一阶段规划优化模型是多目标优化问题,目标函数分别为最小化年经济成本f 1 和最小化年环境成本f 2 ,可以直接通过Pareto最优解进行求解,而无需转化为单目标优化问题,避免了因目标函数合并不合理(如权重设置不合理等)而引起的计算误差。NSGA-II是一种基于Pareto最优解的多目标优化算法,对于难以求解的优化问题,通常仍能找到较优解且算法具有较好的收敛性[20 ] ,这里考虑带有精英保留策略的NSGA-II算法进行模型求解。
第一阶段规划模型求解的目的是确定能源站中各设备的配置容量P=Px, max Nx ,x 表示设备,根据图1 中的候选能源设备种类,该解可表示为长度为9的向量 x x 1 , x 2 ,…, x 9 )。设种群为R ,种群大小为K ,种群进化代数为g ,目标函数为fm (m =1,2),个体拥挤度为nr (r =1,…,K ),其计算公式为
n r = n r + [ f m ( i + 1 ) - f m ( i - 1 ) ] / ( f m m a x - f m m i n ) (37)
式中:fm (i +1)是排序后该个体后一位目标函数值;f m m a x f m m i n fm 的最大值和最小值。具体算法流程如下:
1)系统参数初始化,输入电热负荷、设备参数、光照强度、风速等系统参数。
3)对种群Rg 快速非支配排序,划分为不同Pareto等级。
4)计算年经济成本f 1 (g )、年环境成本f 2 (g ),并按照式(37)计算Rg 中各个体拥挤度n r ( g )
5)对种群Rg 进行遗传操作,选择、交叉、变异,产生一代子群Qg 。
6)将Rg 与Qg 合成种群Wg ,对Wg 进行快速非支配排序,划分为不同Pareto等级,并计算Wg 中各个体拥挤度n w ( g )
7)按以下规则从种群Wg 生成新一代种群Rg +1 :①根据Pareto等级将整层Wg 放入Rg +1 ,直到某一层个体不能全部放入Rg +1 ;②将该层个体根据拥挤度从大到小排序,依次放入Rg +1 中,直到填满为止。
8)g =g +1,判断是否满足迭代终止条件:如不满足,则返回步骤3);如满足,则输出规划结果 x f 1 、环境成本f 2 。
第一阶段规划模型求解通常会得到多组Pareto最优解,即多个规划方案,为确定最佳规划方案,第二阶段针对各组解(规划方案)开展系统运行优化分析,目标函数为最小化系统典型日运行、维护和污染物排放成本f 3 ,为单目标优化问题。考虑到约束条件中Nx 须为整数,因此第二阶段运行优化问题为典型的混合整数线性规划问题[21 ] ,决策变量为典型日各设备实时运行出力Px , t x 为该规划方案下系统运行设备,设其类别数为c ,t 表示01:00—24:00运行整点时刻,则该解可以表示为c ×24的矩阵 X f 3 。
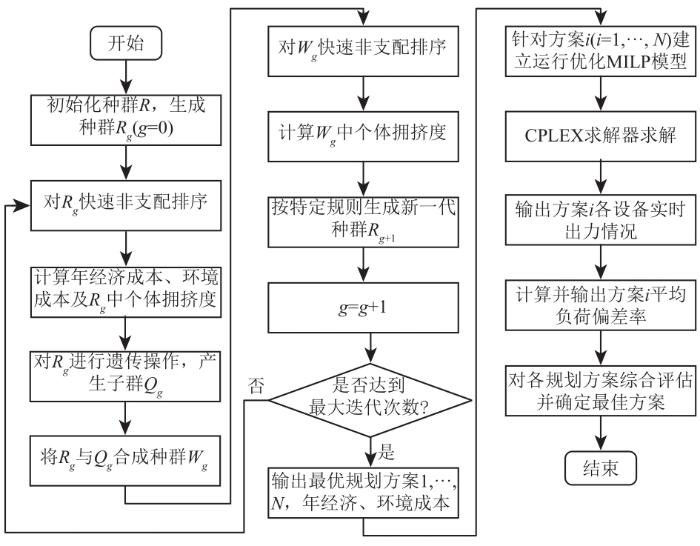
在第二阶段模型优化求解的基础上,针对各规划方案计算其平均负荷偏差率L R ,以评估方案供能的可靠性。在上述基础上,通过对各规划方案进行综合量化评估以确定最佳方案。模型求解算法流程如图3 所示。
图3
图3
模型求解算法流程图
Fig. 3
Flow chart of model solving algorithm
3 算例分析
3.1 算例说明
本文以河北雄安新区某园区综合能源系统为研究对象,该园区主要包括会议中心、行政办公、生活服务中心、专家公寓和商务酒店共5种不同业态。考虑到该园区可利用资源形式,其冬季供暖期供能结构如图1 所示。
为了验证规划结果的合理性,增加了以气为主供能和传统以电为主供能2种场景作为对比。以气为主的多能耦合供能方案,主要通过燃气三联供机组进行用户负荷的供应,由外网购电辅助补充供能;传统以电为主供能方案,主要通过外网购电和以电制热满足用户负荷需求,由光伏以及储能装置配合出力。各场景具体配置如表1 所示:场景1为结合雄安新区可利用资源形式设计的园区候选设备种类;场景2和场景3分别为以气为主和以电为主的候选设备种类,主要用作对比。
3.2 规划及运行优化结果分析
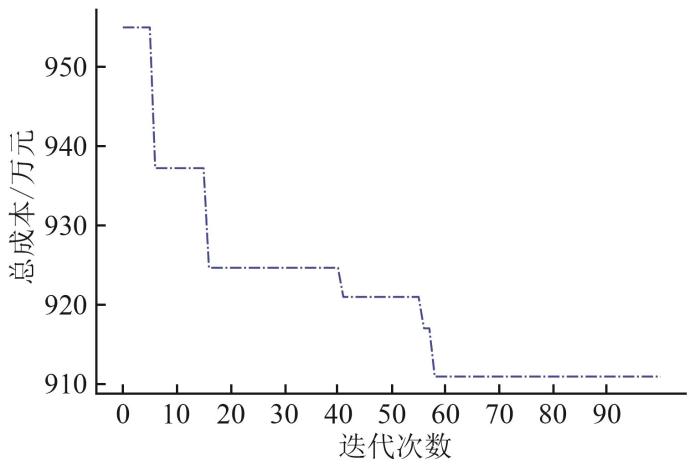
针对场景1进行规划,利用带精英保留策略的NSGA-II算法对第一阶段规划模型求解,实现年经济成本f 1 和年环境成本f 2 的协同优化,算法参数设置如下:种群数量为100,迭代最大次数为100,交叉概率为0.85,变异概率为0.5。算法迭代收敛过程如图4 所示,得到的Pareto最优解集(前沿解)如图5 所示。
图4
图4
NSGA-II算法迭代收敛过程
Fig. 4
Iterative convergence process of NSGA-II algorithm
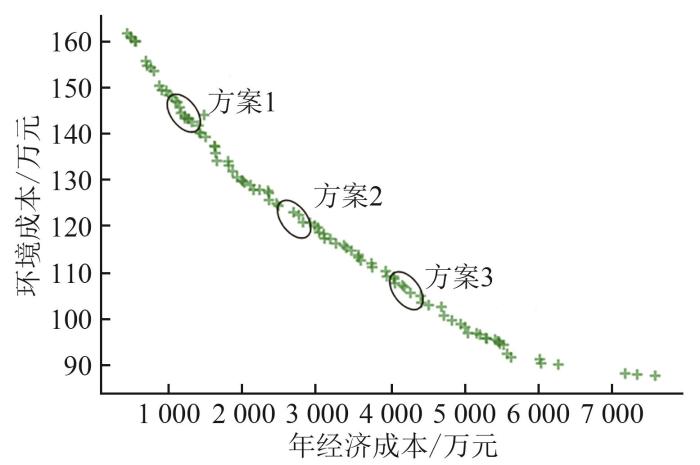
图5
图5
第一阶段规划模型Pareto前沿解
Fig. 5
Pareto frontier solution of the first-stage planning model
从图4 可以看出,当迭代次数达到第58次时算法趋向于收敛,具有较快的收敛速度。从图5 可以看出,环境成本随着经济成本的增加逐渐降低,二者之间呈反比关系。从Pareto最优解集中选取3组代表性最优解(即低经济成本、高环境成本,中经济成本、中环境成本以及高经济成本、低环境成本),如图5 所示,对应形成的3种规划方案容量配置情况如表2 所示。
雄安的光能和风能的评级为中等,由于PV的安装成本较低,故3个方案均配置了PV,且园区安装面积有限,PV的安装容量均达到上限值1 MW;由于候选设备中同时存在EB以及GSHP,且EB的能量转换效率远不如GSHP,故3个方案都选择以GSHP供热为主。对比3种方案容量配置结果可知,方案1至方案3中CHP、GSHP、ES和HS配置容量依次增加,而GB配置容量减少为0,电负荷需求从主要由外网购电转换为主要由系统CHP、PV、WT供电,热负荷需求则更多通过CHP和GSHP满足,减少了GB污染物排放量。总体来看,方案1倾向于低经济成本,而牺牲环境成本;方案3倾向于低环境成本,而经济成本增加较大;方案2是二者折中的一种方案。
针对第一阶段得到的3种规划方案,根据文中所设计的两阶段优化方法,第二阶段对各方案进行运行优化,从而得到典型日负荷供需平衡曲线,各方案运行成本如表3 所示。风电由于装机成本较高,故在方案1中并未配置风电,在供需平衡曲线中,方案1的电负荷主要以电网购电为主、PV发电以及ES为辅来完成供应,由于GSHP拥有较高的能量转换效率以及GB具有较低的安装成本,故热负荷主要由GSHP和GB供应。雄安地区风力资源中等,结合电负荷需求特性曲线,方案2和方案3均配置了400 kW的WT,由负荷供需平衡曲线可知,方案2电负荷主要由电网购电、WT、PV及CHP发电来供应,ES辅助调节;热负荷主要由GSHP、CHP机组供应,HS辅助调节。相比于方案1,方案2替换了经济成本较低、环境成本较高的GB,改用环境成本较低的CHP机组完成辅助供热。相比于方案2,方案3通过增加CHP、ES、HS的安装容量进一步降低环境成本,提升了系统利用清洁能源满足负荷供应的能力,在负荷供需平衡曲线中也可以看到系统减少了电网购电。
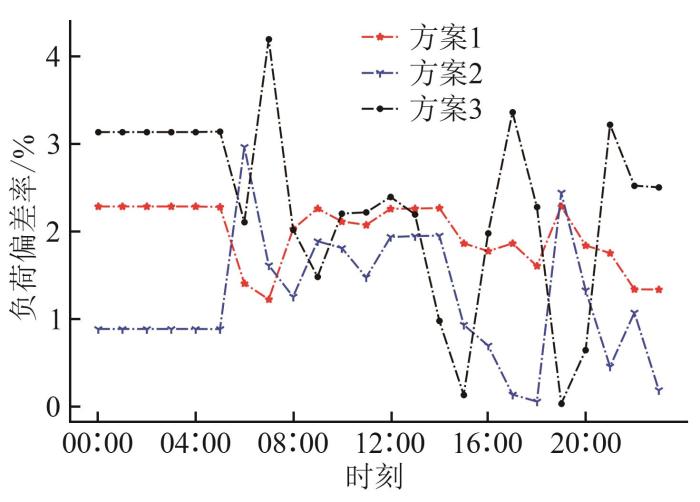
在第一、二阶段模型优化求解的基础上,进一步对各规划方案下系统运行时供能的可靠性进行评估,评估结果作为确定系统最佳规划方案的重要参考因素。针对3种规划方案,分别按照式(32)—(36)计算其典型日总负荷偏差率及其平均值,结果分别如图6 和表4 所示。对于方案1,其各设备的配置容量都偏低,难以满足负荷需求,故匹配程度较差,负荷偏差率较高;对于方案2和方案3,其偏差相较于方案1有大幅度降低,但依旧偏高,主要是系统为降低运行成本而低价购电、高价售电所致,由此可见,运行经济性与负荷偏差之间需要博弈均衡。相比于方案2,方案3由于设备配置容量过高,系统供能能力过剩,导致大量能源外售,进而引起偏差率较大。
图6
图6
不同规划方案典型日负荷偏差率
Fig. 6
Typical daily load deviation rate of different planning schemes
在上述分析基础上,为确定系统最佳规划方案,本文设计了方案综合评估指标C AI ,其计算公式为
C A I = [ ( f 1 + f 2 ) / 365 + f 3 ] × L R (38)
由式(38)可以看出,系统规划、运行成本越小,平均负荷偏差率越低,则C AI 值越小,方案越优;反之,则方案越差。按照式(38)计算方案1、方案2和方案3,其C AI 值分别为0.31、0.20和0.47,故选取方案2作为情景1下的最佳规划方案。
3.3 不同场景规划结果对比分析
利用本文提出的两阶段优化方法对场景2和场景3进行规划,求解过程与3.2中场景1类似,这里不再赘述。结合场景1中最佳规划方案(表2 中方案2),3种场景最佳规划方案容量配置情况如表5 所示。这3种场景中场景1经济成本和环境成本最低,这是由于场景1配置了较多的清洁能源设备,如PV、WT、GSHP,可以充分利用雄安地区光伏、风力、中深层地热等资源,减少了对外部购电、购气的依赖,提升系统经济性的同时也会大幅度降低污染物的排放;场景2主要通过CHP供电供热,由于配置了过多的HS,导致系统经济性降低,同时由于大量使用GB,导致系统排放大量污染物,从而增加了环境成本;场景3配置了大量EB,EB相对于GSHP不仅能量转换效率低,而且耗电量较高,污染物排放量大,同时由于缺少HS辅助调节,系统灵活性较差。
同时,对3种场景最佳规划方案对应的运行情况进行对比分析,3种场景典型日运行成本对比情况如表6 所示。由负荷供需平衡曲线可知,场景2电负荷主要以电网购电为主、CHP和PV发电为辅来满足,系统电交易成本较高,热负荷主要以CHP供热为主、GB为辅来满足,同时利用HS辅助调节,由于未利用地热资源和GSHP,导致经济成本和环境成本均较高。场景3电负荷主要由电网购电、CHP和PV发电来满足,并利用一定容量的ES来辅助调节,其热负荷主要由CHP和EB来供热,EB耗电且转换效率低,导致系统总运行成本较高。
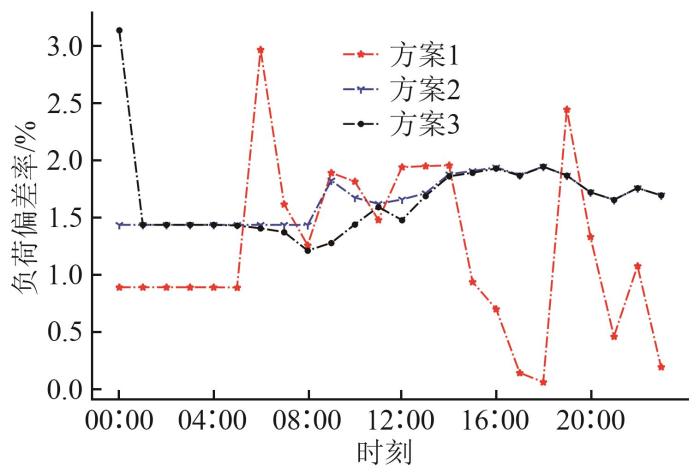
除经济性和环保性之外,对3种场景最佳规划方案负荷供给的可靠性进行对比,典型日负荷偏差率及其平均值分别如图7 和表7 所示。场景1配有储能设备,且供电、供热设备种类丰富,系统具有较好的灵活性;场景2电负荷主要由电网购电和CHP发电来满足,能量来源较为单一,对于尖峰负荷只能依靠外部电网来补充,负荷偏差率增大;对于场景3,虽然ES的增加可以实现系统电能调节,但是其低储高放的运行特性又会导致负荷偏差率进一步升高。
图7
图7
不同场景最佳规划方案典型日负荷偏差率
Fig. 7
Typical daily load deviation rate of the best planning scheme in different scenarios
4 结论
1)充分考虑地区可利用资源形式,构建了园区供暖期供能结构,在满足用户用能需求的同时兼顾了系统灵活性和经济性。
2)构建了计及负荷供给可靠性的CIES两阶段规划优化模型,该模型同时考虑系统运行的经济性、环保性和负荷供给的可靠性,使得规划结果更加符合实际情况。
3)提出采用带精英保留策略的NSGA-II算法对CIES两阶段规划优化模型进行求解,通过对多个场景进行规划及结果对比分析,验证了所提规划方法及流程的可行性,适用于求解CIES的容量优化配置问题。
参考文献
View Option
[1]
BAO Z ZHOU Q YANG Z et al A multi time-scale and multi energy-type co-ordinated microgrid scheduling solution—part I:model and methodology
[J].IEEE Transactions on Power Systems ,2015 ,30 (5 ):2257 -2266 . doi:10.1109/tpwrs.2014.2367127
[本文引用: 1]
[2]
施锦月 ,许健 ,曾博 ,等 基于热电比可调模式的区域综合能源系统双层优化运行
[J].电网技术 ,2016 ,40 (10 ):2959 -2966 .
SHI J Y XU J ZENG B et al A bi-level optimal operation for energy hub based on regulating heat-to-electric ratio mode
[J].Power System Technology ,2016 ,40 (10 ):2959 -2966 .
[3]
HUANG Y Z ZHOU Y H ZHENG G W et al Research on new integrated energy system with multi-power combined supply of industrial parks
[J].Power Generation Technology ,2021 ,42 (6 ):734 -740 . doi:10.12096/j.2096-4528.pgt.21099
[5]
[本文引用: 1]
JIA H J WANG D XU X D et al Research on some key problems related to integrated energy systems
[J].Automation of Electric Power Systems ,2015 ,39 (7 ):198 -207 . doi:10.7500/AEPS20141009011
[本文引用: 1]
[6]
郝然 ,艾芊 ,朱宇超 ,等 基于能源集线器的区域综合能源系统分层优化调度
[J].电力自动化设备 ,2017 ,37 (6 ):171 -178 .
HAO R AI Q ZHU Y C et al Hierarchical optimal dispatch based on energy hub for regional integrated energy system
[J].Electric Power Automation Equipment ,2017 ,37 (6 ):171 -178 .
[7]
汪飞 ,龚丹丹 ,郭慧 ,等 计及动态氢价和不确定性的区域综合能源系统规划-运行两阶段优化
[J].电力系统保护与控制 ,2022 ,50 (13 ):53 -62 .
WANG F GONG D D GUO H et al Two-stage optimization of regional integrated energy system planning-operation with dynamic hydrogen pricing and uncertainties
[J].Power System Protection and Control ,2022 ,50 (13 ):53 -62 .
[8]
[本文引用: 1]
ZHAO E M ZHANG B LI H Z et al Economic benefit evaluation of regional integrated energy system based on improved minimum cross entropy method
[J].Electric Power Engineering Technology ,2022 ,41 (2 ):215 -223 . doi:10.12158/j.2096-3203.2022.02.029
[本文引用: 1]
[9]
QUELHAS A GIL E MCCALLEY J D et al A multiperiod generalized network flow model of the U.S. integrated energy system—part I:model description
[J]. IEEE Transactions on Power Systems , 2007 ,22 (2 ):829 -836 . doi:10.1109/tpwrs.2007.894844
[本文引用: 1]
[10]
LIU C SHAHIDEHPOUR M FU Y et al Security-constrained unit commitment with natural gas transmission constraints
[J].IEEE Transactions on Power Systems ,2009 ,24 (3 ):1523 -1536 . doi:10.1109/tpwrs.2009.2023262
[本文引用: 1]
[11]
[本文引用: 1]
ZHOU C C MA X Y GUO X B et al Leader-follower game based optimized operation method for interaction of integrated energy system in industrial park
[J].Automation of Electric Power Systems , 2019 , 43 (7 ):74 -80 . doi:10.7500/AEPS20180604007
[本文引用: 1]
[12]
赵瑾 ,雍静 ,郇嘉嘉 ,等 基于长时间尺度的园区综合能源系统随机规划
[J].电力自动化设备 ,2020 ,40 (3 ):68 -73 .
ZHAO J YONG J HUAN J J et al Stochastic planning of park-level integrated energy system based on long time-scale
[J].Electric Power Automation Equipment ,2020 ,40 (3 ):68 -73 .
[14]
XUE Y GAO Y LI Y et al Optimal coordinated operation of electricity and natural gas distribution networks with power-to-gas facilities
[C]//2018 IEEE Innovative Smart Grid Technologies-Asia (ISGTAsia) .Singapore ,IEEE ,2018 :294 -299 . doi:10.1109/isgt-asia.2018.8467790
[本文引用: 1]
[15]
SALIMI M GHASEMI H ADELPOUR M et al Optimal planning of energy hubs in interconnected energy systems:a case study for natural gas and electricity
[J].IET Generation,Transmission & Distribution ,2015 ,9 (8 ):695 -707 . doi:10.1049/iet-gtd.2014.0607
[本文引用: 1]
[16]
刘迪 ,吴俊勇 ,林凯骏 ,等 基于 Kriging 模型的综合能源系统规划方法
[J].电网技术 ,2019 ,43 (1 ):185 -194 .
[本文引用: 2]
LIU D WU J Y LIN K J et al Comprehensive energy system planning method based on Kriging model
[J]. Power System Technology ,2019 ,43 (1 ):185 -194 .
[本文引用: 2]
[17]
[本文引用: 1]
HUANG W LIU W B Multi-energy complementary based coordinated optimal planning of park integrated energy station-network
[J].Automation of Electric Power Systems ,2020 ,44 (23 ):20 -28 . doi:10.7500/AEPS20200424002
[本文引用: 1]
[18]
[本文引用: 1]
HUANG W LIU S Q YE B Station-network cooperative optimization of integrated energy system for park considering source-load interaction
[J]. Automation of Electric Power Systems ,2020 , 44 (14 ):44 -53 . doi:10.7500/AEPS20190521003
[本文引用: 1]
[19]
范宏 ,袁倩倩 ,邓剑 多区域综合能源系统的两阶段容量优化配置方法
[J].现代电力 ,2020 ,37 (5 ): 441 -447 .
[本文引用: 1]
FAN H YUAN Q Q DENG J A two-stage optimal capacity configuration of multi-region integrated energy system
[J].Modern Electric Power ,2020 ,37 (5 ):441 -447 .
[本文引用: 1]
[20]
DEB K PRATAP A AGARWAL S et al A fast and elitist multiobjective genetic algorithm:NSGA-Ⅱ
[J].IEEE Transactions on Evolutionary Computation ,2002 ,6 (2 ):182 -197 . doi:10.1109/4235.996017
[本文引用: 1]
[21]
VIANA A PEDROSO J P A new MILP-based approach for unit commitment in power production planning
[J].International Journal of Electrical Power & Energy Systems ,2013 ,44 (1 ):997 -1005 . doi:10.1016/j.ijepes.2012.08.046
[本文引用: 1]
A multi time-scale and multi energy-type co-ordinated microgrid scheduling solution—part I:model and methodology
1
2015
... 随着“2030年碳达峰、2060年碳中和”能源发展目标的提出,能源转型加速推进,综合能源系统因其在促进清洁能源消纳、提升能源利用率和降低用能成本方面的显著作用,已成为满足多能供需的新的能源利用实现方式.从地理范围上讲,综合能源系统可以划分为局域级[1 -4 ] (如楼宇、社区、工厂等)、区域级[5 -8 ] (如城区)和广域级[9 -10 ] (如城市、跨区域、跨国等).园区综合能源系统(community integrated energy system,CIES)[11 -13 ] 作为典型的局域级综合能源系统,通过建立电力、天然气、可再生能源等多种能源之间的耦合利用关系,可以显著提高能源综合利用效率、降低用能成本和减少碳排放量,为实现低碳园区建设提供了一种有效途径.因此,开展CIES规划研究具有重要意义. ...
基于热电比可调模式的区域综合能源系统双层优化运行
0
2016
基于热电比可调模式的区域综合能源系统双层优化运行
0
2016
产业园区新型多能联供综合能源服务研究
0
2021
产业园区新型多能联供综合能源服务研究
0
2021
考虑生物质供给价格弹性的工业园区综合能源系统规划
1
2021
... 随着“2030年碳达峰、2060年碳中和”能源发展目标的提出,能源转型加速推进,综合能源系统因其在促进清洁能源消纳、提升能源利用率和降低用能成本方面的显著作用,已成为满足多能供需的新的能源利用实现方式.从地理范围上讲,综合能源系统可以划分为局域级[1 -4 ] (如楼宇、社区、工厂等)、区域级[5 -8 ] (如城区)和广域级[9 -10 ] (如城市、跨区域、跨国等).园区综合能源系统(community integrated energy system,CIES)[11 -13 ] 作为典型的局域级综合能源系统,通过建立电力、天然气、可再生能源等多种能源之间的耦合利用关系,可以显著提高能源综合利用效率、降低用能成本和减少碳排放量,为实现低碳园区建设提供了一种有效途径.因此,开展CIES规划研究具有重要意义. ...
考虑生物质供给价格弹性的工业园区综合能源系统规划
1
2021
... 随着“2030年碳达峰、2060年碳中和”能源发展目标的提出,能源转型加速推进,综合能源系统因其在促进清洁能源消纳、提升能源利用率和降低用能成本方面的显著作用,已成为满足多能供需的新的能源利用实现方式.从地理范围上讲,综合能源系统可以划分为局域级[1 -4 ] (如楼宇、社区、工厂等)、区域级[5 -8 ] (如城区)和广域级[9 -10 ] (如城市、跨区域、跨国等).园区综合能源系统(community integrated energy system,CIES)[11 -13 ] 作为典型的局域级综合能源系统,通过建立电力、天然气、可再生能源等多种能源之间的耦合利用关系,可以显著提高能源综合利用效率、降低用能成本和减少碳排放量,为实现低碳园区建设提供了一种有效途径.因此,开展CIES规划研究具有重要意义. ...
区域综合能源系统若干问题研究
1
2015
... 随着“2030年碳达峰、2060年碳中和”能源发展目标的提出,能源转型加速推进,综合能源系统因其在促进清洁能源消纳、提升能源利用率和降低用能成本方面的显著作用,已成为满足多能供需的新的能源利用实现方式.从地理范围上讲,综合能源系统可以划分为局域级[1 -4 ] (如楼宇、社区、工厂等)、区域级[5 -8 ] (如城区)和广域级[9 -10 ] (如城市、跨区域、跨国等).园区综合能源系统(community integrated energy system,CIES)[11 -13 ] 作为典型的局域级综合能源系统,通过建立电力、天然气、可再生能源等多种能源之间的耦合利用关系,可以显著提高能源综合利用效率、降低用能成本和减少碳排放量,为实现低碳园区建设提供了一种有效途径.因此,开展CIES规划研究具有重要意义. ...
区域综合能源系统若干问题研究
1
2015
... 随着“2030年碳达峰、2060年碳中和”能源发展目标的提出,能源转型加速推进,综合能源系统因其在促进清洁能源消纳、提升能源利用率和降低用能成本方面的显著作用,已成为满足多能供需的新的能源利用实现方式.从地理范围上讲,综合能源系统可以划分为局域级[1 -4 ] (如楼宇、社区、工厂等)、区域级[5 -8 ] (如城区)和广域级[9 -10 ] (如城市、跨区域、跨国等).园区综合能源系统(community integrated energy system,CIES)[11 -13 ] 作为典型的局域级综合能源系统,通过建立电力、天然气、可再生能源等多种能源之间的耦合利用关系,可以显著提高能源综合利用效率、降低用能成本和减少碳排放量,为实现低碳园区建设提供了一种有效途径.因此,开展CIES规划研究具有重要意义. ...
基于能源集线器的区域综合能源系统分层优化调度
0
2017
基于能源集线器的区域综合能源系统分层优化调度
0
2017
计及动态氢价和不确定性的区域综合能源系统规划-运行两阶段优化
0
2022
计及动态氢价和不确定性的区域综合能源系统规划-运行两阶段优化
0
2022
基于改进最小叉熵法的区域综合能源系统经济效益评估
1
2022
... 随着“2030年碳达峰、2060年碳中和”能源发展目标的提出,能源转型加速推进,综合能源系统因其在促进清洁能源消纳、提升能源利用率和降低用能成本方面的显著作用,已成为满足多能供需的新的能源利用实现方式.从地理范围上讲,综合能源系统可以划分为局域级[1 -4 ] (如楼宇、社区、工厂等)、区域级[5 -8 ] (如城区)和广域级[9 -10 ] (如城市、跨区域、跨国等).园区综合能源系统(community integrated energy system,CIES)[11 -13 ] 作为典型的局域级综合能源系统,通过建立电力、天然气、可再生能源等多种能源之间的耦合利用关系,可以显著提高能源综合利用效率、降低用能成本和减少碳排放量,为实现低碳园区建设提供了一种有效途径.因此,开展CIES规划研究具有重要意义. ...
基于改进最小叉熵法的区域综合能源系统经济效益评估
1
2022
... 随着“2030年碳达峰、2060年碳中和”能源发展目标的提出,能源转型加速推进,综合能源系统因其在促进清洁能源消纳、提升能源利用率和降低用能成本方面的显著作用,已成为满足多能供需的新的能源利用实现方式.从地理范围上讲,综合能源系统可以划分为局域级[1 -4 ] (如楼宇、社区、工厂等)、区域级[5 -8 ] (如城区)和广域级[9 -10 ] (如城市、跨区域、跨国等).园区综合能源系统(community integrated energy system,CIES)[11 -13 ] 作为典型的局域级综合能源系统,通过建立电力、天然气、可再生能源等多种能源之间的耦合利用关系,可以显著提高能源综合利用效率、降低用能成本和减少碳排放量,为实现低碳园区建设提供了一种有效途径.因此,开展CIES规划研究具有重要意义. ...
A multiperiod generalized network flow model of the U.S. integrated energy system—part I:model description
1
2007
... 随着“2030年碳达峰、2060年碳中和”能源发展目标的提出,能源转型加速推进,综合能源系统因其在促进清洁能源消纳、提升能源利用率和降低用能成本方面的显著作用,已成为满足多能供需的新的能源利用实现方式.从地理范围上讲,综合能源系统可以划分为局域级[1 -4 ] (如楼宇、社区、工厂等)、区域级[5 -8 ] (如城区)和广域级[9 -10 ] (如城市、跨区域、跨国等).园区综合能源系统(community integrated energy system,CIES)[11 -13 ] 作为典型的局域级综合能源系统,通过建立电力、天然气、可再生能源等多种能源之间的耦合利用关系,可以显著提高能源综合利用效率、降低用能成本和减少碳排放量,为实现低碳园区建设提供了一种有效途径.因此,开展CIES规划研究具有重要意义. ...
Security-constrained unit commitment with natural gas transmission constraints
1
2009
... 随着“2030年碳达峰、2060年碳中和”能源发展目标的提出,能源转型加速推进,综合能源系统因其在促进清洁能源消纳、提升能源利用率和降低用能成本方面的显著作用,已成为满足多能供需的新的能源利用实现方式.从地理范围上讲,综合能源系统可以划分为局域级[1 -4 ] (如楼宇、社区、工厂等)、区域级[5 -8 ] (如城区)和广域级[9 -10 ] (如城市、跨区域、跨国等).园区综合能源系统(community integrated energy system,CIES)[11 -13 ] 作为典型的局域级综合能源系统,通过建立电力、天然气、可再生能源等多种能源之间的耦合利用关系,可以显著提高能源综合利用效率、降低用能成本和减少碳排放量,为实现低碳园区建设提供了一种有效途径.因此,开展CIES规划研究具有重要意义. ...
基于主从博弈的工业园区综合能源系统互动优化运行方法
1
2019
... 随着“2030年碳达峰、2060年碳中和”能源发展目标的提出,能源转型加速推进,综合能源系统因其在促进清洁能源消纳、提升能源利用率和降低用能成本方面的显著作用,已成为满足多能供需的新的能源利用实现方式.从地理范围上讲,综合能源系统可以划分为局域级[1 -4 ] (如楼宇、社区、工厂等)、区域级[5 -8 ] (如城区)和广域级[9 -10 ] (如城市、跨区域、跨国等).园区综合能源系统(community integrated energy system,CIES)[11 -13 ] 作为典型的局域级综合能源系统,通过建立电力、天然气、可再生能源等多种能源之间的耦合利用关系,可以显著提高能源综合利用效率、降低用能成本和减少碳排放量,为实现低碳园区建设提供了一种有效途径.因此,开展CIES规划研究具有重要意义. ...
基于主从博弈的工业园区综合能源系统互动优化运行方法
1
2019
... 随着“2030年碳达峰、2060年碳中和”能源发展目标的提出,能源转型加速推进,综合能源系统因其在促进清洁能源消纳、提升能源利用率和降低用能成本方面的显著作用,已成为满足多能供需的新的能源利用实现方式.从地理范围上讲,综合能源系统可以划分为局域级[1 -4 ] (如楼宇、社区、工厂等)、区域级[5 -8 ] (如城区)和广域级[9 -10 ] (如城市、跨区域、跨国等).园区综合能源系统(community integrated energy system,CIES)[11 -13 ] 作为典型的局域级综合能源系统,通过建立电力、天然气、可再生能源等多种能源之间的耦合利用关系,可以显著提高能源综合利用效率、降低用能成本和减少碳排放量,为实现低碳园区建设提供了一种有效途径.因此,开展CIES规划研究具有重要意义. ...
基于长时间尺度的园区综合能源系统随机规划
0
2020
基于长时间尺度的园区综合能源系统随机规划
0
2020
考虑需求侧响应的园区综合能源系统优化配置
1
2020
... 随着“2030年碳达峰、2060年碳中和”能源发展目标的提出,能源转型加速推进,综合能源系统因其在促进清洁能源消纳、提升能源利用率和降低用能成本方面的显著作用,已成为满足多能供需的新的能源利用实现方式.从地理范围上讲,综合能源系统可以划分为局域级[1 -4 ] (如楼宇、社区、工厂等)、区域级[5 -8 ] (如城区)和广域级[9 -10 ] (如城市、跨区域、跨国等).园区综合能源系统(community integrated energy system,CIES)[11 -13 ] 作为典型的局域级综合能源系统,通过建立电力、天然气、可再生能源等多种能源之间的耦合利用关系,可以显著提高能源综合利用效率、降低用能成本和减少碳排放量,为实现低碳园区建设提供了一种有效途径.因此,开展CIES规划研究具有重要意义. ...
考虑需求侧响应的园区综合能源系统优化配置
1
2020
... 随着“2030年碳达峰、2060年碳中和”能源发展目标的提出,能源转型加速推进,综合能源系统因其在促进清洁能源消纳、提升能源利用率和降低用能成本方面的显著作用,已成为满足多能供需的新的能源利用实现方式.从地理范围上讲,综合能源系统可以划分为局域级[1 -4 ] (如楼宇、社区、工厂等)、区域级[5 -8 ] (如城区)和广域级[9 -10 ] (如城市、跨区域、跨国等).园区综合能源系统(community integrated energy system,CIES)[11 -13 ] 作为典型的局域级综合能源系统,通过建立电力、天然气、可再生能源等多种能源之间的耦合利用关系,可以显著提高能源综合利用效率、降低用能成本和减少碳排放量,为实现低碳园区建设提供了一种有效途径.因此,开展CIES规划研究具有重要意义. ...
Optimal coordinated operation of electricity and natural gas distribution networks with power-to-gas facilities
1
2018
... 现有CIES规划的研究主要集中于能源站内设备选型和定容,大致可以划分为2个阶段.第一个阶段为单纯的规划模型优化研究阶段,如:文献[14 ]中以电-气综合能源系统作为研究对象,通过建立电气耦合模型优化得到能源站容量配置;文献[15 ]中同时对多个能源站进行规划,充分考虑能源站内不同形式能源耦合和不同能源站间的互联关系,优化得到各能源站的容量配置;文献[16 ]中建立了综合能源系统主要设备的能量流模型,并在此基础上利用改进Kriging模型对系统进行规划优化,计算得到系统最佳规划方案等.以上文献虽对综合能源系统进行规划,但都是只考虑系统的规划优化,未涉及系统运行优化. ...
Optimal planning of energy hubs in interconnected energy systems:a case study for natural gas and electricity
1
2015
... 现有CIES规划的研究主要集中于能源站内设备选型和定容,大致可以划分为2个阶段.第一个阶段为单纯的规划模型优化研究阶段,如:文献[14 ]中以电-气综合能源系统作为研究对象,通过建立电气耦合模型优化得到能源站容量配置;文献[15 ]中同时对多个能源站进行规划,充分考虑能源站内不同形式能源耦合和不同能源站间的互联关系,优化得到各能源站的容量配置;文献[16 ]中建立了综合能源系统主要设备的能量流模型,并在此基础上利用改进Kriging模型对系统进行规划优化,计算得到系统最佳规划方案等.以上文献虽对综合能源系统进行规划,但都是只考虑系统的规划优化,未涉及系统运行优化. ...
基于 Kriging 模型的综合能源系统规划方法
2
2019
... 现有CIES规划的研究主要集中于能源站内设备选型和定容,大致可以划分为2个阶段.第一个阶段为单纯的规划模型优化研究阶段,如:文献[14 ]中以电-气综合能源系统作为研究对象,通过建立电气耦合模型优化得到能源站容量配置;文献[15 ]中同时对多个能源站进行规划,充分考虑能源站内不同形式能源耦合和不同能源站间的互联关系,优化得到各能源站的容量配置;文献[16 ]中建立了综合能源系统主要设备的能量流模型,并在此基础上利用改进Kriging模型对系统进行规划优化,计算得到系统最佳规划方案等.以上文献虽对综合能源系统进行规划,但都是只考虑系统的规划优化,未涉及系统运行优化. ...
... 第二个阶段为协同规划优化研究阶段,在进行规划的同时考虑系统运行经济性、环保性等,使得规划的结果更具实用性,如:文献[17 ]考虑站-网协同,构建了CIES双层规划优化模型,上层规划求解能源站数量、位置和容量,下层通过建立多能源站规划运行联合优化模型对系统运行进行优化,优化结果返回上层进行更新;文献[18 ]考虑源-荷互动,建立了CIES站-网协同双层规划优化模型,规划结果相较于文献[16 ]更加经济合理;文献[19 ]对多区域综合能源系统规划进行研究,提出了一种两阶段优化方法,通过优化系统的经济和环境成本求解各区域能源容量配置.上述文献在进行系统规划的同时考虑了系统运行优化,但也存在一定的局限性,如规划模型建模普遍简单,为单目标优化问题;系统供能结构单一,候选设备类型较少;普遍只考虑了系统运行时的经济性和环保性,而对于系统运行时的其他重要因素(如负荷供给可靠性)考虑较少等. ...
基于 Kriging 模型的综合能源系统规划方法
2
2019
... 现有CIES规划的研究主要集中于能源站内设备选型和定容,大致可以划分为2个阶段.第一个阶段为单纯的规划模型优化研究阶段,如:文献[14 ]中以电-气综合能源系统作为研究对象,通过建立电气耦合模型优化得到能源站容量配置;文献[15 ]中同时对多个能源站进行规划,充分考虑能源站内不同形式能源耦合和不同能源站间的互联关系,优化得到各能源站的容量配置;文献[16 ]中建立了综合能源系统主要设备的能量流模型,并在此基础上利用改进Kriging模型对系统进行规划优化,计算得到系统最佳规划方案等.以上文献虽对综合能源系统进行规划,但都是只考虑系统的规划优化,未涉及系统运行优化. ...
... 第二个阶段为协同规划优化研究阶段,在进行规划的同时考虑系统运行经济性、环保性等,使得规划的结果更具实用性,如:文献[17 ]考虑站-网协同,构建了CIES双层规划优化模型,上层规划求解能源站数量、位置和容量,下层通过建立多能源站规划运行联合优化模型对系统运行进行优化,优化结果返回上层进行更新;文献[18 ]考虑源-荷互动,建立了CIES站-网协同双层规划优化模型,规划结果相较于文献[16 ]更加经济合理;文献[19 ]对多区域综合能源系统规划进行研究,提出了一种两阶段优化方法,通过优化系统的经济和环境成本求解各区域能源容量配置.上述文献在进行系统规划的同时考虑了系统运行优化,但也存在一定的局限性,如规划模型建模普遍简单,为单目标优化问题;系统供能结构单一,候选设备类型较少;普遍只考虑了系统运行时的经济性和环保性,而对于系统运行时的其他重要因素(如负荷供给可靠性)考虑较少等. ...
基于多能互补的园区综合能源站-网协同优化规划
1
2020
... 第二个阶段为协同规划优化研究阶段,在进行规划的同时考虑系统运行经济性、环保性等,使得规划的结果更具实用性,如:文献[17 ]考虑站-网协同,构建了CIES双层规划优化模型,上层规划求解能源站数量、位置和容量,下层通过建立多能源站规划运行联合优化模型对系统运行进行优化,优化结果返回上层进行更新;文献[18 ]考虑源-荷互动,建立了CIES站-网协同双层规划优化模型,规划结果相较于文献[16 ]更加经济合理;文献[19 ]对多区域综合能源系统规划进行研究,提出了一种两阶段优化方法,通过优化系统的经济和环境成本求解各区域能源容量配置.上述文献在进行系统规划的同时考虑了系统运行优化,但也存在一定的局限性,如规划模型建模普遍简单,为单目标优化问题;系统供能结构单一,候选设备类型较少;普遍只考虑了系统运行时的经济性和环保性,而对于系统运行时的其他重要因素(如负荷供给可靠性)考虑较少等. ...
基于多能互补的园区综合能源站-网协同优化规划
1
2020
... 第二个阶段为协同规划优化研究阶段,在进行规划的同时考虑系统运行经济性、环保性等,使得规划的结果更具实用性,如:文献[17 ]考虑站-网协同,构建了CIES双层规划优化模型,上层规划求解能源站数量、位置和容量,下层通过建立多能源站规划运行联合优化模型对系统运行进行优化,优化结果返回上层进行更新;文献[18 ]考虑源-荷互动,建立了CIES站-网协同双层规划优化模型,规划结果相较于文献[16 ]更加经济合理;文献[19 ]对多区域综合能源系统规划进行研究,提出了一种两阶段优化方法,通过优化系统的经济和环境成本求解各区域能源容量配置.上述文献在进行系统规划的同时考虑了系统运行优化,但也存在一定的局限性,如规划模型建模普遍简单,为单目标优化问题;系统供能结构单一,候选设备类型较少;普遍只考虑了系统运行时的经济性和环保性,而对于系统运行时的其他重要因素(如负荷供给可靠性)考虑较少等. ...
考虑源-荷互动的园区综合能源系统站-网协同优化
1
2020
... 第二个阶段为协同规划优化研究阶段,在进行规划的同时考虑系统运行经济性、环保性等,使得规划的结果更具实用性,如:文献[17 ]考虑站-网协同,构建了CIES双层规划优化模型,上层规划求解能源站数量、位置和容量,下层通过建立多能源站规划运行联合优化模型对系统运行进行优化,优化结果返回上层进行更新;文献[18 ]考虑源-荷互动,建立了CIES站-网协同双层规划优化模型,规划结果相较于文献[16 ]更加经济合理;文献[19 ]对多区域综合能源系统规划进行研究,提出了一种两阶段优化方法,通过优化系统的经济和环境成本求解各区域能源容量配置.上述文献在进行系统规划的同时考虑了系统运行优化,但也存在一定的局限性,如规划模型建模普遍简单,为单目标优化问题;系统供能结构单一,候选设备类型较少;普遍只考虑了系统运行时的经济性和环保性,而对于系统运行时的其他重要因素(如负荷供给可靠性)考虑较少等. ...
考虑源-荷互动的园区综合能源系统站-网协同优化
1
2020
... 第二个阶段为协同规划优化研究阶段,在进行规划的同时考虑系统运行经济性、环保性等,使得规划的结果更具实用性,如:文献[17 ]考虑站-网协同,构建了CIES双层规划优化模型,上层规划求解能源站数量、位置和容量,下层通过建立多能源站规划运行联合优化模型对系统运行进行优化,优化结果返回上层进行更新;文献[18 ]考虑源-荷互动,建立了CIES站-网协同双层规划优化模型,规划结果相较于文献[16 ]更加经济合理;文献[19 ]对多区域综合能源系统规划进行研究,提出了一种两阶段优化方法,通过优化系统的经济和环境成本求解各区域能源容量配置.上述文献在进行系统规划的同时考虑了系统运行优化,但也存在一定的局限性,如规划模型建模普遍简单,为单目标优化问题;系统供能结构单一,候选设备类型较少;普遍只考虑了系统运行时的经济性和环保性,而对于系统运行时的其他重要因素(如负荷供给可靠性)考虑较少等. ...
多区域综合能源系统的两阶段容量优化配置方法
1
2020
... 第二个阶段为协同规划优化研究阶段,在进行规划的同时考虑系统运行经济性、环保性等,使得规划的结果更具实用性,如:文献[17 ]考虑站-网协同,构建了CIES双层规划优化模型,上层规划求解能源站数量、位置和容量,下层通过建立多能源站规划运行联合优化模型对系统运行进行优化,优化结果返回上层进行更新;文献[18 ]考虑源-荷互动,建立了CIES站-网协同双层规划优化模型,规划结果相较于文献[16 ]更加经济合理;文献[19 ]对多区域综合能源系统规划进行研究,提出了一种两阶段优化方法,通过优化系统的经济和环境成本求解各区域能源容量配置.上述文献在进行系统规划的同时考虑了系统运行优化,但也存在一定的局限性,如规划模型建模普遍简单,为单目标优化问题;系统供能结构单一,候选设备类型较少;普遍只考虑了系统运行时的经济性和环保性,而对于系统运行时的其他重要因素(如负荷供给可靠性)考虑较少等. ...
多区域综合能源系统的两阶段容量优化配置方法
1
2020
... 第二个阶段为协同规划优化研究阶段,在进行规划的同时考虑系统运行经济性、环保性等,使得规划的结果更具实用性,如:文献[17 ]考虑站-网协同,构建了CIES双层规划优化模型,上层规划求解能源站数量、位置和容量,下层通过建立多能源站规划运行联合优化模型对系统运行进行优化,优化结果返回上层进行更新;文献[18 ]考虑源-荷互动,建立了CIES站-网协同双层规划优化模型,规划结果相较于文献[16 ]更加经济合理;文献[19 ]对多区域综合能源系统规划进行研究,提出了一种两阶段优化方法,通过优化系统的经济和环境成本求解各区域能源容量配置.上述文献在进行系统规划的同时考虑了系统运行优化,但也存在一定的局限性,如规划模型建模普遍简单,为单目标优化问题;系统供能结构单一,候选设备类型较少;普遍只考虑了系统运行时的经济性和环保性,而对于系统运行时的其他重要因素(如负荷供给可靠性)考虑较少等. ...
A fast and elitist multiobjective genetic algorithm:NSGA-Ⅱ
1
2002
... 第一阶段规划优化模型是多目标优化问题,目标函数分别为最小化年经济成本f 1 和最小化年环境成本f 2 ,可以直接通过Pareto最优解进行求解,而无需转化为单目标优化问题,避免了因目标函数合并不合理(如权重设置不合理等)而引起的计算误差.NSGA-II是一种基于Pareto最优解的多目标优化算法,对于难以求解的优化问题,通常仍能找到较优解且算法具有较好的收敛性[20 ] ,这里考虑带有精英保留策略的NSGA-II算法进行模型求解. ...
A new MILP-based approach for unit commitment in power production planning
1
2013
... 第一阶段规划模型求解通常会得到多组Pareto最优解,即多个规划方案,为确定最佳规划方案,第二阶段针对各组解(规划方案)开展系统运行优化分析,目标函数为最小化系统典型日运行、维护和污染物排放成本f 3 ,为单目标优化问题.考虑到约束条件中Nx 须为整数,因此第二阶段运行优化问题为典型的混合整数线性规划问题[21 ] ,决策变量为典型日各设备实时运行出力Px , t x 为该规划方案下系统运行设备,设其类别数为c ,t 表示01:00—24:00运行整点时刻,则该解可以表示为c ×24的矩阵 X f 3 . ...