模型旋流燃烧室气体燃料火焰不稳定特性分析

doi:10.12096/j.2096-4528.pgt.21093

模型旋流燃烧室气体燃料火焰不稳定特性分析

郝建刚¹, 贡文明², 丁阳¹, 郑丹伟³, 刘勇³

1.华电电力科学研究院有限公司，浙江省杭州市 310030

2.江苏华电戚墅堰发电有限公司，江苏省常州市 213011

3.航空发动机热环境与热结构工业和信息化部重点实验室(南京航空航天大学能源与动力学院)，江苏省南京市 210016

Analysis on Combustion Instability Characteristics of Model Swirl Combustor With Gas Fuel

HAO Jiangang¹, GONG Wenming², DING Yang¹, ZHENG Danwei³, LIU Yong³

1.Huadian Electric Power Research Institute Co. , Ltd. , Hangzhou 310030, Zhejiang Province, China

2.Jiangsu Huadian Qishuyan Power Generation Co. , Ltd. , Changzhou 213011, Jiangsu Province, China

3.Aero-engine Thermal Environment and Structure Key Laboratory of Ministry of Industry and Information Technology (College of Energy and Power Engineering, Nanjing University of Aeronautics and Astronautics), Nanjing 210016, Jiangsu Province, China

收稿日期: 2022-01-29

基金资助:

国家自然科学基金项目. 91741118

Received: 2022-01-29

作者简介 About authors

郝建刚(1983)，男，硕士，高级工程师，主要研究方向为火电厂经济运行，jiangang-hao@chder.com；

刘勇(1971)，男，博士，副教授，主要研究方向为燃烧理论和燃烧数值模拟，本文通信作者，LYYL71@nuaa.edu.cn。

摘要

燃机在贫燃工况下易出现燃烧不稳定，分析和预测不稳定燃烧特性对保证燃烧室正常工作具有重要意义。通过数值仿真得到燃烧室的火焰描述函数(flame describing function，FDF)，并结合低阶热声网络模型预测了燃烧室的热声不稳定特性。首先，通过模型旋流燃烧室自激振荡实验，得到振荡燃烧发生时的工况和主频；其次，利用大涡模拟(large eddy simulation，LES)，得到火焰燃烧热释放率对不同入口扰动的响应特征，通过拟合得到FDF；最后，建立了燃烧室低阶热声网络模型，并分析了燃烧室不稳定特性。结果表明：模型预测的振荡特性与实验数据相符，说明该模型能够从机理上预测燃烧不稳定特性。

关键词： 燃机燃烧室 ; 不稳定燃烧 ; 热声网络模型 ; 大涡模拟(LES) ; 火焰描述函数(FDF)

Abstract

Combustion instability is easy to occur under lean combustion of gas turbine. Analyzing and predicting the characteristics of unstable combustion is of great significance to ensure the normal operation of combustion chamber. The flame describing function (FDF) of combustion chamber was obtained by numerical simulation, and the thermoacoustic instability characteristics of combustion chamber were predicted by combining the low-order thermoacoustic network model. Firstly, the operating conditions and main frequency of oscillating combustion were obtained through the self-excited oscillation experiment of model swirler combustor.Secondly, by using large eddy simulation (LES), the response characteristics of heat release rate of flame combustion under different inlet disturbances were obtained, and the FDF was fitted. Finally, the low-order thermoacoustic network model of the combustion chamber was established, and the instability characteristics of the combustion chamber were analyzed. The results show that the oscillation characteristics predicted by the model are consistent with the experimental data, indicating that the model can predict the combustion instability characteristics from the mechanism.

Keywords： gas turbine combustor ; combustion instability ; thermoacoustic network model ; large eddy simulation (LES) ; flame describing function (FDF)

PDF (3128KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

郝建刚, 贡文明, 丁阳, 郑丹伟, 刘勇. 模型旋流燃烧室气体燃料火焰不稳定特性分析. 发电技术[J], 2022, 43(6): 927-934 DOI:10.12096/j.2096-4528.pgt.21093

HAO Jiangang, GONG Wenming, DING Yang, ZHENG Danwei, LIU Yong. Analysis on Combustion Instability Characteristics of Model Swirl Combustor With Gas Fuel. Power Generation Technology[J], 2022, 43(6): 927-934 DOI:10.12096/j.2096-4528.pgt.21093

0 引言

为了满足燃气轮机低污染物排放的要求，国内外众多机构和学者开展了多种低污染燃烧技术研究^[1-2]。然而低污染燃烧技术在显著降低NO _x 等排放量的同时，由于通常工作在贫燃状态下，也带来了燃烧不稳定等问题。在某些工况下，燃烧室释热率脉动与声压脉动发生耦合，当二者相位满足瑞利准则^[3]时，系统可能发生不稳定燃烧。不稳定燃烧一旦发生，就有可能产生燃烧振荡，强大的压力脉动将影响燃机运行效率，严重时大幅低频压力振荡对系统造成损害，威胁运行安全。

近年来，针对燃烧室不稳定燃烧现象，众多学者开展了关于不稳定燃烧特性的实验研究^[4-6]，并在此基础上发展了预测技术，这对于保证燃烧室在较宽的工作范围内正常工作具有重要意义。在不稳定燃烧特性的预测方法上，除了简单的代数模型外，大致分为2个思路：基于计算流体力学(computational fluid dynamics，CFD)的数值模拟预测方法和低阶热声网络(low-order thermoacoustic network，LOTAN)模型方法。数值模拟的方法能够模拟出不稳定燃烧的细节，近年来在机理研究方面取得了许多进展^[7-8]。但将其作为一种预测手段时，由于燃气轮机燃烧室结构复杂，而数值模拟需要对整个燃机燃烧室进行建模，计算求解对计算机性能要求较高，因此可行性较差。LOTAN模型从热声耦合出发，将燃烧系统简化为若干个相连的声学单元，火焰的非稳态过程通过火焰对声学扰动的不稳定热释放响应模型进行描述，从而实现了系统声学与非稳态的热释放过程的解耦。因此，LOTAN模型兼顾了不稳定燃烧预测的经济性与准确性。

常见的火焰响应模型有火焰传递函数(flame transfer function，FTF)和火焰描述函数(flame describing function，FDF)。FTF能够表征火焰释热率脉动随火焰锋面位置速度脉动的线性变化过程，传统的FTF模型有n-τ模型^[9]，以及在此基础上发展出来的带有一阶滤波的n-τ模型^[10-11]等。然而，线性FTF的适用范围仅限于微弱线性扰动，对于大多数火焰对流动扰动具有的非线性响应^[12-13]，FTF通常难以直接进行捕捉。但线性FTF仍然提供了许多有用信息(如预测线性不稳定边界)，为了将线性FTF的结果拓展至非线性区域，学者们提出了FDF的概念。相关研究^[14-17]结果表明：FDF不仅适用于实验室规模燃烧器，还适用于高压运行的实际燃气轮机燃烧室。FTF可通过理论分析、数值计算和实验测量等方法获得。Balachandran等^[18]通过自由基化学发光法测量放热率及平面激光诱导荧光成像法挖掘了FTF的非线性规律。Thumuluru等^[19]基于旋流稳燃FTF的饱和机理，确定了饱和过程的主要影响因素。Noiray等^[20]研究表明：激励振幅的相位变化，进而引起驱动燃烧不稳定产生的瑞利源项的改变，是导致FDF饱和的主要原因。于丹等^[21]通过实验的方法研究了不同当量比及空气流量对自激振荡模态下的分布式FTF相位分布的影响，结果表明，涡环形成所造成的相位增量是研究燃烧不稳定性的关键因素。翁方龙等^[22]针对火焰动力学的非线性特征，在FTF基础上，通过声学网络模型分析，提出针对含火焰动力学过程的解耦测量方法，并开展FDF实验测量与仿真分析验证。Han等^[23]通过大涡模拟(large eddy simulation，LES)方法，研究了进口声学扰动下部分预混火焰的FDF特征，随后采用LOTAN模型进一步研究了燃烧不稳定特性，特别是火焰的极限环频率和振幅等非线性特征。付虓等^[24]通过实验的方法获得了值班模型燃烧室中值班火焰的FTF，并利用延迟时间定量地描述了值班火焰的动态特征。

利用LOTAN模型法预测系统的不稳定燃烧特性，首先需要确定合适的火焰模型，用于描述火焰行为，然而目前对旋流扩散火焰的响应特征研究还不足，难以建立一个合理的预测模型。为此，本文以丙烷旋流扩散火焰为研究对象，通过实验研究了模型旋流燃烧室振荡燃烧发生时的工况和主频，采用LES方法建立了不稳定释热率对入口速度扰动的响应特征，在此仿真数据的基础上获得FDF，并结合LOTAN模型进行振荡燃烧特性的预测。

1 实验与测量系统

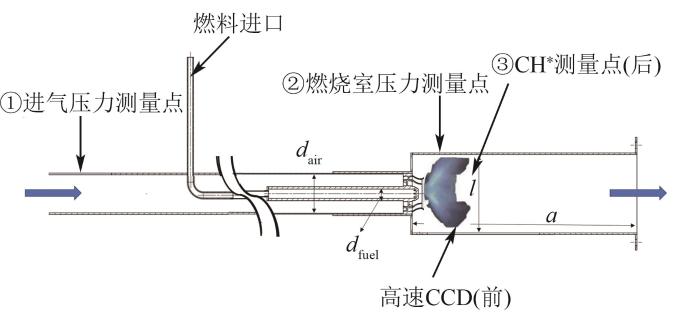
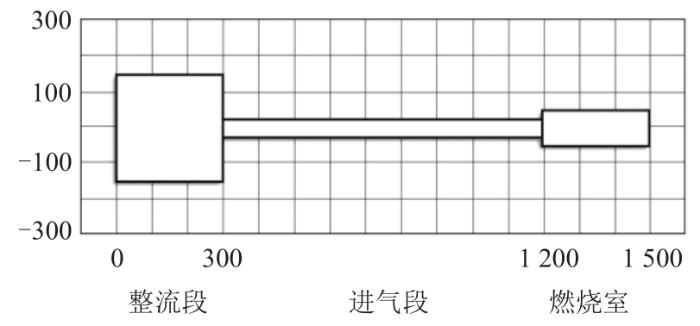
实验系统进气管、旋流器和燃烧室组成如图1所示。实验的对象为丙烷扩散火焰，环境为常温常压。空气由风机经过管路，经蜂窝状整流后从两级旋流器进入燃烧室；燃料从旋流器中心管路经由射流孔进入燃烧室与空气掺混燃烧。燃料中心管路直径d_fuel为12 mm；空气管路外环壁面内直径d_air为50 mm；燃烧室截面为正方形，边长l为100 mm，长度a为300 mm。气流经过燃烧室后直接流入环境中，出口压力为环境压力。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 燃烧室系统测量布局示意图

Fig. 1 Layout diagram of combustion chamber system measurement

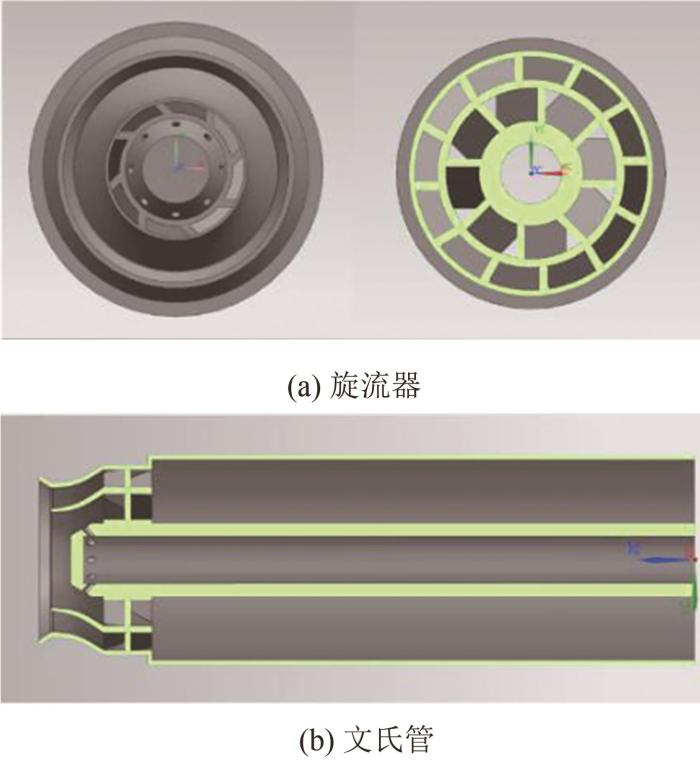
燃烧室头部由燃料喷嘴、旋流器及文氏管构成，旋流器为双级轴向旋流器。一级旋流器与二级旋流器的旋流数分别为0.82和1.08。中心燃料喷嘴出口处有12个燃料射流孔沿周向均匀分布，射流孔直径为1.0 mm。旋流器和文氏管的结构示意图如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 燃烧室旋流器和文氏管的结构示意图

Fig. 2 Structures of combustor swirler and venturi

进气压力脉动与燃烧室压力脉动由动态压力传感器测量，本文采用KD2004动态压力传感器进行压力时序信号测量。释热率脉动由435.3 nm(CH*辐射波长)滤光片与测光探测器组合测量，本文基于CH*离子的浓度与燃烧区单位体积内的释热率存在正比例关系的原理，间接测量释热率脉动。燃烧区发出的光辐射由镀膜滤光片进行滤波(波长为(435.3±10) nm)，使得只有CH*离子产生的光辐射能透过。光强信号采用电压输出型测光探测器CH253进行测量。CH253型测光探测器配备侧窗型光电倍增管，并且配合放大电路，将光强信号转换为电压输出。信号采集系统采用NI的CompactDAQ cDAQ-9178，该设备支持8组采集模块并行采集，满足压力信号和CH*离子光电信号的采集需求。信号采集系统经集成后连接到计算机，实验采样率为2 000 Hz。

本文对不同燃烧工况进行实验研究，当量比变化范围在0.35~0.79，雷诺数保持为10 520。实验工况如表1所示。

表1 实验工况

Tab. 1 Experimental conditions

工况	当量比
S1	0.79
S2	0.71
S3	0.59
S4	0.55
S5	0.47
S6	0.39
S7	0.35

新窗口打开| 下载CSV

2 自激振荡频率特征

在实验中观察到，S1—S4工况下，燃烧较为稳定，监测到的压力信号无明显主频。从工况S5开始，系统开始出现有规律振荡的噪声，随着当量比降低，燃烧噪声和振荡越来越剧烈，在工况S7时振荡强度达到最高。

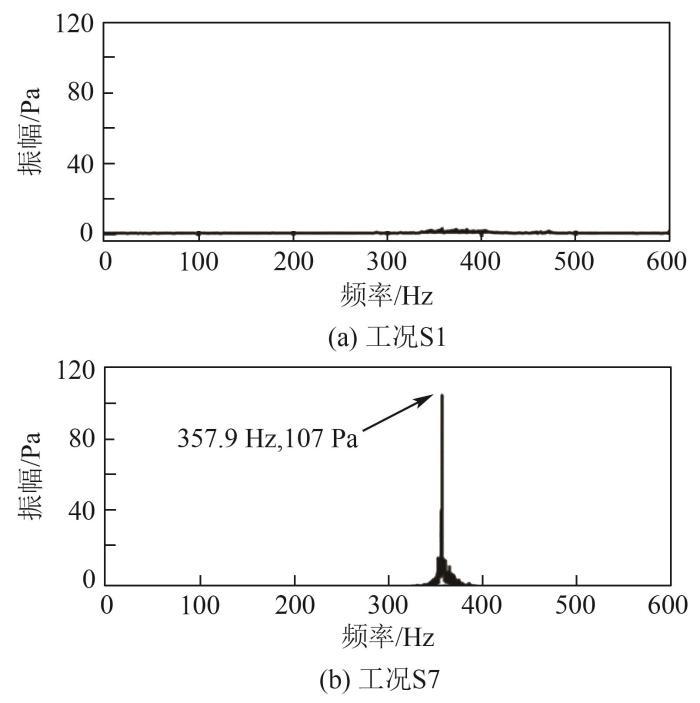
图3为工况S1和S7的压力脉动频域特征，其中：S1稳态工况的频谱图没有典型的峰值；而贫油燃烧工况S7的频谱图在357.9 Hz处出现了明显的峰值，该频率即为S7工况下的振荡频率。根据开口管道经验公式f=c/(2l)可以近似估算系统的一阶固有频率，其中，实验工况测量平均温度为293 K，声速c=343.11 m/s，系统纵向长度l=1.5 m。据此可得到系统的一阶固有频率约为114 Hz，与实验测量得到的频率有所差异，这个差异反映了燃烧的影响。燃烧的影响可通过FDF进行建模，其反映了火焰对速度脉动的响应特性，通常采用热声网络模型进行预测。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 工况S1和S7的傅里叶谱

Fig. 3 Fourier spectrum under operating conditions of S1 and S7

3 热声网络模型

3.1 FDF定义

FDF的概念可以通过线性FTF扩展到非线性区域，形式如下：

F (ω, | u^{'} |) = \frac{Q^{'} / \bar{Q}}{u^{'} / \bar{u}} = G (ω, | u^{'} |) e^{i φ (ω, | u' |)}

(1)

式中： $Q^{'} / \bar{Q}$ 是释热率扰动； $u^{'} / \bar{u}$ 是燃烧室进口速度扰动。

$F (ω, | u^{'} |)$ 通常在频域中表示为增益 $G (ω, | u^{'} |)$ 和相位 $ϕ (ω, | u^{'} |)$ 的形式，它们是激励频率 $ω$ 和振幅 $| u^{'} |$ 的函数。该方法假设扰动具有弱非线性，即谐波激励的火焰响应与激励源有相同频率，但其增益和相位取决于激励振幅和激励频率。

3.2 LOTAN模型

LOTAN模型将系统声学模型与火焰动力学模型结合在一起，已广泛应用于燃烧不稳定性研究。该模型的基本思想是：在声学上，燃烧系统可以表示为由不同模块组成的网络，不同模块对应于系统的各个组件，且具有简单的几何结构。利用线性化的方法对声波行为进行分析建模，并与火焰模型(线性FTF或非线性FDF)相结合，可以确定热声模式的频率、增长率、稳定边界和潜在的极限环振幅等。本研究将其与CFD计算获得的火焰模型相结合，预测不稳定条件下的极限环振荡条件。

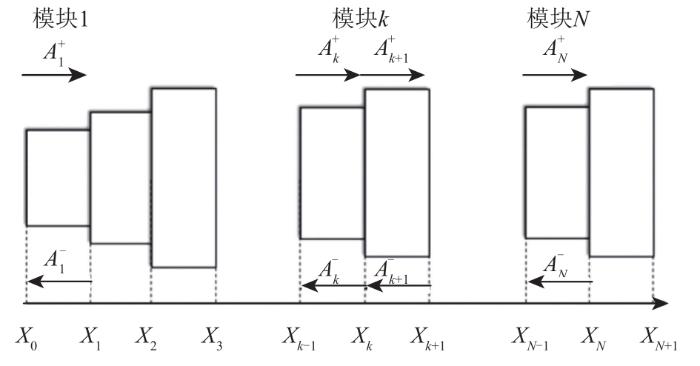
由于元件的横向尺寸与声波波长的比值非常小，故本文的研究只涉及一维平面(纵向)声波，并假设火焰面无限薄。燃烧室的热声网络模型由若干具有不同截面积的模块连接而成，如图4所示。对于模块k，入口和出口分别位于X=X_k_-1和X=X_k，其中k=1, 2, … , N，N是模块的总数。采用位于X=X_n (0≤n≤N)处的无限薄火焰面作为热源，将未燃烧气体和燃烧气体分离。根据线性声学理论，流体的压力、速度、密度可以分解为一个平均值和一个声学扰动(与平均值相比，扰动量较小)^[25]。声场则由正向和反向的平面波叠加而成，考虑到声波在2个方向上传播，故模块k中的压力、速度和密度分别可以表示为：

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 变截面纵向声学元件示意图

Fig. 4 Schematic diagram of variable section longitudinal acoustic elements

p_{k} (x, t) = {\bar{p}}_{k} + p_{k}^{'} (x, t) = {\bar{p}}_{k} + A_{k}^{+} (t - τ_{k}^{+}) + A_{k}^{-} (t - τ_{k}^{-})

(2)

\begin{array}{l} u_{k} (x, t) = {\bar{u}}_{k} + u_{k}^{'} (x, t) = {\bar{u}}_{k} + \frac{1}{{\bar{ρ}}_{k} {\bar{c}}_{k}} [A_{k}^{+} (t - τ_{k}^{+}) - \\ A_{k} (t - τ_{k}^{-})] \end{array}

(3)

\begin{array}{l} ρ_{k} (x, t) = {\bar{ρ}}_{k} + ρ_{k}^{'} (x, t) = {\bar{ρ}}_{k} + \frac{1}{{\bar{c}}_{k}^{2}} [A_{k}^{+} (t - τ_{k}^{+}) + \\ A_{k}^{-} (t - τ_{k}^{-})] - \frac{1}{{\bar{c}}_{k}^{2}} E_{k} (t - τ_{k}^{s}) \end{array}

(4)

式中： $A_{k}^{+}$ 和 $A_{k}^{-}$ 分别为下游和上游传播声波的振幅； $E_{k} = {\bar{ρ}}_{k} {\bar{c}}_{k}^{2} / (C_{p, k} S_{k}^{'})$ 为熵波的振幅； $τ_{k}^{+} = (x - x_{k - 1}) / ({\bar{c}}_{k} + {\bar{u}}_{k})$ ， $τ_{k}^{-} = (x_{k} - x) / ({\bar{c}}_{k} - {\bar{u}}_{k})$ ， $τ_{k}^{s} = (x - x_{k - 1}) / {\bar{u}}_{k}$ 为时间延迟。

将式(2)—(4)代入标准无功流量平衡方程，如果假设马赫数低且线性扰动小，则可以忽略高阶项，并利用稳定项和一阶项平衡方程式来关联上下游声波。将该过程应用到系统中的所有单元，可以得到一个用于描述系统内声波的线性系统。然后导出全局矩阵 $ψ_{1 \to N} (s)$ ，将第1个模块(k=1)和最后一个模块(k=N)中的波连接起来，表示为以下形式：

[\begin{matrix} {\bar{A}}_{N}^{+} (s) \\ {\bar{A}}_{N}^{-} (s) \\ {\tilde{E}}_{N} (s) \end{matrix}] = ψ_{1 \to N} (s) [\begin{matrix} {\bar{A}}_{1}^{+} (s) \\ {\bar{A}}_{1}^{-} (s) \\ {\tilde{E}}_{1} (s) \end{matrix}]

(5)

式中：“~”表示拉普拉斯变换； $s = σ + i 2 π f$ 表示拉普拉斯变量， $σ$ 为增长率，f为频率。

4 数值仿真及结果分析

4.1 LES计算

为了得到适合的火焰模型，进而预测系统的自激振荡频率，本文采用LES方法建立了火焰的不稳定热释放对不同入口速度扰动的响应特征。LES亚网格模型采用壁面自适应局部涡黏(wall-adapting local eddy-viscosity，WALE)模型，壁面采用无滑移壁面边界条件；出口边界采用压力出口边界条件。燃烧模型采用涡耗散模型(eddy-dissipation model，EDM)，化学反应机理为丙烷和空气的总包化学反应。在实验中，外部激励是通过安装在燃烧室上游的2个扬声器引入的，为了模拟这种激励，进口空气速度通过UDF给出，表示为平均速度叠加一个单频谐波的形式：

u = \bar{u} [1 + \frac{u'}{\bar{u}} s i n (2 π f t)]

(6)

在模拟中， $u' / \bar{u}$ 和f独立变化，以此获得FDF。

选取振荡工况S7作为计算工况，在不同的激励频率和振幅下进行LES计算，共计24种激励工况，扰动频率分别为100、200、300、350、400、600 Hz，对于每个扰动频率，执行4个激励振幅，即 $u' / \bar{u}$ =0.1, 0.2, 0.3, 0.4。速度脉动监测点设置在位于临近燃烧室入口的旋流器出口，释热率为对燃烧室释热率的体积积分。对于不同的入口速度扰动，通过FFT分析释热率对速度扰动的响应特征。

4.2 FDF拟合

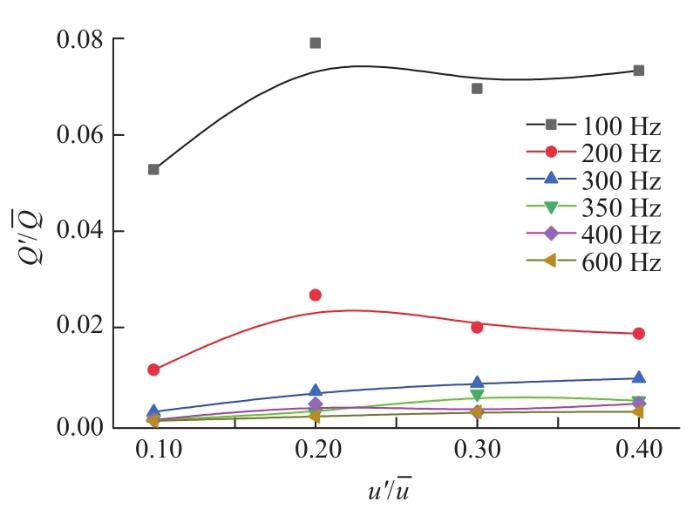
图5为释热率扰动随速度扰动的变化情况。可以看出，所有激励频率下的释热率扰动在速度扰动增大到某一值后，均开始出现饱和特征，即当速度扰动幅值达到临界值后，扰动幅值若继续增加，释热率扰动幅值将趋于饱和，不再继续增加，而是保持不变^[26]。低频激励(_{f=100, 200 Hz)下，释热率响应幅值较大，当频率大于300 Hz时，释热率响应的幅值随速度振幅变化不大，这说明释热率响应对低频激励较为敏感。在频率为350 Hz(接近自激振荡频率f_{=357.9 Hz)时，释热率响应的幅值在4个激励振幅上几乎是恒定的。这种现象可能是由于振荡在这个位置建立了极限环，因此在激励作用下能够保持稳定。}}

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 不同频率下LES计算得到的释热率扰动随速度扰动的变化情况

Fig. 5 Variation of heat release rate disturbance with velocity disturbance calculated by LES under different frequencies

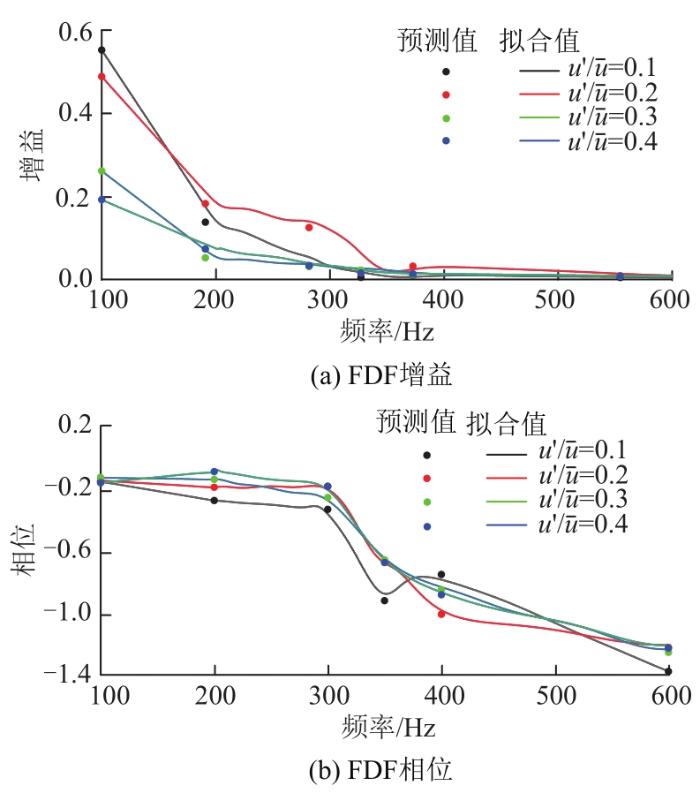
利用FFT对释热率和速度脉动的时序信号进行处理，得到频域内FDF的增益和相位。图6为当前LES预测的FDF结果以及16阶拟合获得的响应特征。从整体上来看，增益 $G (ω, | u^{'} |)$ 都随着激励频率的增大而减小；随着激励振幅的增大，增益通常减小，由于线性响应不会随激励而发生振幅的变化，所以增益的非线性很明显。对于100 Hz的低频激励，相位 $ϕ (ω, | u^{'} |)$ 随速度振幅的变化很小。当激励频率大于100 Hz时，相位随速度振幅的变化较为明显，在350 Hz附近达到最大，这种大的相位变化可能导致振荡达到极限环状态。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 预测的FDF结果以及通过16阶拟合后的结果

Fig. 6 Predicted FDF results and fitting lines obtained by the 16th order fitting

4.3 低阶模型燃烧不稳定性预测

由于LOTAN模型法将流动简化为一维，且各向同性，故建模时需将各模块简化为旋转体。简化后的实验系统截面为圆形，面积发生变化，故进气速度需通过流量守恒方程进行折算。系统模型如图7所示，包括整流段、进气段和一个带有开放端的燃烧室。模型长度和实验装置保持一致，截面半径分别为150、25、50 mm。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 系统模型示意图

Fig. 7 Schematic diagram of system model

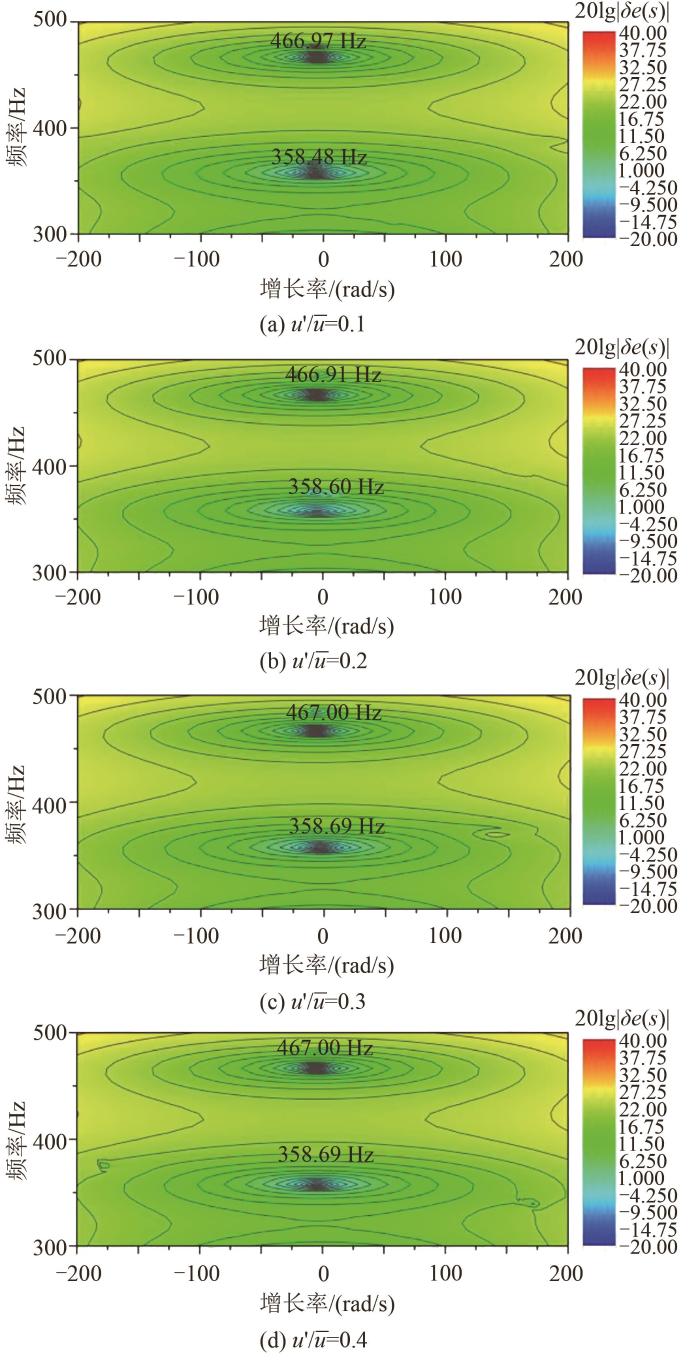
将上述拟合的FDF数据结果导入热声网络模型，对获得的每组数据进行16阶拟合，然后计算对应的热声模式，可以获得特征值随速度扰动的变化规律。绘制 $20 l g |δ e (s)|$ 的等高线图，其中 $δ e (s)$ 为出口边界处的误差，该值反映了计算结果对出口声学边界的满足程度。图8为特征值的位置(增长率和频率)及其所在等高线，由于特征值满足出口边界条件，因此误差最小。负增长率表示振荡衰减，系统会趋于稳定；正增长率表示振荡为正反馈模式，系统会趋于不稳定。主要模式在图中用三角形表示。结果表明：对于4个速度扰动 $u' / \bar{u}$ =0.1, 0.2, 0.3, 0.4，系统在实验频率附近有2个主要模式，分别为359 Hz和467 Hz。对于467 Hz模式，所有速度振幅下的增长率均为负，说明系统趋于稳定，不太可能在此主频建立振荡模态，且与359 Hz附近的模式相比，距零增长率的位置更远，说明359 Hz附近的模式更容易发生自激振荡。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 不同振幅速度扰动下特征值位置(增长率和频率)的等值线图

Fig. 8 Contour map of eigenvalue location (growth rate and frequency) under different amplitude velocity disturbances

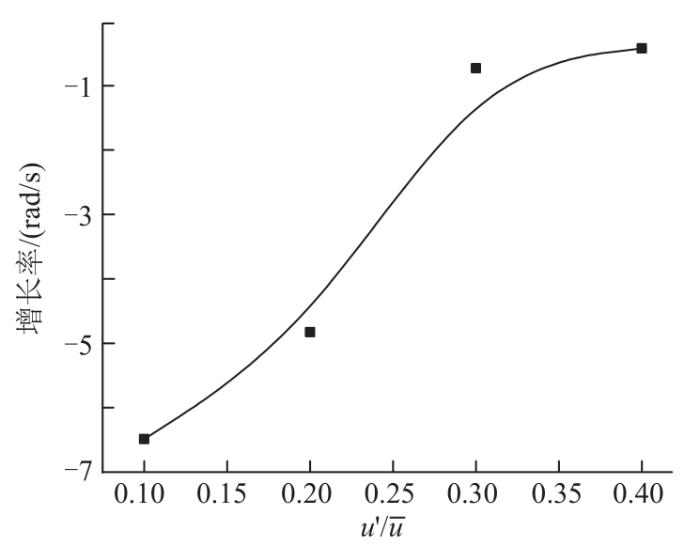
在359 Hz附近，系统增长率随速度扰动的变化如图9所示，可以看出，4个速度扰动下系统增长率分别为-6.49、-4.83、-0.73、-0.42 rad/s。随着速度扰动增加，系统增长率趋近于0，这意味着在359 Hz附近系统会建立稳定振荡模态。该值与实验值相比，误差约为0.3%，吻合较好。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 在359 Hz附近系统增长率随速度扰动的变化

Fig. 9 Variation of system growth rate with velocity disturbance near 359 Hz

由于不同进气振荡强度所获得的特征频率十分接近，所以无法根据预测的特征频率进行反演，以获得可能的进气扰动程度。同时，实验中的振荡主频在当量比0.35~0.47内维持在358 Hz附近不变，且预测的频率值与实际值相差不大，因此证实了该预测方法较为合理。

5 结论

1）在模型燃烧室贫燃条件下运行会发生振荡燃烧，随着当量比降低，燃烧噪声和振荡越来越剧烈，频谱图上出现峰值明显的主频。

2）通过LES数值仿真发现，所有激励频率下的释热率扰动在速度扰动增大到某一值后均会达到饱和，且低频激励下释热率扰动对速度扰动较为敏感。拟合出的FDF在接近自激振荡频率附近时，相位随速度振幅的变化达到最大，这种大的相位变化可能导致振荡达到极限环状态。

3）通过FDF结合LOTAN分析发现，在300~500 Hz范围内，热声系统存在2种模式，分别位于359 Hz和467 Hz附近，且随着扰动幅值的增长，359 Hz附近的模态逐渐从稳定模态过渡到振荡模态，与实验值相比，预测误差约0.3%。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

黄亮

．

LPP低污染燃烧室振荡燃烧机理研究

[D]．南京：南京航空航天大学，2017．