1 000 MW煤电机组调峰中汽温控制策略研究

doi:10.12096/j.2096-4528.pgt.21024

1 000 MW煤电机组调峰中汽温控制策略研究

闫修峰¹, 宗珂¹, 何修年¹, 高林², 秦斌², 王明坤², 惠文涛²

1.华电邹县发电有限公司, 山东省邹城市 273522

2.西安热工研究院有限公司, 陕西省西安市 710054

Research on Steam Temperature Control Strategy in Peak Regulation of 1 000 MW Coal Power Unit

YAN Xiufeng¹, ZONG Ke¹, HE Xiunian¹, GAO Lin², QIN Bin², WANG Mingkun², HUI Wentao²

1.Huadian Zouxian Power Corporation Ltd. , Zoucheng 273522, Shandong Province, China

2.Xi’'an Thermal Power Research Institute Co. , Ltd. , Xi’an 710054, Shaanxi Province, China

收稿日期: 2021-11-15

基金资助:

国家重点研发计划项目. 2019YFB1505400

Received: 2021-11-15

作者简介 About authors

闫修峰(1969)，男，高级工程师，主要研究方向火力发电企业安全生产管理，13355116815@163.com；

秦斌(1981)，男，工程师，主要研究方向智能化电站应用，qinbin@tpri.com.cn。

摘要

在燃煤机组快速调峰、调频的响应过程中，将汽温快速地控制在合理的范围区间是自动控制领域面临的难点之一。由于汽温具有大惯性、大延迟特性，采用常规的串级控制器往往达不到较好的控制效果。同时依赖模型精度的预测控制与神经网络等高级算法，受汽温控制对象非线性、测量不确定性以及时变特性的影响，限制了其在实际控制中的应用。为此，提出了一种基于串级与局部Smith预估的混合控制模型，通过参数辨识获得局部Smith预估的精确模型，构建了混合结构的汽温控制策略，并于某1 000 MW超超临界锅炉减温水系统中进行应用，结果表明：该方法高效、易用、稳定，可有效地改善汽温控制性能，达到良好的控制效果。

关键词： 1 000 MW超超临界锅炉 ; 燃煤机组 ; 汽温控制 ; 局部Smith预估 ; 调峰 ; 调频

Abstract

In the response process of rapid peak regulation and frequency regulation of coal-fired units, quickly controlling the steam temperature within a reasonable range is one of the difficulties in the field of automatic control. Due to the large inertia and large delay characteristics of steam temperature, the conventional cascade control often fails to achieve better control results. Meanwhile, advanced algorithms such as model prediction and neural networks are affected by non-linearity, measurement uncertainty and time-varying characteristics of temperature object, which limits their application in actual control. This paper proposed a hybrid control model based on cascade and local Smith prediction. The accurate local Smith prediction model was obtained through parameter identification method, and the steam temperature control strategy based on the hybrid structure was constructed and applied in the 1 000 MW ultra-supercritical boiler desupercritical water system. The results show that the method is efficient, easy to use and stable, which can effectively improve the performance of steam temperature control and achieve good control effects.

Keywords： 1 000 MW ultra-supercritical boiler ; coal-fired units ; steam temperature control ; local Smith prediction ; peak regulation ; frequency regulation

PDF (1348KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

闫修峰, 宗珂, 何修年, 高林, 秦斌, 王明坤, 惠文涛. 1 000 MW煤电机组调峰中汽温控制策略研究. 发电技术[J], 2022, 43(3): 518-522 DOI:10.12096/j.2096-4528.pgt.21024

YAN Xiufeng, ZONG Ke, HE Xiunian, GAO Lin, QIN Bin, WANG Mingkun, HUI Wentao. Research on Steam Temperature Control Strategy in Peak Regulation of 1 000 MW Coal Power Unit. Power Generation Technology[J], 2022, 43(3): 518-522 DOI:10.12096/j.2096-4528.pgt.21024

0 引言

对于燃煤机组，主汽温和再热汽温是评价锅炉运行安全性和经济性的重要指标之一。为了实现火电行业节能减排的目标，燃煤机组逐渐向着高参数、大容量的方向发展，提升主汽温和再热汽温可以有效提高机组的循环效率。然而，随着我国能源结构的转型，新能源的大规模并网使常规燃煤机组需承担越来越多的调峰、调频任务，超温爆管等现象普遍成为制约超(超)临界机组提升变负荷速率的核心瓶颈。

减温水系统通常是针对汽温异常或事故情况设计的，但在机组快速调峰、调频的响应过程中，减温水控制逐渐被迫成为动态过程锅炉壁温和蒸汽温度控制的常用手段。

由于锅炉汽温具有非线性、大惯性和滞后性等特性，使得减温水控制面临巨大挑战，以过热汽温为例，采用常规的串级控制器往往达不到较好的控制效果。目前，国内外学者针对汽温大惯性和大延迟系统控制开展了大量研究，并提出许多先进的控制策略。现代先进控制算法中，模型预测控制(model prediction control，MPC)^[1-2]和Smith预估控制^[3-4]等常被用于改进汽温控制。模型预测、神经网络等高级算法对模型误差比较敏感，尽管对减温水控制及其目标系统进行建模的研究较多^[5-10]，但由于实际系统具有较强的非线性、测量不确定性和时变特性，使实际应用过程难以解决模型失配问题。此外，逆神经控制器^[7]和回归支持向量机^[8]也用于减温水控制的研究，然而这些方法大多用于仿真环境，难以长期保持实际效果，限制了其在实际控制中的应用。本文在前述研究基础上，从喷水减温对象系统工艺特点出发，提出局部Smith预估校正汽温控制策略，规避了算法的模型失配风险同时，有效改善了控制性能。

1 减温水系统非线性特性分析

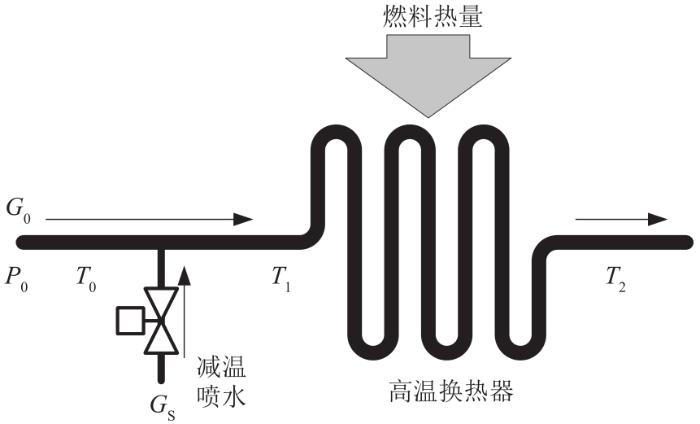
过热汽温一般采用串级控制，再热汽温一般采用单回路控制，均设有减温喷水装置。换热器的减温水结构示意图如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 减温水结构示意图

Fig. 1 Schematic diagram of desuperheating water structure

换热器出口汽温目标设定值为 ${\hat{T}}_{2}$ ，减温器出口混合汽温 $T_{1}$ 作为辅助变量，共同构成经典串级比例-积分-微分(proportion-integral-differential，PID)控制模型，如图2所示。其中：PID₁和PID₂分别为串级控制的主调节器和副调节器； $G_{1} (s)$ 为减温水与高温蒸气混合过程的传递函数； $G_{2} (s)$ 为换热器传热过程的传递函数； $D_{1} (s)$ 为过热蒸汽的外部扰动； $D_{2} (s)$ 为烟气侧的外部扰动。该控制方法被广泛地应用于汽温控制。

图2

新窗口打开| 下载原图ZIP| 生成PPT

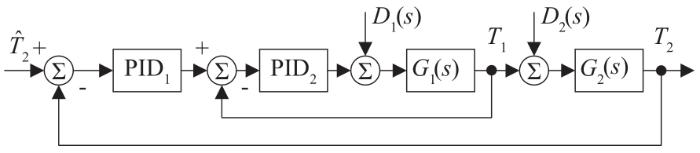
图2 汽温控制系统串级PID控制模型

Fig. 2 Cascade PID control model of steam temperature control system

流动与换热过程使减温喷水控制成为典型的大惯性与大延迟系统，各种先进控制方法被用来尝试代替传统的PID控制。

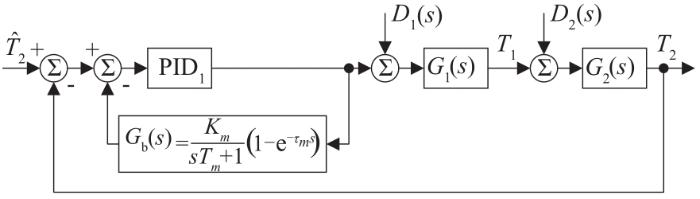
Smith预测控制在大时滞对象的控制中非常流行^[11-13]，并能体现出较优的控制效果。Simith预估校正控制模型如图3所示，为了避免系统大惯性大延迟对控制造成的不必要振荡，通过带有延迟的 $G_{b} (s)$ 将控制器输出反馈至输入，以补偿实际系统输出反馈的惯性与延迟作用，从而提高系统的控制稳定性。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 Simith预估校正控制模型

Fig. 3 Smith predictive control model

该校正作用的核心在于利用系统近似的响应模型 $G_{b} (s)$ 尽可能抵消控制大惯性、大延迟的影响，因此 $G_{b} (s)$ 与 $G_{1} (s)$ 、 $G_{2} (s)$ 的相似性极为关键。

实践经验表明，减温水阀流量非线性和喷水流量测量不确定性是制约模型预测控制等技术应用的关键问题。一方面，减温水阀的实际运行特性随机组运行工况的变化而变化；另一方面，对于大多数机组，小开度、频繁开关是阀门的常态，这会加速阀门发生气蚀等缺陷，从而改变阀门特性。同时，减温水流量的测量往往偏离孔板流量计的测量线性区域。因此，减温水流量作为一个关键参数，并不能满足精确控制的要求，在建模精确度和模型应用上都存在较大偏差。

综上所述，受减温水阀门的非线性、测量不确定性和时变特性的影响，其流量特性很难建立精确的模型用于模型预测控制方法，这就是Smith预估等依赖模型精度的控制方法和人工神经网络控制难以直接用于减温喷水控制的主要原因之一。

2 基于局部Simith预估的混合控制模型

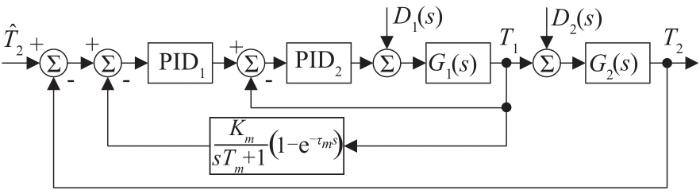
本文提出了一种基于串级和局部Smith预估校正的混合控制模型，如图4所示。为了保证模型预测控制的实际应用、提高模型精度，将减温水与高温蒸气混合过程 $G_{1} (s)$ 的模型分离出来，构建减温水与高温蒸气混合后流经过热器/再热器进行换热的局部Smith预估模型。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 混合控制模型

Fig. 4 Hybrid control model

在具有可靠性的串级控制的基础上，通过混合后温度 $T_{1}$ 进行Smith预测校正出口温度偏差，以解决传热部分 $G_{2} (s)$ 的大惯性和大延迟问题，从而提高原有的串级控制性能。

减温水与高温蒸气混合后流经过热器/再热器进行换热，这一换热过程主要由惯性环节和延迟环节组成。忽略锅炉稳态工况下传热能力的变化，混合后蒸汽温度 $T_{1}$ 与出口温度 $T_{2}$ 之间的模型可化简为经典的一阶惯性模型和纯延迟模型，将模型误差考虑为3个等效模型参数，即增益、惯性时间和延迟时间。

构建局部Smith预估动态模型为

G (s) = \frac{K_{m}}{s T_{m} + 1} (1 - e^{- τ_{m} s})

⑴

式中： $K_{m}$ 为动态模型增益； $T_{m}$ 为动态模型惯性时间常数； $τ_{m}$ 为动态模型延迟时间常数。

此外，局部Smith预估回路可以与串级PID控制器或者一些其他控制器分开使用。

3 参数辨识与模型验证

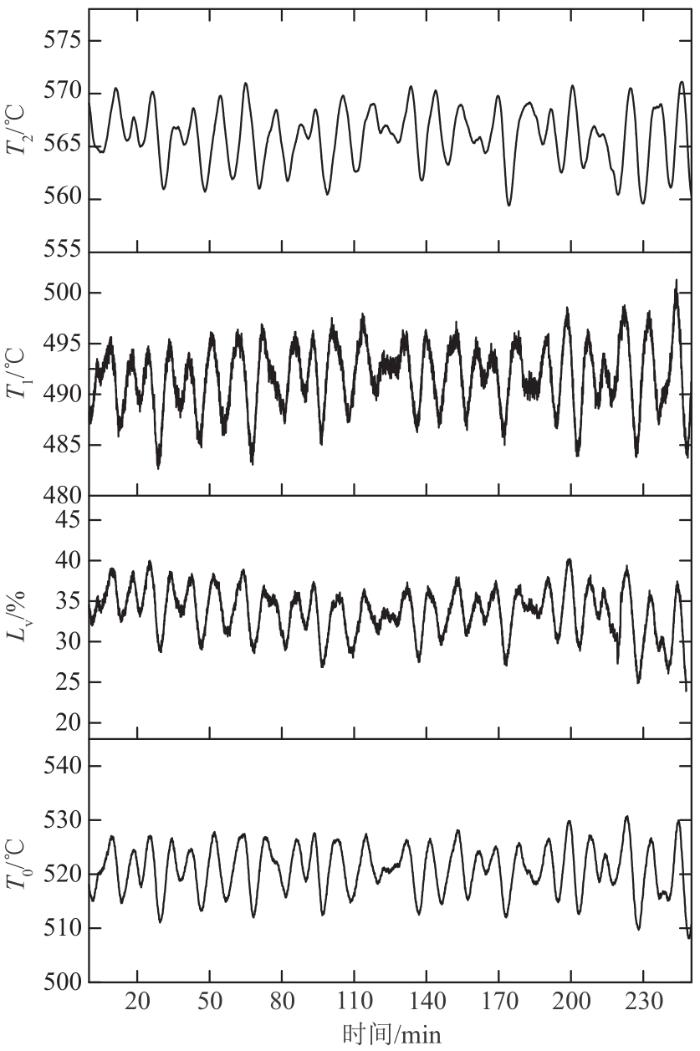
针对某超临界燃煤直流锅炉高温过热器进行了试验研究，在锅炉状态基本稳定情况下，记录4 h左右的数据，如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 某超临界燃煤直流锅炉过热器的试验数据

Fig. 5 Test data of a superheater in a supercritical coal-fired once-through boiler

采用最小二乘参数辨识方法^[14-15]，以 $T_{1}$ 为输入， $T_{2}$ 为输出，辨识局部Smith预估模型参数，辨识的参数如表1所示。

表1 辨识的模型参数

Tab. 1 Identified model parameters

参数	增益 $K_{m}$	惯性时间 $T_{m}$ /s	延迟时间 $τ_{m}$ /s
数值	1.12	190.99	54.77

新窗口打开| 下载CSV

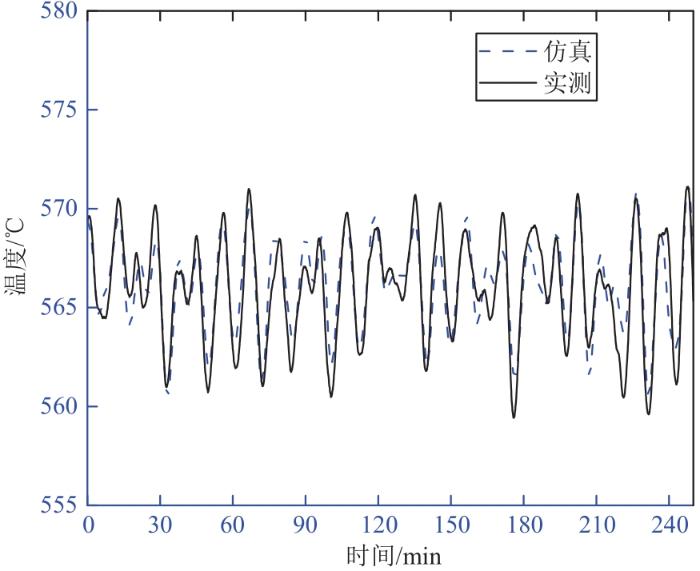
将辨识后的局部Smith预估模型的仿真结果与记录数据进行对比，如图6所示。通过对仿真曲线与4 h左右的实测数据进行比较，可以看出二者达到了良好的一致性，即使在某段时间内存在一定的偏差，曲线的波动趋势仍能与试验数据很好地吻合，有助于控制器准确地预估换热器出口温度。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 仿真结果和测量数据的比较

Fig. 6 Comparison of estimated simulation results and test data

4 混合控制模型应用

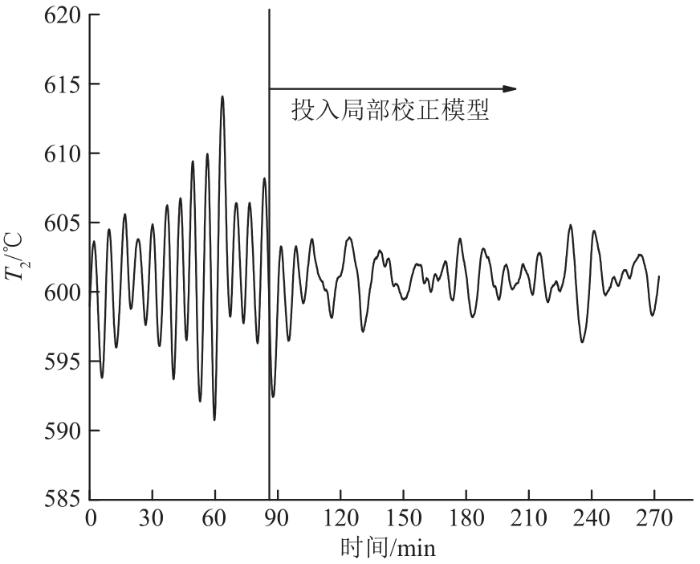
本文设计的混合控制模型在1 000 MW超超临界锅炉减温水控制中进行实际应用，与经典的串级控制相比，结合局部Smith预估校正可以为减温水控制获得更好的效果。图7显示了其在1 000 MW超超临界锅炉上的应用效果，与原串级PID控制相比，本文提出的基于串级与局部Smith预估校正的混合模型控制可以随着机组运行工况的变化有效地改善汽温控制性能，最大控制偏差快速回落至±5 ℃之内。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 混合控制模型在1 000 MW直流锅炉中的应用

Fig. 7 Application of the proposed hybrid control model in an ultra-suppercritical 1 000 MW once-through boiler

通过增益因子 $K_{m}$ 可以调整预测校正的强度。与其他改进的控制器相比，本文提出的方法更简单，更易于现场调试。

5 结论

在普遍提升燃煤机组快速调峰、调频响应灵活性需求的大背景下，将汽温快速地控制在合理的范围区间是关键的核心瓶颈之一。为此，提出了一种基于串级与局部Smith预估的混合控制模型，并于1 000 MW超超临界锅炉减温水系统中进行应用，结果表明：

1）该方法高效、易用、稳定，可有效地改善汽温控制性能，达到良好的控制效果。

2）该模型能有效地解决模型预测控制方法无法应用于实际控制的难题，同时通过局部Smith预估可以获得较为精确的预估模型，从而指导超前减温水的控制，有效地提高经典串级PID的控制效果，获得更好的汽温控制指标。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

袁立川，丁艳军，李东海．

过热汽温多模型预测控制的现场应用

[J]．清华大学学报(自然科学版)，2010，50(8)：1258-1262．