图1
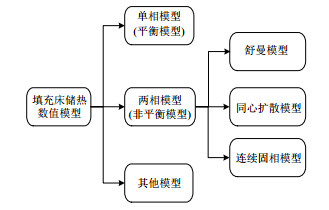
填充床储热数值模型分类
Fig. 1
Classification of stored heat storage numerical models
图2
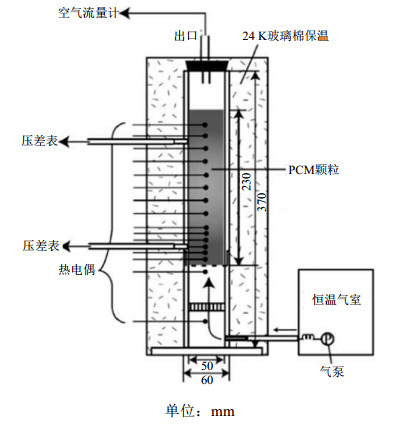
PCM颗粒与空气直接换热实验系统
Fig. 2
PCM particle and air direct heat exchange experimental system
1.3.1 舒曼模型 舒曼模型[18 ] 主要用于分析填充床的传热特性。该模型假设为一维传热,忽略了HTF和PCM的径向和轴向导热。分别建立HTF和PCM的能量方程,如式(2)和(3)所示。
(2) $\begin{array}{l}\varepsilon {C_{{\rm{p}}, {\rm{f}}}}{\rho _{\rm{f}}}(\frac{{\partial {T_{\rm{f}}}}}{{\partial t}} + u\frac{{\partial {T_{\rm{f}}}}}{{\partial x}}) = {h_{{\rm{PCM}} - {\rm{HTF}}}}({T_{{\rm{PCM}}}} - {T_{\rm{f}}}) - \\{\rm{ }}{U_{\rm{L}}}({T_{\rm{f}}} - {T_{{\rm{ENV}}}})\end{array}$
(3) $(1 - \varepsilon ){\rho _{{\rm{PCM}}}}\frac{{\partial H}}{{\partial t}} = {h_{{\rm{PCM - HTF}}}}({T_{\rm{f}}} - {T_{{\rm{PCM}}}})$
式中:T f 为流体温度;T ENV 为环境温度;T PCM 为相变材料温度;h PCM-HTF 为对流换热系数;U 为热透射率。
式(2)右侧2项分别为HTF与PCM的对流换热项和热损失项,在保温良好的条件下热损失项一般可以忽略。该模型对PCM采用集总参数法,并假设对流换热系数与时间和空间无关,可以有效提高计算效率。然而,舒曼模型中没有考虑PCM内部的热传导作用,因此其局限性在于它无法描述PCM内部的传热过程,只考虑对流驱动的传热过程。如前文所述,大多数PCM具有低导热的特性,使得PCM导热热阻在蓄放热的传热过程中起重要作用。因此,部分研究者通过在对流传热项中加入修正项来分析PCM自然对流热阻对传热过程的影响。
Felix等[19 -20 ] 利用舒曼模型研究了太阳能热水系统的PBLTES系统热性能。其数值模型在能量方程中定义了总传热系数U 0 ,其中包含对流传热热阻、封装球壳导热热阻以及PCM相变传热热阻。该系数定义为
(4) ${U_0} = \frac{1}{A}\frac{1}{{{R_{{\rm{ext}}}} + {R_{\rm{c}}} + {R_{{\rm{in}}}}{\rm{(}}t{\rm{)}}}}$
式中:R ext 是对流热阻;R c 是封装球壳的导热热阻;R in (t )是封装球内PCM的相变传热热阻,该热阻随PCM固液界面的变化而变化,受熔融层的导热和自然对流影响很大。即使该模型没有考虑封装球内的温度梯度,也会通过总传热系数随时间的变化来反映封装球内部的传热过程。
Tumilowicz等[21 ] 用类似的舒曼修正模型研究了填充床斜温层。利用等效对流传热的方法,并采用特征值的方法来求解方程。结果证明,特征值方法可以高效计算预测填充床斜温层的运行状态。
杨晓西等人[22 -24 ] 模拟分析了熔融盐高温填充床蓄热罐显热蓄热系统传热特性,并分析了各运行参数对系统的影响;结合相变蓄热特性,开发基于舒曼模型的填充床相变蓄热系统模型,研究了相变蓄热系统传热与流动特性及各影响因素对其蓄热性能的影响。
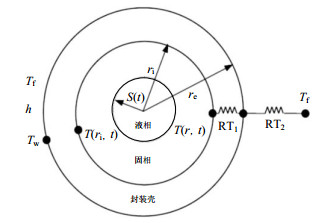
1.3.2 同心扩散模型 该模型由Ismail和Henríquez[25 ] 开发,模型中将填充床储热罐沿轴向分成许多微元层,HTF沿轴向递进流动传热。假设流体的温度是均匀的,并且等于所在层的平均温度。当HTF与PCM封装球存在温差时,考虑了球壳外表面对流传热热阻和球壳厚度的导热热阻,模型中假定球内传热过程为纯热传导。使用有限差分法和移动网格技术进行求解,并使用实验数据验证了模型的有效性。研究了HTF入口温度、质量流量和封装球导热率对蓄放热时间的影响。
该模型将填充床视为由独立球体组成的各向同性多孔介质,这种方法可以计算球内的温度分布。该模型的特点在于:开始阶段HTF与PCM发生显热交换,球体外表面与传热流体进行对流换热,热量通过球壳以导热的形式由外表面传递至内表面,直至球壳内表面达到相变温度,与球内表面接触的PCM形成第一层相变层,随着传热的传入,球内相变层随时间逐渐演变,如图3 所示。
10.12096/j.2096-4528.pgt.19062.F003 图3 球形PCM能量平衡示意图 Spherical PCM energy balance diagram Fig. 3 能量守恒方程中包括HTF和PCM中的轴向导热,如式(5)—(7)所示。
(5) $\begin{array}{l}\varepsilon {C_{{\rm{p}}, {\rm{f}}}}{\rho _{\rm{f}}}(\frac{{\partial {T_{\rm{f}}}}}{{\partial t}} + u\frac{{\partial {T_{\rm{f}}}}}{{\partial x}}) = \varepsilon {k_{\rm{f}}}\frac{{{\partial ^2}{T_{\rm{f}}}}}{{\partial {x^2}}} + {h_{{\rm{PCM}} - {\rm{HTF}}}} \cdot \\ {\rm{ }}({T_{{\rm{PCM}}}} - {T_{\rm{f}}}) - {U_{\rm{L}}}({T_{\rm{f}}} - {T_{{\rm{ENV}}}})\end{array}$
(6) $\begin{array}{l}(1 - \varepsilon ){\rho _{{\rm{PCM}}}}\frac{{\partial H}}{{\partial t}} = (1 - \varepsilon ){k_{{\rm{PCM}}}}\frac{{{\partial ^2}T}}{{\partial {x^2}}} + \\{\rm{ }}{h_{{\rm{PCM}} - {\rm{HTF}}}}({T_{\rm{f}}} - {T_{{\rm{PCM}}}})\end{array}$
(7) ${\rho _{{\rm{PCM}}}}\frac{{\partial H}}{{\partial t}} = \frac{1}{{{r^2}}} \cdot \frac{\partial }{{\partial r}}({k_{{\rm{PCM}}}}{r^2}\frac{{\partial T}}{{\partial r}})$
式中:k f 为流体导热系数;k PCM 为相变材料导热系数。
式(5)为HTF的能量守恒方程,右侧第1项为轴向导热项,第2项为对流传热项,第3项为热损失项。式(6)和(7)分别为PCM在边界处和球内部的能量守恒方程。同心扩散模型中流体温度均匀,同层球体的传热规律相同。
Wu等[26 ] 使用修正的二维同心扩散模型研究了封装高温相变材料的填充床蓄热系统,动量方程中引入了填充层孔隙区惯性系数和渗透率。模型中使用有效导热系数考虑球内液相PCM的自然对流,没有考虑环境损失,且认为储热介质的物性参数为定值。分析了填充高温熔盐PCM蓄放热过程的动态性能。研究结果对实际约束条件下高温PBLTES系统的最佳运行和设计参数具有借鉴意义。
Bédécarrats等[27 ] 提出了另一种同心扩散模型。该模型既考虑了周围流体的传热,又考虑了封装PCM内部的过冷现象。
Galione等[28 ] 利用同心扩散模型,与HTF动量方程相结合,研究了聚光太阳能电厂中相变储热装置“斜温层”热性能,利用Pacheco等的实验数据对模型进行了验证,并得出结论:如果PCM层位于斜温层顶部和底部,则可充当“缓冲层”,使得出口温度接近熔化温度。此外,他们还证明了使用多级PCM可抑制斜温层的退化,提高系统总储热效率。
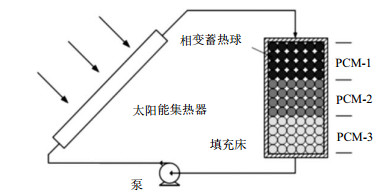
Yang等29] 建立同心扩散模型,对多级相变材料(T m1 =60~62℃,T m2 =50~52℃,T m3 =42~44 ℃)的太阳能填充床储热系统进行数值研究。模拟了具有不同熔点PCM的组合式太阳能填充床储热系统,如图4 所示。该系统以南京某典型夏季的气象条件为环境参数,模拟了太阳能集热器的性能。通过蓄放热效率和㶲分析表明,与单一PCM填充床系统相比,多级PCM填充床系统多级PCM熔化更快,蓄热时间更短,具有更高的热效率和㶲效率。
10.12096/j.2096-4528.pgt.19062.F004 图4 组合式太阳能填充床储热系统 Combined solar packed bed heat storage system Fig. 4 此外,Bindra等[30 ] 基于同心扩散模型和㶲分析模型,研究了填料床在循环储存和回收过程中的动态热响应。该模型中考虑了环境损失、PCM球内的温度梯度以及HTF和PCM的轴向热传导。研究结果表明,在较高的储热温度条件下,为了获得更高的㶲回收率,需要系统具有较低的潜热或较低的能量密度。然而,即使在高能量密度的显热蓄热系统中,也可以获得较高的㶲回收率,该结论对于新能源电站大规模应用储热技术具有重要意义。
Panesi[31 ] 设计了应用于HVAC系统的填充床蓄冷装置。该系统球形封装水与成核剂(相变温度0 ℃)为PCM,乙醇水溶液为HTF,采用有限差分法和移动网格技术进行计算。结果表明,HTF质量流量和入口温度对蓄冷时间的影响最大。
Cheng等[32 ] 设计了用于太阳能制冷系统中的填充床蓄冷装置。该装置采用了复合相变材料,通过不同条件下的热性能分析发现,随着HTF入口温度由7 ℃升高至12 ℃,平均储热速率、最大储热容量和㶲效率分别下降了73.9%、44.7%和10.4%。进一步研究了串联填充床储冷装置,得出了3~5级为推荐的CTES串联级数。
赵炳晨[33 ] 基于同心扩散模型、焓方法及有效导热系数法建立了熔盐单罐填充床蓄热系统的一维瞬态传热数学模型,分析了蓄放热循环过程中系统的性能。量化了不完全蓄热效应对蓄热性能的影响,采用控制变量法研究了关键设计参数对4种填充床蓄热系统蓄热性能的影响。
1.3.3 连续固相模型 连续固相模型将储热球看作具有孔隙结构的连续介质,不单独对球体内部的热梯度进行建模。该模型在能量方程中增加了轴向(一维模型)和径向(二维模型)上的热传导。由于增加了径向方向上的热传导,大幅度增加了模型的计算成本,但是连续固相模型是唯一能够分析径向方向上热梯度对整个储热过程影响的模型,在因低质量流量而导致具有较大热损失的系统或入口流量分布不均匀的系统中显得尤为重要。控制方程如式(8)和(9)所示。
(8) $\begin{array}{l}\varepsilon {C_{{\rm{p}}, {\rm{f}}}}{\rho _{\rm{f}}}(\frac{{\partial {T_{\rm{f}}}}}{{\partial t}} + u\frac{{\partial {T_{\rm{f}}}}}{{\partial x}}) = {k_{{\rm{f, x}}}}\frac{{{\partial ^2}{T_{\rm{f}}}}}{{\partial {x^2}}}{\rm{ + }}{k_{{\rm{f, r}}}}(\frac{{{\partial ^2}{T_{\rm{f}}}}}{{\partial {r^2}}} + \frac{1}{r}\frac{{\partial {T_{\rm{f}}}}}{{\partial r}}) + \\\;\;\;\;\;\;\;{h_{{\rm{PCM}} - {\rm{HTF}}}}({T_{{\rm{PCM}}}} - {T_{\rm{f}}}) - {U_L}({T_{\rm{f}}} - {T_{{\rm{ENV}}}})\end{array}$
(9) $\begin{array}{l}(1 - \varepsilon ){\rho _{{\rm{PCM}}}}\frac{{\partial H}}{{\partial t}} = (1 - \varepsilon ){k_{{\rm{PCM}}, {\rm{x}}}}\frac{{{\partial ^2}T}}{{\partial {x^2}}}{\rm{ + }}\\{k_{{\rm{PCM, r}}}}(\frac{{{\partial ^2}T}}{{\partial {r^2}}} + \frac{1}{r}\frac{{\partial T}}{{\partial r}}) + {h_{{\rm{PCM}} - {\rm{HTF}}}}({T_{\rm{f}}} - {T_{{\rm{PCM}}}})\end{array}$
式中:k f, x 为流体轴向导热系数;k f, r 为流体径向导热系数;k PCM, x 为相变材料轴向导热系数;k PCM, r 为相变材料径向导热系数。
Cheralathan等[34 ] 对基于PCM的蓄冷装置建立了一维连续固相模型并对其进行了实验验证。利用该模型对蓄冷系统性能进行参数分析,研究了空隙率、斯坦顿数、斯蒂芬数和贝克莱数对其性能影响。结果表明,该模型可以有效计算蓄冷系统传热特性。
Benmansour等[35 ] 建立了以空气作为HTF,石蜡作为PCM的二维连续固相模型,并利用有限差分法对控制方程进行求解。通过实验证明了该模型在不同普朗特数下均适用,并可以应用于雷诺数范围较大的蓄放热过程中。
Arkar等[36 ] 使用二维连续固相模型研究基于2个填充床潜热储热装置的机械通风系统的性能,并通过实验进行验证。建立了基于储热量、空气流量和PCM物性的温度响应经验方程,并用于TRNSYS模拟中。
Nallusamy等[37 ] 设计了以石蜡和水作为PCM和HTF的低温混合型填充床储热装置,研究表明该装置在间歇性需求的条件下具有更好的放热性能。建立了基于多孔介质方法的一维数学模型,通过数值计算结果得出入口流量比孔隙率对储热性能的影响更大。
Hu等[38 ] 设计了一个名为AquaTube的海水淡化实验装置。在假设局部热非平衡的条件下,建立了连续固相模型对系统进行优化分析。通过实验数据对模型进行验证,并用于进一步的参数分析。研究了不同封装材料、PCM热物性、封装尺寸等因素对系统性能的影响。
Aldoss和Rahman[39 ] 开发了不同的连续固相模型,用于比较单级PCM填充床储热系统和多级PCM填充床储热系统的性能。结果表明,多级PCM设计具有更好的蓄放热性能。然而,填充床内添加3级以上的PCM,系统性能并没有显著提高。
Raul等[40 ] 设计了中温填充床储热装置,以商业级有机材料A164(相变温度168.7 ℃)为PCM,Hytherm 600为HTF,分析了球径和孔隙率对蓄放热性能的影响。王艺斐[41 ] 研究了赤藻糖醇、三元熔盐等物质的物性和蓄放热性能。
图5
有效填充床模型转化示意图
Fig. 5
Schematic diagram of effective packed bed model conversion
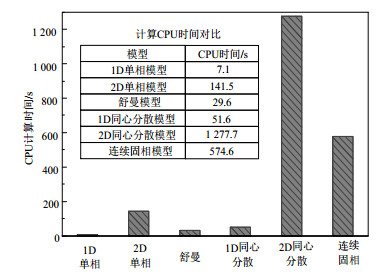
图6
CPU计算时间对比
Fig. 6
Computational cost of each model
[1]
葛志伟 , 叶峰 , MathiruL . 中高温储热材料的研究现状与展望
[J]. 储能科学与技术 , 2012 , 2 (4 ): 89 - 102 .
URL
[本文引用: 1]
[2]
马林 . 导流隔板式相变储热单元性能强化的模拟
[J]. 分布式能源 , 2017 , 2 (3 ): 39 - 44 .
URL
[本文引用: 1]
[3]
Xu J , Wang R Z , Li Y . A review of available technologies for seasonal thermal energy storage
[J]. Solar Energy , 2014 , 103 , 610 - 638 .
[本文引用: 1]
[4]
Sharma A , Tyagi V , Chen C R , et al . Review on thermal energy storage with phase change materials and applications
[J]. Renewable and Sustainable Energy Reviews , 2009 , 13 (2 ): 318 - 345 .
[本文引用: 1]
[5]
Pakrouh R , Hosseini M J , Ranjbar A A , et al . A numerical method for PCM-based pin fin heat sinks optimization
[J]. Energy Conversion Management , 2015 , 103 , 542 - 552 .
[本文引用: 1]
[6]
孙立本 , 张少成 , 许冰 , 等 . 66 kV固体电蓄热装置在火电机组深度调峰中的应用
[J]. 华电技术 , 2018 , 40 (7 ): 38 - 39, 42, 78 .
[7]
李博 , 苑晔 . 槽式太阳能热发电系统数值模拟研究
[J]. 华电技术 , 2018 , 40 (7 ): 14 - 17 .
[8]
左远志 , 杨晓西 , 丁静 , 等 . 熔融盐斜温层蓄热的热特性研究
[J]. 太阳能学报 , 2012 , 33 (1 ): 135 - 140 .
[9]
魏高升 , 邢丽婧 , 杜小泽 , 等 . 太阳能热发电系统相变储热材料选择及研发现状
[J]. 中国电机工程学报 , 2014 , 34 (3 ): 325 - 331 .
URL
[10]
高嵩 . 储热容量对槽式太阳能热发电的影响研究
[J]. 华电技术 , 2016 , 38 (9 ): 71 - 73, 80 .
[本文引用: 1]
[11]
Zhang H , Baeyens J , Caceres G , et al . Thermal energy storage:recent developments and practical aspects
[J]. Proggress in Energy Combust Science , 2016 , 53 , 1 - 40 .
[本文引用: 1]
[12]
赵豫晋 . TICC-500系统储能阶段动态热力特性分析
[J]. 分布式能源 , 2017 , 2 (6 ): 72 - 77 .
URL
[本文引用: 1]
[13]
Wei J , Kawaguchi Y , Hirano S , et al . Study on a PCM heat storage for rapid heat supply
[J]. Applied Thermal Engineering , 2005 , 25 (17 ): 2903 - 2920 .
URL
[本文引用: 1]
[14]
Hawlader M N A , Uddin M S , Zhu H J . Encapsulated phase change materials for thermal energy storage:experiments and simulation
[J]. International Journal of Energy Ressearch , 2002 , 26 (2 ): 159 - 171 .
[本文引用: 1]
[15]
de Gracia A , Cabeza L F . Numerical simulation of a PCM packed bed system:a review
[J]. Renewable and Sustainable Energy Reviews , 2017 , 69 , 1055 - 1063 .
[本文引用: 2]
[16]
Zalba B , Marin J M , Cabeza L F , et al . Review on thermal energy storage with phase change materials, heat transfer analysis and applications
[J]. Applied Thermal Engineering , 2003 , 23 , 251 - 283 .
[本文引用: 1]
[17]
Nagano K , Takeda S , Mochida T , et al . Thermal characteristics of a direct heat exchange system between granules with phase change material and air
[J]. Applied Thermal Engineering , 2004 , 24 , 2131 - 2144 .
[本文引用: 1]
[18]
Schumann T E . Heat transfer:a liquid flowing through a porous prism
[J]. Franklin Inst , 1929 , 208 (3 ): 405 - 416 .
[本文引用: 1]
[19]
Felix R A , Solanki S C , Saini J S . An analysis of a packed bed latent heat thermal energy storage system using PCM capsules:numerical investigation
[J]. Renewable Energy , 2009 , 34 (7 ): 1765 - 1773 .
[本文引用: 1]
[20]
Felix R A, Solanki S C, Saini J S.Thermal performance analysis of phase change material capsules[C]//ISES 2005 Solar World Congress.Orlando, USA, 2005.
[本文引用: 1]
[21]
Tumilowicz E , Chan C L , Li P , et al . An enthalpy formulation for thermocline with encapsulated PCM thermal storage and benchmark solution using the method of characteristics
[J]. International Journal of Heat Mass Transfer , 2014 , 79 , 362 - 77 .
[本文引用: 1]
[22]
左远志 , 杨晓西 , 丁静 , 等 . 操作参数对熔融盐高温斜温层蓄热性能的影响
[J]. 工程热物理学报 , 2012 , 33 (5 ): 868 - 872 .
URL
[本文引用: 1]
[23]
杨小平 , 杨晓西 , 丁静 , 等 . 高温填充床蓄热过程传热特性的实验研究
[J]. 工程热物理学报 , 2014 , 35 (3 ): 529 - 532 .
URL
[24]
尹辉斌 , 丁静 , 杨晓西 . 高温熔融盐斜温层单罐蓄热的热过程特性
[J]. 中国电机工程学报 , 2013 , 33 (26 ): 68 - 74 .
URL
[本文引用: 1]
[25]
Ismail K A R , Henrıquez J R . Numerical and experimental study of spherical capsules packed bed latent heat storage system
[J]. Applied Thermal Engineering , 2002 , 22 (15 ): 1705 - 1716 .
[本文引用: 1]
[26]
Wu M , Xu C , He Y L . Dynamic thermal performance analysis of a molten-salt packed-bed thermal energy storage system using PCM capsules
[J]. Applied Energy , 2014 , 121 (5 ): 184 - 195 .
URL
[本文引用: 1]
[27]
Bédécarrats J P , Castaing-Lasvignottes , Strub F , et al . Study of a phase change energy storage using spherical capsules.Part Ⅱ:numerical modelling
[J]. Energy Conversion Management , 2009 , 50 , 2537 - 2546 .
[本文引用: 1]
[28]
Galione P A , Pérez-Segarra C D , Rodríguez I , et al . A new thermocline-PCM thermal storage concept for CSP plants:numerical analysis and perspectives
[J]. Energy Procedia , 2014 , 49 , 790 - 799 .
[本文引用: 1]
[29]
Yang L , Zhang X S , Xu G Y . Thermal performance of a solar storage packed bed using spherical capsules filled with PCM having different melting points
[J]. Energy and Buildings , 2014 , 68 , 639 - 646 .
[30]
Bindra H , Bueno P , Morris J F , et al . Thermal analysis and exergy evaluation of packed bed thermal storage systems
[J]. Applied Thermal Engineering , 2013 , 52 , 255 - 263 .
[本文引用: 1]
[31]
Panesi A . Numerical and experimental investigation of a fixed bed latent heat storage system during charging processes
[J]. Journal of Mechanical Engineering , 2016 , 14 (1 ): 64 - 72 .
[本文引用: 1]
[32]
Cheng X W , ZHAI X Q , WANG R Z . Thermal performance analysis of a packed bed cold storage unit using composite PCM capsules for high temperature solar cooling application
[J]. Applied Thermal Engineering , 2016 , 100 , 247 - 255 .
[本文引用: 1]
[33]
赵炳晨.熔盐单罐填充床蓄热系统性能分析及优化设计研究[D].北京:中国科学院大学, 2018.
URL
[本文引用: 1]
[34]
Cheralathan M , Velraj R , Renganarayanan S . Heat transfer and parametric studies of an encapsulated phase change material based cool thermal energy storage system
[J]. Journal of Zhejiang University , 2006 , (7 ): 1886 - 1895 .
URL
[本文引用: 1]
[35]
Benmansour A , Hamdan M A , Bengeuddach A . Experimental and numerical investigation of solid particles thermal energy storage unit
[J]. Applied Thermal Engineering , 2006 , 26 , 513 - 518 .
[本文引用: 1]
[36]
Arkar C , Vidrih B , Medved S . Efficiency of free cooling using latent heat storage integrated into the ventilation system of a low energy building
[J]. Interna-tional Journal of Refrigeration , 2007 , 30 , 134 - 143 .
[本文引用: 1]
[37]
Nallusamy N , Sampath S , Velraj R . Experimental investigation on a combined sensible and latent heat storage system integrated with constant/varying(solar) heat sources
[J]. Renewable Energy , 2007 , 32 (7 ): 1206 - 1227 .
[本文引用: 1]
[38]
Hu T , Hassabou A H , Spinnler M , et al . Performance analysis and optimization of direct contact condensation in a PCM fixed bed regenerator
[J]. Desalination , 2011 , 280 , 232 - 243 .
[本文引用: 1]
[39]
Aldoss T K , Rahman M M . Comparison between the single-PCM and multi-PCM thermal energy storage design
[J]. Energy Convers Manag , 2014 , 83 , 79 - 87 .
[本文引用: 1]
[40]
Raul A , Jain M , Gaikwad S , et al . Modelling and experimental study of latent heat thermal energy storage with encapsulated PCMs for solar thermal applications
[J]. Applied Thermal Engineering , 2018 , 143 , 415 - 428 .
[本文引用: 1]
[41]
王艺斐.串联式多相变储热实验与数值模拟研究[D].北京:中国科学院研究生院, 2016.
URL
[本文引用: 1]
[42]
夏莉.复合相变储能材料的研制与潜热储能中热物理现象的研究[D].上海:上海交通大学, 2011.
URL
[本文引用: 1]
[43]
Amin N A M , Belusko M , Bruno F . An effectiveness-NTU model of a packed bed PCM thermal storage system
[J]. Applied Energy , 2014 , 134 , 356 - 362 .
[本文引用: 1]
[44]
Aziz S , Amin N A M , Abdul M M S , et al . Effectiveness-NTU correlation for a TES tank comprising a PCM encapsulated in a sphere with heat transfer enhancement
[J]. Applied Thermal Engineeri-ng , 2018 , 143 , 1003 - 1010 .
[本文引用: 1]
[45]
Ismail K A R , Stuginsky R Jr . A parametric study on possible fixed bed models for pcm and sensible heat storage
[J]. Applied Thermal Engineering , 1999 , 19 , 757 - 788 .
[本文引用: 1]
[46]
Karthikeyan S , Velraj R . Numerical investigation of packed bed storage unit filled with PCM encapsulated spherical containers-a comparison between various mathematical models
[J]. Intertional Journal of Thermal Science , 2012 , 60 , 153 - 160 .
[本文引用: 1]
[47]
Galione P, Lehmkuhl O, Rigola Q, et al.Numerical simulations of thermal energy storage systems with phase change materials[C]//ISES Solar World Congress.Kassel, Germany, 2011.
[本文引用: 1]
[48]
Oró E , Chiu J , Martin V , et al . Comparative stufy of different numerical models of packed bed thermal energy storage systems
[J]. Applied Thermal Engineer-ing , 2013 , 50 , 384 - 392 .
[本文引用: 1]
中高温储热材料的研究现状与展望
1
2012
... id="C3">我国在《可再生能源发展“十三五”规划》中提出了“推动储能技术在可再生能源领域的示范应用,实现储能产业在市场规模、应用领域和核心技术等方面的突破”的发展要求[1 ] .其中,储热技术是储能技术的重要发展方向之一[2 ] ,是太阳能、风能等可再生能源低成本、大规模应用的关键.热能储存(thermal energy storage,TES)按原理可分为显热储热、潜热储热和热化学储热[3 ] .显热储热以其低廉的商业成本成为了传统太阳能热水、太阳能热发电、工业余热回收等系统的主要储热形式,但由于储热密度较低,在大规模应用中对设置环境、设备建造和维护提出了更高的要求[4 ] .潜热储热主要应用相变材料(phase change material,PCM)作为储热介质,具有比显热储热更高的储热密度,在纺织、电子冷却、余热回收、食品储藏、生物医学、供热通风与空气调节以及太阳能热利用[5 -10 ] 等领域应用广泛. ...
导流隔板式相变储热单元性能强化的模拟
1
2017
... id="C3">我国在《可再生能源发展“十三五”规划》中提出了“推动储能技术在可再生能源领域的示范应用,实现储能产业在市场规模、应用领域和核心技术等方面的突破”的发展要求[1 ] .其中,储热技术是储能技术的重要发展方向之一[2 ] ,是太阳能、风能等可再生能源低成本、大规模应用的关键.热能储存(thermal energy storage,TES)按原理可分为显热储热、潜热储热和热化学储热[3 ] .显热储热以其低廉的商业成本成为了传统太阳能热水、太阳能热发电、工业余热回收等系统的主要储热形式,但由于储热密度较低,在大规模应用中对设置环境、设备建造和维护提出了更高的要求[4 ] .潜热储热主要应用相变材料(phase change material,PCM)作为储热介质,具有比显热储热更高的储热密度,在纺织、电子冷却、余热回收、食品储藏、生物医学、供热通风与空气调节以及太阳能热利用[5 -10 ] 等领域应用广泛. ...
A review of available technologies for seasonal thermal energy storage
1
2014
... id="C3">我国在《可再生能源发展“十三五”规划》中提出了“推动储能技术在可再生能源领域的示范应用,实现储能产业在市场规模、应用领域和核心技术等方面的突破”的发展要求[1 ] .其中,储热技术是储能技术的重要发展方向之一[2 ] ,是太阳能、风能等可再生能源低成本、大规模应用的关键.热能储存(thermal energy storage,TES)按原理可分为显热储热、潜热储热和热化学储热[3 ] .显热储热以其低廉的商业成本成为了传统太阳能热水、太阳能热发电、工业余热回收等系统的主要储热形式,但由于储热密度较低,在大规模应用中对设置环境、设备建造和维护提出了更高的要求[4 ] .潜热储热主要应用相变材料(phase change material,PCM)作为储热介质,具有比显热储热更高的储热密度,在纺织、电子冷却、余热回收、食品储藏、生物医学、供热通风与空气调节以及太阳能热利用[5 -10 ] 等领域应用广泛. ...
Review on thermal energy storage with phase change materials and applications
1
2009
... id="C3">我国在《可再生能源发展“十三五”规划》中提出了“推动储能技术在可再生能源领域的示范应用,实现储能产业在市场规模、应用领域和核心技术等方面的突破”的发展要求[1 ] .其中,储热技术是储能技术的重要发展方向之一[2 ] ,是太阳能、风能等可再生能源低成本、大规模应用的关键.热能储存(thermal energy storage,TES)按原理可分为显热储热、潜热储热和热化学储热[3 ] .显热储热以其低廉的商业成本成为了传统太阳能热水、太阳能热发电、工业余热回收等系统的主要储热形式,但由于储热密度较低,在大规模应用中对设置环境、设备建造和维护提出了更高的要求[4 ] .潜热储热主要应用相变材料(phase change material,PCM)作为储热介质,具有比显热储热更高的储热密度,在纺织、电子冷却、余热回收、食品储藏、生物医学、供热通风与空气调节以及太阳能热利用[5 -10 ] 等领域应用广泛. ...
A numerical method for PCM-based pin fin heat sinks optimization
1
2015
... id="C3">我国在《可再生能源发展“十三五”规划》中提出了“推动储能技术在可再生能源领域的示范应用,实现储能产业在市场规模、应用领域和核心技术等方面的突破”的发展要求[1 ] .其中,储热技术是储能技术的重要发展方向之一[2 ] ,是太阳能、风能等可再生能源低成本、大规模应用的关键.热能储存(thermal energy storage,TES)按原理可分为显热储热、潜热储热和热化学储热[3 ] .显热储热以其低廉的商业成本成为了传统太阳能热水、太阳能热发电、工业余热回收等系统的主要储热形式,但由于储热密度较低,在大规模应用中对设置环境、设备建造和维护提出了更高的要求[4 ] .潜热储热主要应用相变材料(phase change material,PCM)作为储热介质,具有比显热储热更高的储热密度,在纺织、电子冷却、余热回收、食品储藏、生物医学、供热通风与空气调节以及太阳能热利用[5 -10 ] 等领域应用广泛. ...
66 kV固体电蓄热装置在火电机组深度调峰中的应用
0
2018
太阳能热发电系统相变储热材料选择及研发现状
0
2014
储热容量对槽式太阳能热发电的影响研究
1
2016
... id="C3">我国在《可再生能源发展“十三五”规划》中提出了“推动储能技术在可再生能源领域的示范应用,实现储能产业在市场规模、应用领域和核心技术等方面的突破”的发展要求[1 ] .其中,储热技术是储能技术的重要发展方向之一[2 ] ,是太阳能、风能等可再生能源低成本、大规模应用的关键.热能储存(thermal energy storage,TES)按原理可分为显热储热、潜热储热和热化学储热[3 ] .显热储热以其低廉的商业成本成为了传统太阳能热水、太阳能热发电、工业余热回收等系统的主要储热形式,但由于储热密度较低,在大规模应用中对设置环境、设备建造和维护提出了更高的要求[4 ] .潜热储热主要应用相变材料(phase change material,PCM)作为储热介质,具有比显热储热更高的储热密度,在纺织、电子冷却、余热回收、食品储藏、生物医学、供热通风与空气调节以及太阳能热利用[5 -10 ] 等领域应用广泛. ...
Thermal energy storage:recent developments and practical aspects
1
2016
... id="C4">PCM在应用过程中也表现出一些不足,例如大多数PCM导热系数较低,影响了在实际应用过程中的蓄放热效率.为了解决该问题,学者们主要提出了2类方法:一是通过封装技术强化蓄热介质与传热介质间的对流换热,二是通过添加高导热材料提高复合材料的有效导热系数[11 ] .目前,常见的PCM封装形式包括宏观封装、微观封装和多孔介质封装[12 ] ,其中宏观封装技术中以壳管式和填充床式研究最为广泛.Wei等[13 ] 对4种不同几何结构的封装形式进行了数值和实验研究,结果表明,球体、圆柱体、板式和壳管式的放热性能依次递减.Hawlader等[14 ] 对填充床潜热储热装置进行了实验和热性能分析,结果表明,球形封装PCM的蓄放热能力相对更高. ...
TICC-500系统储能阶段动态热力特性分析
1
2017
... id="C4">PCM在应用过程中也表现出一些不足,例如大多数PCM导热系数较低,影响了在实际应用过程中的蓄放热效率.为了解决该问题,学者们主要提出了2类方法:一是通过封装技术强化蓄热介质与传热介质间的对流换热,二是通过添加高导热材料提高复合材料的有效导热系数[11 ] .目前,常见的PCM封装形式包括宏观封装、微观封装和多孔介质封装[12 ] ,其中宏观封装技术中以壳管式和填充床式研究最为广泛.Wei等[13 ] 对4种不同几何结构的封装形式进行了数值和实验研究,结果表明,球体、圆柱体、板式和壳管式的放热性能依次递减.Hawlader等[14 ] 对填充床潜热储热装置进行了实验和热性能分析,结果表明,球形封装PCM的蓄放热能力相对更高. ...
Study on a PCM heat storage for rapid heat supply
1
2005
... id="C4">PCM在应用过程中也表现出一些不足,例如大多数PCM导热系数较低,影响了在实际应用过程中的蓄放热效率.为了解决该问题,学者们主要提出了2类方法:一是通过封装技术强化蓄热介质与传热介质间的对流换热,二是通过添加高导热材料提高复合材料的有效导热系数[11 ] .目前,常见的PCM封装形式包括宏观封装、微观封装和多孔介质封装[12 ] ,其中宏观封装技术中以壳管式和填充床式研究最为广泛.Wei等[13 ] 对4种不同几何结构的封装形式进行了数值和实验研究,结果表明,球体、圆柱体、板式和壳管式的放热性能依次递减.Hawlader等[14 ] 对填充床潜热储热装置进行了实验和热性能分析,结果表明,球形封装PCM的蓄放热能力相对更高. ...
Encapsulated phase change materials for thermal energy storage:experiments and simulation
1
2002
... id="C4">PCM在应用过程中也表现出一些不足,例如大多数PCM导热系数较低,影响了在实际应用过程中的蓄放热效率.为了解决该问题,学者们主要提出了2类方法:一是通过封装技术强化蓄热介质与传热介质间的对流换热,二是通过添加高导热材料提高复合材料的有效导热系数[11 ] .目前,常见的PCM封装形式包括宏观封装、微观封装和多孔介质封装[12 ] ,其中宏观封装技术中以壳管式和填充床式研究最为广泛.Wei等[13 ] 对4种不同几何结构的封装形式进行了数值和实验研究,结果表明,球体、圆柱体、板式和壳管式的放热性能依次递减.Hawlader等[14 ] 对填充床潜热储热装置进行了实验和热性能分析,结果表明,球形封装PCM的蓄放热能力相对更高. ...
Numerical simulation of a PCM packed bed system:a review
2
2017
... id="C6">填充床储热的本质为传热流体(heat transfer fluid,HTF)与PCM封装体在储热装置内的固液传热行为.为降低计算成本,研究人员通常在合理的假设条件下,采用简化的数值模型结合经验关联式进行瞬态热性能分析.填充床储热过程的数值模型主要分为单相模型(平衡模型)和两相模型(非平衡模型).两相模型主要包括舒曼模型、同心扩散模型和连续固相模型[15 ] ,填充床储热数值模型分类如图1 所示. ...
... id="C7">单相模型假设HTF和PCM在相同时刻处于热平衡状态,即具有相同的瞬时温度.因此,仅通过一个能量守恒方程即可描述整体换热过程.具体形式[15 ] 为 ...
Review on thermal energy storage with phase change materials, heat transfer analysis and applications
1
2003
... id="C9">式(1)左侧第1项和第2项分别为HTF和PCM能量变化的时间项,第3项为HTF对流项;右侧2项分别为轴向和径向的热传导.根据假设,该模型更适用于分析具有较高导热系数的储热介质.而中低温PCM导热系数普遍较低,绝大多数石蜡、脂肪酸和水合盐的导热系数[16 ] 均小于1 W/(m·K).因此,该模型一般不适用于中低温填充床潜热储热系统.Nagano等[17 ] 采用该模型研究了未进行封装的PCM颗粒与空气直接换热的系统,如图2 所示.由于PCM颗粒尺寸很小,该模型的准确度较高. ...
Thermal characteristics of a direct heat exchange system between granules with phase change material and air
1
2004
... id="C9">式(1)左侧第1项和第2项分别为HTF和PCM能量变化的时间项,第3项为HTF对流项;右侧2项分别为轴向和径向的热传导.根据假设,该模型更适用于分析具有较高导热系数的储热介质.而中低温PCM导热系数普遍较低,绝大多数石蜡、脂肪酸和水合盐的导热系数[16 ] 均小于1 W/(m·K).因此,该模型一般不适用于中低温填充床潜热储热系统.Nagano等[17 ] 采用该模型研究了未进行封装的PCM颗粒与空气直接换热的系统,如图2 所示.由于PCM颗粒尺寸很小,该模型的准确度较高. ...
Heat transfer:a liquid flowing through a porous prism
1
1929
... id="C10">舒曼模型[18 ] 主要用于分析填充床的传热特性.该模型假设为一维传热,忽略了HTF和PCM的径向和轴向导热.分别建立HTF和PCM的能量方程,如式(2)和(3)所示. ...
An analysis of a packed bed latent heat thermal energy storage system using PCM capsules:numerical investigation
1
2009
... id="C13">Felix等[19 -20 ] 利用舒曼模型研究了太阳能热水系统的PBLTES系统热性能.其数值模型在能量方程中定义了总传热系数U 0 ,其中包含对流传热热阻、封装球壳导热热阻以及PCM相变传热热阻.该系数定义为 ...
1
... id="C13">Felix等[19 -20 ] 利用舒曼模型研究了太阳能热水系统的PBLTES系统热性能.其数值模型在能量方程中定义了总传热系数U 0 ,其中包含对流传热热阻、封装球壳导热热阻以及PCM相变传热热阻.该系数定义为 ...
An enthalpy formulation for thermocline with encapsulated PCM thermal storage and benchmark solution using the method of characteristics
1
2014
... id="C15">Tumilowicz等[21 ] 用类似的舒曼修正模型研究了填充床斜温层.利用等效对流传热的方法,并采用特征值的方法来求解方程.结果证明,特征值方法可以高效计算预测填充床斜温层的运行状态. ...
操作参数对熔融盐高温斜温层蓄热性能的影响
1
2012
... id="C16">杨晓西等人[22 -24 ] 模拟分析了熔融盐高温填充床蓄热罐显热蓄热系统传热特性,并分析了各运行参数对系统的影响;结合相变蓄热特性,开发基于舒曼模型的填充床相变蓄热系统模型,研究了相变蓄热系统传热与流动特性及各影响因素对其蓄热性能的影响. ...
高温填充床蓄热过程传热特性的实验研究
0
2014
高温熔融盐斜温层单罐蓄热的热过程特性
1
2013
... id="C16">杨晓西等人[22 -24 ] 模拟分析了熔融盐高温填充床蓄热罐显热蓄热系统传热特性,并分析了各运行参数对系统的影响;结合相变蓄热特性,开发基于舒曼模型的填充床相变蓄热系统模型,研究了相变蓄热系统传热与流动特性及各影响因素对其蓄热性能的影响. ...
Numerical and experimental study of spherical capsules packed bed latent heat storage system
1
2002
... id="C17">该模型由Ismail和Henríquez[25 ] 开发,模型中将填充床储热罐沿轴向分成许多微元层,HTF沿轴向递进流动传热.假设流体的温度是均匀的,并且等于所在层的平均温度.当HTF与PCM封装球存在温差时,考虑了球壳外表面对流传热热阻和球壳厚度的导热热阻,模型中假定球内传热过程为纯热传导.使用有限差分法和移动网格技术进行求解,并使用实验数据验证了模型的有效性.研究了HTF入口温度、质量流量和封装球导热率对蓄放热时间的影响. ...
Dynamic thermal performance analysis of a molten-salt packed-bed thermal energy storage system using PCM capsules
1
2014
... id="C22">Wu等[26 ] 使用修正的二维同心扩散模型研究了封装高温相变材料的填充床蓄热系统,动量方程中引入了填充层孔隙区惯性系数和渗透率.模型中使用有效导热系数考虑球内液相PCM的自然对流,没有考虑环境损失,且认为储热介质的物性参数为定值.分析了填充高温熔盐PCM蓄放热过程的动态性能.研究结果对实际约束条件下高温PBLTES系统的最佳运行和设计参数具有借鉴意义. ...
Study of a phase change energy storage using spherical capsules.Part Ⅱ:numerical modelling
1
2009
... id="C23">Bédécarrats等[27 ] 提出了另一种同心扩散模型.该模型既考虑了周围流体的传热,又考虑了封装PCM内部的过冷现象. ...
A new thermocline-PCM thermal storage concept for CSP plants:numerical analysis and perspectives
1
2014
... id="C24">Galione等[28 ] 利用同心扩散模型,与HTF动量方程相结合,研究了聚光太阳能电厂中相变储热装置“斜温层”热性能,利用Pacheco等的实验数据对模型进行了验证,并得出结论:如果PCM层位于斜温层顶部和底部,则可充当“缓冲层”,使得出口温度接近熔化温度.此外,他们还证明了使用多级PCM可抑制斜温层的退化,提高系统总储热效率. ...
Thermal performance of a solar storage packed bed using spherical capsules filled with PCM having different melting points
0
2014
Thermal analysis and exergy evaluation of packed bed thermal storage systems
1
2013
... id="C26">此外,Bindra等[30 ] 基于同心扩散模型和㶲分析模型,研究了填料床在循环储存和回收过程中的动态热响应.该模型中考虑了环境损失、PCM球内的温度梯度以及HTF和PCM的轴向热传导.研究结果表明,在较高的储热温度条件下,为了获得更高的㶲回收率,需要系统具有较低的潜热或较低的能量密度.然而,即使在高能量密度的显热蓄热系统中,也可以获得较高的㶲回收率,该结论对于新能源电站大规模应用储热技术具有重要意义. ...
Numerical and experimental investigation of a fixed bed latent heat storage system during charging processes
1
2016
... id="C27">Panesi[31 ] 设计了应用于HVAC系统的填充床蓄冷装置.该系统球形封装水与成核剂(相变温度0 ℃)为PCM,乙醇水溶液为HTF,采用有限差分法和移动网格技术进行计算.结果表明,HTF质量流量和入口温度对蓄冷时间的影响最大. ...
Thermal performance analysis of a packed bed cold storage unit using composite PCM capsules for high temperature solar cooling application
1
2016
... id="C28">Cheng等[32 ] 设计了用于太阳能制冷系统中的填充床蓄冷装置.该装置采用了复合相变材料,通过不同条件下的热性能分析发现,随着HTF入口温度由7 ℃升高至12 ℃,平均储热速率、最大储热容量和㶲效率分别下降了73.9%、44.7%和10.4%.进一步研究了串联填充床储冷装置,得出了3~5级为推荐的CTES串联级数. ...
1
... id="C29">赵炳晨[33 ] 基于同心扩散模型、焓方法及有效导热系数法建立了熔盐单罐填充床蓄热系统的一维瞬态传热数学模型,分析了蓄放热循环过程中系统的性能.量化了不完全蓄热效应对蓄热性能的影响,采用控制变量法研究了关键设计参数对4种填充床蓄热系统蓄热性能的影响. ...
Heat transfer and parametric studies of an encapsulated phase change material based cool thermal energy storage system
1
2006
... id="C32">Cheralathan等[34 ] 对基于PCM的蓄冷装置建立了一维连续固相模型并对其进行了实验验证.利用该模型对蓄冷系统性能进行参数分析,研究了空隙率、斯坦顿数、斯蒂芬数和贝克莱数对其性能影响.结果表明,该模型可以有效计算蓄冷系统传热特性. ...
Experimental and numerical investigation of solid particles thermal energy storage unit
1
2006
... id="C33">Benmansour等[35 ] 建立了以空气作为HTF,石蜡作为PCM的二维连续固相模型,并利用有限差分法对控制方程进行求解.通过实验证明了该模型在不同普朗特数下均适用,并可以应用于雷诺数范围较大的蓄放热过程中. ...
Efficiency of free cooling using latent heat storage integrated into the ventilation system of a low energy building
1
2007
... id="C34">Arkar等[36 ] 使用二维连续固相模型研究基于2个填充床潜热储热装置的机械通风系统的性能,并通过实验进行验证.建立了基于储热量、空气流量和PCM物性的温度响应经验方程,并用于TRNSYS模拟中. ...
Experimental investigation on a combined sensible and latent heat storage system integrated with constant/varying(solar) heat sources
1
2007
... id="C35">Nallusamy等[37 ] 设计了以石蜡和水作为PCM和HTF的低温混合型填充床储热装置,研究表明该装置在间歇性需求的条件下具有更好的放热性能.建立了基于多孔介质方法的一维数学模型,通过数值计算结果得出入口流量比孔隙率对储热性能的影响更大. ...
Performance analysis and optimization of direct contact condensation in a PCM fixed bed regenerator
1
2011
... id="C36">Hu等[38 ] 设计了一个名为AquaTube的海水淡化实验装置.在假设局部热非平衡的条件下,建立了连续固相模型对系统进行优化分析.通过实验数据对模型进行验证,并用于进一步的参数分析.研究了不同封装材料、PCM热物性、封装尺寸等因素对系统性能的影响. ...
Comparison between the single-PCM and multi-PCM thermal energy storage design
1
2014
... id="C37">Aldoss和Rahman[39 ] 开发了不同的连续固相模型,用于比较单级PCM填充床储热系统和多级PCM填充床储热系统的性能.结果表明,多级PCM设计具有更好的蓄放热性能.然而,填充床内添加3级以上的PCM,系统性能并没有显著提高. ...
Modelling and experimental study of latent heat thermal energy storage with encapsulated PCMs for solar thermal applications
1
2018
... id="C38">Raul等[40 ] 设计了中温填充床储热装置,以商业级有机材料A164(相变温度168.7 ℃)为PCM,Hytherm 600为HTF,分析了球径和孔隙率对蓄放热性能的影响.王艺斐[41 ] 研究了赤藻糖醇、三元熔盐等物质的物性和蓄放热性能. ...
1
... id="C38">Raul等[40 ] 设计了中温填充床储热装置,以商业级有机材料A164(相变温度168.7 ℃)为PCM,Hytherm 600为HTF,分析了球径和孔隙率对蓄放热性能的影响.王艺斐[41 ] 研究了赤藻糖醇、三元熔盐等物质的物性和蓄放热性能. ...
1
... id="C39">夏莉[42 ] 建立了研究潜热储能床内部流动与换热的有效填充床数学模型,该模型具有很强的通用性,可以反映出储能床内部详细的流动信息和相变单元内部详细的温度梯度,如图5 所示.该模型可以描述出不同填充床中相变小球的排列情况.通过数值模拟研究了储能床中相变小球的堆积方式,以及PCM的封装方式对潜热储能床性能的影响,结果显示:在放热过程中,导热系数较高的不锈钢封装材料可有效减少放热时间且封装材料厚度对系统性能没有显著影响,随机排列布置性能高于规则排列. ...
An effectiveness-NTU model of a packed bed PCM thermal storage system
1
2014
... id="C40">Amin等[43 ] 利用e-NTU方法,建立了一种适用于相变传热预测的半解析二维模型,应用于球形PCM填充床蓄热系统.为了考虑相变过程的变化,采用等温平行路径传热的方法确定热阻,并对模型进行了实验验证.Aziz等[44 ] 提出了利用e-NTU模型对PCM封装球的强化传热过程进行描述.结果表明,系统的热阻是换热效率的重要因素,利用该方法可用于对球形封装的填充床蓄热系统进行优化设计. ...
Effectiveness-NTU correlation for a TES tank comprising a PCM encapsulated in a sphere with heat transfer enhancement
1
2018
... id="C40">Amin等[43 ] 利用e-NTU方法,建立了一种适用于相变传热预测的半解析二维模型,应用于球形PCM填充床蓄热系统.为了考虑相变过程的变化,采用等温平行路径传热的方法确定热阻,并对模型进行了实验验证.Aziz等[44 ] 提出了利用e-NTU模型对PCM封装球的强化传热过程进行描述.结果表明,系统的热阻是换热效率的重要因素,利用该方法可用于对球形封装的填充床蓄热系统进行优化设计. ...
A parametric study on possible fixed bed models for pcm and sensible heat storage
1
1999
... id="C41">Ismail等[45 ] 的研究中针对同一案例对比了4个模型的计算性能,该工作使用相同的计算机记录了4种情况下的CPU计算时间,如图6 所示.结果表明,在一维模型的情况下,计算时间最长的是同心扩散模型,时间最短的是单相模型.使用二维模型计算会导致计算时间大幅度增加,在单相模型和连续固相模型2种情况下,时长增加了约20倍. ...
Numerical investigation of packed bed storage unit filled with PCM encapsulated spherical containers-a comparison between various mathematical models
1
2012
... id="C42">Karthikeyan等[46 ] 将3种模型的数值结果与前期实验的数据进行了对比.其中,分别包括舒曼模型、连续固相模型(考虑了HTF和PCM沿轴向的热传导,但并未考虑径向传导效应)和同心扩散模型.结果表明,同心扩散模型能够更准确地预测系统性能,因为PCM的低导热率会严重影响球体内部的导热. ...
1
... id="C43">此外,Galione等[47 ] 将同心扩散模型与二维CFD模型进行了比较.Oró等[48 ] 比较了基于Brinkmann方程的连续模型和同心扩散模型,Brinkman方程从Darcy模型的转变,可以模拟流动内部的重力,但不能考虑PCM球体内部的温度梯度,与实验数据的比较验证了模型的有效性. ...
Comparative stufy of different numerical models of packed bed thermal energy storage systems
1
2013
... id="C43">此外,Galione等[47 ] 将同心扩散模型与二维CFD模型进行了比较.Oró等[48 ] 比较了基于Brinkmann方程的连续模型和同心扩散模型,Brinkman方程从Darcy模型的转变,可以模拟流动内部的重力,但不能考虑PCM球体内部的温度梯度,与实验数据的比较验证了模型的有效性. ...