能源是社会发展和经济增长最基本的驱动力，是人类赖以生存的基础^[1-2]。风能是一种清洁、取之不尽、用之不竭的可持续利用的资源，在当前化石能源面临枯竭和生态环境严重污染的情况下，风能的高效开发利用已成为我国乃至世界能源开发的一大热点^[3-4]，同时人们在日常生产和生活中所需能源的主要形式为热能。风能制热研究在世界能源紧缺的今天具有十分重要的意义。

传统的制热方法是通过风能转化为电能，然后通过焦耳效应将电能转化为热能^[5]。而在这种双转换过程中需要复杂且昂贵的电子设备，同时风能的利用率不是很高^[6-9]。现阶段，风力直接制热方式大体可分为4种：液体搅拌制热、液体挤压制热、固体摩擦制热和磁涡流制热^[10]。永磁涡流制热的机制是通过风力机带动制热装置转子旋转产生变化磁场，根据法拉第电磁感应定律，金属定子受到变化磁场的影响产生电涡流继而使金属定子生成热并加热定子水槽内的水，将风力机的机械能转换为热能，并通过水槽内的水将热量供给热力系统。

鉴于我国东北地区风能资源丰富，而且东北地区弃风问题严重^[11-12]。因此高效的永磁涡流风力制热装置，有利于利用冬季充足的风能对外供热，是提高风能利用率的有效途径。同时，也有利于缓解我国煤炭资源紧张的局面并有益于缓解我国现阶段的环境污染等问题。

目前在风力制热方面主要以试验研究和数值模拟为主，对制热装置参数设计方面的研究还比较少^[13-15]。本文运用风力机输出功率相关公式及涡流制热原理，对制热装置定子内墙的长度与内径的关系进行研究。并在此基础上，确定磁极对数、永磁体厚度和气隙长度等参数，为垂直轴风力机永磁涡流制热装置的设计提供了理论依据。

垂直轴风力机具有结构简单、制造工艺易行、无须偏航设置、安装方便、经济实用的特点^[16]。相对于水平轴风力机还具有运行噪音小、变速装置和永磁涡流制热装置便于放置等优点。风力机获得的机械能取决于风速和风力机的机构参数，风力机风轮输出功率为

(1) $P = 1/2{C_{\rm{P}}}\rho A{V^3}$

式中：C_P为风能利用系数；r为空气密度，kg/m³；A为风轮扫掠面积，m²；V为额定风速，m/s。

垂直轴风力机叶片扫掠面积：

(2) $A = 2hR$

式中：h为风轮高度，m；R为风轮的旋转半径，m。

根据风力机的转矩M与风力机功率P的关系可知，垂直轴风力机的转矩：

(3) $M = \frac{P}{{{\omega _{\rm{a}}}}} = \frac{{{C_{\rm{P}}}\rho A{V^3}}}{{2{\omega _{\rm{a}}}}}$

式中${\omega _{\rm{a}}}$为风机转速，r/min。

风能利用系数C_P为叶尖速比λ的函数^[16]，如图1所示。

(4) $\lambda = \frac{{R{\omega _{\rm{a}}}}}{V}$

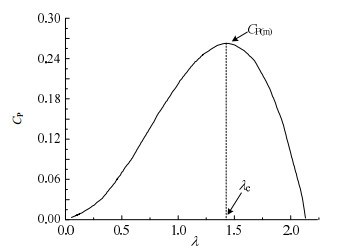
由于C_P非线性且有最大值C_P(m)，此时λ所对应的值为λ_e，如图1所示。将式(4)中的V代入式(3)得

(5) ${M_{\rm{t}}} = \frac{{{C_{\rm{P}}}\rho A{R^3}}}{{2{\lambda ^3}}}{\omega _{\rm{a}}}^2$

因此，根据图1的对应关系，当λ为λ_e时，C_P为最大值C_P(m)时的转矩：

(6) ${M_{\rm{G}}} = \frac{{{C_{{\rm{P(m)}}}}\rho A{R^3}}}{{2{\lambda _{\rm{e}}}^3}}{\omega _{\rm{a}}}^2$

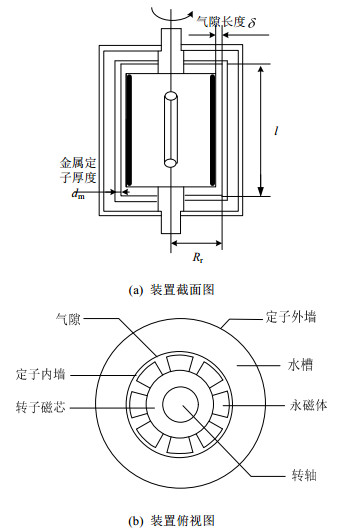
涡流制热试验装置2D切面模型如图2所示。当永磁涡流制热装置转子旋转时在金属定子内产生感应电流，根据电磁感应定律：

(7) $e = {B_x}{l_{\rm{a}}}v$

式中：e为导体感应电动势，V；l_a为导体处于磁场中的有效长度，m；B_x为导体所切割的气隙磁通密度，T；v为导体与磁场的相对速度，m/s。

导体感应电动势e正比于导体所切割的气隙磁通密度B_x，也就是说，导体感应电动势的波形正比于制热装置气隙内磁通密度沿气隙分布的波形。如要得到正弦波形的电动势，就必须使气隙磁通密度沿气隙分布的波形为正弦波形。

气隙磁通密度B_x的分布曲线关系式为

(8) ${B_x} = {B_{\rm{m}}}\sin \frac{{\rm{ \mathit{ π} }}}{\tau }x$

式中：x为气隙中某一点与磁极中性线的距离，m；τ为转子中相邻N极与S极间的距离，m；B_m为气隙磁通密度的最大值，T。

气隙中某一点与磁极中性线的距离用电角表示为$\frac{{\rm{ \mathit{ π} }}}{\tau }x$，在此正弦波磁场作用下的导体电动势为

(9) ${e_{\rm{c}}} = {B_m}{l_{\rm{a}}}v\sin \frac{{\rm{ \mathit{ π} }}}{\tau }x$

而速度$v$可以表示为：

(10) $v = \frac{{2p\tau n}}{{60}} = 2\tau f$

(11) $x = vt$

式中：p为永磁转子极对数；n为转子转速，r/min；f为电动势的频率，Hz；t为时间，s。

联立式(10)和式(11)，气隙中某一点与磁极中性线的距离用电角表示为

(12) $\frac{{\rm{ \mathit{ π} }}}{\tau }x = \frac{{\rm{ \mathit{ π} }}}{\tau }\nu t =-\frac{{\rm{ \mathit{ π} }}}{\tau }2\tau ft = \omega t$

式中ω为永磁转子角速度，rad/s。因此，式(9)可以表示为

(13) ${e_{\rm{c}}} = {B_{\rm{m}}}{l_{\rm{a}}}\nu \sin \omega t = E_{{\rm{cm}}}^{}\sin \omega t$

这说明，磁通密度沿气隙分布为正弦波时，导体感应电动势的波形也为正弦函数。式(13)中${E_{{\rm{cm}}}} = {B_{\rm{m}}}{l_{\rm{a}}}\nu $为导体电动势的最大值。

因此，导体电动势的有效值为

(14) ${E_{\rm{c}}} = \frac{{{E_{{\rm{cm}}}}}}{{\sqrt 2 }} = \frac{{B_{\rm{m}}^{}{l_{\rm{a}}}\nu }}{{\sqrt 2 }} = \frac{{B_{\rm{m}}^{}{l_{\rm{a}}}2\tau f}}{{\sqrt 2 }}$

气隙磁通密度的最大值还可表示为

(15) ${B_{\rm{m}}} = \frac{{\rm{ \mathit{ π} }}}{2}{B_{\rm{a}}}$

式中B_a为磁通密度的平均值，T。

考虑到每极磁通：

(16) ${\mathit{\Phi} _{\rm{a}}} = {B_{\rm{a}}}{l_a}\tau $

式中Φ_a为每极磁通，Wb。

由于磁通密度为正弦波，联合式(14)—(16)可知导体电动势还可表示为

(17) ${E_{\rm{c}}} = 2.22f{\mathit{\Phi} _{\rm{a}}}$

可见，每根导体电动势的有效值大小与每极磁通量和电动势的频率成正比。对于整个金属定子电动势E相当于若干个导体电动势E_c之和，即

(18) $E = \sum {{E_{\rm{c}}}} = 2.22f{\mathit{\Phi} _{\rm{a}}}\oint\limits_L {{\rm{d}}s = 4.44{\rm{ \mathit{ π} }}{R_{\rm{r}}}} f{\mathit{\Phi} _{\rm{a}}}$

式中R_r为定子内墙半径，m。

金属定子的阻抗Z可以表示为

(19) $ Z = \sqrt {{R_{\rm{L}}}^{\rm{2}} + {X_{\rm{L}}}^{\rm{2}}} $

式中：R_L为金属电阻，Ω；X_L为金属感抗，Ω。其中：

(20) $\left\{ \begin{array}{l}{R_{\rm{L}}} = \frac{{{\rho _{\rm{l}}}l}}{S}\\{X_{\rm{L}}} = 2{\rm{ \mathit{ π} }}Lf = \omega l\end{array} \right.$

式中：ρ_l为金属电阻率，Ω·m；l为金属导体长度，m；S为导体横截面积，m²；L为金属电感，H。

通过联立式(19)和(20)可知金属导体的阻抗：

(21) $Z = \sqrt {\frac{{{\rho _{\rm{l}}}^2{l^2}}}{{{S^2}}} + {\omega ^2}{L^2}} $

感应涡流在金属导体中所产生的功率为

(22) $P = \frac{{{E^2}}}{Z}$

将式(18)和式(21)代入式(22)可知感应涡流在金属导体中所产生的功率可表示为

(23) $P = \frac{{{{(4.44{\rm{ \mathit{ π} }}{R_{\rm{r}}}f{\Phi _2})}^2}S}}{{\sqrt {{\rho _{\rm{l}}}^2{l^2} + {{(\omega LS)}^2}} }}$

由于铁磁导体会受到趋肤效应的影响，其趋肤深度为

(24) $d = \sqrt {\frac{2}{{\omega \mu \gamma }}} $

式中：μ为金属磁导率，H/m；γ为金属电导率，S/m。

而根据永磁涡流制热装置原理，定子内墙须使用矫顽力H_c要小，相对磁导率μ_γ要大的软磁材料，比如碳钢。碳钢的磁导率一般在5 000~7 000 S/m左右，所以根据式(24)计算，其趋肤深度最大不超过5 mm，因此取金属定子厚度d_m为5 mm。所以定子内墙的外径可用(R_r+0.005)表示，即定子内墙的截面积S可表示为

(25) $S = {\rm{ \mathit{ π} [(}}{R_{\rm{r}}} + 0.005{{\rm{)}}^2}-{R_{\rm{r}}}^2{\rm{]}}$

将其代入式(23)可知感应涡流在金属导体中所产生的功率还可表示为

(26) $P = \frac{{{{(4.44{\rm{ \mathit{ π} }}{R_{\rm{r}}}f{\Phi _{\rm{a}}})}^2}{\rm{ \mathit{ π} [}}{{({R_{\rm{r}}} + 0.005)}^2}-{R_{\rm{r}}}^2{\rm{]}}}}{{\sqrt {{\rho _{\rm{l}}}^2{l^2} + {\omega ^2}{L^2}{{\rm{ \mathit{ π} }}^2}{{[{{({R_{\rm{r}}} + 0.005)}^2}-{R_{\rm{r}}}^2]}^2}} }}$

永磁涡流制热装置的转矩为

(27) ${T_{\rm{G}}} = \frac{P}{\omega } = \frac{{{{(4.44{\rm{ \mathit{ π} }}{R_{\rm{r}}}f{\Phi _{\rm{a}}})}^2}{\rm{ \mathit{ π} [}}{{({R_{\rm{r}}} + 0.005)}^2}-{R_{\rm{r}}}^2{\rm{]}}}}{{\omega \sqrt {{\rho _{\rm{l}}}^2{l^2} + {\omega ^2}{L^2}{{\rm{ \mathit{ π} }}^2}{{[{{({R_{\rm{r}}} + 0.005)}^2}-{R_{\rm{r}}}^2]}^2}} }}$

联合式(26)和式(27)，当永磁涡流制热装置与风力机匹配时M_G=T_G，即

(28) $\begin{array}{l}\frac{{{C_{{\rm{P}}({\rm{m}})}}\rho A{R^3}}}{{2{\lambda _{\rm{e}}}^3}}{\omega _{\rm{a}}}^2 = \\{\rm{ }}\frac{{{{(4.44{\rm{ \mathit{ π} }}{R_{\rm{r}}}f{\Phi _{\rm{a}}})}^2}{\rm{ \mathit{ π} [}}{{({R_{\rm{r}}} + 0.005)}^2}-{R_{\rm{r}}}^2{\rm{]}}}}{{\omega \sqrt {{\rho _{\rm{l}}}^2{l^2} + {\omega ^2}{L^2}{{\rm{ \mathit{ π} }}^2}{{[{{({R_{\rm{r}}} + 0.005)}^2}-{R_{\rm{r}}}^2]}^2}} }}\end{array}$

因此，可知定子内径R_r与长度l的关系为

(29) $\begin{array}{l}l = \frac{{\sqrt {4{\lambda _{\rm{e}}}^6{{(4.44{\rm{ \mathit{ π} }}R{}_rf{\Phi _{\rm{a}}})}^4}- {C_{{\rm{P}}({\rm{m}})}}\rho A{R^3}{\omega _{\rm{a}}}^2{\omega ^4}{L^2}} }}{{{C_{{\rm{P}}({\rm{m}})}}\rho A{R^3}{\omega _{\rm{a}}}^2\omega {\rho _{\rm{l}}}}} \cdot \\{\rm{ \mathit{ π} [}}{({R_{\rm{r}}} + 0.005)^2}-{R_{\rm{r}}}^2{\rm{]}}\end{array}$

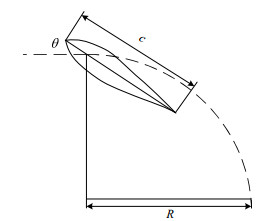
选用NACA0024作为风力机的叶片，风力机的叶片数n=4，弦长c=0.15 m，风力机叶片的旋转半径R=0.4 m，叶片高度H=0.8 m，安装角度θ=10°，垂直轴风力机相关参数如图3所示。

根据已有研究可知，永磁体的厚度为4~16 mm的磁场幅值随着厚度的增加而增大，同时考虑工程实际和其他因素，本课题拟采用永磁体的厚度为5 mm。通过比较不同极对数下制热装置的磁感线分布、磁感应强度分布、气隙磁通密度曲线及输入转矩与时间的关系，最终确定磁极对数为2p=20。由于装置运行时感应电动势无变化，因此考虑装置中无自感现象。以垂直轴风力机为例，假设风速V=8 m/s，ω_a=26 rad/s，将下列参数：$A = 2hR = 2 \times 0.8 \times 0.4 = 0.64{{\rm{m}}^2}, g = 9.8{\rm{m}}/{{\rm{s}}^2}, $${\rho _{\rm{A}}} = {\rm{ }}1.225{\rm{kg}}/{{\rm{m}}^3}, {C_{{\rm{P(m)}}}} = 0.25, R = 0.4{\rm{m}}, $$f = 50{\rm{Hz, }}{\lambda _{\rm{e}}} = 1.3, $${\rm{ }}{\rho _{\rm{l}}} = 5 \times {10^{ - 5}}\Omega \cdot {\rm{m, }}l = 0.5{\rm{m}}{\rm{。}}$代入式(29)得到：

(30) $\begin{array}{l}0.5 = \frac{{2 \times {{1.3}^3} \times {{4.44}^2} \times {{1.16}^2} \times {{0.5}^2} \times {{\rm{ \mathit{ π} }}^4}R_{\rm{r}}^2}}{{0.25 \times 1.225 \times 0.64 \times {{0.4}^3} \times {{26}^2} \times 100 \times 5 \times {{10}^{-5}}}} \cdot \\{\rm{ }}(0.01{R_{\rm{r}}} + {0.005^2}){\rm{ }}\end{array}$

求解得R_r=0.084 8 m。

根据气隙长度δ的经验公式

(31) $\delta = 0.3(0.4 + 7\sqrt {2{R_{\rm{r}}}l} ) \times {10^{-3}}$

由式(30)计算得到气隙长度δ=0.74 mm。考虑到制热转子在实际运行中有可能发生振动、偏移等现象，根据实际考虑气隙不宜太小，因此本课题最终拟定气隙长度δ=1 mm。根据上述研究结果可知永磁涡流制热装置的参数见表1。

通过建立数学模型，为垂直轴风力机永磁涡流制热装置的设计提供了理论依据。在设计过程中，首先根据需要的热量确定风力机的功率，然后根据数学模型确定制热装置定子内墙的长度与内径的关系，根据涡流制热的原理确定磁极对数、永磁体厚度和气隙长度等其他参数。由此设计出所需容量的风力制热装置。