人工智能是一门研究用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的新的技术科学，该领域的研究包括机器人、语言识别、图像识别、自然语言处理和专家系统等。2016年1月27日，期刊《自然》封面文章报道，谷歌开发的名为“阿尔法围棋”(Alpha Go)的人工智能机器人以5:0完胜欧洲围棋冠军樊麾。2016年3月，Alpha Go挑战世界围棋冠军李世石，最终以4比1的总比分取得了胜利。2017年5月，它以3比0战胜曾获多项国内和国际围棋大赛冠军的中国围棋当今名将柯洁。AlphaGo用到了很多新技术，如深度神经网络和蒙特卡洛树搜索法等，是人工智能理论和应用研究发展到新阶段的产物。AlphaGo的上乘表现使得人工智能引起了社会各界的极大关注。2016年10月，美国国家科学技术委员会发布了《国家人工智能研发战略规划》。2017年7月，我国国务院发布了《新一代人工智能发展规划》。

人工智能在电力系统中的应用在20世纪80年代至21世纪初备受关注。1988年，在瑞典的斯德哥尔摩召开了第一届专家系统在电力系统中的应用的研讨会之后，至今适逢30周年。这种研讨会每一至两年召开一次，并且随着人工神经网络研究的升温，研讨会的名字改为了“智能系统在电力系统中的应用”。国际大电网会议(CIGRE)已多次有组织地对专家系统在电力系统中的应用状况进行过调查，并在1992年会议上将其列为优先讨论课题。然而，开发专家系统存在获取专家知识困难和建造周期长的问题，神经网络又存在所需要的大量样本难以获取且学习过程的参数调优缺乏依据和培训复杂等困难，智能系统的研发和应用都遇到了巨大的挑战。目前，随着计算机计算能力的提高，大数据的不断积累，国家政策的积极扶持，人工智能在电力系统中的应用研究又面临新机遇。

本文旨在总结人工智能在电力系统中的应用研究和实践工作，为新涉足这一研究领域的研究工作者提供参考。重点介绍21世纪初出现的基于有限样本训练的相关向量机的特点、原理及其在电力系统中的应用。

专家系统是在一个狭窄的领域内，利用专家经验来解决复杂问题的智能软件。20世纪80年代和90年代上半期，专家系统在电力系统中的应用研究如火如荼，涉及电力系统报警处理、故障诊断、运行规划、控制和系统分析等，采用的知识表示方法以产生式规则为主，也有一阶谓词逻辑、框架和语义网^[1]等，后期的应用研究大都采用Prolog或C++，故一阶谓词逻辑和面向对象知识表示方法成为主流。由于Prolog拥有内部自动推理机制、内嵌的数据库管理和通用的一阶谓词知识表示方法，所以即使在现在也是实现演绎推理的一个良好语言和工具。

我国开展专家系统在电力系统中的应用研究在国际上不算晚。首例是华北电力学院杨以涵教授指导的研究生张志英在1985年所研发的用于电力系统日调度计划的专家系统^[1-2]，目标是运用专家经验确定机炉启停计划，当时是在PDP机上用LISP语言实现的，系统的编排结果基本上能得到调度员的认可，但软件的汉化问题未解决，故研发的系统未得到实际应用。

笔者在杨以涵教授的指导下，于1986年研发了用于变电站操作票编写的专家系统^[3]，该系统属于产生式系统，从操作任务和已知运行方式为依据，利用专家经验进行扩展推理。这一课题的研究始于1985年底，并于1986年底在铁岭一次变电所投人运行，这是国内电力系统中第一个实际投入运行的专家系统。由于当时智能语言Prolog和LISP的汉化问题没有解决，所以这一系统只好用BASIC编写，使得在程序的通用性受到了限制，但对研究工作起了很大的推动作用。

杨以涵教授带领课题组开展了火电站的倒闸操作票和高压开关诊断专家系统。从1989年春，杨以涵教授为东北电网研发了电网操作票、故障分析和处理专家系统。由于使用Prolog表示电网拓扑结构和专家知识很便利，且能实现内部自动推理，故课题组决定采用Prolog进行系统的研发。电网操作票的用量大，但种类较少，特别适合用Prolog和专家系统来解决。笔者所在团队开发的系统^[4]在当时东北电网总调度应用3年以上，开票使用率达97%左右，缩短了调度编写操作票的时间^[5]。电网故障诊断和处理专家系统要复杂得多，当时EMS的信息较少，直接可用的就是开关的状态和跳闸信息，最后我们提出了以开关跳闸分布为主，保护动作情况提问为辅的诊断方法^[6]，在VAX机上用GKD Prolog实现了该专家系统^[7]，获得了电力工业部科技理论成果二等奖。由于受当时计算机应用水平的限制，系统界面比较粗燥，同EMS的信息交换也不顺畅，应用效果大打折扣，但验证了理论上是可行的。

在20世纪80年代末和90年代初，多家单位都开展了专家系统应用的研究^[1]，如：上海交大的配电网操作票系统及无功控制系统，浙江大学的紧急控制、华中理工大学的无功控制、福州大学的配电网经济运行系统。出自企业的有江西中调所的负荷预测和黑龙江省调的无功优化系统；出自科研单位的有原南京自动化所的动态安全运行规划决策支持系统和警报压缩处理系统。此外，中国电力科学研究院、西安交通大学及东南大学等单位也在开展这方面的工作。

神经网络在电力系统中的应用主要是BP神经网络的出现之后。BP神经网络可实现任意复杂的非线性关系映射，对大量的训练样本进行拟合，而任何具体的判别函数都做不到这一点，因而BP模型的分类和预测结果要比常规的模式识别法都要好。它特别适合有大量结论性(标签)样本而又缺乏显式专家规则的场合，如图像和声音识别，且具有对于错误样本的容错能力，因而对于很多模式识别问题的应用都取得了成功。在电力系统中的应用研究主要涉及负荷预测、电力系统的动态安全估计、电力设备和输电线路的故障诊断。但是由于神经网络需要大量的培训样本，输入输出的变化越多，需要的培训样本数量越大，在解决很多故障诊断问题方面会遇到取得大量训练样本难的问题，因而BP神经网络在电力系统中的成功应用并不很多。

进化计算的方法较多，如遗传算法、粒子群优化算法、蚁群算法和进化规化等，但本质上都是优胜劣汰，迭代求优，适合于非线性优化问题的求解。电力系统的优化问题主要有：电网结构规划(包括线路增设)、电网调度中的机组起停优化、机组检修计划优化、电网运行无功优化(包括电容器投切和变压器分接头的调节)等，大多属于大规模的非线性或动态规划问题，适合用进化计算方法来解决，而用传统的非线性优化和动态规划法是无法解决的，如传统的动态规划法对于大规模的动态规划问题会出现组合爆炸问题。进化计算在电力系统中的应用相对要成功一些。

由于人工神经元网络需要的样本多，培训时间长等问题，故自21世纪初，人工智能在电力系统中的应用研究又转向支持有限样本学习的支持向量机和相关向量机。

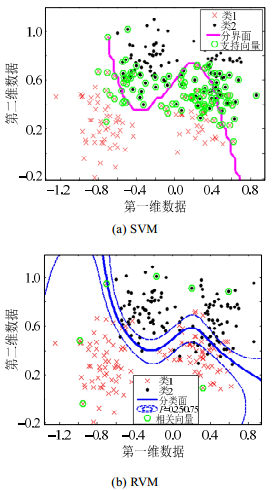
相关向量机(relevance vector machine，RVM)是Micnacl E. Tipping于2001年在稀疏贝叶斯学习理论基础上提出的一种监督学习算法，该方法结合了贝叶斯理论、马尔科夫性质、最大似然估计以及自动相关决定(automatic relevance determination，ARD)等理论^[8-10]。RVM的函数形式与支持向量机(support vector machine，SVM)类似，同样是基于核函数映射将低维空间非线性问题转化为高维空间的线性问题，都可有效地解决小样本、高维、非线性分类问题。但RVM还具有以下优势^[8-10]：1）RVM核函数不受Mercer条件的限制，核函数的选取范围更广；2）无规则化系数，不需要通过交叉验证等方法获取该参数；3）泛化能力更好；4）基函数权值只有少数非零，相关向量数量少，模型更稀疏；5）测试时间(诊断速度)更快，更适合在线诊断；6）可以给出概率输出，便于分析问题的不确定性。相关向量机主要是用于解决二分类问题^[8-10]，对于多分类问题通常需要采用“一对多”、或“二叉树”等方法，将其转化为多个二分类问题，但这些方法存在分类重叠和不可分类、需要构建较多分类器等问题。然而实际中存在许多分类问题，针对此Damoulasy等人对二分类相关向量机进行了扩展，提出了多分类相关向量机(milticlass relevance vector machine，M-RVM)以及组合核相关向量机(multi-kernel learning relevance vector machine，MKL-RVM)，二者通过引入多项概率似然函数，采用分层贝叶斯模型结构，直接实现多分类。同时MKL-RVM通过组合核的形式，实现了非同构的多信息数据的信息融合^[11-14]。RVM已广泛应用于分类、预测等领域，并在电力系统的分类、预测等领域取得了很好的应用效果^[15-22]。

二分类RVM基于核函数映射将低维空间非线性问题转化为高维空间的线性问题，有效解决小样本、高维、非线性分类问题。不同于SVM基于结构风险最小化原则构建学习机，RVM是基于贝叶斯框架构建学习机，因此RVM不仅获得二值输出，而且获得概率输出。对于给定的训练样本集$\{ {x_n}, {t_n}\} _{n-1}^N$，RVM的学习模型为$y(\mathit{\boldsymbol{x}};\mathit{\boldsymbol{w}}) = \sum\limits_{i = {\rm{1}}}^N {{\omega _i}K(\mathit{\boldsymbol{x}};{\mathit{\boldsymbol{x}}_i}) + {\omega _0}} $，其中$\mathit{\boldsymbol{w}} = {[{w_0}, {w_1}, {w_2}, \ldots, {w_N}]^{\rm{T}}}$为权重向量，${\omega _i}$为权重，$K(\mathit{\boldsymbol{x}};{\mathit{\boldsymbol{x}}_i})$为核函数。为避免采用最大似然估计(maximum likelihood)方法求解存在的过拟合问题，RVM对权重向赋予零均值Gaussian先验分布，把对权重的求解转化为对超参数的求解，求解的过程中大部分超参数接近无限大，其对应的权重为0，从而确保模型的稀疏性。而其它的超参数则会稳定于有限值，与之对应的${\mathit{\boldsymbol{x}}_i}$就称之为相关向量，同时在超参数估计的过程中自动调节规则化系数，从而不需要对规则化系数进行验证。

图1(a)和图1(b)分别给出了SVM和RVM方法对Ripley给出的典型分类数据集synthetic的分类输出，可以看出相关向量的数量明显少于支持向量，并且RVM可以输出概率分布情况。

将相关向量机用于变压器故障诊断^[15]，采用二叉树分类方法，将多分类问题转化为多个二分类问题。采用归一化的H₂、CH₄、C₂H₆、C₂H₄、C₂H₂五种特征气体含量作为RVM分类器的输入，用4个RVM分类器来辨识变压器正常、低能放电、高能放电、中低温过热、高温过热5种状态。实例分析表明该方法可以取得与SVM相当甚至是更优诊断正确率，故障诊断速度更快。

文献[16]提出了基于振动信号样本熵和相关向量机的万能式断路器分合闸故障诊断方法，该方法以分合闸动作过程中各频带样本熵特征向量作为RVM的输入，以万能式断路器正常、虚假合闸、分闸不彻底或某相不同期的机械状态为RVM的输出。所提方法可利用相对较少的故障数据样本实现对万能式断路器故障类型的识别并具有较高的识别率。

文献[17]提出了电力系统静态安全状态实时感知的相关向量机法，该方法首先根据日前市场的运行与调度规则，产生运行条件，构造安全评估特征集及事故安全分类；然后将Relief算法用于发电机出力、节点负荷、支路潮流等故障前稳态特征值的特征排序，筛选出与分类紧密相关的特征子集，作为RVM的输入。

RVM贝叶斯框架下的ARD先验分布设置确保了RVM模型的稀疏性，仅极少数相关向量参与在线安全决策，有效克服了过度拟合问题，分类准确度高；同时少量核函数运算使决策时间缩短。RVM模型的概率输出不仅能够提供分类信息，还可用于系统的风险管理，为系统风险评估、风险决策提供支持。

多分类相关向量机(multiclass relevance vector machine，M-RVM)是Damoulasy等人于2008在二分类核函数学习、高斯过程组合协方差函数方法以及高斯先验处理多项概率似然函数方法的基础上，提出的一种基于贝叶斯框架的统计学习算法^[11]。

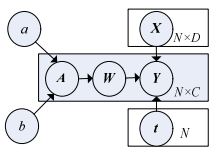
M-RVM采用分层贝叶斯模型结构，通过引入多项概率似然函数(multinomial probit likelihood)，实现了多分类和输出类别成员概率。设训练集$\mathit{\boldsymbol{X}} = \{ {\mathit{\boldsymbol{x}}_i}, {t_i}\} _{i = 1}^N$，$\mathit{\boldsymbol{x}} \in {R^D}$，${t_i} \in \{ 1, \ldots, C\} $为类别标签，引入辅助回归目标Y$ \in $R^CxN和权重参数W$ \in $ R^NxC，先验参数${\alpha _{nc}}$组成的矩阵记为$\mathit{\boldsymbol{A}} \in {R^{N \times C}}$, ${\alpha _{nc}}$服从超参数为$a$，$b$的Gamma分布。M-RVM的分层贝叶斯模型结构示意图如图2所示。

鉴于变压器故障诊断本质为多分类问题，提出了基于M-RVM的变压器故障诊断方法^[18]，实现了变压器正常、低能放电、高能放电、中低温过热、高温过热、局部放电六种状态的直接分类，而无需将多分类转换为多个二分类的问题。M-RVM诊断输出是变压器处于上述6种状态的概率，可以为变压器的检修提供更多的可用信息。

文献[19]将M-RVM应用于GIS局部放电模式识别中，作者通过试验建立了相应的超高频信号图谱数据库，然后根据信号特点提取了26个原始特征量；采用主成分分析法对特征空间进行降维处理，最终得到10个新的特征量，将原始特征量和降维后的特征量分别输入到多分类相关向量机(M-RVM)中进行分析，结果表明，以降维后的特征量作为输入量，其识别率要高于降维前的；并且同BN和SVM分类器相比，无论是采用原始特征参量还是降维后的参量作为输入量，M-RVM方法的识别率都是最高，其中降维后的识别率大于85%。

文献[20]将M-RVM应用于有轨电车用燃料电池系统故障诊断中，实现了氢气泄漏、去离子水加湿泵低压、空气压力过低和正常共4种状态的快速识别，准确率可达96.67%。

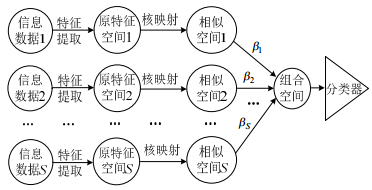
组合核相关向量机(multi-kernel learning relevance vector machine，MKL-RVM)同样采用分层贝叶斯模型结构，通过引入多项概率似然函数(multinomial probit likelihood)，采用组合核的形式实现了非同构的多信息数据或多特征信息的有机融合以及多分类问题。MKL-RVM原理示意图如图3所示，图中S为信息数据的种类，${\beta _1}$, ${\beta _2}, \cdots, {\beta _S}$为组合核参数。

MKL-RVM虽然不存在规则化系数确定困难的问题，核组合参数也可在模型学习的过程自动优化，但核函数参数没有采用自动相关学习算法，需要事先人为设定。MKL-RVM既可以实现单个检/监手段的检/监测数据提取的多组特征信息的融合，还可以实现由多种检/监手段的检/监测数据源提取的非同构特征信息的融合^[12-14]。

文献[21]提出了基于MKL-RVM的电力变压器故障诊断方法。可有效利用蕴含变压器运行状态的多种特征信息；可直接输出变压器为各种状态的概率，为变压器的检修提供更多的可用信息。

文献[22]提出了基于MKL-RVM的变压器局部放电模式识别方法，提出的局部放电特征向量作为MKL-RVM输入，悬浮放电、针板放电、沿面放电和气隙放电四种类型作为输出，建立变压器局部放电模式识别模型。实验结果表明MKL-RVM分类器识别精度较高。

专家系统存在获取专家知识困难和建造周期长的问题，在电力系统中的应用研究主要涉及电力系统报警处理、故障诊断、运行规划、控制和系统分析等。神经网络适用于有大量培训样本而又缺乏显式专家规则的场合，存在参数调优缺乏依据和培训复杂等问题；在电力系统中的应用研究主要涉及负荷预测、电力系统的动态安全估计、电力设备和输电线路的故障诊断。进化计算适用于非线性或动态规划问题，可解决传统动态规划法的组合爆炸问题；在电力系统中的应用研究主要涉及电网结构规划、电网调度中的机组起停优化、机组检修计划优化、电网运行无功优。相关向量机具有需要培训样本数量少，可以输出类别成员概率的优点，适合于样本数据获取困难的预测和分类问题；在电力系统中的应用研究主要涉及负荷预测和电力设备故障诊断。